Over the past few months or so, I have been brushing up on my Lie group theory, as part of my project to fully understand the theory surrounding Hilbert’s fifth problem. Every so often, I encounter a basic fact in Lie theory which requires a slightly non-trivial “trick” to prove; I am recording two of them here, so that I can find these tricks again when I need to.
The first fact concerns the exponential map from a Lie algebra
of a Lie group
to that group. (For this discussion we will only consider finite-dimensional Lie groups and Lie algebras over the reals
.) A basic fact in the subject is that the exponential map is locally a homeomorphism: there is a neighbourhood of the origin in
that is mapped homeomorphically by the exponential map to a neighbourhood of the identity in
. This local homeomorphism property is the foundation of an important dictionary between Lie groups and Lie algebras.
It is natural to ask whether the exponential map is globally a homeomorphism, and not just locally: in particular, whether the exponential map remains both injective and surjective. For instance, this is the case for connected, simply connected, nilpotent Lie groups (as can be seen from the Baker-Campbell-Hausdorff formula.)
The circle group , which has
as its Lie algebra, already shows that global injectivity fails for any group that contains a circle subgroup, which is a huge class of examples (including, for instance, the positive dimensional compact Lie groups, or non-simply-connected Lie groups). Surjectivity also obviously fails for disconnected groups, since the Lie algebra is necessarily connected, and so the image under the exponential map must be connected also. However, even for connected Lie groups, surjectivity can fail. To see this, first observe that if the exponential map was surjective, then every group element
has a square root (i.e. an element
with
), since
has
as a square root for any
. However, there exist elements in connected Lie groups without square roots. A simple example is provided by the matrix
in the connected Lie group . This matrix has eigenvalues
,
. Thus, if
is a square root of
, we see (from the Jordan normal form) that it must have at least one eigenvalue in
, and at least one eigenvalue in
. On the other hand, as
has real coefficients, the complex eigenvalues must come in conjugate pairs
. Since
can only have at most
eigenvalues, we obtain a contradiction.
However, there is an important case where surjectivity is recovered:
Proposition 1 If
is a compact connected Lie group, then the exponential map is surjective.
Proof: The idea here is to relate the exponential map in Lie theory to the exponential map in Riemannian geometry. We first observe that every compact Lie group can be given the structure of a Riemannian manifold with a bi-invariant metric. This can be seen in one of two ways. Firstly, one can put an arbitrary positive definite inner product on
and average it against the adjoint action of
using Haar probability measure (which is available since
is compact); this gives an ad-invariant positive-definite inner product on
that one can then translate by either left or right translation to give a bi-invariant Riemannian structure on
. Alternatively, one can use the Peter-Weyl theorem to embed
in a unitary group
, at which point one can induce a bi-invariant metric on
from the one on the space
of
complex matrices.
As is connected and compact and thus complete, we can apply the Hopf-Rinow theorem and conclude that any two points are connected by at least one geodesic, so that the Riemannian exponential map from
to
formed by following geodesics from the origin is surjective. But one can check that the Lie exponential map and Riemannian exponential map agree; for instance, this can be seen by noting that the group structure naturally defines a connection on the tangent bundle which is both torsion-free and preserves the bi-invariant metric, and must therefore agree with the Levi-Civita metric. (Alternatively, one can embed into a unitary group
and observe that
is totally geodesic inside
, because the geodesics in
can be described explicitly in terms of one-parameter subgroups.) The claim follows.
Remark 1 While it is quite nice to see Riemannian geometry come in to prove this proposition, I am curious to know if there is any other proof of surjectivity for compact connected Lie groups that does not require explicit introduction of Riemannian geometry concepts.
The other basic fact I learned recently concerns the algebraic nature of Lie groups and Lie algebras. An important family of examples of Lie groups are the algebraic groups – algebraic varieties with a group law given by algebraic maps. Given that one can always automatically upgrade the smooth structure on a Lie group to analytic structure (by using the Baker-Campbell-Hausdorff formula), it is natural to ask whether one can upgrade the structure further to an algebraic structure. Unfortunately, this is not always the case. A prototypical example of this is given by the one-parameter subgroup
of . This is a Lie group for any exponent
, but if
is irrational, then the curve that
traces out is not an algebraic subset of
(as one can see by playing around with Puiseux series).
This is not a true counterexample to the claim that every Lie group can be given the structure of an algebraic group, because one can give a different algebraic structure than one inherited from the ambient group
. Indeed,
is clearly isomorphic to the additive group
, which is of course an algebraic group. However, a modification of the above construction works:
Proposition 2 There exists a Lie group
that cannot be given the structure of an algebraic group.
Proof: We use an example from the text of Tauvel and Yu (that I found via this MathOverflow posting). We consider the subgroup
of , with
an irrational number. This is a three-dimensional (metabelian) Lie group, whose Lie algebra
is spanned by the elements
with the Lie bracket given by
As such, we see that if we use the basis to identify
to
, then adjoint representation of
is the identity map.
If is an algebraic group, it is easy to see that the adjoint representation
is also algebraic, and so
is algebraic in
. Specialising to our specific example, in which adjoint representation is the identity, we conclude that if
has any algebraic structure, then it must also be an algebraic subgroup of
; but
projects to the group (1) which is not algebraic, a contradiction.
A slight modification of the same argument also shows that not every Lie algebra is algebraic, in the sense that it is isomorphic to a Lie algebra of an algebraic group. (However, there are important classes of Lie algebras that are automatically algebraic, such as nilpotent or semisimple Lie algebras.)

18 comments
Comments feed for this article
25 June, 2011 at 2:47 pm
RdN
As for surjectivity of exp, one thing you can probably do is first prove conjugacy of Cartans. Now it’s obvious that exp is surjective for a torus, and everything lives inside a torus.
25 June, 2011 at 3:03 pm
RdN
As for surjectivity of exp, one thing you can probably do is first prove conjugacy of Cartans. Now it’s obvious that exp is surjective for a torus, and everything lives inside a torus. (And here’s (http://math.berkeley.edu/~allenk/courses/spr02/261b/notes/symplectic3.pdf) a nice symplectic approach to conjugacy of Cartans.)
25 June, 2011 at 3:16 pm
Lior
More precisely, in a compact connected Lie group every element lies in a maximal torus (and these tori are all conjugate).
25 June, 2011 at 4:11 pm
Allen Knutson
Weird; I don’t see how to comment, only to reply.
The usual example of a non-algebraic group is the universal cover of SL_2(R). If it were algebraic, it would have a faithful finite-dimensional rep, which would descend to sl_2(R), complexify to sl_2(C), and extend to SL_2(C) (since that one is simply connected). But the map from the universal cover of SL_2(R) to SL_2(C) is not 1:1.
One nonalgebraic Lie algebra is the semidirect product of R acting on R^2 x R^2, rotating each factor but at incommensurable speeds. Then the adjoint orbits are irrational flows on tori, so not locally closed, which wouldn’t happen with an algebraic action.
[The comment reply box is at the very bottom of the page – T.]
26 June, 2011 at 9:41 am
Terence Tao
Thanks Allen! I have one stupid question; I thought it was only the affine algebraic groups that necessarily had finite-dimensional representations; does the above argument rule out the metaplectic group being an abstract algebraic group rather than an affine one?
27 April, 2018 at 10:32 am
Lior Silberman
Good question.
Every abstract algebraic group over a perfect field (such as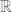 ) is an extension of an abelian variety by an affine (=linear) algebraic group (Theorem of Barsotti–Chevalley). On the other hand, metaplectic covers of groups such that
) is an extension of an abelian variety by an affine (=linear) algebraic group (Theorem of Barsotti–Chevalley). On the other hand, metaplectic covers of groups such that 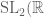 don’t surject on non-trivial compact Lie groups.
don’t surject on non-trivial compact Lie groups.
Now abelian varities are projective so their sets of real or complex points are compact. It follows that if a metaplectic group was the set of real points of an algebraic group it would be the set of real points of an affine algebraic group.
26 June, 2011 at 2:40 am
xavier
a little typo : you indicate pusieux instead of puiseux
[Corrected, thanks – T.]
26 June, 2011 at 6:03 am
Marius Buliga
It is interesting that:
A Connected Lie Group Equals the Square of the Exponential Image,
Michael Wüstner, Journal of Lie Theory. Volume 13 (2003) 307–309
Click to access wuestla2e.pdf
26 June, 2011 at 8:50 am
Allen Knutson
I should have mentioned: a nonalgebraic group that arises “in nature” is the metaplectic group. The Heisenberg group has an essentially unique irrep (via the Stone-von Neumann theorem) so the symplectic group, which acts on the Heisenberg, should act on that irrep too (by Schur’s lemma) — but only projectively (because of the possible scalar in Schur’s lemma). The group that actually acts is the metaplectic group, the double cover of symplectic. Since the representation is infinite-dimensional, it doesn’t force the metaplectic group to be algebraic.
27 June, 2011 at 12:24 am
elgeorges
A little typo: you write (in the sentence following its definition) that the matrix g is orthogonal, which it is not.
[Corrected, thanks – T.]
27 June, 2011 at 8:22 pm
Innerproduct
Another little typo in the fourth paragraph:
The circle group S^1, which has R as its Lie algebra…
[Corrected, thanks – T.]
29 June, 2011 at 7:09 am
mmailliw//william
As written for Example 2, I’m not sure the adjoint representation is the identity as you claim:
while Ad X indeed has the matrix representation of X, it looks like
Ad Y actually has the matrix representation of -Y (since [Y, X] = -Y and [Y, Y] =[Y, Z] = 0, the matrix representation for Ad Y should have a -1 where the matrix of Y has 1)
and similarly Ad Z has the matrix representation of -alpha Z.
That, though, would be fixed if we replaced Y with -Y and Z with -alpha Z in the original definitions, though: is this right?
[Corrected, thanks – T.]
17 August, 2011 at 7:04 pm
Notes on local groups « What’s new
[…] On the other hand, it is possible to eliminate the reliance on the Baker-Campbell-Hausdorff formula by using Frobenius’s theorem to construct the local Lie group instead; we omit the details. Remark 4 The above argument also reveals one advantage of local Lie groups over global ones; local Lie groups are locally linearisable (in the sense that they are isomorphic to a local subgroup of a linear group), whereas global Lie groups need not be globally linearisable, as discussed in this previous post. […]
27 August, 2011 at 11:35 am
254A, Notes 0 – Hilbert’s fifth problem and related topics « What’s new
[…] An important subclass of the closed linear groups are the linear algebraic groups, in which the group is also a real or complex algebraic variety (or at least an algebraically constructible set). All of the examples of closed linear groups given above are linear algebraic groups, although there exist closed linear groups that are not isomorphic to any algebraic group; see this post. […]
5 September, 2013 at 9:23 pm
Notes on simple groups of Lie type | What's new
[…] to each other also. On a compact Lie group, the exponential map is surjective (as discussed in this previous blog post); as every element in lies in a Cartan algebra, we obtain the useful fact that every element of […]
3 May, 2015 at 10:12 pm
The standard branch of the matrix logarithm | What's new
[…] for a more complete description of the image of the exponential map in classical groups, as well as this previous blog post for some more discussion of the surjectivity (or lack thereof) of the exponential map in Lie […]
8 May, 2015 at 9:18 am
254A, Notes 6: Large values of Dirichlet polynomials, zero density estimates, and primes in short intervals | What's new
[…] for a more complete description of the image of the exponential map in classical groups, as well as this previous blog post for some more discussion of the surjectivity (or lack thereof) of the exponential map in Lie […]
21 March, 2022 at 6:50 pm
Victor Wang Generals – scroo9ooge
[…] map (w.r.t. a bi-invariant metric) agrees with the Lie-theoretic exponential map, see e.g. https://terrytao.wordpress.com/2011/06/25/two-small-facts-about-lie-groups/ Other comments from S after the exam: – Conjugacy of maximal tori has to do with some […]