One of my favourite open problems in additive combinatorics is the polynomial Freiman-Ruzsa conjecture, which Ben Green guest blogged about here some time ago. It has many equivalent formulations (which is always a healthy sign when considering a conjecture), but here is one involving “approximate homomorphisms”:
Polynomial Freiman-Ruzsa conjecture. Let
be a function which is an approximate homomorphism in the sense that
for all
and some set
. Then there exists a genuine homomorphism
such that
takes at most
values.
Remark 1. The key point here is that the bound on the range of is at most polynomial in |S|. An exponential bound of
can be trivially established by splitting
into the subspace spanned by S (which has size at most
) and some complementary subspace, and then letting g be the projection of f to that complementary subspace.
Recently, Ben Green and I have shown that this conjecture is equivalent to a certain polynomially quantitative strengthening of the inverse conjecture for the Gowers norm ; I hope to talk about this in a future post. For this (somewhat technical) post, I want to comment on a possible further strengthening of this conjecture, namely
Strong Polynomial Freiman-Ruzsa conjecture. Let
be a function which is an approximate homomorphism in the sense that
for all
and some set
. Then there exists a genuine homomorphism
such that
takes values in the sumset
for some fixed
.
This conjecture is known to be true for certain types of set S (e.g. for Hamming balls, this is a result of Farah). Unfortunately, it is false in general; the purpose of this post is to describe one counterexample (related to the failure of the inverse conjecture for the Gowers norm for for classical polynomials; in particular, the arguments here have several features in common with those in the papers of Lovett-Meshulam-Samorodnitsky and Green-Tao). [A somewhat different counterexample also appears in the paper of Farah.] The verification of the counterexample is surprisingly involved, ultimately relying on the multidimensional Szemerédi theorem of Furstenberg and Katznelson.
(The results here are derived from forthcoming joint work with Ben Green.)
— Description of counterexample —
We let n be a large number, and replace by the
-dimensional vector space V of quadratic forms
(with a basis given by the monomials
with
). We let
be defined by the formula
.
A brief computation shows that for any , the quadratic form
is of rank at most three, by which we mean that it is a function of at most three linear forms. More specifically, we have
(1)
where
Thus, if we let S be the space of quadratic forms of rank at most 3, the hypotheses of the polynomial Freiman-Ruzsa conjecture hold.
— Verification of counterexample —
To establish the counterexample, we assume for contradiction that there exists a linear function such that
has bounded rank for all h, and deduce a contradiction (for n sufficiently large).
By hypothesis, we have linear forms for all
and some
and coefficients
for all
such that
and in particular (by (1) and linearity of g)
. (2)
The key point is that the linear forms are usually “independent” of the linear forms
. The key lemma in this regard is
Lemma 1. If h, k are selected uniformly and independently at random, then with probability 1-o(1),
is not a linear combination of the
. Similarly for
.
Proof. By cyclically permuting h,k,h+k it suffices to show this for . Since there are at most O(1) possible linear combinations amongst the
, it suffices to show that for any given assignments
of linear forms, that the probability of the event
(3)
is o(1). Suppose for contradiction that the event (3) holds for a set E of pairs (h,k) in of positive density. Applying the Furstenberg-Katznelson multidimensional Szemerédi theorem) we can find (for n large enough) a square
in E with r non-zero. Applying (3) for all four pairs and summing, we obtain
(recall we are in characteristic 2). But the left-hand side is equal to the linear form , which is non-zero, a contradiction.
Now we can obtain the desired contradiction. For a generic choice of h,k, we now know that none of the are linear combinations of the
. Thus, on a given level set of the
(which form a subspace of
), the linear functions
are non-constant, and so the range of the triplet
must be an affine subspace of
which is not contained in any plane in
that is parallel to the two of the coordinate axes (i.e. of the form
,
, or
. This forces the subspace to be parallel to (1,1,1). But this implies that
is non-constant on this space, contradicting (2).
Remark 2. The function f appearing in the above example is closely related to the symmetric polynomial
.
Indeed, one can show that the derivative of
is equal to
, plus some additional terms which involve only a finite number of linear forms, and the quadratic polynomial
. If it was the case that
could be approximated by a linear map
modulo low rank errors, then it one could use this to eventually show that
correlated with a cubic polynomial; but it is known (from the papers of Lovett-Meshulam-Samorodnitsky and Green-Tao) that this is not the case. Thus there is an alternate way to verify that the above example is indeed a counterexample to the strong polynomial Freiman-Ruzsa conjecture.

7 comments
Comments feed for this article
11 November, 2008 at 6:56 pm
bengreen
Terry,
I know that your blog has a wide readership and so it would be irresponsible of me to endorse gambling in any way. However I should perhaps mention the informal bet I had with Jean Bourgain, whereby he wins 100 dollars from me if a counterexample to PFR is found and I win the same if a proof of the conjecture is found within 5 years.
This counterexample to the `strong’ form of the conjecture (which I knew about before making the bet….) does suggest that a proof of the statement might have to be a little weird.
I’d like to take this rare opportunity to use the word `cohomology’ on your website (or indeed at all). Emmanuel Breuillard pointed out to me that there is this thing called bounded cohomology, which roughly speaking measures the obstruction to maps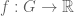 with
with  being a bounded distance from genuine homomorphisms. Apparently quite a lot of the theory is developed in a paper of Gromov which I have yet to obtain. See also an article by Kotschick in Notices of the AMS, vol 51. no .2 called “What is a quasimorphism”?
being a bounded distance from genuine homomorphisms. Apparently quite a lot of the theory is developed in a paper of Gromov which I have yet to obtain. See also an article by Kotschick in Notices of the AMS, vol 51. no .2 called “What is a quasimorphism”?
Perhaps `Ruzsa cohomology’ can resolve these issues but suddenly 5 years looks like a very short period of time :-)
Ben
9 March, 2009 at 5:04 pm
Harald
Hi –
I think there are a couple of mistakes. The definitions of a_{h,k}, b_{h,k} and c_{h,k} after equation (1) can’t be right. What are the right polynomials? In the section right thereafter, all occurences of L_{h,d}, L_{k,d}, L_{h+k,d} should be
L_{h,j},L_{k,j}, L_{h+k,j} instead.
9 March, 2009 at 5:25 pm
Terence Tao
Thanks for the correction! The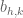 was missing a
was missing a 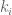 in their definition; I’ve fixed it now.
in their definition; I’ve fixed it now.
9 March, 2009 at 11:25 pm
Harald
Also – what does “any coordinate plane” mean? Does that mean the xy, yz, xz planes? If so, how does the fact that the range of (a_{h,k},b_{h,k},c_{h,k}) is not contained in one of those imply that it is at least two-dimensional?
Harald
10 March, 2009 at 7:43 am
Terence Tao
Dear Harald,
By coordinate plane I meant the planes in in which x, y, or z is held constant. The only one-dimensional spaces which are not in coordinate planes are those lines in the direction (1,1,1), but ab+bc+ca is not constant on those lines. I’ll reword the argument there to make it a bit clearer.
in which x, y, or z is held constant. The only one-dimensional spaces which are not in coordinate planes are those lines in the direction (1,1,1), but ab+bc+ca is not constant on those lines. I’ll reword the argument there to make it a bit clearer.
20 June, 2009 at 9:55 am
An equivalence between inverse sumset theorems and inverse conjectures for the U^3 norm « What’s new
[…] Math. Proc. Camb. Phil. Soc.. The main result of this short paper (which was briefly announced in this earlier post) is a connection between two types of inverse theorems in additive combinatorics, namely the […]
19 March, 2014 at 5:30 pm
Metric entropy analogues of sum set theory | What's new
[…] due to the failure of a certain strong version of Freiman’s theorem, as discussed in this previous post); nevertheless, the proofs of the discrete arguments are elementary enough that they can be […]