Now that the project to upgrade my old multiple choice applet to a more modern and collaborative format is underway (see this server-side demo and this javascript/wiki demo, as well as the discussion here), I thought it would be a good time to collect my own personal opinions and thoughts regarding how multiple choice quizzes are currently used in teaching mathematics, and on the potential ways they could be used in the future. The short version of my opinions is that multiple choice quizzes have significant limitations when used in the traditional classroom setting, but have a lot of interesting and underexplored potential when used as a self-assessment tool.
— Multiple choice quizzes in the classroom —
In principle, it would seem that the unambiguous and precise nature of mathematical statements would lend itself well to the multiple choice format; in contrast to some other disciplines of knowledge, many questions in mathematics do have a single and objective correct answer, with all other answers being agreed upon as being incorrect. With a multiple choice quiz, a student can be tested on such questions in an objective manner; indeed, the grading for such quizzes can even be automated to be done by a computer or scanning machine. As long as the question was phrased unambiguously (and that the solution key is correct), the grading of such quizzes is less subject to dispute than other means of examination. As a final positive, the multiple choice format is extremely familiar to virtually all college students (who have probably had to have taken standardised multiple choice tests as part of the university admission process) and so the rules of the quiz require very little explanation.
On the other hand, the multiple choice format, as it is currently used in maths exams, has a number of serious weaknesses which, in my opinion, render it inferior to other examination options for most upper-division maths courses, although there are ways to remove the most glaring defects of the format. Perhaps the most obvious problem is the zero-tolerance approach to mistakes, which can distort the relationship between aptitude and credit: a student who had the right approach to a question, but made a single sign error or misunderstood the question slightly, could lose all points for a question, whereas a student who had no clue whatsoever what to do, and is simply guessing randomly, could manage to earn credit for a multiple choice question by pure luck, which is much harder to achieve in other examination formats. (Admittedly, one can mitigate this problem by keeping the questions simple and unambiguous, and ensuring that the incorrect answers obtainable from sign errors and the like are not given as one of the alternatives.) Another issue is that multiple choice quizzes are more susceptible to certain types of cheating and corruption than other examination formats, since the answer key is easy to copy and use, even by students who do not actually understand the material. (This particular problem can be guarded against to some extent by shuffling the questions separately for each student, though this of course makes it more difficult to grade the quiz, or to provide a solution key afterwards.) A third problem is that if the student arrives at an answer that is not among the options listed, this often encourages a rather tortured and not particularly logical fudging of the computation in order to arrive at one of the listed answers, which is not a good habit to instill in a mathematician.
A more insidious problem, however, is that these quizzes give a misleading impression of what mathematical problem solving is, and how one should go about it. In actual mathematical research, problems do not usually come with a list of five alternatives, one of which is correct; often, figuring out what the potential, plausible, or likely answers could be, or even what type of answers one should expect or whether one should ask the question at all, is as important as actually identifying the correct answer. Multiple choice quizzes also tend to reward quick-and-dirty or sloppy approaches to problem solving, as opposed to careful, deliberate, and nuanced approaches; in particular, such quizzes tend to encourage the mindless application of formal rules in order to arrive at an answer, without devoting much thought as to whether these rules are actually applicable for the problem at hand. (Indeed, overthinking a multiple quiz problem, searching for some subtle trick, degeneracy, or exception in the wording of the problem, or trying to play some sort of “metagame” in which one is trying to divine the intent of the examiner [see this scene from “The Princess Bride” for an extreme example of this], can mean that the brighter students who actually understand the material can end up doing worse on the quiz than those who are simply applying the rules they are taught without that understanding. Conversely, an overly tricky quiz problem that is designed to trap those who carelessly apply a standard rule without checking to see that it applies will usually be (quite rightly) perceived as being rather unfair on the student.) While some drill of basic formal rules (e.g. the laws and algorithms of calculus) is certainly necessary, especially at the high-school and lower-division undergraduate levels of mathematics, by the time one transitions to upper-division mathematics, one needs to start understanding the underlying theory and justification behind such rules, as part of developing a more conceptual grounding in the subject. (Also, when one gets to more advanced topics, there tend to be so many exceptions and weaknesses to any given rule that it becomes quite dangerous to apply such rules mindlessly. For instance, computing an integral by unilaterally shifting contours is quite likely to give an incorrect answer if one does not have a good sense of which contour integrals will safely go to zero in some limit, and which ones do not. It is self-defeating to look for some easily memorised rule that will say which integrals are safe and which ones are not, as there are so many different variations, especially in real-world applications; the only reliable way to proceed is to actually understand the business of estimating integrals and computing limits.)
But perhaps most of all, multiple choice questions promote the idea that the answer to a mathematical question is more important than the process used to arrive at that answer (and the insights acquired during that process, and the art of communicating that process effectively to others). In truth, the process is far more important than the answer, particularly if the answer is to an artificial question, such as one designed specifically for examination purposes. Knowing the thought processes that were used by a student to arrive at an answer – even an incorrect one – would give me a detailed picture of how well equipped the student would be to handle similar (or more complicated) questions in the future, whereas the mere knowledge that the student selected one correct answer out of five alternatives gives me much less information in this regard. This also allows for much more valuable feedback in the grading process than simply reporting whether a given question was answered correctly or incorrectly, by identifying specific strengths and weaknesses in a student’s reasoning.
— Multiple choice quizzes as self-examination —
I have discussed my reservations about the use of multiple choice quizzes in classroom examinations, particularly in upper-division mathematics courses. On the other hand, I do feel that such quizzes can play a very useful supporting role in self-examination for such courses, particularly with regards to foundational material (e.g. definitions or basic rules of calculation). I will illustrate this with a hypothetical course in high school algebra, though the point is certainly applicable to more advanced mathematical courses.
Suppose this algebra course is intended to teach students how to solve various algebraic equations. There are of course several standard pitfalls that the student encounters when actually trying to solve such equations; a common one is starting with an equation such as and concluding incorrectly that
, when instead the best one can say is that
or
. Now, one can caution against this error in classes, and the student may even write down this warning when taking notes, but it still happens all too frequently that this error is committed while solving a more complicated algebra problem in an examination (or worse, in a real life application of one’s high school algebra). At that point, the student may well realise the cause of the error – but this feedback may come days or weeks after first learning the material; without reinforcement, the same error may then recur later in the course, or in subsequent courses. Repeated exposure to algebra will eventually eliminate the error, but it can be an inefficient process.
This is where a self-administered multiple choice quiz (in particular, an online quiz) can help, with questions such as
Question 1. If x and y are real numbers such that
, then the best we can say about x is that
.
.
.
or
.
or
.
mixed together with variants such as
Question 2. Let x and y be real numbers. Which of the following statements is not sufficient to imply that
?
.
.
- x is either equal to
or
.
.
.
and
Question 3. If x and y are real numbers such that
, then the best one can say about x is that
.
.
or
.
.
or
.
Such questions can address quite directly (and with immediate feedback) whether one has any misunderstanding on this specific point, without needing the live intervention of a lecturer or teaching assistant. (Ideally, an automated quiz should not only respond immediately as to whether the selected answer was true or false, but also to explain what the error was in the latter case.)
Note some differences between these sorts of multiple choice questions and the ones that appear in a classroom examination. In an exam setting, one usually wants to have more complex questions that test several aspects of the material at once (e.g. factorisation, gathering terms, substitution, etc.) rather than focusing narrowly and simply on a single aspect. (In particular, a student who actually knows the material should be able to answer each question here readily, without the need for significant computation.) Also, while classroom quizzes take pains to make the correct answer quite distinct from the incorrect alternatives (to separate those who basically understand the material from those who are truly lost), it is more effective for self-examinations to have only quite subtle differences between the correct answer and the other answers, in order to encourage the student to think carefully and to address any misconceptions head-on; these kinds of “trick questions” would be rather unfair in the stressful environment of an assessed classroom exam, but can be safely administered in a self-examination.
Multiple choice questions seem most effective here for reinforcing the precise definition of a key concept (was it “For every there exists a
“, or “for every
there exists an
?”), the precise formulation of some rule (is the derivative of
equal to
, or
, or
, etc.?), or the direct testing of a specific and commonly made error (if
, does this imply that
, or
? See also this list of common errors in college maths). But with a bit of imagination, one could come up with some useful multiple choice questions for self-examination for other purposes, even for rather advanced maths topics. For instance, consider the following question to test one’s grasp of the properties of the Fourier transform:
Question 4. Let
be a function. Among all the hypotheses listed below, which one is the weakest that still implies that the Fourier transform
exists and is continuous?
- f is smooth and rapidly decreasing.
- f is absolutely integrable.
- f is square-integrable.
- f is continuous.
- f is continuous and compactly supported.
- f is a tempered distribution.
The type of knowledge in Fourier analysis that this question is probing seems difficult to examine by other types of questioning (other than an oral examination).
Another interesting possibility is to use multiple choice quizzes to explore specific mathematical problem solving tactics, which is an issue which is only indirectly addressed by most examination methods. For instance, in a single-variable calculus course, one could focus on integration tactics, using questions such as these:
Question 5. Which of the following techniques would you feel to be a good first step towards finding an antiderivative
of the function
?
- Integration by parts, differentiating
and integrating
.
- Integration by parts, differentiating
and integrating
.
- Substitution, setting
.
- Substitution, setting
.
- Substitution, setting
.
- Trial differentiation, using functions such as
.
- Sketching a graph of
.
- Taylor series expansion of
.
- Start up Maple, Mathematica, or SAGE. :-)
Note that this question is of a more subjective nature than the preceding questions, with different answers having different strengths and weaknesses; there is no single “correct” or even “best” answer here. As such, this would be a terrible question to place in an assessed exam, but I think it would be a good thought-provoking question to give in a self-administered quiz. (This would be one example of a question where the process of arriving at one’s chosen answer is definitely more valuable than the answer itself. Also, having a place to discuss the various answers to a question such as this – as would be the case, for instance, if the question was hosted on a wiki – would also add an extra dimension to this exercise.) Note the difference between the above question and the more traditional “Compute the antiderivative of .”; the emphasis is now on tactics rather than computation.
In summary, I believe that there are a number of interesting ways – many of which appear to be underexplored at present – in which some well-designed and self-administered online multiple choice questions can efficiently assess one’s strengths and weaknesses in a given mathematical subject. Of course, having one-on-one interaction with a lecturer or teaching assistant would be a greatly preferable way to achieve this sort of instant feedback, but this is impractical for larger classes. It is also true that a certain level of maturity and discipline is needed on the student’s part in order to actually benefit from these sort of self-assessments, especially since they are not directly contributing to the student’s grade in the class, but my philosophy here is to give the students the benefit of the doubt in this regard; I feel that being able to explore beyond the bare minimum of what is needed to obtain a passing grade is part of what an upper-division course should be about.

48 comments
Comments feed for this article
14 December, 2008 at 12:46 am
David
As a European currently applying for graduate school in the US I was surprised to find out I needed to take multiple choice tests like the GRE subject math exam at this stage in my education. Do you think the benefit of having a standardised test to asses all candidates, which is also easy to administer, outweighs the various drawbacks mentioned in your post?
14 December, 2008 at 2:36 am
Harald Hanche-Olsen
I suppose algebra lends itself more easily to this sort of feedback more readily than other areas of mathematics, blurring the line between quizzes and tutorial software. For what seems to be a good example of the latter, check out Theory Y Algebra.
14 December, 2008 at 3:46 am
Dan
You sound like you should be using Moodle, which was started by a fellow Australian. It seems pretty easy to have multiple choice quizzes that the students use for self-assessment. Your ideas above seem to mesh with their ideas of “social constructivism”.
I have used Moodle for a graduate class and found it pretty easy and flexible. I recommend giving it a try.
Also, I’m glad to see Sage mentioned alongside Maple and Mathematica…
14 December, 2008 at 6:29 am
anonymous
Why should multiple choice tests be used in mathematics courses?
a.) According to the “Does one have to be a genius” section of this blog, luck
is one of the essential ingredients in doing mathematics.
b.) It would allow the University of South Queensland to replace all its remaining
faculty with automatons.
c.) According to the axiom of choice, the test can be completed independent of its
cardinality.
d.) All of the above.
e.) None of the above
14 December, 2008 at 8:45 am
Larry Sheldon
An Off-the-topic question: When did (or where did) the practice of using the plural of “math” (as in “…as it is currently used in maths exams…” above) begin?
I don’t remember hearing it before a year or two ago. (I should say that we have documented evidence of my failure to pay attention in Mathematics classes, although I personally think the problem had more to do with a failure to do the homework).
5 May, 2014 at 2:02 am
AngeloPardi
Maths : British
Math : American
Interestingly, French people use the plural “les mathématiques”, shortened as “maths”
1 February, 2017 at 2:38 pm
Romain Viguier
It is because before, music was part of the mathematics so we used the plural.
14 December, 2008 at 9:04 am
Mark Meckes
I think there’s a hat missing is Question 4. [Corrected – T.]
As a silly aside, I’d point out that there are some real math problems that have a multiple choice form. For example, say I need to know the dimension of some subspace of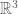 .
.
14 December, 2008 at 9:04 am
Beetle B.
An Off-the-topic question: When did (or where did) the practice of using the plural of “math” (as in “…as it is currently used in maths exams…” above) begin?
In British English (and I can only assume, Australian English), they say “maths” and not “math”. It’s not a plural of the other.
14 December, 2008 at 3:46 pm
Robert
A lot of the usefulness of multiple choice tests I think depends on the care that is taken picking the “incorrect” answers. If you guess which mistakes would likely be made you could have appropriate answers. If the wrong answers are just random answers there is no need for those since nobody will come up with those in a true calculation only by guessing an answer if he/she has no clue at all.
In addition there are the types of meta-thoughts the student could have: For example in maths olympiads you could ofthen get an idea how to approach the question by using the fact that this was an olympiad question, i.e. it had to have a unique answer and usually there is a cute way of finding it. This often ruled out many dull things one would have tried otherwise.
Also, often the possible answers give something away: In question 1, anybody who actually reads all the possible answers and has only heard the waring one will remember that -sqrt(y) has to be considered as well once he sees this is a possible answer. If there were a problem where at some point x^2=y had to be solved for x and the possible answers would not suggest that one has to take care of the sign many more people would forget about -sqrt I would believe.
Similarly, question 2 is a no brainer since obviously only one answer can be correct and that one is obvious. One does not have to think about signs of squar roots to find x=y^2 as wrong. It would be better if it were not known in advance that only one answer is correct and some answers need several answers to be ticked.
But even when “proper” questions are asked (instead of multiple choice) I still believe oral exams are much superior to written ones: In my experience the grades in written exams cluster much more in the middle since there will always be “questions for everybody”. Some of the questions will be very easy and thus not eb discriminating between candidates. And even very good students will have a hard time getting exactly everything right and not doing some stupid mistake somewhere in the middle.
On the other hand I believe in the ideal oral exam the student can answer exactly have the questions right. But it is of course the questions that adopt to the student. By doing this the examinors can precisely map out the boundary of the student”s knowlede without wasting too much time by asking very good students trivial questions or poor students too hard ones.
Unfortunately, the work to have oral exams scales very badly for large number of students.
14 December, 2008 at 4:27 pm
heatkernel
Somewhat off-topic, but I think sufficiently related to the topic of this post to warrant asking this here: has anyone come across any good advice about how to structure and grade exams in proofs-based courses? I taught for the first time, an advanced undergraduate class (point-set topology) this semester. Since for many of the students, it was their principle introduction to proofs-writing and proof-centered mathematics, I made all the exams primarily consist of statements for them to prove. In order to bring about some consistency in the grading, I tried to come up with “grading schemes” awarding different point values to different parts or steps of the proofs. The problem is that, even though all the questions were very similar if not identical to exercises in the homework or the book’s theorems, on every question a most of the students (with the exception of the same small set of harder working or better prepared students) flailed around all over the place and submitted a combination of true, false, and nonsensical statements that didn’t exactly add up to a proof, but demonstrated usually at least some knowledge of the subject. Although obviously, it is still necessary to assign some partial credit in such situations, it can be very difficult and time consuming to do so in a consistent and fair manner. I just wondered if anyone had come across anything helpful on the web or in the literature by anyone who has put some thought into the question of how to structure and grade proofs-based exams and has come up with some helpful suggestions.
14 December, 2008 at 4:48 pm
jelations
I’m not taking math, but I did notice this part —
“(Ideally, an automated quiz should not only respond immediately as to whether the selected answer was true or false, but also to explain what the error was in the latter case.)”
We don’t have this immediately since some of our MCQ online quizzes are graded, but shortly thereafter we sometimes get to see where we went wrong; and I must say that the times when they actually explain it = times when I’m most grateful! :D
14 December, 2008 at 11:39 pm
grant czerepak
Really what you are making a good attempt to explain is this:
Multiple choice questions are convergent and rarely experienced in real life, while problem solving is often divergent where there may be multiple paths to the single answer.
My most vivid memory is solving all the statistical questions in a chemistry exam using calculus only to be asked by the professor afterward how I came to arrive at non-statistical solutions. Wondering what kinds of idiots I was being taught by led me to change majors.
14 December, 2008 at 11:59 pm
carissa
I too find multiple choice in mathematics to be tricky, they are terribly misleading, and I especially relate to it when you say talk about the student who had the right approach but simply made a small mistake somewhere in the middle, something I’ve done too many times, but have been saved the deduction point because my teacher saw my calculations and was kind enough to give me points for it.
15 December, 2008 at 1:37 am
dodingdaga
I find the multiple choice exams in mathematics extremely difficult since it gives all the credit to the final answer and not to the solution which is very important.
One student can get the correct answer by guessing without even looking at the question and a student who studied hard for the exam who had a solution amounting to short bond paper but failed to correctly answer the question since he had the wrong sign for the final answer.
15 December, 2008 at 4:05 am
Anonymous
My first comment is that I think that a very carefully designed multiple-choice test can test almost anything you want to test, with different partial credit for different wrong answers if you like.
My second comment is that there are even better ways to design a test to make it easy to grade, by careful choice of questions and the size of the space where the student must put the answer.
15 December, 2008 at 10:38 am
Anonymous
Here’s a standard SAT multiple choice question:
What’s next in the sequence:
1, 2, 4, 9, 25, 36 (*)
Typically they are going for the fact that these are all squares and the next number is 49. However this has always struck me as a poorly thought through question (despite the fact that variations of it are frequently recurring). f(x)=x^2 is an arbitrary polynomial, and each of the other answers will corespond to evaluation of some polynomial at consecutive integers.
The first thing that jumps out at me when i see sequence (*) is that they are all squares, but then again I spend a fair amount of time thinking about number theory. Who am I (or rather the guys at the college board) to say that this is the best answer? Is this really what college admissions should be based on?
15 December, 2008 at 1:47 pm
Harald Hanche-Olsen
Um, 2 is a square? Interestingly, even the on-line encyclopedia of integer sequences drew a blank on that one. (I am sure you didn’t mean to include 2 in the sequence, and most readers of this blog will catch it, but others might be puzzled, so I figured I might point out the mistake.)
15 December, 2008 at 2:28 pm
Michael Lugo
Robert,
I have recently been doing some private tutoring for some students taking a calculus class. The old final exams have been made available to the students, and these are all multiple-choice, so I’ve been spending a fair bit of time with them working through questions from the old exams. It is interesting to me to see how many of the multiple choice questions just have essentially random numbers as the distractors. I suspect that the writers of the tests in question would have preferred to write an exam that was not multiple-choice, but chose the multiple-choice format solely for ease of grading.
As for oral exams, the math PhD program here at UPenn (like at many other schools) has an oral qualifying exam, usually taken sometime during the second year. A lot of my friends are preparing for these exams right now. I’ve told them that they will feel stressed during the oral exam unless they are extraordinarily well prepared, because the examiners generally can quickly figure out the limits of what the examinee knows. So the majority of the time during the oral exam is spent flailing about, even for people who know what they’re doing.
Oral exams scale poorly, as you point out. One problem which is related to the scaling is that the real strength of the oral exam is that you can ask different questions to different students, depending on their level of knowledge. But if you do this, then can you really say that student A did better than student B? Student A may have answered less questions correctly than student B, but they were harder questions. This seems like it would be an issue in using such exams in a course. And even if the instructor feels that they can confidently rank students, I’m not sure the students would share that feeling. This isn’t a problem for higher-level exams like the PhD qualifying exams, from what I’ve seen. The purpose of the qualifying exam is to certify that the student is ready to begin research, and so each student is tested on a syllabus which is created by the student and their exam committee (three professors). By the time we get to taking orals our various programs have diverged, so very few pairs of students have identical syllabi. Furthermore, there are only three possible grades (pass, marginal pass, and fail) so the issues of measurement that would come up in grading for a course aren’t a problem here.
15 December, 2008 at 2:29 pm
Michael Lugo
Anonymous (10:38 am):
assuming you meant the sequence 1, 4, 9, 16, 25, 36, you could argue that the best description of the sequence is f(x) = x^2, and so the best “next term” is 49, essentially because the description f(x) = x^2 is very short, or alternatively because a program to generate that sequence is very short. This is basically the idea of Kolmogorov complexity. And I think there may be a place for questions such as this in admissions testing. I admit that these sequence completion questions can be a bit subjective, but the ones that make their way onto tests never seem to be. Besides, ambiguity is a part of life.
15 December, 2008 at 3:10 pm
notedscholar
I think that if multiple choice tests were completely eliminated from mathematics, we might see good results. We’d see less people succeeding, but the people who did succeed would be the cream of the crops.
On the other hand, in order to be truly egalitarian (which is the goal eventually!) perhaps we should allow multiple choice.
NS
http://sciencedefeated.wordpress.com
15 December, 2008 at 6:11 pm
Jonathan Vos Post
I may have something serious to say later, as a former Adjunct Professor of Mathematics who specialized in teaching students who’d flunked remedial algebra once, twice, even thrice.
But, for now, in answer to anonymous’s pseudo-SAT problem, I’d skip the 49 and go ahead with 121. Because of the integer sequence by Klaus Brockhaus:
Records in A111390
1, 2, 4, 9, 25, 49, 121, 625, 841, 961, 1369, 1681, 1849, 2209, 2401, 4096, 59049, 531441, 9765625, 244140625, 282475249, 282811489, 283484569, 283518244, 283619281, 283787716, 283821409, 284023609, 284091025, 284192164, 284225881
Of course, that presumes that one likes
A111390 a(1)=1. a(n) = smallest positive integer not occurring earlier in the sequence such that |d(a(n))-d(a(n-1))| = 1, where d(n) is the number of positive divisors of n.
The point is well taken, though, that the more Math one knows, the more that the “wrong” answers can be justified.
I’d add that the key to effective education, including in Math, and including self-education, is to maintain a proper balance oif:
(a) instruction;
(b) management;
(c) assessment.
15 December, 2008 at 6:42 pm
erik davis
The professor for my introductory topology course (basics of general topology with a bit of fundamental group and covering spaces) took a hybrid approach to exams. 80% of the exam grade was from 3-4 typical proof-oriented problems, and then there were 20 true/false questions accounting for the remaining 20% of the grade. The problems were usually straightforward — the majority would be things that had been explicitly covered in class, or else things that should be blatantly obvious to a student by that point. There would always be a few of them that were more substantial, in fact I would usually do a rough outline of a proof on scratch paper just to make sure I was not botching anything.
The purpose of these problems was, I think, to add some breadth since due to time constraints we couldn’t really write up a whole lot — the tests lasted only 50 minutes. I enjoyed them and appreciated the fact that they rewarded being able to think quickly when necessary. The obvious downside is that students can just guess on the problems, but the fact that they were only 20% of the grade reduced the effectiveness of this strategy — if you didn’t know your stuff, you could still fail pretty hard.
15 December, 2008 at 6:43 pm
matt
On the other hand, the problem with written tests is that the professor often wants to see you do the answer in a certain way. I slept through most of my differential geometry class as an undergrad, and was kind of stuck on the test since I hadn’t really learned much (or anything). By using (ugly, explicit, brute force) coordinate approaches, I was able to solve all or almost all of the questions, but got basically a zero because I didn’t solve any of them in the (more advanced) ways that had been taught. Had to go talk to the guy in person to explain to him that my final answer was correct in almost every case. Multiple choice would have been nicer.
15 December, 2008 at 6:45 pm
matt
Just to follow up that last one: if the prof wants to see the use of certain techniques, the problems should be set correctly. I took Serge Lang’s course in complex analysis, and he was upset that a lot of the class didn’t use contour integration to work out complex integrals on the first test (probably even threw some chalk), but then he realized that he should have just set more difficult integrals that would require contours.
15 December, 2008 at 8:48 pm
multiple choice tests are: (a) totally useless, (b) ideal for all classrooms, (c) useful in some situations, or (d) all of the above « orgtheory.net
[…] a comment » The answer is (c), if you read Tereance Tao’s post. He makes the case that there’s a good place for multiple choice questions in learning, just […]
16 December, 2008 at 9:42 pm
Jonathan Vos Post
Erik Davis makes an important point: “I enjoyed them [tests with time constraints] and appreciated the fact that they rewarded being able to think quickly when necessary.”
I challenge my disadvantaged high school Science students, and before them my university and high school Math students, by giving them both short quizzes (5-10 questions) which they can master, and longer (also tricky) multiple choice tests with 20-30 questions that almost none of them can complete in time. The latter are to force them to develop better strategic test-taking skills, such as triage.
First skim each question on the entire test, and put a pencil check mark next to the ones that look easy. Do all the easy ones first. If you run out of time later, at least you have done the ones that looked easy to you, so if your easiness-estimator is good, you have an expectation of many answers correct. Then skim the remaining questions and tick the ones that look hard. Ignore them for now, and do the remaining intermediate-hard questions. Don’t mess with the hard questions unless you finish all the easy and intermediate questions before the deadline.
Also: eliminate the obviously silly answers and, if you narrow things down to two possibilities, guess. Also: look for questions which give you information to answer other questions.
College student have practiced many of these strategies. Students in good high schools may have, also. Students in bad high school usually have done none of the above.
They complain that my tests aren’t fair. I tell them that life isn’t fair; get used to it. They complain that my tests are too hard. I tell them that life is hard; get even.
I still haven’t discussed multiple choice exams as such, but this gives some points not just about “think[ing] quickly when necessary” but about resource management, including time and computational capability as resources.
This now connects with the thread about how to write papers, and the resource management issues of co-authorship and making progress in a portfolio of solo papers across a spectrum of difficulty.
One purpose of assessment is connected with one purpose of instruction: I (as a teacher) am not telling you WHAT to think, I’m showing you HOW to think.
22 December, 2008 at 11:07 am
Soddisfazione « In teoria
[…] scoprire che Terry Tao la pensa (sostanzialmente) come me: vedere il suo pensiero in materia in questo […]
5 January, 2009 at 3:53 am
Prasad yadav
please i want to take a test now
2 February, 2009 at 9:05 am
AISHA
YA IT IS GOOD. I AM READY FOR TEST…………………………
24 February, 2009 at 11:38 am
TAYEM
I LOVE SUCH EFFORTS TO ENABLE STUDENTS TO STUDY EASILLY ONLINE.PLEASE I’LL LOVE TO GET SOME EXERCISES FROM HERE.
3 April, 2009 at 4:39 am
salman abbas
I want to take exam as soon as possible
12 June, 2009 at 10:13 pm
Anonymous
Do you think you could turn off the annoying “snap shots” on this blog? I finally found instructions on how to do it:
http://www.blork.org/blorkblog/2008/03/31/how-to-disable-snap-shots-on-blogs/
[Snap shots has been disabled for about a month or so here. If others are still finding it activated, please notify me. -T.]
29 June, 2009 at 7:42 am
Gérard P. Michon
Not all multiple-choice questions are bad. However, students who have been routinely rewarded for speed with little or no “penalty for guessing” often miss the point of well-designed questions, like this superbly crafted example (not mine ;-) where actual thinking IS required and rewarded:
The source of every sound is something that is
A) undergoing simple harmonic motion.
B) accelerating.
C) a net emitter of energy.
D) moving.
E) vibrating.
http://answers.yahoo.com/question/index?qid=20080809103803AApEWeK
Apparently, fewer than 20% of “guessers” pick the ONLY correct choice (C) because most or all wrong answers may look better, or more “plausible” at first.
Questions of that quality being so rare, it’s still safe to say that multiple-choice exams are a disgrace (except, possibly, in quick self-evaluations).
Also, let’s not forget that exams graded by a teacher are a rare opportunity for students to assert themselves in a creative sense. That opportunity is denied to them if they are only asked to check boxes…
The Big Picture: Education consists in passing civilization and knowledge from one generation to the next. Ultimately, some students ought to be able to write better questions than their elders, or else the whole exercise is pointless and/or doomed… Checking boxes in front of existing questions does not help at all in that process.
4 September, 2010 at 3:29 pm
Manoj Srinivasan
Gerard:
Your “source-of-sound” question, and especially what you call the correct answer, sounds a bit fishy to me.
You say every source of sound is a net emitter of sound.
Take some big machine (like a computer, say), that eats a LOT of energy (that is, work is performed on it), and produces a TINY little bit of sound. Such a machine would be emitting sound, but will be a net absorber of energy. So not all sound emitters are ‘net’ emitters of energy.
In fact, THE quintessential emitter of sound — a speaker — typically has about 1% efficiency. That is, 99% of electrical power input gets converted to heat. Now if you carefully heat-insulate the speaker, the speaker would be a very good net absorber of energy.
Anyway, I think one should carefully define what “a source of sound” means, before asking/answering this question.
21 October, 2013 at 3:54 pm
Anonymous
Well, then the speaker will stop working from overheating…
18 August, 2011 at 3:27 am
vishnu kumar
i wants to more examples
7 December, 2011 at 12:38 am
PETER MWALIMU MWENDWA
Rarely will you find life challenges well packaged into two, three or five sets of choices from which to pick one’s option. In the same vein, if mathematics is to be effectively used to enable persons to make useful decisions in life, then assessment should not be a package of choices for every problem posed. It should be a spark to ignite one’s variety of views to the problem with minimal restriction or distraction to sway ones creativity away from the norm. Multiple choice tests in mathematics may effectively discourage originality and advancement of theories by lingering around the established norms ( Pythagoras theory, Eulers theory, ….) and not allowing creative follow up and meaningful advancement or critique of the said norms.
When will mathematics be viewed as it should: a very cognitively nourishing spectrum of opportunities and a way to overcome many life puzzles? This cannot be the view if one is bound by perhaps faulty imaginations of another party in the name of the examiner. Mathematics should be a liberating rather than an enslaving and thought restricting discipline. It should be a bedrock of scientific disciplines as well as arts by setting the mind free to manipulate ideas and prove results. This encourages innovation and adventure and is a recipe for industrial revolution in any economy.
Whereas options may crop up in life, certainly not in all instances and when they do, first the liberal mind is the best to get the most appropriate option. Assessment should therefore encourage independence of thought in consideration of other people’s findings and not bind the learner in the perhaps shallow confines of the one or few persons’ setting the questions and devising the possible options. It should spark or rather elicit a rich response or opinion of the learner allowing him/her to believe in oneself and defend one’s stand point.
Multiple choice tests should rarely be used in summative evaluation unless in a very minimal extent.
26 December, 2011 at 7:41 pm
Interesting and Must Read Papers and Articles in Mathematics | MY DIGITAL NOTEBOOK
[…] Multiple Choice Questions in Mathematics https://terrytao.wordpress.com/2008/12/14/on-multiple-choice-questions-in-mathematics/ Terence […]
21 February, 2012 at 5:15 am
Rex
The link to the “Princess Bride” video is defunct.
[Updated, thanks – T.]
28 June, 2013 at 10:22 am
mathtuition88
Reblogged this on Singapore Maths Tuition.
17 January, 2014 at 11:42 pm
Anonymous
I want to take a test as soon as possible…………i’m ready for it.
22 February, 2014 at 8:15 am
rajbala
k somewhat confusing; if it would have been in easy language it would be realy intresting
18 October, 2014 at 12:24 am
Multiple Choice Questions For Visual Art Test For 3rd Grade | News Latest Update
[…] #, #, […]
13 November, 2015 at 3:05 am
Anonymous
hi! I am MORWO lIKINJIYE FROM TANZANIA. I AM INTRESTED WITH THE DESCRIPTION ABOUT MULTIPLE CHOICE IN MATHEMATICS GIVEN ON THIS PAGE. PLEASE CAN I GET A MORE ACADEMIC ARTICLE CONTAINING THE EXPLANATIONS ABOVE? KINDLY HELP A MY RESEARCH ON MULTIPLE CHOICE IN MATHEMATICS.
MY EMAIL IS grmorwo@outlook.com
22 December, 2018 at 7:37 am
How Craig Barton wishes he’d taught maths | Gowers's Weblog
[…] Terence Tao has created a number of multiple-choice quizzes on university-level topics. He has also blogged about it here. They are not exactly diagnostic in the sense Barton is talking about, but one could imagine trying […]
9 February, 2019 at 9:44 am
How Craig Barton wishes he’d taught maths
[…] Terence Tao has created a number of multiple-choice quizzes on university-level topics. He has also blogged about it here. They are not exactly diagnostic in the sense Barton is talking about, but one could imagine trying […]
9 February, 2019 at 10:21 am
How Craig Barton wishes he’d taught maths – gutuka
[…] Terence Tao has created a number of multiple-choice quizzes on university-level topics. He has also blogged about it here. They are not exactly diagnostic in the sense Barton is talking about, but one could imagine trying […]