A normed vector space automatically generates a topology, known as the norm topology or strong topology on
, generated by the open balls
. A sequence
in such a space converges strongly (or converges in norm) to a limit
if and only if
as
. This is the topology we have implicitly been using in our previous discussion of normed vector spaces.
However, in some cases it is useful to work in topologies on vector spaces that are weaker than a norm topology. One reason for this is that many important modes of convergence, such as pointwise convergence, convergence in measure, smooth convergence, or convergence on compact subsets, are not captured by a norm topology, and so it is useful to have a more general theory of topological vector spaces that contains these modes. Another reason (of particular importance in PDE) is that the norm topology on infinite-dimensional spaces is so strong that very few sets are compact or pre-compact in these topologies, making it difficult to apply compactness methods in these topologies. Instead, one often first works in a weaker topology, in which compactness is easier to establish, and then somehow upgrades any weakly convergent sequences obtained via compactness to stronger modes of convergence (or alternatively, one abandons strong convergence and exploits the weak convergence directly). Two basic weak topologies for this purpose are the weak topology on a normed vector space , and the weak* topology on a dual vector space
. Compactness in the latter topology is usually obtained from the Banach-Alaoglu theorem (and its sequential counterpart), which will be a quick consequence of the Tychonoff theorem (and its sequential counterpart) from the previous lecture.
The strong and weak topologies on normed vector spaces also have analogues for the space of bounded linear operators from
to
, thus supplementing the operator norm topology on that space with two weaker topologies, which (somewhat confusingly) are named the strong operator topology and the weak operator topology.
— 1. Topological vector spaces —
We begin with the definition of a topological vector space, which is a space with suitably compatible topological and vector space structures on it.
Definition 1 A topological vector space
is a real or complex vector space
, together with a topology
such that the addition operation
and the scalar multiplication operation
or
is jointly continuous in both variables (thus, for instance,
is continuous from
with the product topology to
).
It is an easy consequence of the definitions that the translation maps for
and the dilation maps
for non-zero scalars
are homeomorphisms on
; thus for instance the translation or dilation of an open set (or a closed set, a compact set, etc.) is open (resp. closed, compact, etc.). We also have the usual limit laws: if
and
in a topological vector space, then
, and if
in the field of scalars, then
. (Note how we need joint continuity here; if we only had continuity in the individual variables, we could only conclude that
(for instance) if one of
or
was constant.)
We now give some basic examples of topological vector spaces.
Exercise 1 Show that every normed vector space is a topological vector space, using the balls
as the base for the topology. Show that the same statement holds if the vector space is quasi-normed rather than normed.
Exercise 2 Every semi-normed vector space is a topological vector space, again using the balls
as a base for the topology. This topology is Hausdorff if and only if the semi-norm is a norm.
Example 1 Any linear subspace of a topological vector space is again a topological vector space (with the induced topology).
Exercise 3 Let
be a vector space, and let
be a (possibly infinite) family of topologies on
, each of which turning
into a topological vector space. Let
be the topology generated by
(i.e. it is the weakest topology that contains all of the
. Show that
is also a topological vector space. Also show that a sequence
converges to a limit
in
if and only if
in
for all
. (The same statement also holds if sequences are replaced by nets.) In particular, by Exercise 2, we can talk about the topological vector space
generated by a family of semi-norms
on
.
Exercise 4 Let
be a linear map between vector spaces. Suppose that we give
the topology induced by a family of semi-norms
, and
the topology induced by a family of semi-norms
. Show that
is continuous if and only if, for each
, there exists a finite subset
of
and a constant
such that
for all
.
Example 2 (Pointwise convergence) Let
be a set, and let
be the space of complex-valued functions
; this is a complex vector space. Each point
gives rise to a seminorm
. The topology generated by all of these seminorms is the topology of pointwise convergence on
(and is also the product topology on this space); a sequence
converges to
in this topology if and only if it converges pointwise. Note that if
has more than one point, then none of the semi-norms individually generate a Hausdorff topology, but when combined together, they do.
Example 3 (Uniform convergence) Let
be a topological space, and let
be the space of complex-valued continuous functions
. If
is not compact, then one does not expect functions in
to be bounded in general, and so the sup norm does not necessarily make
into a normed vector space. Nevertheless, one can still define “balls”
in
by
and verify that these form a base for a topological structure on the vector space, although it is not quite a topological vector space structure because multiplication is no longer continuous. A sequence
converges in this topology to a limit
if and only if
converges uniformly to
, thus
is finite for sufficiently large
and converges to zero as
.
Example 4 (Uniform convergence on compact sets) Let
and
be as in the previous example. For every compact subset
of
, we can define a seminorm
on
by
. The topology generated by all of these seminorms (as
ranges over all compact subsets of
) is called the topology of uniform convergence on compact sets; it is stronger than the topology of poitnwise convergence but weaker than the topology of uniform convergence. Indeed, a sequence
converges to
in this topology if and only if
converges uniformly to
on each compact set.
Exercise 5 Show that an arbitrary product of topological vector spaces (endowed with the product topology) is again a topological vector space. [I am not sure if the same statement is true for the box topology; I believe it is false.]
Exercise 6 Show that a topological vector space is Hausdorff if and only if the origin
is closed. (Hint: first use the continuity of addition to prove the lemma that if
is an open neighbourhood of
, then there exists another open neighbourhood
of
such that
, i.e.
for all
.)
Example 5 (Smooth convergence) Let
be the space of smooth functions
. One can define the
norm on this space for any non-negative integer
by the formula
where
is the
derivative of
. The topology generated by all the
norms for
is the smooth topology: a sequence
converges in this topology to a limit
if
converges uniformly to
for each
.
Exercise 7 (Convergence in measure) Let
be a measure space, and let
be the space of measurable functions
. Show that the sets
for
,
,
form the base for a topology that turns
into a topological vector space, and that a sequence
converges to a limit
in this topology if and only if it converges in measure.
Exercise 8 Let
be given the usual Lebesgue measure. Show that the vector space
cannot be given a topological vector space structure in which a sequence
converges to
in this topology if and only if it converges almost everywhere. (Hint: construct a sequence
in
which does not converge pointwise a.e. to zero, but such that every subsequence has a further subsequence that converges a.e. to zero, and use Exercise 7′ from Notes 8.) Thus almost everywhere convergence is not “topologisable” in general.
Exercise 9 (Algebraic topology) Recall that a subset
of a real vector space
is algebraically open if the sets
are open for all
.
- (i) Show that any set which is open in a topological vector space, is also algebraically open.
- (ii) Give an example of a set in
which is algebraically open, but not open in the usual topology. (Hint: a line intersects the unit circle in at most two points.)
- (iii) Show that the collection of algebraically open sets in
is a topology.
- (iv) Show that the collection of algebraically open sets in
does not give
the structure of a topological vector space.
Exercise 10 (Quotient topology) Let
be a topological vector space, and let
be a subspace of
. Let
be the space of cosets of
; this is a vector space. Let
be the coset map
. Show that the collection of sets
such that
is open gives
the structure of a topological vector space. If
is Hausdorff, show that
is Hausdorff if and only if
is closed in
.
Some (but not all) of the concepts that are definable for normed vector spaces, are also definable for the more general category of topological vector spaces. For instance, even though there is no metric structure, one can still define the notion of a Cauchy sequence in a topological vector space: this is a sequence such that
as
(or more precisely, for any open neighbourhood
of
, there exists
such that
for all
). It is then possible to talk about a topological vector space being complete (i.e. every Cauchy sequence converges). (From a more abstract perspective, the reason we can define notions such as completeness is because a topological vector space has something better than a topological structure, namely a uniform structure.)
Remark 1 As we have seen in previous lectures, complete normed vector spaces (i.e. Banach spaces) enjoy some very nice properties. Some of these properties (e.g. the uniform boundedness principle and the open mapping theorem extend to a slightly larger class of complete topological vector spaces, namely the Fréchet spaces. A Fréchet space is a complete Hausdorff topological vector space whose topology is generated by an at most countable family of semi-norms; examples include the space
from Exercise 5 or the uniform convergence on compact sets topology from Exercise 4 in the case when
is
-compact. We will however not study Fréchet spaces systematically here.
One can also extend the notion of a dual space from normed vector spaces to topological vector spaces in the obvious manner: the dual space
of a topological space is the space of continuous linear functionals from
to the field of scalars (either
or
, depending on whether
is a real or complex vector space). This is clearly a vector space. Unfortunately, in the absence of a norm on
, one cannot define the analogue of the norm topology on
; but as we shall see below, there are some weaker topologies that one can still place on this dual space.
— 2. Compactness in the strong topology —
We now return to normed vector spaces, and briefly discuss compactness in the strong (or norm) topology on such spaces. In finite dimensions, the Heine-Borel theorem tells us that a set is compact if and only if it is closed and bounded. In infinite dimensions, this is not enough, for two reasons. Firstly, compact sets need to be complete, so we are only likely to find many compact sets when the ambient normed vector space is also complete (i.e. it is a Banach space). Secondly, compact sets need to be totally bounded, rather than merely bounded, and this is quite a stringent condition. Indeed it forces compact sets to be “almost finite-dimensional” in the following sense:
Exercise 11 Let
be a subset of a Banach space
. Show that the following are equivalent:
- (i)
is compact.
- (ii)
is sequentially compact.
- (iii)
is closed and bounded, and for every
,
lies in the
-neighbourhood
of a finite-dimensional subspace
of
.
Suppose furthermore that there is a nested sequence
of finite-dimensional subspaces of
such that
is dense. Show that the following statement is equivalent to the first three:
- (iv)
is closed and bounded, and for every
there exists an
such that
lies in the
-neighbourhood of
.
Example 6 Let
. In order for a set
to be compact in the strong topology, it needs to be closed and bounded, and also uniformly
-power integrable at spatial infinity in the sense that for every
there exists
such that
for all
. Thus, for instance, the “moving bump” example
, where
is the sequence which equals
on
and zero elsewhere, is not uniformly
power integrable and thus not a compact subset of
, despite being closed and bounded.
For “continuous”
spaces, such as
, uniform integrability at spatial infinity is not sufficient to force compactness in the strong topology; one also needs some uniform integrability at very fine scales, which can be described using harmonic analysis tools such as the Fourier transform. We will not discuss this topic here.
Exercise 12 Let
be a normed vector space.
- If
is a finite-dimensional subspace of
, and
, show that there exists
such that
for all
. Give an example to show that
is not necessarily unique (in contrast to the situation with Hilbert spaces).
- If
is a finite-dimensional proper subspace of
, show that there exists
with
such that
for all
. (cf. the Riesz lemma.)
- Show that the closed unit ball
is compact in the strong topology if and only if
is finite-dimensional.
— 3. The weak and weak* topologies —
Let be a topological vector space. Then, as discussed above, we have the vector space
of continuous linear functionals on
. We can use this dual space to create two useful topologies, the weak topology on
and the weak* topology on
:
Definition 2 (Weak and weak* topologies) Let
be a topological vector space, and let
be its dual.
- The weak topology on
is the topology generated by the seminorms
for all
.
- The weak* topology on
is the topology generated by the seminorms
for all
.
Remark 2 It is possible for two non-isomorphic topological vector spaces to have isomorphic duals, but with non-isomorphic weak* topologies. (For instance,
has a very large number of preduals, which can generate a number of different weak* topologies on
.) So, technically, one cannot talk about the weak* topology on a dual space
, without specifying exactly what the predual space
is. However, in practice, the predual space is usually clear from context.
Exercise 13 Show that the weak topology on
is a topological vector space structure on
that is weaker than the strong topology on
. Also, if
(and hence
and
) are normed vector spaces, show that the weak* topology on
is a topological vector space structure on
that is weaker than the weak topology on
(which is defined using the double dual
. When
is a reflexive normed vector space, show that the weak and weak* topologies on
are equivalent.
From the definition, we see that a sequence converges in the weak topology, or converges weakly for short, to a limit
if and only if
for all
. This weak convergence is often denoted
, to distinguish it from strong convergence
. Similarly, a sequence
converges in the weak* topology to
if
for all
(thus
, viewed as a function on
, converges pointwise to
).
Remark 3 If
is a Hilbert space, then from the Riesz representation theorem for Hilbert spaces we see that a sequence
converges weakly (or in the weak* sense) to a limit
if and only if
for all
.
Exercise 14 Show that if
is a normed vector space, then the weak topology on
and the weak* topology on
are both Hausdorff. (Hint: You will need the Hahn-Banach theorem.) In particular, we conclude the important fact that weak and weak* limits, when they exist, are unique.
The following exercise shows that the strong, weak, and weak* topologies can all differ from each other.
Exercise 15 Let
, thus
and
. Let
be the standard basis of either
,
, or
.
- Show that the sequence
converges weakly in
to zero, but does not converge strongly in
.
- Show that the sequence
converges in the weak* sense in
to zero, but does not converge in the weak or strong senses in
.
- Show that the sequence
for
converges in the weak* topology of
to zero, but does not converge in the weak or strong senses. (Hint: use a generalised limit functional).
Remark 4 Recall from Exercise 11 of Notes 9 that sequences in
which converge in the weak topology, also converge in the strong topology. We caution however that the two topologies are not quite equivalent; for instance, the open unit ball in
is open in the strong topology, but not in the weak.
Exercise 16 Let
be a normed vector space, and let
be a subset of
. Show that the following are equivalent:
is strongly bounded (i.e.
is contained in a ball).
is weakly bounded (i.e.
is bounded for all
).
(Hint: use the Hahn-Banach theorem and the uniform boundedness principle.) Similarly, if
is a subset of
, and
is a Banach space, show that
is strongly bounded if and only if
is weak* bounded (i.e.
is bounded for each
).) Conclude in particular that any sequence which is weakly convergent in
or weak* convergent in
is necessarily bounded.
Exercise 17 Let
be a Banach space, and let
converge weakly to a limit
. Show that the sequence
is bounded, and
Observe from Exercise 15 that strict inequality can hold (cf. Fatou’s lemma). Similarly, if
converges in the weak* topology to a limit
, show that the sequence
is bounded and that
Again, construct an example to show that strict inequality can hold. Thus we see that weak or weak* limits can lose mass in the limit, as opposed to strong limits (note from the triangle inequality that if
converges strongly to
, then
converges to
).
Exercise 18 Let
be a Hilbert space, and let
converge weakly to a limit
. Show that the following statements are equivalent:
converges strongly to
.
converges to
.
Exercise 19 Let
be a separable Hilbert space. We say that a sequence
converges in the Césaro sense to a limit
if
converges strongly to
as
.
- Show that if
converges strongly to
, then it also converges in the Césaro sense to
.
- Give examples to show that weak convergence does not imply Césaro convergence, and vice versa. On the other hand, if a sequence
converges both weakly and in the Césaro sense, show that the weak limit is necessarily equal to the Césaro limit.
- Show that a sequence
converges weakly to
if and only if every subsequence has a further subsequence that converges in the Césaro sense to
.
Exercise 20 Let
be a Banach space. Show that the closed unit ball in
is also closed in the weak topology, and the closed unit ball in
is closed in the weak* topology.
Exercise 21 Let
be a Banach space. Show that the weak* topology on
is complete.
Exercise 22 Let
be a normed vector space, let
be a subspace of
which is closed in the strong topology of
.
- Show that
is closed in the weak topology of
.
- If
is a sequence and
, show that
converges to
in the weak topology of
if and only if it converges to
in the weak topology of
. (Because of this fact, we can often refer to “the weak topology” without specifying the ambient space precisely.)
Exercise 23 Let
with the uniform (i.e.
) norm, and identify the dual space
with
in the usual manner.
- Show that a sequence
converges weakly to a limit
if and only if the
are bounded in
and converge pointwise to
.
- Show that a sequence
converges in the weak* topology to a limit
if and only if the
are bounded in
and converge pointwise to
.
- Show that the weak topology in
is not complete.
(More generally, it may help to think of the weak and weak* topologies as being analogous to pointwise convergence topologies.)
One of the main reasons why we use the weak and weak* topologies in the first place is that they have much better compactness properties than the strong topology, thanks to the Banach-Alaoglu theorem:
Theorem 3 (Banach-Alaoglu theorem) Let
be a normed vector space. Then the closed unit ball of
is compact in the weak* topology.
This result should be contrasted with Exercise 12.
Proof: Let’s say is a complex vector space (the case of real vector spaces is of course analogous). Let
be the closed unit ball of
, then any linear functional
maps the closed unit ball
of
into the disk
. Thus one can identify
with a subset of
, the space of functions from
to
. One easily verifies that the weak* topology on
is nothing more than the product topology of
restricted to
. Also, one easily shows that
is closed in
. But by Tychonoff’s theorem,
is compact, and so
is compact also.
One should caution that the Banach-Alaoglu theorem does not imply that the space is locally compact in the weak* topology, because the norm ball in
has empty interior in the weak* topology unless
is finite dimensional. In fact, we have the following result of Riesz:
Exercise 24 Let
be a locally compact Hausdorff topological vector space. Show that
is finite dimensional. (Hint: If
is locally compact, then there exists an open neighbourhood
of the origin whose closure is compact. Show that
for some finite-dimensional subspace
, where
. Iterate this to conclude that
for any
. On the other hand, use the compactness of
to show that for any point
there exists
such that
is disjoint from
. Conclude that
and thence that
.)
The sequential version of the Banach-Alaoglu theorem is also of importance (particularly in PDE):
Theorem 4 (Sequential Banach-Alaoglu theorem) Let
be a separable normed vector space. Then the closed unit ball of
is sequentially compact in the weak* topology.
Proof: The functionals in are uniformly bounded and uniformly equicontinuous on
, which by hypothesis has a countable dense subset
. By the sequential Tychonoff theorem, any sequence in
then has a subsequence which converges pointwise on
, and thus converges pointwise on
by Exercise 28 of Notes 10, and thus converges in the weak* topology. But as
is closed in this topology, we conclude that
is sequentially compact as required.
Remark 5 One can also deduce the sequential Banach-Alaoglu theorem from the general Banach-Alaoglu theorem by observing that the weak* topology on (bounded subsets of) the dual of a separable space is metrisable. The sequential Banach-Alaoglu theorem can break down for non-separable spaces. For instance, the closed unit ball in
is not sequentially compact in the weak* topology, basically because the space
of ultrafilters is not sequentially compact (see Exercise 12 of these lecture notes).
If is reflexive, then the weak topology on
is identical to the weak* topology on
. We thus have
Corollary 5 If
is a reflexive normed vector space, then the closed unit ball in
is weakly compact, and (if
is separable) is also sequentially weakly compact.
Remark 6 If
is a normed vector space that is not separable, then one can show that
is not separable either. Indeed, using transfinite induction on first uncountable ordinal, one can construct an uncountable proper well-ordered chain of closed separable subspaces of the inseparable space
, which by the Hahn-Banach theorem induces an uncountable proper well-ordered chain of closed subspaces on
, which is not compatible with separability. As a consequence, a reflexive space is separable if and only if its dual is separable. [On the other hand, separable spaces can have non-separable duals; consider
, for instance.]
In particular, any bounded sequence in a reflexive separable normed vector space has a weakly convergent subsequence. This fact leads to the very useful weak compactness method in PDE and calculus of variations, in which a solution to a PDE or variational problem is constructed by first constructing a bounded sequence of “near-solutions” or “near-extremisers” to the PDE or variational problem, and then extracting a weak limit. However, it is important to caution that weak compactness can fail for non-reflexive spaces; indeed, for such spaces the closed unit ball in may not even be weakly complete, let alone weakly compact, as already seen in Exercise 23. Thus, one should be cautious when applying the weak compactness method to a non-reflexive space such as
or
. (On the other hand, weak* compactness does not need reflexivity, and is thus safer to use in such cases.)
In later notes we will see that the (sequential) Banach-Alaoglu theorem will combine very nicely with the Riesz representation theorem for measures, leading in particular to Prokhorov’s theorem.
— 4. The strong and weak operator topologies —
Now we turn our attention from function spaces to spaces of operators. Recall that if and
are normed vector spaces, then
is the space of bounded linear transformations from
to
. This is a normed vector space with the operator norm
This norm induces the operator norm topology on . Unfortunately, this topology is so strong that it is difficult for a sequence of operators
to converge to a limit; for this reason, we introduce two weaker topologies.
Definition 6 (Strong and weak operator topologies) Let
be normed vector spaces. The strong operator topology on
is the topology induced by the seminorms
for all
. The weak operator topology on
is the topology induced by the seminorms
for all
and
.
Note that a sequence converges in the strong operator topology to a limit
if and only if
strongly in
for all
, and
converges in the weak operator topology. (In contrast,
converges to
in the operator norm topology if and only if
converges to
uniformly on bounded sets.) One easily sees that the weak operator topology is weaker than the strong operator topology, which in turn is (somewhat confusingly) weaker than the operator norm topology.
Example 7 When
is the scalar field, then
is canonically isomorphic to
. In this case, the operator norm and strong operator topology coincide with the strong topology on
, and the weak operator norm topology coincides with the weak topology on
. Meanwhile,
coincides with
, and the operator norm topology coincides with the strong topology on
, while the strong and weak operator topologies correspond with the weak* topology on
.
We can rephrase the uniform boundedness principle for convergence (Corollary 1 from Notes 9) as follows:
Proposition 7 (Uniform boundedness principle) Let
be a sequence of bounded linear operators from a Banach space
to a normed vector space
, let
be another bounded linear operator, and let
be a dense subspace of
. Then the following are equivalent:
converges in the strong operator topology of
to
.
is bounded in the operator norm (i.e.
is bounded), and the restriction of
to
converges in the strong operator topology of
to the restriction of
to
.
Exercise 25 Show that the conclusion of Proposition 7 continues to hold if “strong operator topology” is replaced by “weak operator topology” throughout.
Exercise 26 Show that the operator norm topology, strong operator topology, and weak operator topology, are all Hausdorff. As these topologies are nested, we thus conclude that it is not possible for a sequence of operators to converge to one limit in one of these topologies and to converge to a different limit in another.
Example 8 Let
, and for each
, let
be the translation operator by
:
. If
is continuous and compactly supported, then (e.g. from dominated convergence) we see that
in
as
. Since the space of continuous and compactly supported functions is dense in
, this implies (from the above proposition, with some obvious modifications to deal with the continuous parameter
instead of the discrete parameter
) that
converges in the strong operator topology (and hence weak operator topology) to the identity. On the other hand,
does not converge to the identity in the operator norm topology. Indeed, observe for any
that
, and thus
.
In a similar vein,
does not converge to anything in the strong operator topology (and hence does not converge in the operator norm topology either) in the limit
, since
(say) does not converge strongly in
. However, one easily verifies that
as
for any compactly supported
, and hence for all
by the usual limiting argument, and hence
converges in the weak operator topology to zero.
The following exercise may help clarify the relationship between the operator norm, strong operator, and weak operator topologies.
Exercise 27 Let
be a Hilbert space, and let
be a sequence of bounded linear operators.
- Show that
in the operator norm topology if and only if
for any bounded sequences
.
- Show that
in the strong operator topology if and only if
for any convergent sequence
and any bounded sequence
.
- Show that
in the weak operator topology if and only if
for any convergent sequences
.
- Show that
in the operator norm (resp. weak operator) topology if and only if
in the operator norm (resp. weak operator) topology. Give an example to show that the corresponding claim for the strong operator topology is false.
There is a counterpart of the Banach-Alaoglu theorem (and its sequential analogue), at least in the case of Hilbert spaces:
Exercise 28 Let
be Hilbert spaces. Show that the closed unit ball (in the operator norm) in
is compact in the weak operator topology. If
and
are separable, show that
is sequentially compact in the weak operator topology.
The behaviour of convergence in various topologies with respect to composition is somewhat complicated, as the following exercise shows.
Exercise 29 Let
be a Hilbert space, let
be sequences of operators, and let
be another operator.
- If
in the operator norm (resp. strong operator or weak operator) topology, show that
and
in the operator norm (resp. strong operator or weak operator) topology.
- If
in the operator norm topology, and
is bounded in the operator norm topology, show that
and
in the operator norm topology.
- If
in the strong operator topology, and
is bounded in the operator norm topology, show that
in the strong operator norm topology.
- Give an example where
in the strong operator topology, and
in the weak operator topology, but
does not converge to zero even in the weak operator topology.
Exercise 30 Let
be a Hilbert space. An operator
is said to be finite rank if its image
is finite dimensional.
is said to be compact if the image of the unit ball is precompact. Let
denote the space of compact operators on
.
- Show that
is compact if and only if it is the limit of finite rank operators in the operator norm topology. Conclude in particular that
is a closed subset of
in the operator norm topology.
- Show that an operator
is compact if and only if
is compact.
- If
is separable, show that every
is the limit of finite rank operators in the strong operator topology.
- If
, show that
maps weakly convergent sequences to strongly convergent sequences. (This property is known as complete continuity.)
- Show that
is a subspace of
, which is closed with respect to left and right multiplication by elements of
. (In other words, the space of compact operators is an two-ideal in the algebra of bounded operators.)
The weak operator topology plays a particularly important role on the theory of von Neumann algebras, which we will not discuss here. We will return to the study of compact operators next quarter, when we discuss the spectral theorem.
[Update, Feb 23: Corrections, another exercise and remark added (note renumbering).]

131 comments
Comments feed for this article
26 February, 2017 at 6:58 am
Variational methods and Weak Topologies: Part 1 | Knowing the odds
[…] NLS in this post, for the readers interested in a deep understading in the subject we suggest this Terence Tao’s post or the third chapter of Brezis’ book. Our main interest here is to present a version of a […]
17 April, 2017 at 3:32 pm
keej
Regarding this comment in Remark 5: “…the weak* topology on the dual of a separable space is metrisable.” This is not quite true, right? Wouldn’t this imply that the weak topology on every separable Hilbert space is metrizable? [Yes, this is a special case of Remark 5. -T.]
19 April, 2017 at 11:11 pm
keej
Dear Professor Tao, thanks for your reply, but I am still confused… I should have mentioned this in the original comment, but I think a well-known example is the set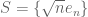 in a Hilbert space with countably infinite basis
in a Hilbert space with countably infinite basis  . The weak closure of
. The weak closure of  contains
contains 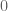 , but no sequence in
, but no sequence in  converges to
converges to 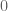 . So the weak topology cannot be metrizable. Am I still making a mistake somewhere?
. So the weak topology cannot be metrizable. Am I still making a mistake somewhere?
20 April, 2017 at 2:08 pm
Terence Tao
Ah, I see the issue now. It is the bounded subsets of a normed vector space with the weak* topology that are metrisable; as you point out, unbounded sets need not be metrisable. (This was fixed in the published version of these notes, but not in this blog post, but I will correct this now.)
13 June, 2018 at 12:32 am
Mike Neely
In Exercise 16, should “completeness” be added? Else we can
define V as the set of all real-valued infinite sequences with a finite
number of nonzero entries, define ||x||^2=sum_{i=1}^{\infty} x_i^2,
and E = {(1,0,0,…), (0,1,0,0…), (0,0,1,0,…), …} which is strongly
bounded but not weakly.
13 June, 2018 at 9:51 am
Terence Tao
All strongly bounded sets are weakly bounded (note that linear functionals in the dual space are, by definition, bounded – we are not referring here to the algebraic dual).
are, by definition, bounded – we are not referring here to the algebraic dual).
13 June, 2018 at 10:36 am
Mike Neely
Thanks for your reply! I likely am using “algebraic dual” unwittingly, since I don’t know another definition of V*. If we use algebraic dual, it seems E is not weakly bounded since we can consider the linear functional f:V—>R defined by mapping the basis vectors
{e_1, e_2, e_3, …} as follows: f(e_k)=k for all k in {1, 2, 3, …}.
This maps every sequence in V to a real number (since sequences
in V have at most a finite number of nonzeros). And so
f(E) = {f(e_1), f(e_2), f(e_3), …} = {1,2, 3, …}
is not a bounded set. Is this correct reasoning if we use “algebraic dual space”? The wiki page here defines “dual space” without the boundedness condition you give: https://en.wikipedia.org/wiki/Dual_space
14 June, 2018 at 7:43 am
Terence Tao
As stated in the second paragraph of the wikipedia page you link, in the category of topological vector spaces, one usually works with the continuous dual space instead of the algebraic dual space, in which the linear functional is required to be continuous (or equivalently, bounded). See also Remark 1 in the previous notes https://terrytao.wordpress.com/2009/01/26/245b-notes-6-duality-and-the-hahn-banach-theorem/ . Certainly many results in functional analysis involving the continuous dual space will break down if the algebraic dual space is used instead, and as such the latter is rarely used in this subject.
22 August, 2020 at 1:31 am
Kenneth Harris
For proposition 7, do we need Y to be complete also? Otherwise doesn’t the following counterexample hold?
https://math.stackexchange.com/questions/690326/uniform-boundedness-principle-for-norm-convergence
23 August, 2020 at 5:19 am
Kenneth Harris
Please ignore the last question! The fact that the existence of T is stated in the hypothesis rules out this as a counterexample, and means we don’t need to require Y complete.
18 October, 2020 at 6:57 am
Anonymous
In definition 1, if instead of joint continuity, one uses separate continuity, does one still has ?
?
18 October, 2020 at 7:58 am
Terence Tao
No. For instance if one gives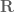 the cofinite topology then the sequences
the cofinite topology then the sequences  and
and  both converge to 0 (as well as to every other real number) but their sum does not. Granted, in this particular case scalar multiplication is also discontinuous, but one can fix this by e.g., working with an infinite-dimensional vector space
both converge to 0 (as well as to every other real number) but their sum does not. Granted, in this particular case scalar multiplication is also discontinuous, but one can fix this by e.g., working with an infinite-dimensional vector space  endowed with the topology where the non-empty open sets are the complement of subsets of finite-dimensional subspaces that are closed in the natural topology of those subspaces, and then working with
endowed with the topology where the non-empty open sets are the complement of subsets of finite-dimensional subspaces that are closed in the natural topology of those subspaces, and then working with 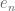 and
and  rather than
rather than  and
and  .
.
31 March, 2021 at 1:15 am
SK Rayamajhi
Regarding example 8: What about operator $T_{B_t} f(x) = f(B_t(x))$ where $B_t$ is some mapping in domain of function.
6 April, 2022 at 8:08 am
Anonymous
dear prof. Tao, in exercise 21, what does it mean to say that the weak* topology on is complete? similarly, in exercise 23, i don’t understand the statement that the weak topology in
is complete? similarly, in exercise 23, i don’t understand the statement that the weak topology in  is not complete. thank you.
is not complete. thank you.
[See https://en.wikipedia.org/wiki/Complete_topological_vector_space -T]
7 April, 2022 at 8:35 pm
Anonymous
thank you for your help! i was confused partially because the paragraph before remark 1 defined completeness in TVS using Cauchy sequences, which seems to usually be called sequential completeness in the literature. the claim in exercise 21 seems to hold for sequential completeness but not for completeness (as defined using Cauchy nets as in the Wikipedia article)
some useful links for anyone else who gets stuck here:
https://math.stackexchange.com/questions/1863811/is-x-complete-with-weak-topology
https://math.stackexchange.com/questions/3161333/on-weak-sequentially-completeness
Click to access incompleteness.pdf
31 December, 2022 at 5:45 am
Anonymous
Has a topology of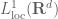 been defined somewhere in this set of notes? Maybe another good example after Example 4.
been defined somewhere in this set of notes? Maybe another good example after Example 4.
2 January, 2023 at 8:21 am
Anonymous
In Exercise 3, if for every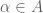 ,
, 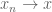 in
in 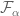 , then since
, then since 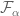 is _part_ of
is _part_ of  , it is trivial to see that
, it is trivial to see that 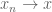 . Why is the inverse also true?
. Why is the inverse also true?  is generated by the union instead of the intersections of
is generated by the union instead of the intersections of  . Why it can’t be true that
. Why it can’t be true that 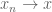 in
in  but
but 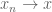 in
in  for only one
for only one  ?
?
7 January, 2023 at 7:54 am
Terence Tao
Your implications are the wrong way around: in
in  implies
implies  in
in  , but not conversely. (I recommend writing out these convergence statements explicitly using quantifiers.)
, but not conversely. (I recommend writing out these convergence statements explicitly using quantifiers.)
7 January, 2023 at 2:11 pm
Anonymous
Ah, I somehow messed up with the implications. The trivial one should be implies
implies  for every
for every  , which follows from the fact that each
, which follows from the fact that each  is part of
is part of 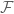 . The other direction follows from the fact that the collections of all the open sets in all
. The other direction follows from the fact that the collections of all the open sets in all  form a sub-basis of
form a sub-basis of 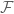 .
.
1. Suppose and
and 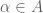 . If
. If  is any open set in
is any open set in  that contains
that contains  , then since
, then since  is also open in
is also open in 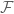 , it must contain
, it must contain 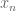 for all sufficiently large
for all sufficiently large  . This completes the trivial direction.
. This completes the trivial direction.
2. Now suppose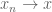 in
in  for every
for every 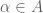 . Suppose
. Suppose  for an open set
for an open set  in
in 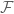 . Since
. Since 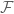 is generated by the collection
is generated by the collection  (
(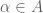 ),
),  can be written as a union of finite intersections of open sets from
can be written as a union of finite intersections of open sets from  and thus particularly,
and thus particularly, 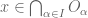 where
where 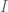 is a finite subset of
is a finite subset of  and
and 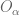 is an open set in
is an open set in  . By the assumption,
. By the assumption,  contains
contains 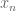 for all sufficiently large
for all sufficiently large  . The proof is done.
. The proof is done.
2 January, 2023 at 9:15 am
Anonymous
In Exercise 4, suppose for each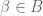 , there exists a finite subset
, there exists a finite subset 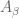 of
of  and a constant
and a constant 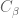 such that
such that 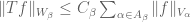 for all
for all  .
.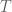 is continuous, it suffices to show that $latext T^{-1}(B)$ is open in $V$ for every
is continuous, it suffices to show that $latext T^{-1}(B)$ is open in $V$ for every 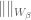 ball
ball  since the inverse
since the inverse  commutes with union and intersections and the balls form a subbasis.
commutes with union and intersections and the balls form a subbasis.
To show that
Let be a
be a 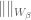 ball. One can write for some r,
ball. One can write for some r,

 ? I expect that one can use the finite set
? I expect that one can use the finite set 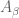 in the assumption. But I don't see how to construct the desired balls.
in the assumption. But I don't see how to construct the desired balls.
How can one write this as a union of finite intersections of balls in
7 January, 2023 at 2:24 pm
Anonymous
In Folland’s book, the author uses nets. I am wondering if one can work Exercise 4 out from basic definitions of continuity of maps between topological spaces.
Can one drop the “linear” assumption?
[Exercise 4 fails for nonlinear maps, even from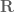 to
to 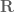 . You should be able to find a counterexample without difficulty – T.]
. You should be able to find a counterexample without difficulty – T.]
7 January, 2023 at 2:29 pm
Anonymous
Is it by default assumed that and
and  are topological vector spaces with the mentioned topologies?
are topological vector spaces with the mentioned topologies?
[This follows from the remark at the end of Exercise 3 -T.]
8 January, 2023 at 7:05 am
Anonymous
The question regarding Exercise 4 earlier was not summarized well, and I’d like to rephrase it here.
Exercise 4 is a generalization of “Lemma 1 (Continuity is equivalent to boundedness for linear operators)” in Notes 3. One can try to adapt the argument to prove Exercise 4.
The implication that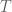 being continuous implies the inequality for seminorms seems easy using homogeneity as in “Lemma 1”:
being continuous implies the inequality for seminorms seems easy using homogeneity as in “Lemma 1”:
If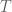 is continuous, then it is continuous at
is continuous, then it is continuous at 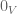 particularly. If
particularly. If  is a neighborhood of
is a neighborhood of  , then
, then  contains an open neighborhood
contains an open neighborhood  of
of 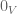 and
and  is a finite intersection of balls by the seminorms in
is a finite intersection of balls by the seminorms in  . So there exists
. So there exists 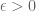 and finitely many seminorms in
and finitely many seminorms in  such that
such that


 .
.
whenever
One can then work with homogeneity as in "Lemma 1" to get
The other implication seems more tricky. Suppose the seminorm inequalit(ies) are true. Then by linearity, as in "Lemma 1", to show that is continuous, it suffices to show that
is continuous, it suffices to show that  is continuous at
is continuous at  . In order to do that, here is the question: how could one show that
. In order to do that, here is the question: how could one show that

 ? (When the finite set
? (When the finite set  contains only one element, this is rather trivial though.)
contains only one element, this is rather trivial though.)
is an open set in
12 January, 2023 at 9:44 am
Terence Tao
Each seminorm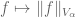 is a continuous function, so any finite sum of these seminorms is also continuous.
is a continuous function, so any finite sum of these seminorms is also continuous.
12 January, 2023 at 5:22 pm
Anonymous
Sorry, I may misunderstand your comment, but I seem to get something circular then: in order to show that any finite sum of these seminorms is also continuous in the first place, I need to show that
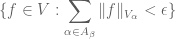
 , which what is to be proved.
, which what is to be proved.
that
is an open set in
13 January, 2023 at 6:17 am
Terence Tao
The sum of any finite number of real-valued continuous functions is automatically continuous. (This is ultimately because the addition map defined by
defined by  is continuous.)
is continuous.)
13 January, 2023 at 3:41 pm
Anonymous
If one takes two seminorms, and
and  , then in order to show the continuity of
, then in order to show the continuity of  using the continuity of the addition map of real numbers, I think I need to show first that
using the continuity of the addition map of real numbers, I think I need to show first that 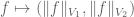 is continuous. But then I end up needing to show that the sets of the form
is continuous. But then I end up needing to show that the sets of the form
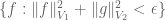
 , which is quite the same as what is to be proved… What do I miss?
, which is quite the same as what is to be proved… What do I miss?
are open in
13 January, 2023 at 7:37 pm
Anonymous
Ah, never mind. I was lost. That should follow from properties of the product topology on .
.
14 January, 2023 at 7:08 pm
Anonymous
Dr. Tao: How do you have so much patience answering such simple questions? People shouldn’t abuse this blog.
2 January, 2023 at 1:39 pm
Anonymous
Exercise 13 and Theorem 3 in Section 3 in this set of notes use the norm on . But the notion of operator norms, of which the norm on
. But the notion of operator norms, of which the norm on  is a special case, is not defined until Section 4. Do I miss anything? Was it defined or mentioned already before this set of notes?
is a special case, is not defined until Section 4. Do I miss anything? Was it defined or mentioned already before this set of notes?
[See Notes 6. -T]
15 January, 2023 at 5:12 am
Anonymous
Instead, one often first works in a weaker topology, in which compactness is easier to establish, and then somehow upgrades any weakly convergent sequences obtained via compactness to stronger modes of convergence …
In this situation, could one have worked (in principle maybe) at the very beginning directly with the stronger topologies that give the “stronger modes of convergence” by rearranging the arguments without referring to any “weak” topologies?
15 January, 2023 at 8:21 pm
Anonymous
It is usually the case that stronger topologies don’t work, then we go to weak topologies.
30 January, 2023 at 6:01 am
Anonymous
In Exercise 26, how does one know that the three topologies are nested? The chain of inequalities:
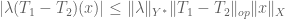

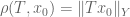 . Does this imply that the operator norm topology is finer than the strong operator topology?
. Does this imply that the operator norm topology is finer than the strong operator topology?
shows that sub-basic sets in these topologies are nested. For instance,
where
In general, if one has two topologies and
and 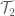 with subbases
with subbases  and
and  respectively, and if for every
respectively, and if for every 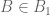 there exists
there exists 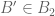 such that
such that 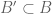 , can one conclude that
, can one conclude that  is finer than
is finer than  ?
?
30 January, 2023 at 10:57 am
Anonymous
Yes. What you wrote is correct.
1 February, 2023 at 4:46 am
Anonymous
In Exercise 10, is it less useful to define the open sets in using the forward image of open sets (in
using the forward image of open sets (in  ) under the map
) under the map  ?
?
1 February, 2023 at 9:42 am
Anonymous
We want it to be a topology, not sure what will one achieve by using the forward image of open sets.
3 February, 2023 at 7:24 pm
J
To show the continuity of addition in V/W for Exercise 10, suppose let![[v_1], [v_2]\in V/W](https://s0.wp.com/latex.php?latex=%5Bv_1%5D%2C+%5Bv_2%5D%5Cin+V%2FW&bg=ffffff&fg=545454&s=0&c=20201002) and
and  is an open set that contains
is an open set that contains ![[v_1]+[v_2]=[v_1+v_2]](https://s0.wp.com/latex.php?latex=%5Bv_1%5D%2B%5Bv_2%5D%3D%5Bv_1%2Bv_2%5D&bg=ffffff&fg=545454&s=0&c=20201002) . Then
. Then  is in the open set
is in the open set 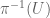 . By continuity of addition in
. By continuity of addition in  one has open sets
one has open sets  in
in  such that
such that  and
and 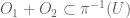 .
.
To show the continuity of the addition of V/W, one needs an open set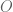 in
in  that contains
that contains ![([v_1], [v_2])](https://s0.wp.com/latex.php?latex=%28%5Bv_1%5D%2C+%5Bv_2%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) and the image of
and the image of 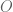 under addition is contained in
under addition is contained in  . How can one get the desired
. How can one get the desired  ?
?
3 February, 2023 at 7:29 pm
J
By chasing the maps, one can see that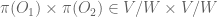 and it contains
and it contains ![([v_1],[v_2])](https://s0.wp.com/latex.php?latex=%28%5Bv_1%5D%2C%5Bv_2%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . But unfortunately, it is not necessarily open.
. But unfortunately, it is not necessarily open.
4 February, 2023 at 7:29 am
J
Okay, it seems (much) easier to work with the inverse image of open sets instead of continuity at a point. It would be interesting to see if it is possible to fix the argument above directly.
5 February, 2023 at 11:51 am
Anonymous
Can you give a hint for the implication that being Hausdorff topological vector space and
being Hausdorff topological vector space and  being a closed subspace of
being a closed subspace of  implies
implies  is Hausdorff in exercise 10? How can one construct two open sets to separate
is Hausdorff in exercise 10? How can one construct two open sets to separate ![[p]\neq [q]](https://s0.wp.com/latex.php?latex=%5Bp%5D%5Cneq+%5Bq%5D&bg=ffffff&fg=545454&s=0&c=20201002) in
in  ?
?
10 February, 2023 at 5:55 pm
Anonymous
I think I’ve figured it out: one can work out Exercise 6 first. One then uses the fact that the projection is continuous, and thus a set
is continuous, and thus a set  is closed in
is closed in  if and only if
if and only if 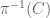 is closed in
is closed in  . Now one can let
. Now one can let  .
.
(It is rather difficult to prove the result directly from the definition of Hausdorff. One has to exploit the properties of topological vector spaces.)
8 February, 2023 at 5:42 pm
Anonymous
For Exercise 6, does one eventually also need to use the fact that the open set in the hint could be assumed in addition that
in the hint could be assumed in addition that 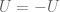 ?
?