This is a continuation of the 700-799 thread of the polymath1 project, which is now full. During the course of that thread, we have made significant progress on the three problems being focused on:
1. Upper and lower bounds for for small n.
Let be the largest size of a set in
without a combinatorial line. We now have both human and computer-assisted proofs of the first few values of this sequence:
.
The current best-known bounds for are
. Given the gap involved here, and the rate at which the complexity of the problem has increased with n, it seems unlikely that we will be able to compute
exactly any time soon, but it is possible that some improvement can still be made here.
2. A hyper-optimistic conjecture
Consider a variant of the above problem in which each element of with a 1s, b 2s, and c 3s is weighted by the factor
; this gives
a total weight of
. Let
be the largest weight of a line-free set of
, and let
be the largest size of a subset of
which contains no upward-pointing equilateral triangles with r>0. It is known that
; the “hyper-optimistic conjecture” is that one in fact has
. This would imply density Hales-Jewett for k=3.
Currently, the conjecture is verified for , where the values of
for
are 1,2,4,6,9,12 respectively; see this page and this page for details. It seems feasible to handle
. Currently we know that
and
.
3. Asymptotics for Moser’s cube problem
Moser’s cube problem asks to compute the largest size of a subset of the cube
without geometric lines. The first few values of
are known:
.
The best asymptotic lower bound known is still of the order of . Improving this bound seems related to the well-known problem of improving the bounds in Behrend’s construction of an AP-3 free set of integers.
We are quite close now to pinning down ; we know that it is equal to either 124 or 125, and it is looking increasingly unlikely that it is 125.
Comments on this thread should start at 900.

110 comments
Comments feed for this article
13 March, 2009 at 3:15 pm
Terence Tao
990. Diagonal Moser cubes
Michael, this is great! I of course plunked the inequalities into the linear program at
http://michaelnielsen.org/polymath1/index.php?title=Maple_calculations
to see what improves. The 4D bound for a+b+c+d+e+d/2 for e=1 improved from 41.5 to 40, giving a new inequality a+b+c+d+e+d/2 + 3e <= 43. The 5D bound a+b+c+d+e+f <= 119 for f=1 improved to 117, giving a new inequality a+b+c+d+e+f+7f <= 124. The bound unfortunately did not budge at 361, but the extremal changed (e and f became even smaller), suggesting that at least some of the 361-point cases were eliminated. When g=1, the bound dropped from 355 to 352, which is below Kareem’s example and thus demonstrates for the first time that g=0 for the
bound unfortunately did not budge at 361, but the extremal changed (e and f became even smaller), suggesting that at least some of the 361-point cases were eliminated. When g=1, the bound dropped from 355 to 352, which is below Kareem’s example and thus demonstrates for the first time that g=0 for the  extremiser.
extremiser.
In 7D, the bound for improved from 1078 to 1073, and when h=1 there is a further improvement from 1071 to 1065. So the new inequalities are having an impact…
improved from 1078 to 1073, and when h=1 there is a further improvement from 1071 to 1065. So the new inequalities are having an impact…
13 March, 2009 at 5:10 pm
Michael Peake
991. Diagonal Moser cubes
Inequalities arising from xxxyz diagonals:
Letters a to f are densities
8a+4b+2c+2d+4e+2f <=11
4a+2b+1c+2d+2e+1f <= 6
0a+0b+2c+0d+0e+1f <= 2
4a+4b+1c+0d+2e+1f <= 6
7a+2b+1c+1d+2e+1f <= 7
8a+2b+1c+2d+2e+1f <= 8
4a+0b+2c+0d+0e+1f <= 4
4a+0b+2c+2d+2e+1f <= 6
8a+0b+2c+2d+2e+1f <= 8
8a+4b+1c+0d+2e+1f <= 8
Inequalities arising from xxxxyz diagonals
a,b,c,e,f,g are densities. These cubes do not intersect the d slice
8a+4b+2c+2e+4f+2g <= 11
0a+0b+2c+0e+0f+1g <= 2
4a+2b+1c+2e+2f+1g <= 6
7a+2b+1c+1e+2f+1g <= 7
4a+0b+2c+0e+0f+1g <= 4
4a+0b+2c+2e+2f+1g <= 6
8a+0b+2c+2e+2f+1g <= 8
8a+2b+1c+2e+2f+1g <= 8
4a+4b+1c+0e+2f+1g <= 6
8a+4b+1c+0e+2f+1g <= 8
Inequalities from xxxyyz diagonals
Letters a to g are densities
4a+2b+0c+3d+1e+1f+1g <= 6
4a+0b+2c+3d+1e+1f+1g <= 6
8a+2b+0c+3d+1e+1f+1g <= 8
8a+0b+2c+3d+1e+1f+1g <= 8
0a+4b+0c+0d+2e+0f+1g <= 4
0a+0b+4c+0d+0e+2f+1g <= 4
8a+4b+0c+0d+2e+0f+1g <= 1
8a+0b+4c+0d+0e+2f+1g <= 1
13 March, 2009 at 8:39 pm
Terence Tao
992.
Michael, there seems to be something wrong with your third set of inequalities (xxxyyz), for instance they are inconsistent with the densities a=1, b=c=d=e=f=g=0, which is of course feasible. Perhaps the weighting is a bit off?
13 March, 2009 at 10:10 pm
Kevin O'Bryant
993. Question II.A revisited
Post 984 is a bit off, as I used in a place I should have had
in a place I should have had 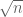 . Here’s an improved construction, with corrected analysis of its size.
. Here’s an improved construction, with corrected analysis of its size.
It comes down to this: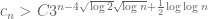 for some absolute constant
for some absolute constant  , and where all logarithms are base-3.
, and where all logarithms are base-3.
For convenience, let be a multiple of 3. Elkin’s bound gives
be a multiple of 3. Elkin’s bound gives  , and let
, and let 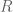 be a subset of
be a subset of  without 3-term APs and with size
without 3-term APs and with size  , and with all elements being integer multiples of 3 (again as a matter of convenience). For each
, and with all elements being integer multiples of 3 (again as a matter of convenience). For each  , let
, let  . The set
. The set  is the union of all
is the union of all  . Since all of
. Since all of 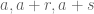 are between
are between  and
and  , the size of
, the size of  is at least
is at least 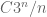 . Since there are
. Since there are 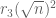 choices for
choices for  and
and  , we have a set with size at least
, we have a set with size at least
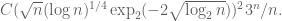
 , where
, where  , assuming my algebra holds this time.
, assuming my algebra holds this time.
This simplifies to
Now suppose that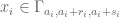 is a combinatorial line in the set
is a combinatorial line in the set  . Then
. Then 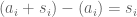 is a 3-term AP contained in
is a 3-term AP contained in 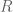 , so the
, so the 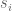 are all the same. Similarly, all of the
are all the same. Similarly, all of the  are the same, and therefore all of the
are the same, and therefore all of the  are the same, too. But this implies that the
are the same, too. But this implies that the 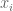 sequence is constant, which means the line is degenerate.
sequence is constant, which means the line is degenerate.
13 March, 2009 at 11:18 pm
Michael Peake
993. Moser’s diagonal cubes – correction
Hi Terry. Thanks for checking that.
The last two inequalities for xxxyyz should have 8 on the RHS.
8a+4b+0c+0d+2e+0f+1g <= 8
8a+0b+4c+0d+0e+2f+1g <= 8
The extremals for xxxyyz are
(4113111),(3223111),(2224220),(4113220),(4224200), (4223011),(4226000),(4222220),(4422020),(4224020), (4222111),(4223101),(4242200),(4444000),(8000000)
I checked the other inequalities, and I believe they are correct.
The density inequalities for xxyz, which I didn’t give above, are
4a+2b+3c+2d+e <= 6
8a+2b+3c+2d+e <= 8
14 March, 2009 at 6:04 am
Seva
994. While all the major players are (supposedly) still out there, I wonder whether anything intelligent can be said on the smallest possible size of a Kakeya set in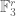 . Let’s denote it
. Let’s denote it 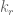 ; thus,
; thus, 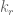 is the smallest integer for which a set
is the smallest integer for which a set  exists such that
exists such that  and for every
and for every 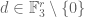 , the set
, the set 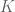 has a line in the direction
has a line in the direction  . (A line in the direction
. (A line in the direction  is, of course, a three-element set of the form
is, of course, a three-element set of the form  .)
.)
Clearly, we have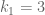 , and it is easy to see that
, and it is easy to see that  . Using a computer, I also found
. Using a computer, I also found  and
and 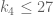 . I suspect that, indeed,
. I suspect that, indeed, 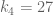 holds (meaning that in
holds (meaning that in  one cannot get away with just
one cannot get away with just 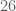 elements), and I am very curious to know whether
elements), and I am very curious to know whether  : notice the pattern in
: notice the pattern in
As to the general estimates, we have
and, on the other hand,
the former since for each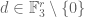 there are at least three ordered pairs of elements of a Kakeya set with difference
there are at least three ordered pairs of elements of a Kakeya set with difference  , the latter due to the fact that the set of all vectors in
, the latter due to the fact that the set of all vectors in 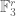 such that at least one of the numbers
such that at least one of the numbers 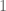 and
and 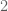 is missing among their coordinates is a Kakeya set. (I actually can improve the lower bound to something like
is missing among their coordinates is a Kakeya set. (I actually can improve the lower bound to something like 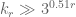 .) Also, we have the trivial inequalities
.) Also, we have the trivial inequalities
can the upper bound be strengthened to ?
?
14 March, 2009 at 8:37 am
Terence Tao
995. Thread moving
As is now our tradition, I’m declaring this thread full and am moving to the 1100-1199 thread at
I’ll try to respond to several of the interesting new comments on this thread at the other thread.
14 March, 2009 at 8:37 am
DHJ(3): 1100-1199 (Density Hales-Jewett type numbers) « What’s new
[…] March, 2009 in math.CO | Tags: polymath1 | by Terence Tao This is a continuation of the 900-999 thread of the polymath1 project, which is now full. We’ve made quite a bit of progress so far on […]