Let be two Hermitian
matrices. When
and
commute, we have the identity
When and
do not commute, the situation is more complicated; we have the Baker-Campbell-Hausdorff formula
where the infinite product here is explicit but very messy. On the other hand, taking determinants we still have the identity
Recently I learned (from Emmanuel Candes, who in turn learned it from David Gross) that there is another very nice relationship between and
, namely the Golden-Thompson inequality
The remarkable thing about this inequality is that no commutativity hypotheses whatsoever on the matrices are required. Note that the right-hand side can be rearranged using the cyclic property of trace as
; the expression inside the trace is positive definite so the right-hand side is positive. (On the other hand, there is no reason why expressions such as
need to be positive or even real, so the obvious extension of the Golden-Thompson inequality to three or more Hermitian matrices fails.) I am told that this inequality is quite useful in statistical mechanics, although I do not know the details of this.
To get a sense of how delicate the Golden-Thompson inequality is, let us expand both sides to fourth order in . The left-hand side expands as
while the right-hand side expands as
Using the cyclic property of trace , one can verify that all terms up to third order agree. Turning to the fourth order terms, one sees after expanding out
and using the cyclic property of trace as much as possible, we see that the fourth order terms almost agree, but the left-hand side contains a term
whose counterpart on the right-hand side is
. The difference between the two can be factorised (again using the cyclic property of trace) as
. Since
is skew-Hermitian,
is positive definite, and so we have proven the Golden-Thompson inequality to fourth order. (One could also have used the Cauchy-Schwarz inequality for the Frobenius norm to establish this; see below.)
Intuitively, the Golden-Thompson inequality is asserting that interactions between a pair of non-commuting Hermitian matrices are strongest when cross-interactions are kept to a minimum, so that all the
factors lie on one side of a product and all the
factors lie on the other. Indeed, this theme will be running through the proof of this inequality, to which we now turn.
The proof of the Golden-Thompson inequality relies on the somewhat magical power of the tensor power trick. For any even integer and any
matrix
(not necessarily Hermitian), we define the
-Schatten norm
of
by the formula
(This formula in fact defines a norm for any , but we will only need the even integer case here.) This norm can be viewed as a non-commutative analogue of the
norm; indeed, the
-Schatten norm of a diagonal matrix is just the
norm of the coefficients.
Note that the -Schatten norm
is the Hilbert space norm associated to the Frobenius inner product (or Hilbert-Schmidt inner product)
This is clearly a non-negative Hermitian inner product, so by the Cauchy-Schwarz inequality we conclude that
for any matrices
. As
, we conclude in particular that
We can iterate this and establish the non-commutative Hölder inequality
whenever is an even power of
. Indeed, we induct on
, the case
already having been established. If
is a power of
, then by the induction hypothesis (grouping
into
pairs) we can bound
On the other hand, we may expand
We use the cyclic property of trace to move the rightmost factor to the left. Applying the induction hypothesis again, we conclude that
But from the cyclic property of trace again, we have and
. We conclude that
and similarly for , etc. Inserting this into (3) we obtain (2).
Remark 1 Though we will not need to do so here, it is interesting to note that one can use the tensor power trick to amplify (2) for
equal to a power of two, to obtain (2) for all positive integers
, at least when the
are all Hermitian. Indeed, pick a large integer
and let
be the integer part of
. Then expand the left-hand side of (2) as
and apply (2) with
replaced by
to bound this by
. Sending
(noting that
) we obtain the claim.
Specialising (2) to the case where for some Hermitian matrices
, we conclude that
and hence by cyclic permutation
for any . Iterating this we conclude that
Applying this with replaced by
and
respectively, we obtain
Now we send . Since
and
, we have
, and so the left-hand side is
; taking the limit as
we obtain the Golden-Thompson inequality. (See also these notes of Vershynin for a slight variant of this proof.)
If we stop the iteration at an earlier point, then the same argument gives the inequality
for a power of two; one can view the original Golden-Thompson inequality as the
endpoint of this case in some sense. (In fact, the Golden-Thompson inequality is true in any operator norm; see Theorem 9.3.7 of Bhatia’s book.) In the limit
, we obtain in particular the operator norm inequality
This inequality has a nice consequence:
Corollary 2 Let
be Hermitian matrices. If
(i.e.
is positive semi-definite), then
.
Proof: Since , we have
for all vectors
, or in other words
for all
. This implies that
is a contraction, i.e.
. By (5), we conclude that
, thus
, and the claim follows.
It is not difficult to reverse the above argument and conclude that (2) is in fact equivalent to (5).
It is remarkably tricky to try to prove Corollary 2 directly. Here is a somewhat messy proof; I would be interested in seeing a more elegant argument. By the fundamental theorem of calculus, it suffices to show that whenever is a Hermitian matrix depending smoothly on a real parameter with
, then
. Indeed, Corollary 2 follows from this claim by setting
and concluding that
.
To obtain this claim, we use the Duhamel formula
This formula can be proven by Taylor expansion, or by carefully approximating by
; alternatively, one can integrate the identity
which follows from the product rule and by interchanging the and
derivatives at a key juncture. We rearrange the Duhamel formula as
Using the basic identity , we thus have
formally evaluating the integral, we obtain
and thus
As was positive semi-definite by hypothesis,
is also. It thus suffices to show that for any Hermitian
, the operator
preserves the property of being semi-definite.
Note that for any real , the operator
maps a positive semi-definite matrix
to another positive semi-definite matrix, namely
. By the Fourier inversion formula, it thus suffices to show that the kernel
is positive semi-definite in the sense that it has non-negative Fourier transform (cf. Bochner’s theorem). But a routine (but somewhat tedious) application of contour integration shows that the Fourier transform
is given by the formula
, and the claim follows.
Because of the Golden-Thompson inequality, many applications of the exponential moment method in commutative probability theory can be extended without difficulty to the non-commutative case, as was observed by Ahlswede and Winter. For instance, consider (a special case of) the Chernoff inequality
for any , where
are iid scalar random variables taking values in
of mean zero and with total variance
(i.e. each factor has variance
). We briefly sketch the standard proof of this inequality. We first use Markov’s inequality to obtain
for some parameter to be optimised later. In the scalar case, we can factor
as
and then use the iid hypothesis to write the right-hand side as
An elementary Taylor series computation then reveals the bound when
; inserting this bound and optimising in
we obtain the claim.
Now suppose that are iid
Hermitian matrices. One can try to adapt the above method to control the size of the sum
. The key point is then to bound expressions such as
As need not commute, we cannot separate the product completely. But by Golden-Thompson, we can bound this expression by
which by independence we can then factorise as
As the matrices involved are positive definite, we can then take out the final factor in operator norm:
Iterating this procedure, we can eventually obtain the bound
Combining this with the rest of the Chernoff inequality argument, we can establish a matrix generalisation
of the Chernoff inequality, under the assumption that the are iid with mean zero, have operator norm bounded by
, and have total variance
equal to
; see for instance these notes of Vershynin for details.
Further discussion of the use of the Golden-Thompson inequality and its variants to non-commutative Chernoff-type inequalities can be found in this paper of Gross, these notes of Vershynin and this recent article of Tropp. It seems that the use of this inequality may be quite useful in simplifying the proofs of several of the basic estimates in this subject.

34 comments
Comments feed for this article
15 July, 2010 at 10:29 am
Michael Nielsen
There’s a beautiful related result, due to Thompson, stating that when A and B are Hermitian, e^A e^B = e^{U A U^\dagger +V B V^\dagger}, where U and V are unitary. My memory of the proof is very hazy, but I believe it relies on Horn’s conjecture, which, of course, wasn’t proved until some years later.
See: R. C. Thompson, Linear and Multilinear Algebra 19, 187 (1986).
This result has some applications in quantum computing: http://arxiv.org/abs/quant-ph/0307190
15 July, 2010 at 10:59 am
Michael Nielsen
I believe Corollary 1 has a straightforward proof. Start by observing that it is equivalent to proving that the log function is operator monotone, i.e., A \leq B implies ln(A) \leq \ln(B) where A and B are positive definite.
There are two ideas we need: (1) the observation that the function, A -> -A^{-1} is operator monotone, when A is positive definite; and (2) an integral representation for the log function.
The proof of (1) can easily be supplied by elementary techniques. For (2), a suitable integral representation is:
\ln(A) = \int_0^1 dy / (y+(A-I)^{-1})
Assuming A \leq B we can applying (1) twice to obtain 1/(y+(A-I)^{-1}) \leq 1/(y+(B-I)^{-1}). The result then follows.
There is something wrong with this proof: (A-I) may be singular, and so the the integral representation may not exist. This can be fixed by perturbing A slightly and using a continuity argument. However, I suspect that with a slightly different integral representation that won’t be necessary. I don’t have time to fiddle with it now, unfortunately…
15 July, 2010 at 11:02 am
Terence Tao
Ah, that is a nice argument! I had forgotten that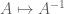 reverses the positive definite ordering, that is certainly a useful thing to keep in mind. (I was relying instead on the fact that
reverses the positive definite ordering, that is certainly a useful thing to keep in mind. (I was relying instead on the fact that  preserves positive definiteness, but this was significantly trickier to use.)
preserves positive definiteness, but this was significantly trickier to use.)
15 July, 2010 at 11:13 am
Michael Nielsen
I have a vague memory that there may even be a representation theorem for operator monotone functions in terms of integrals over inverse functions. That’s why I tried this strategy. Bhatia is most likely where I saw the result. My copy is in storage, so I can’t look it up.
20 July, 2010 at 9:49 am
Michael Nielsen
It’s bothering me that (A-I) may not be invertible, and even if it is, s+(A-I)^{-1} may not be. Anyone see a clean fix?
20 July, 2010 at 9:55 am
Terence Tao
It seems to me from the spectral theorem that there will not be an issue as long as the spectrum of A stays away from both 0 and 1, but this seems easy to ensure via a standard perturbation argument.
20 July, 2010 at 9:59 am
Michael Nielsen
If A is finite-dimensional a perturbation argument should work just fine. But if A has a spectrum dense in some interval around 0, say, then it will break down. In the context of the post (finite-dimensional matrices) I guess there’s no problem.
20 July, 2010 at 10:09 am
Terence Tao
I think there are a number of ways around this. For instance, one can first show that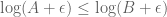 for every
for every  , and then take limits in, say, the weak operator topology. Now there is no spectrum near zero. There is still the issue of spectrum near 1, but if the operators are bounded then we can simply rescale them to have spectrum away from 1. If they are unbounded, then perhaps one can approximate them by bounded operators and take further limits.
, and then take limits in, say, the weak operator topology. Now there is no spectrum near zero. There is still the issue of spectrum near 1, but if the operators are bounded then we can simply rescale them to have spectrum away from 1. If they are unbounded, then perhaps one can approximate them by bounded operators and take further limits.
It may also be possible to deduce the infinite dimensional case from the finite dimensional case by a suitable approximation argument. Certainly I would imagine the compact case would follow fairly easily in this fashion.
19 July, 2010 at 8:05 am
Brian Davies
There is a complete and simple classification of monotone matrix functions, due to Lowner in 1934. See for example
W. F. Donoghue, Monotone matrix functions and analytic continuation. Springer-Verlag, New York, Heidelberg, Berlin, 1974
or
G Sparr: Math. Scand 47 (1980) 266-274
for a short proof.
15 July, 2010 at 12:07 pm
Ashley
Very nice post! One typo fix: “Ashwelde and Winter” should be “Ahlswede and Winter”. [Corrected, thanks – T.]
15 July, 2010 at 12:54 pm
Steve Flammia
It might be worth mentioning that the naive generalization to three matrices,
Tr(e^{A+B+C}) \le Tr(e^A e^B e^C)
is false in general. But there is a nice paper by Lieb with a nontrivial generalization:
E. Lieb, “Convex trace functions and the Wigner-Yanase-Dyson conjecture”, Advances in Mathematics, 11, 267–288 (1973).
(The generalization is at the bottom of page 282.)
14 April, 2016 at 8:25 pm
sflammia
My colleague Marco Tomamichel and his coauthors just posted a very nice paper that further generalizes the Golden-Thompson inequality, as well as Lieb’s extension to three matrices. Their result holds for n matrices, in fact, and it might be of some interest to readers of this blog post.
http://arxiv.org/abs/1604.03023
15 July, 2010 at 2:12 pm
mick
I second Ashley’s comment, a very nice post.
Also, I assume that the David Gross mentioned is the one that works in quantum information theory (ie the one that doesn’t have a Nobel prize)? More specifically, this one.
16 July, 2010 at 1:58 pm
Anonymous
Prof. Tao,
Thanks for the great posts! Is the following comment correct?
“Since![[A,B] := AB-BA](https://s0.wp.com/latex.php?latex=%5BA%2CB%5D+%3A%3D+AB-BA&bg=ffffff&fg=545454&s=0&c=20201002) is skew-Hermitian,
is skew-Hermitian, ![[A,B]^2](https://s0.wp.com/latex.php?latex=%5BA%2CB%5D%5E2+&bg=ffffff&fg=545454&s=0&c=20201002) is positive definite…”
is positive definite…”
Try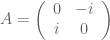 and
and  .
.
Then![[A,B] = \left( \begin{array}{cc} -4 & 0 \\ 0 & -4 \end{array} \right)](https://s0.wp.com/latex.php?latex=%5BA%2CB%5D+%3D+%5Cleft%28+%5Cbegin%7Barray%7D%7Bcc%7D+-4+%26+0++%5C%5C+0+%26+-4+%5Cend%7Barray%7D+%5Cright%29&bg=ffffff&fg=545454&s=0&c=20201002)
16 July, 2010 at 6:50 pm
Terence Tao
A factor of i is missing in your computation of the commutator [A,B].
16 July, 2010 at 9:44 pm
Anonymous
Ha! Sorry, I had intended to write:
which is not positive definite, but both A and B are hermitian.
17 July, 2010 at 9:43 am
Terence Tao
Ah, I see what happened now. Yes, there was a sign error in the original text, which has now been fixed.
17 July, 2010 at 3:09 am
Klas Markström
With the recent discussion of Cayley graphs in mind I can mention that Demetres Christofides and I used the methods of Ahlswede and Winter to prove a matrix version of Hoeffding’s concentration inequality for martingales, which we used to give an sharpened version of the Alon-Roichman theorem.
http://dx.doi.org/10.1002/rsa.20177
The Alon-Roichman theorem states that Cayley graphs based on a random subset of the group are likely to be expander graphs if the subset is large enough.
18 July, 2010 at 9:01 am
Miguel Lacruz
What follows is an elementary proof of corollary 1 in the special case that are commuting matrices. The proof uses the fact that the product of two positive definite, commuting matrices, is positive definite.
are commuting matrices. The proof uses the fact that the product of two positive definite, commuting matrices, is positive definite.
Consider the matrix valued function![A(t)=\log[(1-t)e^A+te^B]](https://s0.wp.com/latex.php?latex=A%28t%29%3D%5Clog%5B%281-t%29e%5EA%2Bte%5EB%5D&bg=ffffff&fg=545454&s=0&c=20201002) defined for every
defined for every 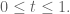 This function is differentiable and
This function is differentiable and ![A^\prime(t)=[(1-t)A+tB]^{-1} \cdot (e^B-e^A)](https://s0.wp.com/latex.php?latex=A%5E%5Cprime%28t%29%3D%5B%281-t%29A%2BtB%5D%5E%7B-1%7D+%5Ccdot+%28e%5EB-e%5EA%29&bg=ffffff&fg=545454&s=0&c=20201002) is positive definite because it is the product of two positive definite commuting matrices. Finally, take a vector
is positive definite because it is the product of two positive definite commuting matrices. Finally, take a vector 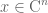 and apply the mean value theorem to find some real number
and apply the mean value theorem to find some real number  such that
such that 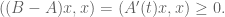
19 July, 2010 at 3:34 am
Miguel Lacruz
Your proof of corollary 1 in case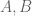 commute does not need the Golden-Thompson inequality, because then
commute does not need the Golden-Thompson inequality, because then  This is simpler than what I mentioned above.
This is simpler than what I mentioned above.
18 July, 2010 at 11:25 am
Anders Karlsson
Dear Terry,
These types of inequalities express that the exponential mapping (in the sense of differential geometry) is distance (semi)increasing, which is the source of nonpositive curvature for symmetric spaces of non-compact type. If I don’t misremember one version of the Golden-Thompson is used in one of the standard proofs (see Lang’s Fundamentals of Differential Geometry; going back to Mostow) that GLnR/OnR has nonpositive curvature.
I believe that the related inequality (5) for operators is called Segal’s inequality and is again a source of nonpositive curvature (in a weaker sense, because the tangent space is not a Hilbert space) for infinite dimensional symmetric spaces, see Gorach, G.; Porta, H.; Recht, L. A geometric interpretation of Segal’s inequality $\Vert e^{X+Y}\Vert \leq\Vert e^{X/2}e^Ye^{X/2}\Vert $. Proc. Amer. Math. Soc. 115 (1992), no. 1, 229–231, and some of their other papers.
As always, thanks for an excellent blog,
Anders
20 July, 2010 at 9:40 am
Denes PETZ
I proved in 1994 that equality in the Golden-Thompson inequality if and only if the two matrices commute. ( D. Petz, A survey of trace inequalities, in Functional Analysis and Operator Theory, 287-298, Banach Center Publications, 30 (Warszawa 1994). )
29 July, 2010 at 7:27 pm
percy deift
Dear Terry,
I have some comments regarding your blog on the Golden-Thompson inequalities that may
be of interest.
First one may ask the following quantum-mechanical-type question: For linear operators
 and
and  ,
,
if one “knows”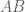 , how much does one know about
, how much does one know about  ?
?
I believe that the best one can do is given by the following:
(1)
with its quantitative version
(2)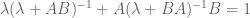
(1)(2) have many and varied applications in scattering theory, spectral theory, and
and  can even be unbounded
can even be unbounded
soliton theory, …( see e.g. my paper in the Duke Math Journal (1978) “On a commutation
formula”), and also random matrix theory. Over the last 30 years, every 2 or 3 months,
a new application of “commutation” seems to come up.
operators.
Here’s how it works for the simplest GT inequality
(3)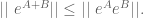
I restrict to the bounded (self-adjoint) operator case for simplicity. Let denote the spectral radius of an operator
denote the spectral radius of an operator 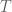 : we have
: we have
(4)
Using self-adjointness, (4), commutation, and the fact that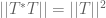 , we have
, we have
Replacing with
with 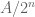 ,
,  with
with 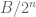 , and
, and 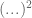 with
with 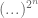 , shows that
, shows that
is decreasing with . Inequality (3) now follows by the Trotter product formula.
. Inequality (3) now follows by the Trotter product formula.
A proof of
(5)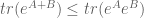
using commutation is in Reed-Simon IV. Whereas (3) only uses information about the top of the spectrum,
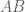 is the same as the algebraic multiplicity of
is the same as the algebraic multiplicity of  in
in 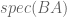 . This fact also follows from (2).
. This fact also follows from (2).
the commutation proof of (5) uses the fact that the (algebraic) multiplicity of an eigenvalue
of
Concerning the result
it is clearly enough to show that
(5) implies
implies 
But it is easy to see that if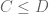 then for any real nonzero t,
then for any real nonzero t,
which implies
Setting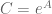 and
and 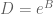 , (5) is then immediate.
, (5) is then immediate.
As regards 3 operators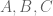 , one notices that in the Ising model and other integrable models,
, one notices that in the Ising model and other integrable models, . This implies by commutation that all
. This implies by commutation that all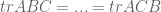 are equal. I believe that this goes to the
are equal. I believe that this goes to the
one always has at hand an extra relation of the type
six of the permutations
heart of the success of the analysis of the Ising model etc., but I have not thought about this
for a while.
Best,
Percy
5 August, 2010 at 12:06 am
Christian Dr. Jaekel
Dear Prof. Tao,
I would like to point out a reference, that you might find helpful:
“Golden-Thompson and Peierls-Bogolubov inequalities for a general von Neumann algebra” by Huzihiro Araki, Comm. Math. Phys. Volume 34, Number 3 (1973), 167-178.”
Best regards,
Christian
16 October, 2010 at 8:58 am
Igor Rivin
For a very simple proof of the G/T inequality you might want to check out my recent arxiv.org preprint
http://arxiv.org/abs/1010.2193
part of the point of which is to give yet another plug for Chandler Davis’ convexity theorem.
16 October, 2010 at 9:22 am
Michael Nielsen
This is very beautiful, and seems like the “right” way of thinking about the result. It’s definitely a great plug for Davis’s convexity theorem, which makes G/T trivial.
3 June, 2019 at 12:54 pm
Anonymous
What you are proving is the much weaker inequality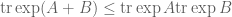 .
.
23 February, 2011 at 6:54 am
Topics in random matrix theory « What’s new
[…] primarily on my graduate course in the topic, though it also contains material from some additional posts related to random matrices on the blog. It is available online here. As usual, comments and […]
27 February, 2013 at 1:42 pm
Chao Gao
Dear Prof. Tao:
I have a question about Frobenius norm. Let || . || be the Frobenius norm. Suppose both the largest eigenvalues of A and B are universally upper bounded. Then is it true that ||A-B|| can be upper and lower bounded by a constant (only depends on the largest eigenvalues of A and B) times ||exp(A)-exp(B)||?
Best,
Chao
10 July, 2014 at 2:19 pm
Effros
Frank Hansen has proved a multivariable version of the Golden-Thompson inequality see the Arxiv.
10 August, 2015 at 4:14 am
On the Chernoff bound | Triforce Studio
[…] EDIT: I found out the simple answer to this question in a nice blogpost by Terry Tao: https://terrytao.wordpress.com/2010/07/15/the-golden-thompson-inequality/ […]
5 October, 2018 at 5:44 am
Rate changes increase substitutions | Bits of DNA
[…] inequality was discovered independently by Sidney Golden and Colin Thompson in 1965. A proof is explained in an expository blog post by Terence Tao who heard of the Golden-Thompson inequality only eight years ago, which makes me feel a […]
17 September, 2021 at 4:36 pm
Adam
Hi, i have a question regarding special version of Chernoff inequality you use at the end of this note. It seems to me that \sigma is missing i.e. it should be P(X1+….XN\geq \lamba \sigma)\leq …. The same in the operator version. Can you check this?
[Corrected, thanks – T.]
10 November, 2021 at 4:12 am
Online Optimization Post 7: Matrix Multiplicative Weights Update | in theory
[…] to generalize to this matrix setting everything we have proved about multiplicative weights. See this post by Terry Tao for a […]