Recall that a (real) topological vector space is a real vector space equipped with a topology
that makes the vector space operations
and
continuous. One often restricts attention to Hausdorff topological vector spaces; in practice, this is not a severe restriction because it turns out that any topological vector space can be made Hausdorff by quotienting out the closure
of the origin
. One can also discuss complex topological vector spaces, and the theory is not significantly different; but for sake of exposition we shall restrict attention here to the real case.
An obvious example of a topological vector space is a finite-dimensional vector space such as with the usual topology. Of course, there are plenty of infinite-dimensional topological vector spaces also, such as infinite-dimensional normed vector spaces (with the strong, weak, or weak-* topologies) or Frechet spaces.
One way to distinguish the finite and infinite dimensional topological vector spaces is via local compactness. Recall that a topological space is locally compact if every point in that space has a compact neighbourhood. From the Heine-Borel theorem, all finite-dimensional vector spaces (with the usual topology) are locally compact. In infinite dimensions, one can trivially make a vector space locally compact by giving it a trivial topology, but once one restricts to the Hausdorff case, it seems impossible to make a space locally compact. For instance, in an infinite-dimensional normed vector space with the strong topology, an iteration of the Riesz lemma shows that the closed unit ball
in that space contains an infinite sequence with no convergent subsequence, which (by the Heine-Borel theorem) implies that
cannot be locally compact. If one gives
the weak-* topology instead, then
is now compact by the Banach-Alaoglu theorem, but is no longer a neighbourhood of the identity in this topology. In fact, we have the following result:
Theorem 1 Every locally compact Hausdorff topological vector space is finite-dimensional.
The first proof of this theorem that I am aware of is by André Weil. There is also a related result:
Theorem 2 Every finite-dimensional Hausdorff topological vector space has the usual topology.
As a corollary, every locally compact Hausdorff topological vector space is in fact isomorphic to with the usual topology for some
. This can be viewed as a very special case of the theorem of Gleason, which is a key component of the solution to Hilbert’s fifth problem, that a locally compact group
with no small subgroups (in the sense that there is a neighbourhood of the identity that contains no non-trivial subgroups) is necessarily isomorphic to a Lie group. Indeed, Theorem 1 is in fact used in the proof of Gleason’s theorem (the rough idea being to first locate a “tangent space” to
at the origin, with the tangent vectors described by “one-parameter subgroups” of
, and show that this space is a locally compact Hausdorff topological space, and hence finite dimensional by Theorem 1).
Theorem 2 may seem devoid of content, but it does contain some subtleties, as it hinges crucially on the joint continuity of the vector space operations and
, and not just on the separate continuity in each coordinate. Consider for instance the one-dimensional vector space
with the co-compact topology (a non-empty set is open iff its complement is compact in the usual topology). In this topology, the space is
(though not Hausdorff), the scalar multiplication map
is jointly continuous as long as the scalar is not zero, and the addition map
is continuous in each coordinate (i.e. translations are continuous), but not jointly continuous; for instance, the set
does not contain a non-trivial Cartesian product of two sets that are open in the co-compact topology. So this is not a counterexample to Theorem 2. Similarly for the cocountable or cofinite topologies on
(the latter topology, incidentally, is the same as the Zariski topology on
).
Another near-counterexample comes from the topology of inherited by pulling back the usual topology on the unit circle
. Admittedly, this pullback topology is not quite Hausdorff, but the addition map
is jointly continuous. On the other hand, the scalar multiplication map
is not continuous at all. A slight variant of this topology comes from pulling back the usual topology on the torus
under the map
for some irrational
; this restores the Hausdorff property, and addition is still jointly continuous, but multiplication remains discontinuous.
As some final examples, consider with the discrete topology; here, the topology is Hausdorff, addition is jointly continuous, and every dilation is continuous, but multiplication is not jointly continuous. If one instead gives
the half-open topology, then again the topology is Hausdorff and addition is jointly continuous, but scalar multiplication is only jointly continuous once one restricts the scalar to be non-negative.
Below the fold, I record the textbook proof of Theorem 2 and Theorem 1. There is nothing particularly original in this presentation, but I wanted to record it here for my own future reference, and perhaps these results will also be of interest to some other readers.
— 1. Proof of Theorem 2 —
Let be a finite-dimensional Hausdorff topological vector space, with topology
. We need to show that every set which is open in the usual topology, is open in
, and conversely.
Let be a basis for the finite-dimensional space
. From the continuity of the vector space operations, we easily verify that the linear map
given by
is continuous. From this, we see that any set which is open in , is also open in the usual topology.
Now we show conversely that every set which is open in the usual topology, is open in . It suffices to show that there is a bounded open neighbourhood of the origin in
, since one can then translate and dilate this open neighbourhood to obtain a (sub-)base for the usual topology. (Here, “bounded” refers to the usual sense of the term, for instance with respect to an arbitrarily selected norm on
(note that on a finite-dimensional space, all norms are equivalent).)
We use to identify
(as a vector space) with
. As
is continuous, every set which is compact in the usual topology, is compact in
. In particular, the unit sphere
(in, say, the Euclidean norm
on
) is compact in
. Using this and the Hausdorff assumption on
, we can find an open neighbourhood
of the origin in
which is disjoint from
.
At present, need not be bounded (note that we are not assuming
to be locally connected a priori). However, we can fix this as follows. Using the joint continuity of the scalar multiplication map, one can find another open neighbourhood
of the origin and an open interval
around
such that the product set
is contained in
. Since
avoids the unit sphere
,
must avoid the region
and is thus bounded, as required.
Corollary 3 In a Hausdorff topological vector space
, every finite-dimensional subspace
is closed.
Proof: It suffices to show that every vector is in the exterior of
. But this follows from Theorem 2 after restricting to the finite-dimensional space spanned by
and
.
— 2. Proof of Theorem 1 —
Let be a locally compact Hausdorff space, thus there exists a compact neighbourhood
of the origin. Then the dilate
is also a neighbourhood of the origin, and so by compactness
can be covered by finitely many translates of
, thus
for some finite set . If we let
be the finite-dimensional vector space generated by
, we conclude that
Iterating this we have
for any . On the other hand, if
is a neighbourhood of the origin, then for every
we see that
for sufficiently large
. By compactness of
(and continuity of the scalar multiplication map at zero), we conclude that
for some sufficiently large
, and thus
for any neighbourhood of the origin; thus
is in the closure of
. By Corollary 3, we conclude that
But is a neighbourhood of the origin, thus for every
we have
for all sufficiently large
, and thus
. Thus
, and the claim follows.

20 comments
Comments feed for this article
24 May, 2011 at 1:18 pm
JuanPi
Hi,
Thanks for the round-up. I am reading . Khatskevich, D.Shoikhet, Differentiable Operators and Nonlinear Equations so this is a nice backup.
Now, I have a more or less green-horn question: If we have D a nonlinear differential operator acting on some Hilbert space of functions. Is there anything we can tell about the set of all solutions q of the problem D(q) = 0? In the linear case we know they are vector space (the nullspace), what can be said in the nonlinear case?
24 May, 2011 at 4:09 pm
Sixth Linkfest
[…] Terence Tao: Stein’s maximal principle, Stein’s spherical maximal theorem, Locally compact topological vector spaces […]
24 May, 2011 at 6:10 pm
MysticTerminator
How is R in the cocompact topology Hausdorff?
[Ah, yes, it isn’t – thanks – T.]
24 May, 2011 at 6:20 pm
Allen Knutson
Theorem 2, as presently stated, is a bit too strong.
[Corrected, thanks – T.]
25 May, 2011 at 4:30 am
Anonymous Rex
Hi, tiny typo: In “Combining the two statements, we see that for every {x \in U”}, we have {sx \in U} for every {x \in (-\epsilon,\epsilon)}”, you use x twice. I assume you mean for s to be the scalar.
[Corrected, thanks – T.]
31 May, 2011 at 1:37 am
Anonymous
Dear Professor Tao,
Grothendieck (MR0372565 (51 #8772)) attributes Theorem 1 to Banach, but
the oldest reference I could find was the 1953 edition of Bourbaki’s TVS
(MR0910295 (88g:46002)), so Weil may have done it first after all.
17 June, 2011 at 2:15 pm
Hilbert’s fifth problem and Gleason metrics « What’s new
[…] space, it must be isomorphic to a finite-dimensional vector space with the usual topology (see this blog post for a […]
4 February, 2012 at 3:39 pm
wildildildlife
In the first sentence below the head ‘1. Proof of Theorem 2 ‘, and in Corollary 3, you write ‘topological space’ which should be ‘topological vector space’.
[Corrected, thanks – T.]
7 May, 2012 at 11:19 am
Richard Hevener
Thanks for a very nice treatment of these results.
I believe the last part of your proof of Thm. 2 can be simplified quite a bit: Given your U, by the continuity of scalar mult., we can find a nbhd. U’ of the origin and a nbhd. N = (-e,e) of 0 such that if x is in U’ and s is in N, then sx is in U. As at the end of your argument, since U avoids the unit sphere, U’ must be contained in the 1/e ball.
[Simplification incorporated, thanks – T.]
7 May, 2012 at 4:20 pm
Richard Hevener
Inside the brackets, you should say (-e,e) instead of (1-e,1+e).
[Corrected, thanks – T.]
7 May, 2012 at 7:52 pm
Richard Hevener
One more typo: again inside the braces, it should be (-e,e) instead of (e,e).
[Gah! Corrected -T.]
7 September, 2013 at 8:27 am
Number of group topologies on the real line | Mathematical Notes
[…] locally compact topological vector space is finite-dimensional (the reader might see Tao’s article on his blog or Bourbaki’s book, Topological vector spaces). Therefore, the weak topologies […]
5 April, 2015 at 11:50 am
Kasper Henriksen
I think I’ve found a slightly different argument that doesn’t require introducing an open neighbourhood $U$ of $0$. If $\dim V = 0$, there is obviously nothing to prove. Otherwise we can write $V$ as the union of its one-dimensional subspaces (“L” is for lines):
\[ \mathcal{L} = \{L \subseteq V : L \leq V,\ \dim L = 1\}. \]
Then
\[ \bigcap_n 2^{-n}K
= \bigcup_{L \in \mathcal{L}} \left(\bigcap_n 2^{-n}K \cap L\right)
= \bigcup_{L \in \mathcal{L}} \{0\}
= \{0\}
\]
by compactness of $K \cap L$ and the fact that $L \cong \mathbb F$.
11 October, 2015 at 7:59 am
Anonymous
Would you elaborate how the Heine-Borel theorem (which says that in a metric space a subset is compact if and only if it is complete and totally bounded) is used here?
11 October, 2015 at 1:49 pm
Terence Tao
The formulation of the Heine-Borel theorem I am using here is that for a metric space X, the properties of (a) being topologically compact (every open cover has a finite subcover), (b) sequentially compact (every sequence has a convergent subsequence), and (c) being complete and totally bounded, are equivalent. For this particular application only the equivalence of (a) and (b) is needed.
11 October, 2015 at 8:16 am
Anonymous
What does the “usual topology” mean in the statement of Theorem 2? Let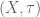 be a hausdorff TVS (over
be a hausdorff TVS (over 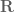 ) of finite dimension
) of finite dimension  . Do you mean that
. Do you mean that  must be the standard topology on
must be the standard topology on 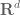 , which means you are identifying
, which means you are identifying  with
with 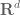 ?
?
11 October, 2015 at 1:51 pm
Terence Tao
Yes. Or more precisely, one selects a linear isomorphism between and
and 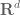 , and then uses this isomorphism to pull back the usual topology on
, and then uses this isomorphism to pull back the usual topology on 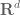 . This is independent of the choice of isomorphism, because all linear maps from
. This is independent of the choice of isomorphism, because all linear maps from 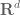 to itself are automatically continuous in the standard topology.
to itself are automatically continuous in the standard topology.
9 June, 2019 at 3:40 am
Adam
In the proof of Theorem 1, why does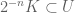 for some large enough
for some large enough  ? From compactness there exists a finite set
? From compactness there exists a finite set  such that,
such that, 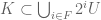 . It seems for me that the (non-obvious, and probably not true) fact that for
. It seems for me that the (non-obvious, and probably not true) fact that for  ,
,  , was used.
, was used.
9 June, 2019 at 3:56 am
Adam
I’ve looked up more. I found that we can assume without loss of generality that U is a balanced set, which fixes every problem I had earlier.
13 February, 2023 at 7:51 am
Jochen Wengenroth
Theorem 2 is stated and proved in A. Tychonoff, Ein Fixpunktsatz, Math. Ann. 111, 767–776 (1935).