In the tradition of “Polymath projects“, the problem posed in the previous two blog posts has now been solved, thanks to the cumulative effect of many small contributions by many participants (including, but not limited to, Sean Eberhard, Tobias Fritz, Siddharta Gadgil, Tobias Hartnick, Chris Jerdonek, Apoorva Khare, Antonio Machiavelo, Pace Nielsen, Andy Putman, Will Sawin, Alexander Shamov, Lior Silberman, and David Speyer). In this post I’ll write down a streamlined resolution, eliding a number of important but ultimately removable partial steps and insights made by the above contributors en route to the solution.
Theorem 1 Let
be a group. Suppose one has a “seminorm” function
which obeys the triangle inequality
for all
, with equality whenever
. Then the seminorm factors through the abelianisation map
.
Proof: By the triangle inequality, it suffices to show that for all
, where
is the commutator.
We first establish some basic facts. Firstly, by hypothesis we have , and hence
whenever
is a power of two. On the other hand, by the triangle inequality we have
for all positive
, and hence by the triangle inequality again we also have the matching lower bound, thus
for all . The claim is also true for
(apply the preceding bound with
and
). By replacing
with
if necessary we may now also assume without loss of generality that
, thus
Next, for any , and any natural number
, we have
so on taking limits as we have
. Replacing
by
gives the matching lower bound, thus we have the conjugation invariance
Next, we observe that if are such that
is conjugate to both
and
, then one has the inequality
Indeed, if we write for some
, then for any natural number
one has
where the and
terms each appear
times. From (2) we see that conjugation by
does not affect the norm. Using this and the triangle inequality several times, we conclude that
and the claim (3) follows by sending .
The following special case of (3) will be of particular interest. Let , and for any integers
, define the quantity
Observe that is conjugate to both
and to
, hence by (3) one has
which by (2) leads to the recursive inequality
We can write this in probabilistic notation as
where is a random vector that takes the values
and
with probability
each. Iterating this, we conclude in particular that for any large natural number
, one has
where and
are iid copies of
. We can write
where
are iid signs. By the triangle inequality, we thus have
noting that is an even integer. On the other hand,
has mean zero and variance
, hence by Cauchy-Schwarz
But by (1), the left-hand side is equal to . Dividing by
and then sending
, we obtain the claim.
The above theorem reduces such seminorms to abelian groups. It is easy to see from (1) that any torsion element of such groups has zero seminorm, so we can in fact restrict to torsion-free groups, which we now write using additive notation , thus for instance
for
. We think of
as a
-module. One can then extend the seminorm to the associated
-vector space
by the formula
, and then to the associated
-vector space
by continuity, at which point it becomes a genuine seminorm (provided we have ensured the symmetry condition
). Conversely, any seminorm on
induces a seminorm on
. (These arguments also appear in this paper of Khare and Rajaratnam.)

141 comments
Comments feed for this article
21 December, 2017 at 4:28 pm
Terence Tao
Thanks to everyone who participated! The project ended up being a de facto Polymath project, and played out much as other successful such projects have – with a large number of small observations that, despite some corrections and backtracking, did cause the project to ultimately converge towards a final solution, and in a manner much faster than if just a handful of us were working on the problem.
The result looks interesting enough (and non-trivial enough) to publish, possibly under the usual “D.H.J. Polymath” pseudonym. (Our tradition in that case is for participants to report their name, affiliation, and (if applicable) grant support) on the corresponding wiki page, rather than being listed in the published paper.); let me know what you all think about this. One should of course look to see if there are any applications or generalisations for the result… maybe Apoorva can tell us a bit more about the motivation for the problem?
21 December, 2017 at 6:30 pm
Pace Nielsen
I just got back from a family gathering to see the problem was finished up.
Great job everyone, and thanks Terry and Apoorva for giving us this problem to think about!
22 December, 2017 at 3:33 am
Tobias Fritz
It would be great to have it published, and I’d be happy to help with the writing to the best of my abilities as a member of D.H.J. Polymath.
(Technically I should be working on things that could please hiring committees. But then again I don’t want to adapt my work to that.)
22 December, 2017 at 10:08 am
Lior Silberman
I also support publishing, naturally under the psedonym. Tobias: I’m not sure about the exact etiquette, and Terry has more experience, but I’m fairly certain you may include this paper in your list of publications.
22 December, 2017 at 10:24 am
Terence Tao
I include the Polymath papers I was involved in my own “unofficial” list of publications, but my institution doesn’t formally accept them as publications under my name. However, they can still be entered in as “other work”. Also I think it is completely appropriate to list yourself as a contributor to the project in talks, research statements, citations in other papers, etc..
I’ll start a skeleton draft of a paper on a Dropbox folder later today and share it with you all soon.
Three unrelated retrospective comments about this project. Firstly, as with Polymath8 (bounded gaps between primes), it seemed to be quite helpful to have a quantitative way of measuring progress. In Polymath8, it was the bound on gaps between primes; here, it was the bound on![\|[a,b]\|](https://s0.wp.com/latex.php?latex=%5C%7C%5Ba%2Cb%5D%5C%7C&bg=ffffff&fg=545454&s=0&c=20201002) . Because of this scorekeeping mechanism, it became easier to identify the most promising techniques and focus attention on them.
. Because of this scorekeeping mechanism, it became easier to identify the most promising techniques and focus attention on them.
Secondly, again as with some previous Polymath projects, computer assistance was quite important, even if the final proof is not visibly computer-assisted in any way. In particular, the crucial “inward repetition” technique (now formalised in the proof of the inequality (3) above) was discovered by deconstructing some inequalities that were computer generated. We’re still some way off from the dream of computers routinely generating large chunks of proofs and/or conjectures for us, but nevertheless they are playing an increasingly essential role in mathematics.
Finally, I just wanted to observe that the proof techniques here are implicitly using (a variant of) the “tensor power trick“, which is one of my favourite techniques in analysis, particularly with regards to how it can “magically” eliminate lower order error terms from one’s bounds by taking the tensor power limit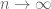 .
.
For posterity, it might be nice for other participants to record any impressions they had on the project (particularly with regards to any suggestions on how to improve future projects of this type).
22 December, 2017 at 11:39 am
Apoorva Khare
These are three very informative observations, Terry!
Speaking of the Wiki page for this Polymath, can it be found on the main Polymath page:
http://www.michaelnielsen.org/polymath1/index.php?title=Main_Page
or should I be looking somewhere else?
22 December, 2017 at 12:24 pm
Lior Silberman
Yes — on the main Polymath wiki page look for the last item in the section “Polymath-like projects”
22 December, 2017 at 12:47 pm
Lior Silberman
Terry: would you consider trying a source control system (e.g Subversion) instead of dropbox? Our department has a server so I can host the project.
22 December, 2017 at 2:18 pm
Terence Tao
I think this particular project is simple enough (the paper is likely to just be six or seven pages) that we won’t need more advanced version control, but this is certainly something to consider in the future. (Usually for polymath projects we have a separate planning thread running concurrently with the research in which these things can be worked out, but this particular project started and ended too quickly to set all this up.)
From my experience, though, while almost all participants are willing to use Dropbox, there are some who are not as keen on using version control such as Subversion (and if one switches to even more sophisticated control systems such as git, then the enthusiasm can dip even lower). Dropbox seems “good enough” for small and medium sized writing projects, particularly if one breaks up files into pieces to help avoid edit conflicts. I certainly agree though that more advanced version control would be desirable if one had a more complicated project (e.g. a monograph).
Of course, if the other editors of the paper prefer Subversion (or some other platform) over Dropbox, it would be relatively easy to transfer over at this stage.
EDIT: one thing about Dropbox: it helps if people announce on this blog if they are going to perform substantial edits on a section of the paper, and then to also announce when they are done editing. However, quick minor edits can usually be done without any such announcement (provided that nobody else is claiming a “lock” on the relevant section). This is of course the price one pays for not having more sophisticated version control in place…
24 December, 2017 at 8:21 am
Siddhartha Gadgil
Firstly, this experience has been truly enjoyable – thanks to everyone for this.
An observation: one useful feature here was an “adversarial approach” – trying to construct semi-norms positive on commutators, while trying to rule these out. While this is normal in mathematics, it may be easier in polymath projects as it needs fewer mental switches, and also we have a range of attacks based on the ways of thinking of the participants.
21 December, 2017 at 5:12 pm
Anonymous
This solution seems to be from “the Book” !
21 December, 2017 at 5:49 pm
Siddhartha Gadgil
Looks like this elegant proof gives a quantitative refinement (applicable in particular to quasi-morphisms) where we replace the triangle inequality by
where we have
If this holds, it is a curious rigidity phenomenon.
21 December, 2017 at 10:01 pm
Siddhartha Gadgil
That was too hopeful, but it looks like the norm of the commutator is bounded by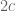 , which for actual semi-norms gives the result.
, which for actual semi-norms gives the result.
21 December, 2017 at 8:29 pm
Lior Silberman
Erratum: in the probabilistic inequality no need to take norm of , while in the next sentence it’s
, while in the next sentence it’s  that is the Euclidean norm in the plane.
that is the Euclidean norm in the plane.
[Corrected, thanks -T.]
Finally, in the probabilistic context this usage of Cauchy–Schwarz is often called Chebycheff’s inequality, but it’s a matter of taste.
21 December, 2017 at 8:37 pm
Lior Silberman
Sorry — I’m wrong about the name of the inequality.
23 December, 2017 at 4:58 am
Tobias Fritz
I’m still a bit confused about the Cauchy-Schwarz inequality there. How exactly does that work? It’s clear by Jensen’s inequality and the concavity of the square root,
but I don’t see how to do it with Cauchy-Schwarz. Can anyone clear this up?
23 December, 2017 at 6:16 am
Anonymous
It is simply applied to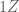
22 December, 2017 at 12:00 am
Avi Levy
Just before the last display in the proof of Theorem 1, you refer to the random variable (call it
(call it  ) as having variance
) as having variance  . But
. But  is two-dimensional, so I’m not sure what this means exactly – and in fact, its covariance matrix is not even diagonal. However, by a simple calculation
is two-dimensional, so I’m not sure what this means exactly – and in fact, its covariance matrix is not even diagonal. However, by a simple calculation  , yielding the (slightly weaker but still sufficient) estimate
, yielding the (slightly weaker but still sufficient) estimate ![f(0,n)\leq \sqrt{\frac{5n}{4}}(\|x\|+\|[x,y]\|)](https://s0.wp.com/latex.php?latex=f%280%2Cn%29%5Cleq+%5Csqrt%7B%5Cfrac%7B5n%7D%7B4%7D%7D%28%5C%7Cx%5C%7C%2B%5C%7C%5Bx%2Cy%5D%5C%7C%29&bg=ffffff&fg=545454&s=0&c=20201002) . Perhaps this was what was intended all along?
. Perhaps this was what was intended all along?
[Corrected, thanks – T.]
22 December, 2017 at 1:30 am
Anonymous
It also seems clearer to call “random vector” (instead of “random variable”)
“random vector” (instead of “random variable”)
[Corrected, thanks – T.]
22 December, 2017 at 3:18 am
Anonymous
Since the random vector is degenerate (its covariance matrix has rank 1), it seems clearer to represent it by

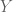 is a random variable, taking the values
is a random variable, taking the values 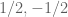 with probability
with probability 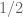 each. Hence
each. Hence
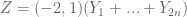 which implies
which implies
![f(Z) \leq (2||x|| + ||[x,y]||) |y_1 + ... + y_{2 n}|](https://s0.wp.com/latex.php?latex=f%28Z%29+%5Cleq+%282%7C%7Cx%7C%7C+%2B+%7C%7C%5Bx%2Cy%5D%7C%7C%29+%7Cy_1+%2B+...+%2B+y_%7B2+n%7D%7C&bg=ffffff&fg=545454&s=0&c=20201002)
 .
.
where
whose expectation is
[Suggestion implemented, thanks – T.]
22 December, 2017 at 3:45 am
Tobias Fritz
To get the optimal bound that follows from that method, we could also use the fact that is supported on a one-dimensional subspace, apply the central limit theorem there, and use the known expectation value of the half-normal distribution. I don’t have time to do this now, but I could do it later.
is supported on a one-dimensional subspace, apply the central limit theorem there, and use the known expectation value of the half-normal distribution. I don’t have time to do this now, but I could do it later.
22 December, 2017 at 7:41 am
Tobias Fritz
But of course, optimizing the constant is completely pointless, since what we’re showing is that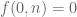 anyway.
anyway.
22 December, 2017 at 6:47 am
Apoorva Khare
First, I am delighted that the problem was solved so fast! I will be happy to make this into a paper, and both options are fine by me: DHJ Polymath with actual names on the Wiki, or all author names in the paper (in the spirit of AIM workshops, say). I am glad to go along with Terry’s preference for a DHJ Polymath paper.
As Terry wrote above, we should look for (and I think are discussing already on the blog) possible applications, related results, and generalizations. Together with Siddhartha Gadgil (who is also my colleague at IISc), I have collected these “related questions” in my next comment below, and mostly they are solved by now. We may want to include some/all of them in the paper.
But first, I mention a few remarks re: my motivations. If our result has other applications, say in geometric group theory, I would be very happy to hear about them as well.
(1) My motivation comes from a collection of joint works with Bala Rajaratnam, in which we explore stochastic inequalities. For example, in a paper in Annals of Probability 2017, also available on arXiv, we show that the Hoffmann-Jorgensen inequality, which can be stated using only a semigroup operation and a metric, can also be proved using just these tools. (In particular, it holds not only for Banach spaces but also for e.g. non-abelian compact Lie groups.)
In our preprint Terry cited above, we tackle similarly the Khinchin-Kahane inequality, this time over any abelian metric group. When the group is also “normed” (i.e., the metric has linear growth), we obtain the same sharp constants as in the Banach space case. As it turns out, this is because every normed metric group (or semigroup, monoid…) that is abelian, can be isometrically embedded in a Banach space. (There are several consequences of this, including defining expectations of random variables taking values in normed abelian semigroups; categorical constructions of these covers, etc.) The proof of this set of embeddings is precisely what Terry has sketched above.
Now one can ask: what happens if “abelian” is replaced by “non-abelian”, as in the first paragraph? In this case the precursor to any embedding question is existence… and this was not known in general, until this Polymath. (A special case was known: work of Milnor showed that connected non-abelian Lie groups with linear norms don’t exist.)
(2) These embedding questions for abelian (semi)groups into Banach spaces are also connected to nearly additive mappings and separation theorems in functional analysis. See work of Cabello Sanchez and Castillo, and Gajda and Kominek, which identify when (linearly) normed abelian groups embed isometrically into Banach spaces.
22 December, 2017 at 7:04 am
Apoorva Khare
Now for the “related problems” involving linear seminorms, which I have compiled together with Siddhartha Gadgil. It turns out that a majority of these are fairly simple observations to make, so we just mention a few remarks.
(1) The first involves the “main question”. There are two variants:
(a) Does there exist a non-abelian group G with a linear norm (i.e., that is positive outside the identity)?
(b) Does every linear seminorm of a group G factor through its (torsion-free) abelianization?
Note that (a) and (b) are equivalent, as the norm-zero elements form a normal subgroup of G. However, (a) and (b) are not equivalent when restricted to a specific group G. The main theorem above resolves these questions for every group G.
—-
(2) The original theorem was a “rigidity” result (see (1)(b)). However, if we weaken any of the conditions, then either examples exist or the condition turns out to be equivalent to the original problem:
(a) If we replace “groups” by “monoids”, then examples indeed exist. Consider [via Robert Young] the free monoid on any alphabet, with the (edit) distance between strings v,w being the least number of single generator insertions and deletions to get from v to w. The triangle inequality and positivity are standard; linearity is trivial; and the bi-invariance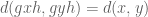 follows by considering
follows by considering  {generator, identity}.
{generator, identity}.
(b) If we replace “linear growth” by “almost linear growth”, then Tobias Hartnick’s two comments show existence.
(c) The other case of “almost linear” was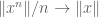 for all
for all  — but this is clearly linear, by Sean Eberhard.
— but this is clearly linear, by Sean Eberhard.
(d) David Speyer asked a different question, about which Sean Eberhard has some thoughts. Can this be answered?
(e) Although there is no linear norm on a non-abeliam group, it can indeed be defined on finite diameter balls in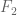 . See the discussion/comments following this analysis by Terry.
. See the discussion/comments following this analysis by Terry.
(f) The final case is when “seminorm” is replaced by “quasi-seminorm with additive constant c” — as asked by Siddhartha Gadhil. He mentioned to me that he will post more details on this variant, and has done so just a few minutes ago (following this post).
22 December, 2017 at 1:26 pm
SH
Your motivation sounds like the Ribe program for metric groups.
22 December, 2017 at 5:28 pm
Apoorva Khare
Thanks!
22 December, 2017 at 6:55 am
Siddhartha Gadgil
As I mentioned before, a natural extension is to consider linear quasi-semi-norms, i.e., with
for a fixed constant . Examples that do not vanish on the commutator are obtained by taking the norm of a homgeneous quasi-morphism.
. Examples that do not vanish on the commutator are obtained by taking the norm of a homgeneous quasi-morphism.
It is easy to see that in this case, the above argument shows that for all elements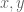 in the group, the commutator
in the group, the commutator ![[x, y]](https://s0.wp.com/latex.php?latex=%5Bx%2C+y%5D&bg=ffffff&fg=545454&s=0&c=20201002) has norm at most
has norm at most 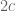 . Essentially each application of the triangle inequality gives an extra
. Essentially each application of the triangle inequality gives an extra  term, so taking the sum of the
term, so taking the sum of the 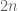 random variables gives an extra
random variables gives an extra 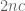 term in the bound of
term in the bound of 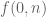 . Note that this is uniform over all commutators (even commutators of very large elements).
. Note that this is uniform over all commutators (even commutators of very large elements).
The above examples show this refinement is essentially sharp.
22 December, 2017 at 7:39 am
Lior Silberman
I think you might be a little off: it seems to me that inequality (3) should also have a , so you’d lose
, so you’d lose 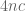 overall.
overall.
22 December, 2017 at 9:12 am
Anonymous
Wow!This is really gift for Christmas holiday.Terry,thank you very much.
22 December, 2017 at 1:46 pm
Terence Tao
I’ve started a dropbox folder for the paper at
https://www.dropbox.com/sh/wg4y7ptahwq3xo1/AABreDLrXH3hniz1jiFTtvska?dl=0
with the current draft being available as linear.pdf. I have the proof of the main argument (allowing for a loss of in the triangle inequality – I ended up with a net loss of
in the triangle inequality – I ended up with a net loss of 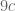 , but perhaps this could be improved). One needs to fill in an introduction and a remarks section – perhaps Apoorva would be willing to start with that?
, but perhaps this could be improved). One needs to fill in an introduction and a remarks section – perhaps Apoorva would be willing to start with that?
If anyone else wishes to help with the editing, send me an email (at tao@math.ucla.edu) and I will be able to give edit privileges to the dropbox folder. (Of course one would need to have dropbox installed on one’s own computer for this.)
Also, if all contributors could add their name, affiliation, and any grant information to http://michaelnielsen.org/polymath1/index.php?title=Linear_norm_grant_acknowledgments , that would be great.
22 December, 2017 at 1:54 pm
Apoorva Khare
I’m glad to work on the introduction today morning my time. For now, let me add the contents of my second comment on the latest blogpost, to the remarks file, before I retire. And I’ll add a couple of small edits in blue, to the linear.tex file. As always, people can modify in the next version. I should be done in at most an hour’s time.
22 December, 2017 at 3:22 pm
Apoorva Khare
Sorry, it took a little more time. I am now done, the latest files are on Dropbox, and my edits are in blue. Please edit the files as you see fit — especially the various results in “related settings”, which are added to the “remarks.tex” file.
I will add to the Introduction file tomorrow, and hopefully the Abstract goes last of all.
By the way, I don’t know how we want to work this out – should the next person write a different version number for each file they edit? E.g. remarks-v2.tex, etc.
22 December, 2017 at 3:26 pm
Apoorva Khare
PS> As you can see in Sections 2,3 –> I refer to an as-yet-unstated theorem from the Introduction. I’m currently inclined for us to state the theorem proved on the blog in the Introduction, and then say that we’ll show the more general quantitative estimate for “quasinorms of commutators” in the next section, before exploring variants in Section 3.
22 December, 2017 at 3:52 pm
Terence Tao
Thanks for this! Dropbox has the ability to view and restore older versions of files, and I doubt there will be many controversial edits to the paper, so I think it won’t be necessary to manually insert version numbers for now.
I also agree with stating a c=0 version of the main theorem in the introduction and say at some point that we actually prove a more robust version.
23 December, 2017 at 3:57 am
Tobias Fritz
Thank you for sharing the draft! I don’t have Dropbox installed, and in previous collaborations I have always downloaded and uploaded manually. If this turns out to be a problem, then I’ll be happy to install it.
As far as I know, the standard term for a “norm” on a group (satisfying the triangle inequality, symmetry and non-degeneracy is length function, so I’ve switched to this in the title, abstract, and introduction. The downside is that this standard term misleadingly suggests a relation to word length. Let me know what you think; I’ll be happy to revert it if you all don’t like it.
and non-degeneracy is length function, so I’ve switched to this in the title, abstract, and introduction. The downside is that this standard term misleadingly suggests a relation to word length. Let me know what you think; I’ll be happy to revert it if you all don’t like it.
I’m now going through the main text. One thing that I find curious is that we’re not making the symmetry assumption in Theorem 2.1. As I go along, I will carefully check whether we really don’t need it.
in Theorem 2.1. As I go along, I will carefully check whether we really don’t need it.
By the way, is this the right place to discuss the draft or should we do this somewhere else?
23 December, 2017 at 4:57 am
Siddhartha Gadgil
I am tempted to “initialize git” in the Dropbox folder – those who don’t use git can simply ignore this as if no change was made, but it does help workflow for those of us who do. Is this fine?
23 December, 2017 at 5:02 am
Apoorva Khare
I am fine with initializing git.
23 December, 2017 at 5:14 am
Siddhartha Gadgil
I have initialized git, with the understanding that it is used in a way that it can be completely ignored by those who do not want to use it. I
23 December, 2017 at 7:48 am
Terence Tao
Ah. that’s a nice compromise! Sure, go ahead and do this.
23 December, 2017 at 7:58 am
Terence Tao
OK, it should be fine if you upload (or email to one of us) your edits manually, or Siddharta can give you git access if you use that. This post is certainly the best place to discuss the writing of the paper, since the research aspect seems to be largely wrapped up at this point.
Length functions: sure, if this is the standard term in the literature then we can switch. What I’ll do now is make a macro, say \norm{x}, for \ell(x), so if we ever decide later to change notation again then we just need to change that one macro and not the whole text.
23 December, 2017 at 8:39 am
Terence Tao
I’ve now switched the notation over to length functions, and am working on stating a main theorem.
23 December, 2017 at 9:57 am
Terence Tao
I am now done editing for now. I changed “linear growth” to “homogeneous”, because of the fact that there are certainly non-abelian length functions (e.g. word metric on free group) in which the length of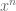 grows linearly with
grows linearly with  , but is not homogeneous.
, but is not homogeneous.
22 December, 2017 at 7:57 pm
Siddhartha Gadgil
To complete the perturbed case , i.e., for quasi-seminorms, (following an earlier idea of Tobia Fritz) it is an immediate consequence of the bound![\|[g, h]\| \leq 9c](https://s0.wp.com/latex.php?latex=%5C%7C%5Bg%2C+h%5D%5C%7C+%5Cleq+9c&bg=ffffff&fg=545454&s=0&c=20201002) for all
for all 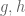 that if
that if 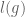 denotes the commutator length of
denotes the commutator length of 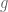 , i.e., the length of the shortest expression of
, i.e., the length of the shortest expression of 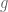 as a product of commutators, then
as a product of commutators, then 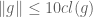 .
.
Conversely, let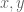 be the generators and
be the generators and 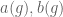 the corresponding homomorphisms onto
the corresponding homomorphisms onto 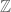 . We define
. We define
which we see is a quasi-norm. We homogenize this and define
Finally, for a real number , we define
, we define
What we seem to get is that every quasi-seminorm is essentially bounded by this. Topologically this is nice as it is essentially a Gromov norm (genus of a bounding surface) after making a chain into a cycle using a specific section.
23 December, 2017 at 9:02 am
Apoorva Khare
Once Terry is done with his edits (which he is carrying out), and since Tobias Fritz and Siddhartha Gadgil have earlier added their edits, I would like to go next (as it is nighttime here and I will soon stop). I’ll quickly work on the “non-Intro” files first, and put them up and report here; and then work at length on the Intro file.
23 December, 2017 at 1:08 pm
Apoorva Khare
The main theorem looks very nice! Also, I am done with my edits for now (as it is late here), and have uploaded the files back to Dropbox. I couldn’t get to adding to the Introduction and then to the Abstract, but should be able to do so on Sunday.
I also found a possibly incomplete argument on page 7. Finally, I was also thinking of alluding to (Naor’s survey of) the Ribe program in the introduction; if anyone can say more about this, please consider revising the file after my edits tomorrow.
23 December, 2017 at 1:58 pm
Terence Tao
I clarified the argument on page 7: the point is that the abstract construction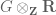 of a vector space containing
of a vector space containing  may not necessarily be compatible with any pre-existing embedding of
may not necessarily be compatible with any pre-existing embedding of  into a vector space. In particular, if
into a vector space. In particular, if 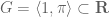 , then
, then 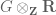 is not embedded into
is not embedded into 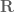 , in fact it is a two-dimensional space. In particular, in
, in fact it is a two-dimensional space. In particular, in 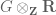 , the two generators
, the two generators  of
of  are linearly independent over
are linearly independent over 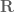 , even though they were not linearly independent in the pre-existing embedding.
, even though they were not linearly independent in the pre-existing embedding.
23 December, 2017 at 2:14 pm
Apoorva Khare
Great! After uploading the files, it occurred to me to simply use the triangle inequality and reduce the question to the real-span of a single element, for which it follows from homogeneity in a one-dimensional Banach space. Anyway – your footnote-2 captures and clarifies the key point very well.
23 December, 2017 at 4:26 pm
Siddhartha Gadgil
I made a picture of the curves x, y, z and w in the iterated cancellation lemma, which is at https://github.com/siddhartha-gadgil/Superficial/blob/master/xywz.jpg and also in the Dropbox folder.
The curves are on a 2-holed Klein bottle, obtained by identifying the two boundary components labelled x.
It is not clear to me if this picture illuminates anything but (like the computer calculations) smarter people may be able to get something from it.
24 December, 2017 at 8:08 am
Siddhartha Gadgil
I have written the quasi version, and am stopping for now. I am using git locally, so I am editing in parallel but will ensure that I do not mess up with parallel editing.
24 December, 2017 at 8:43 am
Apoorva Khare
Following the edits of Tobias and Siddhartha, I made a few minor edits and re-uploaded the various TeX files. I will work on the introduction tomorrow morning my time (i.e. today evening US time).
24 December, 2017 at 5:25 pm
Apoorva Khare
I started editing the files about an hour back, and finished all but the Introduction, on which I will work now. That said, all five files are re-uploaded to Dropbox. Apart from editing small typos (like yesterday), I added a global macro \free to use in place of free groups – thus far we only use \free{2}.
Here is a further question: in Corollary 1.2, we show that if a group has a homogeneous length function, then it is abelian and torsion-free, and by the main theorem, it embeds isometrically inside a Banach space. The converse is immediate. Now I’m wondering: which (abelian, torsion-free) groups admit homogeneous length functions? If G is finitely generated then it is free, hence we are good; and if G has Prufer rank 1 then I think it embeds inside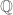 . What happens more generally? E.g. there’s an old paper by Baer in [Duke 1937], but I am not an expert in this.
. What happens more generally? E.g. there’s an old paper by Baer in [Duke 1937], but I am not an expert in this.
24 December, 2017 at 5:40 pm
Terence Tao
I think every abelian torsion-free group admits a homogeneous length function; the arguments in the paper already embed such a group in a real vector space, and an easy application of Zorn’s lemma shows that every vector space admits at least one norm.
24 December, 2017 at 5:45 pm
Apoorva Khare
Aha, a very satisfying conclusion! Let me add that as well to the Introduction, as I continue editing. (I assume we will soon run out of additions, at which point someone – Terry perhaps? – could go through the paper, and reorganize, polish, and make the writing style “homogeneous” (sorry for the choice of word).)
25 December, 2017 at 5:51 am
Apoorva Khare
I am now done adding to the Introduction and also some minor edits to the files. This ends my additions to all files (for now). Please feel free to reword/condense/polish/remove etc.
25 December, 2017 at 12:30 am
Avi Levy
Just wanted to point out that it seems Proposition 2.1 (the “key proposition”) in the dropbox file can be recast as an inequality for arbitrary non-negative functions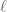 on a group
on a group  :
:
![\sup_{x,y\in G}\ell([x,y])\leq 9\max\{\inf_{x,y\in G}\ell(xy)-\ell(x)-\ell(y),\inf_{x\in G}2\ell(x)-\ell(x^2),0\}](https://s0.wp.com/latex.php?latex=%5Csup_%7Bx%2Cy%5Cin+G%7D%5Cell%28%5Bx%2Cy%5D%29%5Cleq+9%5Cmax%5C%7B%5Cinf_%7Bx%2Cy%5Cin+G%7D%5Cell%28xy%29-%5Cell%28x%29-%5Cell%28y%29%2C%5Cinf_%7Bx%5Cin+G%7D2%5Cell%28x%29-%5Cell%28x%5E2%29%2C0%5C%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Also, a careful inspection of the proof could yield local versions of this inequality – one could start by bounding
. Also, a careful inspection of the proof could yield local versions of this inequality – one could start by bounding ![\ell([x,y])](https://s0.wp.com/latex.php?latex=%5Cell%28%5Bx%2Cy%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) for specific
for specific  by the corresponding quanties where the infima are taken over the subgroup generated by
by the corresponding quanties where the infima are taken over the subgroup generated by  rather than all of
rather than all of  , for instance.
, for instance.
25 December, 2017 at 6:26 am
Apoorva Khare
Very nice! Also, shouldn’t the local version follow then as the special case ?
?
25 December, 2017 at 1:12 pm
dcohen
Does the result extend to groupoids? Of course the doubling condition doesn’t make sense, but one could require instead, in addition to conjugacy invariance, that for all , there exists
, there exists 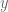 such that
such that  . Does it work for groups already? (maybe trivially not)
. Does it work for groups already? (maybe trivially not)
25 December, 2017 at 2:17 pm
Terence Tao
Well, if then there always exists a
then there always exists a 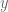 , just take
, just take 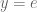 . Or, if one insists on
. Or, if one insists on 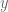 the same length as
the same length as  , one can take the usual word length on the free group on two generators, then for every
, one can take the usual word length on the free group on two generators, then for every  there will be a
there will be a 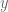 of the same length such that
of the same length such that 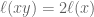 .
.
In Section 4.1 of the draft there is an observation that the edit distance on free monoids is a non-trivial homogeneous length function, so the ability to take inverses is crucial in the main theorem.
25 December, 2017 at 2:39 pm
dcohen
Ah right,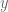 should not be the identity indeed. But the word metric isn’t bi invariant or am I confused?
should not be the identity indeed. But the word metric isn’t bi invariant or am I confused?
25 December, 2017 at 4:29 pm
dcohen
To clarify the (maybe stupid) intuition for the above relaxed doubling condition, I was thinking of a generalization of the following form:
Consider a length space with a transitive isometric action such that each point has trivial stabilizer. Assume also that any minimal geodesic can be extended infinitely while remaining minimal. Is the group necessarily commutative?
I think this is more or less equivalent to the relaxed condition above.
Perhaps this generalization is obviously false or useless, but I was feeling that since the original question had a geometric flavor, maybe it made sense to formulate a more geometric version.
25 December, 2017 at 4:42 pm
dcohen
by minimal geodesic I mean a geodesic that realizes the distance. Maybe minimizing geodesic is better
25 December, 2017 at 5:13 pm
dcohen
ok this is stupid, conditions are too weak, a tree would work.
25 December, 2017 at 5:21 pm
Andrey
Do you think a version of this theorem could hold for stably unbounded quasi-norms on F_2 in the sense of Burago-Ivanov-Polterovich?
https://arxiv.org/abs/0710.1412
25 December, 2017 at 6:55 pm
dcohen
If you send the two generators to two generic symmetric matrices, you get a linear representation of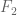 . Now the logarithm of the condition number pulls back to a quasi-norm. Generically, all obtained matrices have at least two eigenvalues, implying that the quasi-norm is stably unbounded (unless I’m mistaken).
. Now the logarithm of the condition number pulls back to a quasi-norm. Generically, all obtained matrices have at least two eigenvalues, implying that the quasi-norm is stably unbounded (unless I’m mistaken).
25 December, 2017 at 9:30 pm
Pace Nielsen
Just got done with some minor edits. For instance: at the very end of the proof of the splitting lemma, I changed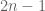 to
to  to account for the two extra
to account for the two extra  ‘s coming from splitting off the
‘s coming from splitting off the 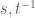 at the beginning and ending of
at the beginning and ending of  . (Someone want to double-check I got that right?)
. (Someone want to double-check I got that right?)
I also made it so the equation numbering and theorem numbering was sequential. I personally like this, to make it easier to find numbered equations, but if anyone is opposed to this change, it can easily be changed back.
I think everything else was minor and non-controversial.
As I was reading through the paper I didn’t understand the paragraph starting “To rectify the situation…” Perhaps someone could clarify this paragraph a bit more.
There is a reference to [5, Theorem B]. There doesn’t appear to be a Theorem B in that paper. Was that supposed to be 8?
In the bounds on Proposition 4.5 (under the new numbering): Shouldn’t the constant c show up on the RHS (in both inequalities)?
Finally, at the end of the paper, it appears that additive and multiplicative notations are being used simultaneously.
[If there is a better place to put these comments than on the blog–say somewhere in the dropbox folder–please feel free to move them there.]
25 December, 2017 at 10:33 pm
Apoorva Khare
@Pace:
Thank you for the edits and finding these polishings! I added the paragraph “To rectify the situation…” in order to mention various attempts that were made to attack the problem, consulting Siddhartha Gadgil to some extent. But of course I am not an expert and my language is subject to much improvement, I’m sure. So please feel free (applies to others as well) to rephrase / do major edits / etc. Ditto for the remainder of Section 1.
Also, I verified your calculation and it seems correct to me.
I’m fine with either mode of equation numbering, so will leave what you have done as is. (I used to prefer this scheme as well.)
I can correct the additive notation at the end of the paper.
Finally, the reference to [5, Theorem B] should be to [7, Theorem B]. I will make these edits (and also a few more I had located as I re-read through the paper), in about 3-4 hours when it is safe to assume it’s late in the US.
26 December, 2017 at 9:50 am
Pace Nielsen
@Apoorva: Thanks for making those changes!
—————-
@All: In Proposition 4.5, shouldn’t the first inequality read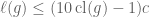 ? [To take into account the extra
? [To take into account the extra  ‘s coming from breaking apart the product of commutators, in order to apply Proposition 2.1.] If so, similar changes would need to be made to the second inequality.
‘s coming from breaking apart the product of commutators, in order to apply Proposition 2.1.] If so, similar changes would need to be made to the second inequality.
26 December, 2017 at 12:42 pm
Terence Tao
Fixing that now. (Also made a number of other minor edits, mostly with regards to harmonising notation.)
I’m trying to verify the claim after Prop 4.5 in which it is asserted that all conjugacy invariant length functions obey![\ell([a^k,b^m]) \leq \min( |k| \ell(a), |m| \ell(b) )](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ba%5Ek%2Cb%5Em%5D%29+%5Cleq+%5Cmin%28+%7Ck%7C+%5Cell%28a%29%2C+%7Cm%7C+%5Cell%28b%29+%29&bg=ffffff&fg=545454&s=0&c=20201002) , and that this is best possible. I can only get the upper bound of
, and that this is best possible. I can only get the upper bound of  , and I am not sure how to establish the matching lower bound. Anyone have any thoughts on this?
, and I am not sure how to establish the matching lower bound. Anyone have any thoughts on this?
29 December, 2017 at 4:31 pm
Siddhartha Gadgil
I have written details. A reference is arXiv:0809.3110 (but I have not cited this).
29 December, 2017 at 6:19 pm
Terence Tao
Great! I’ve added the citation and corrected some small typos.
One consequence of our argument is that for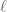 the minimal deficiency as constructed in your text, the quantity
the minimal deficiency as constructed in your text, the quantity  must be unbounded, however I cannot think off-hand of a simple example of a sequence of words
must be unbounded, however I cannot think off-hand of a simple example of a sequence of words  that exhibit this unboundedness. This can be extracted eventually from the proof of our main theorem, but I wonder if there is a simple example. I was at least able to find a short instance of non-homogeneity:
that exhibit this unboundedness. This can be extracted eventually from the proof of our main theorem, but I wonder if there is a simple example. I was at least able to find a short instance of non-homogeneity: ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=545454&s=0&c=20201002) has minimal deficiency 2, but
has minimal deficiency 2, but ![[a,b]^3](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%5E3&bg=ffffff&fg=545454&s=0&c=20201002) has minimal deficiency 4 (indeed, this latter fact is implicitly why we have our very first bound
has minimal deficiency 4 (indeed, this latter fact is implicitly why we have our very first bound ![\ell([a,b]) \leq 4/3](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ba%2Cb%5D%29+%5Cleq+4%2F3&bg=ffffff&fg=545454&s=0&c=20201002) for homogeneous length functions).
for homogeneous length functions).
30 December, 2017 at 8:00 pm
Terence Tao
Ah, I think I have the explicit demonstration of unboundedness of : I believe the word
: I believe the word ![[a^n,b^n]^2](https://s0.wp.com/latex.php?latex=%5Ba%5En%2Cb%5En%5D%5E2&bg=ffffff&fg=545454&s=0&c=20201002) has minimal deficiency
has minimal deficiency  , but
, but ![[a^n,b^n]^4](https://s0.wp.com/latex.php?latex=%5Ba%5En%2Cb%5En%5D%5E4&bg=ffffff&fg=545454&s=0&c=20201002) has minimal deficiency
has minimal deficiency  .
.
26 December, 2017 at 4:32 am
Apoorva Khare
I uploaded a revised version, small edits as promised. [And I am done for now.] In particular, for now I changed “To rectify the situation” to “In attempting to construct homogeneous length functions on F_2”. But of course, please feel free to still “majorly revise” if it improves the exposition.
Also, I took a look at the additive notation being used for \varphi at the end of the paper, and I think it is fine, since it takes values in the abelianization of G. Is there a problem here or (is additive notation being used) somewhere else?
26 December, 2017 at 5:45 pm
E. Ben-David
A simple observation: In Proposition 1.6. there is no need to assume that is a topological group and the map
is a topological group and the map  is continuous. Both these are immediate from (a)-(c). The proof follows from the fact that
is continuous. Both these are immediate from (a)-(c). The proof follows from the fact that  and the triangle inequality.
and the triangle inequality.
26 December, 2017 at 6:03 pm
Apoorva Khare
Thanks Emanuel! Indeed I had written “(topological)” in the very next line after the Proposition, for the reason that you mention. I’ll tell my co-author Bala of your comment, and change it in our paper [5] (and here as well).
26 December, 2017 at 7:46 pm
Apoorva Khare
I made some more edits – am done for now. Notably, the Main Proposition does not require assuming that the constant is non-negative, since this can be deduced from the hypotheses, see Remark 2.13. (But moreover, is this fact actually used in the proof?) I have added this and a “local” version of the Proposition, in Remark 2.13.
is non-negative, since this can be deduced from the hypotheses, see Remark 2.13. (But moreover, is this fact actually used in the proof?) I have added this and a “local” version of the Proposition, in Remark 2.13.
Other changes: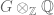 , corrected a couple of typos. I also added a footnote to perhaps clarify the (abundance of) notation in the paragraph; we can decide to remove it, retain it, or integrate it into the text; and of course, reword it.
, corrected a couple of typos. I also added a footnote to perhaps clarify the (abundance of) notation in the paragraph; we can decide to remove it, retain it, or integrate it into the text; and of course, reword it.
* Changed \backslash to \setminus globally.
* Removed “topological” to reword Proposition 1.6 and the subsequent sentence.
* Minor edit to the text after “Inserting this”, in the proof of the Splitting lemma, to clarify Pace’s recent observation.
* In defining
26 December, 2017 at 8:02 pm
Apoorva Khare
PS> Suppose is non-abelian, and we want a bound on
is non-abelian, and we want a bound on ![\ell([a,b])](https://s0.wp.com/latex.php?latex=%5Cell%28%5Ba%2Cb%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) as in the Main Proposition. Would it be (somewhat) related to consider how close one can get to the number 9 in the Proposition, for various classes of functions
as in the Main Proposition. Would it be (somewhat) related to consider how close one can get to the number 9 in the Proposition, for various classes of functions 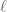 ? Stated via Remark 2.13, for length functions we get 0 instead of 9; and for homogeneous quasi-morphisms we get 3 (Section 4.2).
? Stated via Remark 2.13, for length functions we get 0 instead of 9; and for homogeneous quasi-morphisms we get 3 (Section 4.2).
27 December, 2017 at 6:25 am
Tobias Fritz
I’ve made some further edits to the draft. Let me also list the most significant ones, so that somebody else can take a look at this summary and double-check my edits if necessary.
* I’ve uniformized the notation of Proposition 1.6 with the rest of the paper.![\ell([x,y])](https://s0.wp.com/latex.php?latex=%5Cell%28%5Bx%2Cy%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) in terms of the subgroup
in terms of the subgroup  , since it was verbatim almost the same equation, and only expressed the idea in words.
, since it was verbatim almost the same equation, and only expressed the idea in words.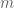 to be positive, since the argument that we make there would not work for negative
to be positive, since the argument that we make there would not work for negative 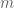 .
.
* Added some explanation of what ‘Kobayashi-type construction’ means (after consultation with Apoorva).
* Mention of the Ribe program is now at the very end of Sec 1.2.
* In Remark 2.13, I’ve removed the additional display giving the bound on
* In the first paragraph of Section 4, I’ve required
* In the final paragraph of Section 4.2, I’ve replaced ‘linear growth’ by homogeneous, and also rephrased the final sentence.
* In the second item after Proposition 4.5, I’ve added the factor of 2 that Terry was missing, and also included symmetry as another assumption.
* I’ve streamlined the argument in the last few paragraphs a bit and tried to clarify what we do there.
There’s one remaining \todo after Proposition 4.5, where (as Terry pointed out) we haven’t explained how to achieve the bound. My guess is word length with respect to conjugates of generators, but I haven’t thought hard about how to prove it. Does anyone know how to do this?
Otherwise, I’m personally quite happy with the paper now.
27 December, 2017 at 6:25 am
Tobias Fritz
Here’s a more abstract perspective on Theorem 1.2 that I’d like to mention in case that somebody else finds this enlightening as well. Consider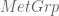 , the category of groups equipped with a pseudo-length function, where the morphisms are length-nonincreasing homomorphisms; and let
, the category of groups equipped with a pseudo-length function, where the morphisms are length-nonincreasing homomorphisms; and let  be the category of Banach spaces with linear maps of norm at most 1. Then the forgetful functor
be the category of Banach spaces with linear maps of norm at most 1. Then the forgetful functor 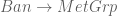 has a left adjoint that sends every group
has a left adjoint that sends every group  to the completion
to the completion ![\overline{G/[G,G]\otimes\mathbb{R}}](https://s0.wp.com/latex.php?latex=%5Coverline%7BG%2F%5BG%2CG%5D%5Cotimes%5Cmathbb%7BR%7D%7D&bg=ffffff&fg=545454&s=0&c=20201002) with respect to the pseudonorm induced from the pseudo-length function on
with respect to the pseudonorm induced from the pseudo-length function on  .
.![G \to\overline{G/[G,G]\otimes\mathbb{R}}](https://s0.wp.com/latex.php?latex=G+%5Cto%5Coverline%7BG%2F%5BG%2CG%5D%5Cotimes%5Cmathbb%7BR%7D%7D&bg=ffffff&fg=545454&s=0&c=20201002) is an isometric embedding if and only if the pseudo-length function on
is an isometric embedding if and only if the pseudo-length function on  is homogeneous.
is homogeneous.
What we’ve shown is that the unit of the adjunction
27 December, 2017 at 9:25 am
Apoorva Khare
This is a nice observation – and thanks also to Tobias for making the above changes.
I just now made 2-3 small changes, and also made the bibliography alphabetical. (I am done for now.) Once the remaining pending to-do is resolved — likely over the weekend — I am also happy with the paper.
28 December, 2017 at 5:35 am
sgadgil
I should clarify that by essentially sharp I meant up to constant, I believe 9 in this case.
29 December, 2017 at 3:39 pm
Lior Silberman
Sorry for staying out of the editing; getting dropbox to work on my idiosyncratic set-up would have been too much work. I really like the writing; a couple of remarks in case someone wants to put them in.
– Footnote 1: I think the word “length metric” should appear here somewhere.
– Remark 2.8: I wouldn’t say the observation is “superseded” by Theorem 1.2, since it is a component of its proof.
I’m thinking about “todo” example for Prop 4.5.
29 December, 2017 at 12:12 pm
Terence Tao
I’ve gone through the paper a final time. Except for the last issue of actually constructing a length function on the free group which is large on![[a^k,b^m]](https://s0.wp.com/latex.php?latex=%5Ba%5Ek%2Cb%5Em%5D&bg=ffffff&fg=545454&s=0&c=20201002) , I think we are basically ready to submit and put on the arXiv.
, I think we are basically ready to submit and put on the arXiv.
We haven’t yet discussed what journal to send the article to. A group theory journal might be appropriate, and the obvious one here would be the Journal of Group Theory. (The Journal of Algebra is Elsevier, which I am still boycotting.) I note that two of our references come from L’Enseignement
Math\’ematique (albeit from 20+ years ago); this journal does seem to have a somewhat geometric group theory nature to it, so it might also be a possibility. Somewhat more ambitious would be Algebra and Number Theory, but this journal is fairly selective. Anyone else have any suggestions or preferences?
29 December, 2017 at 4:26 pm
Siddhartha Gadgil
A couple of Journals where Geometric Group theory stuff appears are “Algebraic and Geometric Topology” (e.g. Peter Scott as corresponding editor) and “Geometria Dedicata”. Another is “Journal of Topology and Analysis”
29 December, 2017 at 8:43 pm
Yemon Choi
It is obviously up to those involved, but I find it a bit odd that people boycotting Elsevier seem relatively happy to submit to De Gruyter, who have long been no strangers to price-gouging, well-before the era of blogs.
Why not support one of the new-ish diamond-OA journals? Or something from the MSP stable?
29 December, 2017 at 8:56 pm
Terence Tao
Algebra & Number theory, which was another of my suggestions, is MSP. I did notice that J. Group Theory is de Gruyter, and this journal wasn’t my top choice, but it was the journal whose subject area most closely aligned with this specific paper, so I felt it should be mentioned as an option.
29 December, 2017 at 4:24 pm
Siddhartha Gadgil
I have written the final “todo” example and copied to Dropbox and thanks to everyone for the elegant writing (including greatly improving what I had written earlier).
29 December, 2017 at 4:56 pm
Siddhartha Gadgil
My apologies for being out of action for 4 days (especially not clarifying the todo example) – I was travelling without a laptop, and with spotty internet. Thanks again all for the elegant writing.
29 December, 2017 at 7:28 pm
Apoorva Khare
I’ve just completed a few minor edits (and am done for now), including adding journal/page-references to the recently added citation. The paper looks good now.
A quick question: can we make the font 11pt instead of 12pt unless people feel strongly for 12pt? (This would bring the pagecount down to 14, in case this matters for making the change or not.)
29 December, 2017 at 8:54 pm
Terence Tao
Sure, this is fine with me, though it may well be moot if the journal we end up submitting to has a house style.
29 December, 2017 at 9:19 pm
Apoorva Khare
Thank you – I have now changed the font size, and globally changed := to \coloneqq in all files (and spell-checked them too). Also: point taken journal house styles (though e.g. AMS journals have 11pt).
30 December, 2017 at 1:00 am
Tobias Fritz
And I’ve just removed the two drafting packages, showkeys and todo.
I can’t comment much on the journals discussion due to lack of knowledge of journals in this area.
1 January, 2018 at 10:45 am
Pace Nielsen
I gave the preprint another read-through and will make some minor typographical changes tonight, but had a few questions in the meantime.
1. Is there a reason we haven’t used the classification # 20F65? It seems like a good fit for our paper.
2. Is there a quick reference to the identity claimed in Example 1.4 for nilpotency class 2 groups? I am personally unfamiliar with this fact, and couldn’t find a proof by a quick google search. Or is it just really easy to prove and I just haven’t seen it yet?
3. Would people be okay with replacing the paragraph starting “In attempting to construct…” at the end of subsection 1.1 with something much shorter like: “Our initial attempts to construct homogeneous length functions on F_2 all failed in light of our main result. However, many of these methods work under minor weakenings of the hypotheses, such as working with monoids rather than groups, or weakening homogeneity. Results in these cases are discussed further in Section 4.”
4. In Remark 2.13 it says, parenthetically, “Equality is attained for Banach spaces.” I didn’t understand this sentence, as I haven’t seen any argument that the constant 9 has been optimized. Does this sentence need to be removed/modified?
1 January, 2018 at 11:40 am
Apoorva Khare
I am fine with both #1 and #3 either way (although I am not an expert in GGT, and hence will defer to more expert opinions).
Re: #4, I put that clause in to point out: here is an inequality, and if the reader is wondering whether it’s always strict, the answer is: no. I would have put in such a parenthetical remark even if the 9 was replaced by a better constant… because we present an inequality, and hence say whether or not it is strict. How would you propose to update this?
1 January, 2018 at 12:23 pm
Pace Nielsen
@Apoorva: Re #4: I think I see now what you were trying to say there, and the sentence is fine as it stands! However, we could instead say something like “If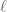 is a homogeneous pseudo-length function, then both sides are zero, so equality can hold.”
is a homogeneous pseudo-length function, then both sides are zero, so equality can hold.”
1 January, 2018 at 1:09 pm
Terence Tao
Ah, did not know about 20F65! Sure, we can add that to the classification. #3 is also fine with me.
For #2, this follows from the fact that the commutator map![(g,h) \mapsto [g,h]](https://s0.wp.com/latex.php?latex=%28g%2Ch%29+%5Cmapsto+%5Bg%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) is a bihomorphism from
is a bihomorphism from  to
to ![[G,G]](https://s0.wp.com/latex.php?latex=%5BG%2CG%5D&bg=ffffff&fg=545454&s=0&c=20201002) for nilpotent groups of nilpotency class two (see e.g. https://math.stackexchange.com/questions/1970022/commutator-in-nilpotent-group-of-class-2-is-bilinear , I do not know of a more formal reference but presumably it would likely be in any basic group theory text). The way I think of it is that every time one tries to interchange
for nilpotent groups of nilpotency class two (see e.g. https://math.stackexchange.com/questions/1970022/commutator-in-nilpotent-group-of-class-2-is-bilinear , I do not know of a more formal reference but presumably it would likely be in any basic group theory text). The way I think of it is that every time one tries to interchange 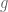 and
and 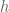 one creates a factor of
one creates a factor of ![[g,h]](https://s0.wp.com/latex.php?latex=%5Bg%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) somewhere, so if one wishes to interchange
somewhere, so if one wishes to interchange  with
with 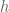 one creates factors of
one creates factors of ![[g_1,h]](https://s0.wp.com/latex.php?latex=%5Bg_1%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) and
and ![[g_2,h]](https://s0.wp.com/latex.php?latex=%5Bg_2%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) . These factors are in different locations (leading to the identity
. These factors are in different locations (leading to the identity ![[g_1 g_2,h] = [g_2,h]^{g_1} [g_1,h]](https://s0.wp.com/latex.php?latex=%5Bg_1+g_2%2Ch%5D+%3D+%5Bg_2%2Ch%5D%5E%7Bg_1%7D+%5Bg_1%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) in general) but in the nilpotency class 2 case, all commutators are central and so we conclude that
in general) but in the nilpotency class 2 case, all commutators are central and so we conclude that ![g \mapsto [g,h]](https://s0.wp.com/latex.php?latex=g+%5Cmapsto+%5Bg%2Ch%5D&bg=ffffff&fg=545454&s=0&c=20201002) is a homomorphism. It’s also instructive to work things out explicitly in the case of the Heisenberg group.
is a homomorphism. It’s also instructive to work things out explicitly in the case of the Heisenberg group.
1 January, 2018 at 6:59 pm
Apoorva Khare
A few edits from me (and I’m done for now). The following additions might probably benefit from a little polishing, please check:
* Page 2: I added one line about the bihomomorphism to the Heisenberg group remark.
* Page 10: Added one sentence preceding Remark 3.1.
* Page 7: Added a sentence at the end. Essentially, our main proposition is in terms of a constant , and I think we should observe (here in this Remark — or earlier? Or both?) that the only way to get
, and I think we should observe (here in this Remark — or earlier? Or both?) that the only way to get 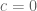 is for Banach spaces. [I also slightly updated the sentence “(Both sides are…)”.]
is for Banach spaces. [I also slightly updated the sentence “(Both sides are…)”.]
2 January, 2018 at 3:31 am
Tobias Fritz
Looks good to me, except for the new sentence on p.7 (at the end of Remark 2.13), which had the minor issue that embedding the torsion-free abelianization of into a Banach space will only yield those
into a Banach space will only yield those 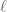 that are strictly positive on nontrivial elements of that torsion-free abelianization. So I’ve rephrased this in terms of group homomorphisms to Banach spaces. (If somebody can think of a better formulation, please go ahead.)
that are strictly positive on nontrivial elements of that torsion-free abelianization. So I’ve rephrased this in terms of group homomorphisms to Banach spaces. (If somebody can think of a better formulation, please go ahead.)
I’ve also removed most of our comments in the source code in order to prepare for arXiv upload.
I really like how the new sentence before Remark 3.1 is phrased: those readers who know enough category theory will understand it immediately as a precise statement with formal meaning, while those readers who don’t will instead take it as a vague intuitive explanation.
2 January, 2018 at 2:19 pm
Apoorva Khare
Here’s a quick question, possibly regarding that pesky factor 9: since we’re going to work with asymptotic multiples anyways, what if we replace our “super-additivity” in the main Proposition (see Equation (2.3)) by
\ell(x^k) \geq k \ell(x) – c
for a larger value of k than 2? Recall by e.g. our reference [9] (or maybe [6] as well) that for c=0 this is also equivalent to the case k=2 for any length function; and hence guarantees homogeneity.
Thus, I think the proof of the Main Proposition should still go through with the changed assumption above (but it is 3:45am here), and I am wondering if we would get a smaller factor f(k), where f(2)=9? Or do things actually get worse…
2 January, 2018 at 2:30 pm
Apoorva Khare
PS. A slight quantitative refinement: why not consider in fuller generality, the inequality
instead of using the same constant , and with general
, and with general 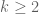 .
.
2 January, 2018 at 7:15 pm
Apoorva Khare
I think the use of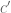 is fine, but the inequality for
is fine, but the inequality for  is too strong/rigid/tight as is… Replacing
is too strong/rigid/tight as is… Replacing 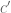 by
by  might be better. So perhaps my broader question is, what is the “correct regime” for the lower bound on
might be better. So perhaps my broader question is, what is the “correct regime” for the lower bound on 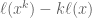 . I didn’t verify, but offhand it appears to be linear in
. I didn’t verify, but offhand it appears to be linear in  ?
?
2 January, 2018 at 7:22 pm
sgadgil
As in the original case (c=0), induction gives a condition for powers of 2, given the condition for squares. Also, by the triangle inequality (which is coarse in this case), a bound for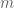 gives one for
gives one for  .. Hence we get a bound for all
.. Hence we get a bound for all  given the square condition.
given the square condition.
From an expository point of view, I feel we should stick to square. Also a constant such as 9 I feel is inevitable given the quantifiers, we should just make sure there is no statement that suggests this constant is 1.
2 January, 2018 at 7:57 pm
Apoorva Khare
For exposition etc., I am perfectly happy to stick to square. My explorations were in order to understand just how much “additive leeway” our length function is allowed, and still yield the desired bound for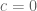 . And of course, to check where else length functions with just so much leeway occur.
. And of course, to check where else length functions with just so much leeway occur.
4 January, 2018 at 7:26 am
Apoorva Khare
I made a few changes. The most notable change is that given the “morally separate” bounds for sub-additivity and doubling of the length function, there is no reason to use the same bound in Equations (2.2) and (2.3). So I reworked the entire proof using two different constants. It wasn’t difficult to redo, but it would be nice if someone could double-check this section for completeness.
in Equations (2.2) and (2.3). So I reworked the entire proof using two different constants. It wasn’t difficult to redo, but it would be nice if someone could double-check this section for completeness.
A couple of other points: first, in (what is now) Remark 2.14, I had written expressions like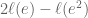 , where
, where  denotes the identity in
denotes the identity in  . But then
. But then 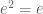 ! So I have updated that slightly. Please feel free to reword or trim.
! So I have updated that slightly. Please feel free to reword or trim.
Second, I introduced Remark 2.13 to address the question I’d raised earlier, after discussing it with Siddhartha Gadgil. The point is that we don’t gain anything compared to the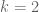 case.
case.
Finally, I didn’t update the (final) Section 4 in light of the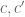 update – I think most of the section remains unchanged, but Proposition 4.5 needs updating of course. So please can someone do the needful, thank you.
update – I think most of the section remains unchanged, but Proposition 4.5 needs updating of course. So please can someone do the needful, thank you.
4 January, 2018 at 8:32 am
Pace Nielsen
I quickly double-checked it and it looked good to me.
I would recommend changing both instances of to the words “for each”. (In general, in a paper, one should use the words rather than the symbols, especially in inline text.)
to the words “for each”. (In general, in a paper, one should use the words rather than the symbols, especially in inline text.)
4 January, 2018 at 9:26 am
Apoorva Khare
That sounds good to me, @Pace. When someone edits the last subsection, please can you make these two changes as well, thank you.
4 January, 2018 at 10:13 am
Terence Tao
I’ve made the changes and also updated the remarks section with the new constants (e.g. the commutator bound for quasimorphisms now has a bound of 4 rather than 9, getting closer to Bavard’s bound of 3).
4 January, 2018 at 10:30 am
Apoorva Khare
Great! In that case, perhaps a”pre-baby step” might be to check if our proof can be slightly upgraded to reduce our 4 to 3 as well (maybe also assuming that the defect of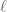 is bounded?). My guess being that if we combine some of the intermediate lemmas, we may be able to get closer to 3. (Of course, I’ll add that I am happy to stop at the present point as well.)
is bounded?). My guess being that if we combine some of the intermediate lemmas, we may be able to get closer to 3. (Of course, I’ll add that I am happy to stop at the present point as well.)
4 January, 2018 at 10:01 am
Apoorva Khare
Here’s one more question one might want to ponder: are the constants 4,5 in the “Main Proposition” optimal? Of course for the given “length” problem this doesn’t matter, but it does for “quasi-lengths”. In this case, a baby step is to first ask if the “Approximate conjugation invariance” = Lemma 2.7 has sharp constants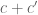 . One checks explicitly in its proof that
. One checks explicitly in its proof that
So the question here is: for each integer , can one find a group and a function
, can one find a group and a function 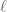 that satisfies this inequality with equality, where
that satisfies this inequality with equality, where 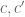 are precisely the suprema in Equation (2.15) ?
are precisely the suprema in Equation (2.15) ?
5 January, 2018 at 9:03 am
Apoorva Khare
Also, are there any connections to cancellative semigroups that we may want to elaborate upon? E.g., note that the free monoid on two generators (with the bi-invariant homogeneous metric that we mention) is cancellative. Can we show that it does not embed into any group?
5 January, 2018 at 9:12 am
Pace Nielsen
The free monoid on two generators embeds naturally into the free group on two generators (sending generators to generators). Perhaps I’m misunderstanding your question?
5 January, 2018 at 9:19 am
Apoorva Khare
Ah that’s right, and I see that’s all that is required for the cancellation property. Somehow, I thought of that but was seeking a metric on F_2 for which we get an *isometric* embedding. But of course, that’s a separate question than the embedding problem for cancellative semigroups.
5 January, 2018 at 10:00 am
Apoorva Khare
Or rather, it’s the embedding question in a smaller category: that of cancellative *metric* semigroups. The point is that the free monoid on any set with at least two elements…
* does embed in the category of (cancellative semigroups + semigroup maps as morphisms) — into the free group on the same generating set (as Pace said); and
* does not embed into any object, in the category of (cancellative metric semigroups with bi- invariant metrics + isometric semigroup maps as morphisms).
Now since I was talking about embedding the semigroup, I thought to not touch the morphism part, and only change the category to the intermediate one: cancellative metric semigroups. Hence my question.
5 January, 2018 at 10:06 am
Apoorva Khare
PS. Again, oops. I meant *homogeneous length functions* when I said “bi-invariant metrics” in the “does not embed” part. But then, perhaps my question does have an answer? Namely, is it true that the bi-invariant metric on FreeGroup(X) (= smallest length in terms of X, their inverses, and *all their* conjugates) extends the metric on FreeMonoid(X) that we mention?
7 January, 2018 at 6:09 am
Apoorva Khare
Following some discussions with Tobias, I’ve added “footnote 4” on page 11 (and am done for now). Of course, I am not an expert on quasi-morphims, so if someone could please improve (and perhaps relocate) it, that would be great.
7 January, 2018 at 6:14 am
Tobias Fritz
I’m not an expert on quasi-morphisms either, but it looks good to me!
7 January, 2018 at 10:01 am
Apoorva Khare
I heard from both Tobias and Siddhartha about my footnote 4 being fine. Siddhartha also explained to me the solution to my question about the bi-invariant metrics in the free monoid vs. free group. So I now plan to add a few remarks, and share with everyone.
If someone is editing the file, please let me know at khare @ iisc.ac.in and I can not even start editing.
7 January, 2018 at 1:37 pm
Apoorva Khare
I have now completed my edits – they are in blue on pages 10, 11, 12, 14, including the footnote previously added “today”. As Siddhartha explained, the non-crossing matchings and minimal deficiency show up in the proof of Proposition 4.1 now, which is before their previous location; thus I moved that exposition up (this explains the edits on page 14). To conclude, here’s my standard disclaimer: please feel free to reword, relocate, or even undo these edits if the new additions are felt to be removable. [And yes: once these edits are incorporated, I am – once more! – happy with the paper.]
7 January, 2018 at 1:49 pm
Apoorva Khare
Sorry, I am now done, after making a couple of small edits.
8 January, 2018 at 6:29 am
Apoorva Khare
After inputs from Siddhartha Gadgil, I added reference [3] by de Bruijn and Erdos, which is cited on page 12 (in blue, just after Equation (4.2)) and on page 15, also in blue. The point is that if the length is sub-additive, then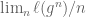 exists for all
exists for all 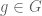 . Else, one may need to take
. Else, one may need to take 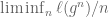 if there is an additive error in the length — which is indeed the case on pages 12 and 15. However, this can be bypassed if the error is not too large, as shown by de Bruijn and Erdos in the added reference.
if there is an additive error in the length — which is indeed the case on pages 12 and 15. However, this can be bypassed if the error is not too large, as shown by de Bruijn and Erdos in the added reference.
I also updated the blue text slightly, since the analysis in the free group
analysis in the free group 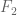 is not needed in the proof of Proposition 4.1, and hence I moved it to page 14. And I made a few more edits in the blue text.
is not needed in the proof of Proposition 4.1, and hence I moved it to page 14. And I made a few more edits in the blue text.
Once again, I am done (for now). Siddhartha was also fine with the text, so if someone wants to further edit it, please can you remove the blue during the polishing, thanks.
10 January, 2018 at 5:50 am
Anonymous
I am reading the draft of the paper. Certainly Equation (2.3) should be crucial to establish Proposition 2.1. But in the paper it is not clear where it’s been used. I don’t think it is required for either Lemma 2.9 (Splitting lemma) or Corollary 2.11. It’d be helpful to clarify this.
10 January, 2018 at 6:15 am
Apoorva Khare
Thanks – I think it is used to derive Equation (2.6), which is used in proving Lemma 2.7, which gets used in the Splitting lemma as well as Corollary 2.11. (And (2.6) is also used in the final proof.)
10 January, 2018 at 8:00 am
Terence Tao
Sorry I didn’t respond for a while, I am travelling currently. It’s looking like the writing process has neared its conclusion. If I don’t hear for any more major changes, I will upload the paper to the arXiv tomorrow. (There will of course still be a chance to revise the arXiv version should the need arise.)
We didn’t reach much of a conclusion for journals. One suggestion made to me was the Proceedings of the AMS, which is a good generalist journal publishing shortish papers like ours. Presumably Pham Huu Tiep would the editor closest to the paper topic. (He’s also an editor at Algebra & Number Theory, but presumably if he thinks that journal would be even more suitable he would tell us.) What does everyone think about this choice? We can submit somewhat after the arXiv preprint goes up, of course.
p.s. in preparation for arXiv’ing, I have combined all the working .tex files for the paper into a single file (linear.tex).
10 January, 2018 at 8:42 am
Apoorva Khare
I like Terry’s idea of asking Pham Huu Tiep whether A&NT or Proc. AMS would be a reasonable match.
Also, to be extremely pedantic, a couple of minutes ago in “introduction.tex”, I changed a string in Proposition 1.7(2) from to
to 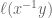 — since this is the convention in Section 1 paragraph 1. I didn’t realize Terry was editing, so perhaps he could make this change in linear.tex before uploading to arXiv. Thanks.
— since this is the convention in Section 1 paragraph 1. I didn’t realize Terry was editing, so perhaps he could make this change in linear.tex before uploading to arXiv. Thanks.
10 January, 2018 at 8:53 am
Terence Tao
OK, I’ll do that after arXiving the paper tomorrow if nobody objects. I’m done editing the paper, so feel free to make the last final edits.
Best,
Terry
11 January, 2018 at 5:19 am
Terence Tao
Due to spotty internet access (I’m travelling right now) I’ve asked Apoorva to handle the arXiv submission. In other news, I talked with Tim Gowers and Gil Kalai and they are happy to have our project retroactively designated as Polymath13 (which presumably will not be “unlucky” for us :).
11 January, 2018 at 7:00 am
nicodean
I thought the Intransitive dice-project was polymath13?
11 January, 2018 at 5:05 pm
Terence Tao
Good point – for some reason a wiki page was never created for that project. I’ve put one in now, and renumbered this project as Polymath14.
11 January, 2018 at 11:30 am
Lior Silberman
The project on intransitive dice has already been sometimes designated “Polymath 13” — see for example Gil’s post on the polymath blog.
10 January, 2018 at 10:13 am
Pace Nielsen
I also agree with Terry’s idea. I’d favor A&NT first if that agrees with the editor’s thoughts.
10 January, 2018 at 10:50 am
Apoorva Khare
Seconded, @Pace. Also, I am now done with my “final edits”.
10 January, 2018 at 4:46 pm
Lior Silberman
Second posting to the arXiv now. I’m happy with either journal (or any other).
11 January, 2018 at 6:01 am
Apoorva Khare
As Terry said, I will submit to arXiv later tonight. I took a look at the math categories at this link and wonder if the following cross-listings are fine:
1. Primary: Metric Geometry
2. Secondary: Group Theory, Functional Analysis (since Banach spaces feature).
3. I debated between which of MG and GT should be primary and which should be secondary. If anyone wants to reverse the order or suggest other changes, please let me know.
4. I wasn’t planning to cross-list to Probability or Category Theory, even though a motivation and the final step are probabilistic… Again, if people prefer I should change this (or add any other categories), please let me know. We still have a few hours before tomorrow’s cutoff.
11 January, 2018 at 6:29 am
sgadgil
As far as I know (I searched a little to check), combinatorial group theory papers are usually posted in math.GR with math.GT (GT = Geometric Topology) as secondary for those that have a geometric flavour – those that are really geometric group theory may reverse the order. Metric geometry is generally secondary.
11 January, 2018 at 6:40 am
Apoorva Khare
Ah ok, a typo by me: I meant to say GR and not GT.
Ok so primary = GR, secondary = MG, FA. Do we also add GT, which I hadn’t even suggested? (I’m assuming Prob or Category Theory are a “no” as per Siddhartha.)
11 January, 2018 at 7:08 am
sgadgil
I would say yes to GT – the tradition is that this is a very broad category to which a lot of people subscribe and group theory with a non-trivial ggt flavour gets cross-listed here
11 January, 2018 at 9:10 am
Tobias Fritz
Sounds great, thank you!
11 January, 2018 at 9:09 am
Apoorva Khare
My apologies for the multiple comments here: I just realized we don’t have keywords! I’m going to add the following keywords, say in about half an hour; and as Terry said, if updates are needed then we can make those in the next version.
* homogeneous length function
* pseudo-length function
* quasi-morphism
* Banach space embedding
Also, I am not adding “commutator length” as a keyword for now. I also won’t add a date, in keeping with previous Polymath preprints on the arXiv. If people have edits to suggest then please let me know.
11 January, 2018 at 11:32 am
Lior Silberman
One more typo: in the proof of Thm 4.3, we pull back to the free group generated two symbols, not to a formal group.
11 January, 2018 at 8:01 pm
Apoorva Khare
The Polymath14 paper is now up on the arXiv, at 1801.03908. Also, I made the change that Lior suggested, in the latest version on Dropbox. This version can be used for submission, and eventually we’ll update the arXiv version too.
11 January, 2018 at 9:05 pm
Homogeneous length functions on groups | What's new
[…] good bounds on quantities such as , until one can show that such norms have to vanish. See the previous post for a full proof. The result is robust in that it allows for some loss in the triangle inequality […]
25 January, 2018 at 10:27 pm
Spontaneous Polymath 14 – A success! | The polymath blog
[…] problem was posed by Apoorva Khare was presented and discussed and openly and collectively solved. (And the […]