Define the Collatz map on the natural numbers
by setting
to equal
when
is odd and
when
is even, and let
denote the forward Collatz orbit of
. The notorious Collatz conjecture asserts that
for all
. Equivalently, if we define the backwards Collatz orbit
to be all the natural numbers
that encounter
in their forward Collatz orbit, then the Collatz conjecture asserts that
. As a partial result towards this latter statement, Krasikov and Lagarias in 2003 established the bound
for all and
. (This improved upon previous values of
obtained by Applegate and Lagarias in 1995,
by Applegate and Lagarias in 1995 by a different method,
by Wirsching in 1993,
by Krasikov in 1989,
by Sander in 1990, and some
by Crandall in 1978.) This is still the largest value of
for which (1) has been established. Of course, the Collatz conjecture would imply that we can take
equal to
, which is the assertion that a positive density set of natural numbers obeys the Collatz conjecture. This is not yet established, although the results in my previous paper do at least imply that a positive density set of natural numbers iterates to an (explicitly computable) bounded set, so in principle the
case of (1) could now be verified by an (enormous) finite computation in which one verifies that every number in this explicit bounded set iterates to
. In this post I would like to record a possible alternate route to this problem that depends on the distribution of a certain family of random variables that appeared in my previous paper, that I called Syracuse random variables.
Definition 1 (Syracuse random variables) For any natural number
, a Syracuse random variable
on the cyclic group
is defined as a random variable of the form
where
are independent copies of a geometric random variable
on the natural numbers with mean
, thus
} for
. In (2) the arithmetic is performed in the ring
.
Thus for instance
and so forth. After reversing the labeling of the , one could also view
as the mod
reduction of a
-adic random variable
The probability density function of the Syracuse random variable can be explicitly computed by a recursive formula (see Lemma 1.12 of my previous paper). For instance, when
,
is equal to
for
respectively, while when
,
is equal to
when respectively.
The relationship of these random variables to the Collatz problem can be explained as follows. Let denote the odd natural numbers, and define the Syracuse map
by
where the –valuation
is the number of times
divides
. We can define the forward orbit
and backward orbit
of the Syracuse map as before. It is not difficult to then see that the Collatz conjecture is equivalent to the assertion
, and that the assertion (1) for a given
is equivalent to the assertion
for all , where
is now understood to range over odd natural numbers. A brief calculation then shows that for any odd natural number
and natural number
, one has
where the natural numbers are defined by the formula
so in particular
Heuristically, one expects the -valuation
of a typical odd number
to be approximately distributed according to the geometric distribution
, so one therefore expects the residue class
to be distributed approximately according to the random variable
.
The Syracuse random variables will always avoid multiples of three (this reflects the fact that
is never a multiple of three), but attains any non-multiple of three in
with positive probability. For any natural number
, set
Equivalently, is the greatest quantity for which we have the inequality
for all integers not divisible by three, where
is the set of all tuples
for which
Thus for instance ,
, and
. On the other hand, since all the probabilities
sum to
as
ranges over the non-multiples of
, we have the trivial upper bound
There is also an easy submultiplicativity result:
Lemma 2 For any natural numbers
, we have
Proof: Let be an integer not divisible by
, then by (4) we have
If we let denote the set of tuples
that can be formed from the tuples in
by deleting the final component
from each tuple, then we have
with an integer not divisible by three. By definition of
and a relabeling, we then have
for all . For such tuples we then have
so that . Since
for each , the claim follows.
From this lemma we see that for some absolute constant
. Heuristically, we expect the Syracuse random variables to be somewhat approximately equidistributed amongst the multiples of
(in Proposition 1.4 of my previous paper I prove a fine scale mixing result that supports this heuristic). As a consequence it is natural to conjecture that
. I cannot prove this, but I can show that this conjecture would imply that we can take the exponent
in (1), (3) arbitrarily close to one:
Proposition 3 Suppose that
(that is to say,
as
). Then
as
, or equivalently
I prove this proposition below the fold. A variant of the argument shows that for any value of , (1), (3) holds whenever
, where
is an explicitly computable function with
as
. In principle, one could then improve the Krasikov-Lagarias result
by getting a sufficiently good upper bound on
, which is in principle achievable numerically (note for instance that Lemma 2 implies the bound
for any
, since
for any
).
— 1. Proof of proposition —
Assume . Let
be sufficiently small, and let
be sufficiently large depending on
. We first establish the following proposition, that shows that elements in a certain residue class have a lot of Syracuse preimages:
Proposition 4 There exists a residue class of
with the property that for all integers
in this class, and all non-negative integers
, there exist natural numbers
with
and
and at least
tuples
obeying the additional properties
Proof: We begin with the base case . By (4) and the hypothesis
, we see that
for all integers not divisible by
. Let
denote the tuples
in
that obey the additional regularity hypotheses
for all ,note that this implies in particular the
case of (7). From the Chernoff inequality (noting that the geometric random variable
has mean
) and the union bound we have
for an absolute constant (where we use the periodicity of
in
to define
for
by abuse of notation). Hence by the pigeonhole principle we can find a residue class
not divisible by
such that
and hence by the triangle inequality we have
for all in this residue class.
Henceforth is assumed to be an element of this residue class. For
, we see from (8)
hence by the pigeonhole principle there exists (so in particular
) such that
so the number of summands here is at least . This establishes the base case
.
Now suppose inductively that , and that the claim has already been proven for
. By induction hypothesis, there exists natural numbers
with
(which in particular imply that ) and at least
tuples
obeying the additional properties
and (7) for all .
For each tuple (10), we may write (as in the proof of Lemma 2)
for some integers . We claim that these integers lie in distinct residue classes modulo
where
Indeed, suppose that for two tuples
,
of the above form. Then
(where we now invert in the ring
), or equivalently
By (11), (7), all the summands on the left-hand side are natural numbers of size , hence the sum also has this size; similarly for the right-hand side. From the estimates of
, we thus see that both sides are natural numbers between
and
, by hypothesis on
. Thus we may remove the modular constraint and conclude that
and then a routine induction (see Lemma 6.2 of my paper) shows that . This establishes the claim.
As a corollary, we see that every residue class modulo contains
of the at most. Since there were at least
tuples
to begin with, we may therefore forbid up to
residue classes modulo
, and still have
surviving tuples
with the property that
avoids all the forbidden classes.
Let be one of the tuples (10). By the hypothesis
, we have
Let denote the set of tuples
with the additional property
for all , then by the Chernoff bound we have
for some absolute constant . Thus, by the Markov inequality, by forbidding up to
classes, we may ensure that
and hence
We thus have
where run over all tuples with
being one of the previously surviving tuples, and
. By (11) we may rearrange this a little as
By construction, we have
for any tuple in the above sum, hence by the pigeonhole principle we may find an integer
In particular the number of summands is at least . Also observe from (13), (12) that
so in particular
It is a routine matter to verify that all tuples in this sum lie in and obeys the requirements (6), (7), closing the induction hypothesis.
Corollary 5 For all
in the residue class from the previous proposition, and all
, we have
In particular, we have
as
.
Proof: For every tuple in the previous proposition, we have
for some integer . As before, all these integers
are distinct, and have magnitude
From construction we also have , so that
. The number of tuples is at least
which can be computed from the properties of to be of size at least
. This gives the first claim, and the second claim follows by taking
to be the first integer for which
.
To conclude the proof of Proposition 3, it thus suffices to show that
Lemma 6 Every residue class
has a non-trivial intersection with
.
Indeed, if we let be the residue class from the preceding propositions, and use this lemma to produce an element
of
that lies in this class, then from the inclusion
we obtain (3) with
, and then on sending
to zero we obtain the claim.
Proof: An easy induction (based on first establishing that for all natural numbers
) shows that the powers of two modulo
occupy every residue class not divisible by
. From this we can locate an integer
in
of the form
. Since
, the claim follows.
We remark that the same argument in fact shows (assuming of course) that
in the limit for any natural number
not divisible by three.

96 comments
Comments feed for this article
25 January, 2020 at 8:14 pm
Anonymous
Is it possible to extend proposition 3 for each given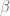 to find the explicit expression of the best possible
to find the explicit expression of the best possible 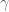 as a function of each given
as a function of each given 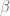 ?
?
26 January, 2020 at 9:11 am
Terence Tao
The argument I give in this post does give in principle an explicit way to convert a specific value of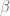 to a specific value of
to a specific value of 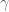 , but it is quite inefficient and would not give the best possible
, but it is quite inefficient and would not give the best possible 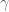 . Heuristically one can obtain a relationship as follows. From (5) we have for any natural number
. Heuristically one can obtain a relationship as follows. From (5) we have for any natural number  not divisible by 3 that
not divisible by 3 that
The law of large numbers suggests that typically one has . (Making this intuition precise is in fact a bit tricky, and is the reason why the arguments in the post are rather technical and lead to inefficiencies in converting from
. (Making this intuition precise is in fact a bit tricky, and is the reason why the arguments in the post are rather technical and lead to inefficiencies in converting from 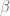 values to
values to 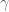 values.) If one blindly inserts this law of large number approximation, we see that
values.) If one blindly inserts this law of large number approximation, we see that
This basically tells us that (or
(or 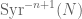 ) has
) has 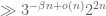 preimages, each of which have size about
preimages, each of which have size about 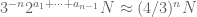 by the equation just after (3). (A good rule of thumb is that each iterate of the Syracuse map tends to reduce the magnitude by about 3/4 on the average.) Applying this heuristic to
by the equation just after (3). (A good rule of thumb is that each iterate of the Syracuse map tends to reduce the magnitude by about 3/4 on the average.) Applying this heuristic to  , and setting
, and setting  , we then arrive at a predicted value of
, we then arrive at a predicted value of 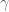 given by
given by
or equivalently
or
If we take this numerology as the value of the best in principle value of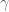 one can get for a given
one can get for a given 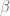 , this argument would need
, this argument would need 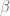 to be less than
to be less than 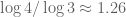 to get a nontrivial bound for
to get a nontrivial bound for 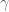 , and less than
, and less than 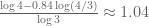 to improve upon Krasikov-Lagarias. (For comparison, the inequality
to improve upon Krasikov-Lagarias. (For comparison, the inequality 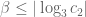 gives an upper bound for
gives an upper bound for 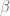 of
of 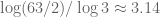 ; this can presumably be improved upon substantially, but clearly there is a gap to close here. Perhaps a computation of
; this can presumably be improved upon substantially, but clearly there is a gap to close here. Perhaps a computation of 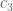 and
and 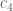 would shed some more light on the situation.) However if one wishes to get a better numerical value of
would shed some more light on the situation.) However if one wishes to get a better numerical value of  , it may be possible to work with a more complicated quantity than
, it may be possible to work with a more complicated quantity than 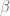 , taking into account the entire distribution of the Syracuse random variable and not just the infimal value of the distribution function. (In some sense this is what Krasikov and Lagarias actually do, though not quite in this language.)
, taking into account the entire distribution of the Syracuse random variable and not just the infimal value of the distribution function. (In some sense this is what Krasikov and Lagarias actually do, though not quite in this language.)
26 January, 2020 at 11:33 am
Uwe Stroinski
Instead of computing the for large
for large  exactly it might be sufficient to lower bound the numerator by
exactly it might be sufficient to lower bound the numerator by 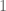 and to work out the denominator with your recursive formula.
and to work out the denominator with your recursive formula.
26 January, 2020 at 12:06 pm
Terence Tao
The denominator unfortunately grows quite fast: the worst case is that the denominator for is
is  , though already for
, though already for 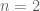 there is a little bit of cancellation and the final denominator ends up being
there is a little bit of cancellation and the final denominator ends up being 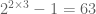 rather than
rather than 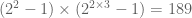 . My feeling is that while it is technically true that the probability densities are rational numbers, by the time
. My feeling is that while it is technically true that the probability densities are rational numbers, by the time  gets even moderately large (e.g.,
gets even moderately large (e.g., 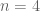 ) it is better off thinking of them as being generic real numbers.
) it is better off thinking of them as being generic real numbers.
25 January, 2020 at 10:33 pm
Anonymous
The inequality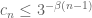 (given below proposition 3) seems to imply an upper (not lower!) bound on
(given below proposition 3) seems to imply an upper (not lower!) bound on 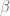 .
.
[Corrected, thanks – T.]
26 January, 2020 at 7:36 am
Jeff
Mistakes like these tend to come from fatigue. And they tend to artificially bolster one’s confidence, especially if the subject is integral to one’s philosophical gestalt.
Taking a break is a good thing. Take care! Best wishes.
26 January, 2020 at 1:47 am
Anonymous
Wow, very exciting result. I am just wondering, can you make o(1) arbitrarily small, meaning that o(1) goes to 0 and thus having the collatz conjecture settled?
26 January, 2020 at 9:20 am
Terence Tao
Not with the current argument, but I would imagine that the limit of the method would be to show that the preimage of any given number not divisible by 3 has positive density (so the
not divisible by 3 has positive density (so the  error would be replaced by an constant depending only on
error would be replaced by an constant depending only on  ). Note that my previous paper already shows that a positive proportion of all orbits reach a bounded value, so by the pigeonhole principle there is at least one number
). Note that my previous paper already shows that a positive proportion of all orbits reach a bounded value, so by the pigeonhole principle there is at least one number  whose preimage has positive density.
whose preimage has positive density.
As I stated in the previous post, the full Collatz conjecture is still well out of reach of current methods (though Alex Kontorovich has recently pointed out that there is a remote possibility that one could perhaps engineer a counterexample to the conjecture if one could somehow demonstrate enough “Turing completeness” to the iteration). However, partial results such as these can still give various worthwhile insights on the nature of the problem and its connection to other questions, even if this is not sufficient to lead to a full resolution of the problem. For instance these arguments seem to indicate that the 3-adic structure of the Collatz iteration (as captured by the Syracuse random variables ) should be studied further, particularly for statistical versions of the Collatz conjecture (in which one is primarily focused on controlling the behaviour of “typical” orbits rather than _all_ orbits); previous work has focused more on the 2-adic structure than the 3-adic (and perhaps ultimately the two need to somehow be combined, though how to do so is still beyond our current technology). Related to this, these arguments also highlight the fact that the Syracuse map
) should be studied further, particularly for statistical versions of the Collatz conjecture (in which one is primarily focused on controlling the behaviour of “typical” orbits rather than _all_ orbits); previous work has focused more on the 2-adic structure than the 3-adic (and perhaps ultimately the two need to somehow be combined, though how to do so is still beyond our current technology). Related to this, these arguments also highlight the fact that the Syracuse map  is better suited than the Collatz map
is better suited than the Collatz map  (or the standard acceleration
(or the standard acceleration  ) for studying the 3-adic structure (this is basically because each application of
) for studying the 3-adic structure (this is basically because each application of  contains precisely one multiplication by 3 and a variable number of divisions by
contains precisely one multiplication by 3 and a variable number of divisions by 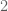 , in contrast for instance to
, in contrast for instance to  that contains exactly one division by 2 but a variable number of multiplications by
that contains exactly one division by 2 but a variable number of multiplications by  ). As I previously mentioned, I think it will also be instructive to see how these results depend on the precise parameters of the Collatz-type iteration one is studying (e.g., if one replaces
). As I previously mentioned, I think it will also be instructive to see how these results depend on the precise parameters of the Collatz-type iteration one is studying (e.g., if one replaces 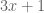 with some other affine form).
with some other affine form).
26 January, 2020 at 9:41 am
Jeff
It may help if you define positive density. Do you mean positive ‘natural’ density. I think you are confusing natural density with some other one.
26 January, 2020 at 12:03 pm
Terence Tao
The arguments in my paper currently apply to logarithmic density, but I believe this is mainly a technical restriction and that with some additional work they can be upgraded to natural density (I believe someone is looking into this question right now); see Remarks 1.4 and 1.16 of my paper.
More generally, it is often the case in analytic number theory problems that an easier result in logarithmic density (or sometimes Dirichlet density) is established first, with the harder natural density result coming later, so it makes sense to focus first on the logarithmic density problem to get some initial results, basically because the logarithmic density enjoys some approximate multiplicative invariance properties that natural density lacks. (For instance, the fact that the set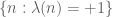 of numbers that are the product of an even number of primes has logarithmic density 1/2 can be proven in an elementary half-page argument, but to get natural density 1/2 is equivalent to the prime number theorem. The fact that
of numbers that are the product of an even number of primes has logarithmic density 1/2 can be proven in an elementary half-page argument, but to get natural density 1/2 is equivalent to the prime number theorem. The fact that  has logarithmic density 1/4 was only established in 2015, but the natural density statement remains open, being the first unknown case of the Chowla conjecture.)
has logarithmic density 1/4 was only established in 2015, but the natural density statement remains open, being the first unknown case of the Chowla conjecture.)
26 January, 2020 at 12:18 pm
Jeff
There are infinite sets where the natural and log densities are equivalent. But there are also, if I recall, infinite subsets where the natural density is not defined. And also infinite subsets where the natural density is zero. Bridging the gap between the two densities in light of all these obstacles seems crazy to me.
27 January, 2020 at 4:58 am
Jeff
Maybe you used this Theorem already,
Davenport–Erdős theorem.
The reverse direction iterations make the mind swirl. Trying to use the forms one gets to say whether some notion of logarithmic density transfers to natural density looks crazy.
My work gives concrete examples one can use to test the idea with. But even staying abstract is a waste of time.
I support horizontal progress, but it isn’t partial progress to me.
27 January, 2020 at 6:11 am
Jeff
Somewhere in the above arguments I saw n sub j minus n sub j, which is zero. Too tedious to track and check whether you’ve some indexing error. These iterations are a hell.
27 January, 2020 at 7:01 am
Jeff
Saw an inequality where it should perhaps read n sub (j -1) – 1 instead of n sub (j) – 1.
Anyway, epsilon cannot be between 0 and 1 and all of these inequalities hold in general.
26 January, 2020 at 6:07 am
Dmitriy Z
It seems that the inequality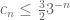 should be in other direction. So this implies that
should be in other direction. So this implies that 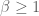 while an upper bound on
while an upper bound on 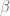 is
is  .
.
[Corrected, thanks – T.]
26 January, 2020 at 8:00 am
Jeff
I don’t think it is possible to find and ‘repair’ where all of the probabilistic type approaches “fail”. They fail from the start, and so cannot be ‘repaired”. There is no remedy. But it obviously won’t stop more folks from trying. Absolutely bizarre….
17 February, 2020 at 2:02 pm
Gottfried H
@Jeff – might you please provide a link to your work?
27 January, 2020 at 6:42 am
Anonymous
In the definition of , it seems that the constraint
, it seems that the constraint  should be removed.
should be removed.
[It’s actually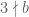 , but there was a LaTeX issue that I will try to correct – T.]
, but there was a LaTeX issue that I will try to correct – T.]
27 January, 2020 at 9:48 am
Anonymous
It seems simpler to just remove this constraint (thereby simplifying the expression for ) since this constraint (
) since this constraint ( ) clearly does not contribute to the probability expression of
) clearly does not contribute to the probability expression of  .
.
27 January, 2020 at 10:16 am
Terence Tao
Unfortunately this would then make the infimum equal to zero.
27 January, 2020 at 10:57 am
Anonymous
I meant that in the expression for , the probability in the RHS (for each fixed n) as a function of
, the probability in the RHS (for each fixed n) as a function of 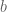 should vanish(!) whenever
should vanish(!) whenever  . Hence inclusion or removal of this constraint should not affect the expression for
. Hence inclusion or removal of this constraint should not affect the expression for  .
.
27 January, 2020 at 2:48 pm
Terence Tao
The infimum of a set of non-negative numbers will vanish if one or more zeroes are added to the set on which the infimum is taken. (This is in contrast to the supremum, which remains unaffected by addition of zero entries.)
27 January, 2020 at 7:51 am
David Speyer
In the definition of (just above equation (4)), should
(just above equation (4)), should 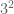 be
be 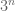 ?
?
[Corrected, thanks – T.]
27 January, 2020 at 8:11 am
David Speyer
Also, this isn’t an error, but it took me a while to figure out why the summand in Definition 1 is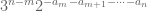 , but the summand in the 3-adic discussion below is
, but the summand in the 3-adic discussion below is 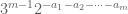 . (Answer: You made the change of variable
. (Answer: You made the change of variable  and reindexed
and reindexed  . So
. So  and
and  . Then you sent
. Then you sent 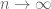 .)
.)
[Clarification added – T.]
27 January, 2020 at 8:20 am
Jürgen Sander
Dear Terence,
just for historical completeness you may wish to know that, independently of the work of Krasikov, a comparable â though slightly weaker (my constant 3/10, Krasikovâs constant 3/7) â result was published (see attachment) at the same time.
Best wishes,
Jürgen
“”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””
Prof. Dr. Jürgen Sander
Vizepräsident für Studium, Lehre, studentische Belange
und Digitalisierung
Universität Hildesheim
Universitätsplatz 1, D-31141 Hildesheim, Germany
Telefon.: +49 (0)5121 883-40140
Email: sander@imai.uni-hildesheim.de,
Sekret.: Tel. +49 (0)5121 883-40100, Fax +49 (0)5121 883-40101
“”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””
[Reference added – T.]
27 January, 2020 at 10:29 am
Allan van Hulst
I’m curious if you were able to resolve (some) of the difficulties described in the previous post relating to the explicit computation (where a technical limitation around n=10 arose, if I remember correctly).
29 January, 2020 at 4:03 am
Anonymous
Dear Pro.Tao,
By the way, firstly I would like to greet” Happy New Year” to you. Next, I need to suggest some ideas which is not related to above topic. I really think you do not spend most of time solving Collatz conjecture 100%. Your past Collatz conjecture paper was very good.If there is a string between Collatz, Goldbach, Twin prime, Riemann , you should do Collatz 100% as you as possible. My idea is very stupid , foolish and crazy. I do not need any one understands me.
I think you should spend most of time focusing on Hodge conjecture and Birch Swinnerton Dyer conjecture . I think two above problems are very easy if comparing the rest of 4 problems. The level of two problems is equal to Poincare conjecture. Poincare conjecture is very very very hard , but it there is still a point end “bottom”. In contrast of four rest problems, they do not have bottom like the center of Pacific ocean. I guarantee more 200 years ,noone can solve them.Although I am not an expert in maths, I believe in my sense completely. This is not proved by sience. I always use my sense to help and save many people. My predictions are always true and right in every field of human beings. I always want to bring many good things to you. Pro.Tao , you should quickly do the greatest thing before 50 age. Not over 65 age.
Today, a crazy man meets a genius man each other. I do not need you reply my question. I only want you think deeply my idea every night before bedtime. I always side by side to you.
Byebye ,Pro.Tao.
27 January, 2020 at 11:57 am
Ehud Schreiber
I seem to be confused – you say that c_3 and c_4 should be computed, but in the previous post it seems you’ve computed the steady-state distribution up to n=10, so essentially have the c’s up to that. If so, how does the “empirical” slope of -log_3(c_n) look like? Does it support beta = 1?
[I have that data on my home computer; will look it up later this afternoon -T.]
27 January, 2020 at 4:29 pm
Terence Tao
OK, here is the data I have:
2 0.031746 3.140
3 0.006096 2.321
4 0.001789 1.919
5 0.000445 1.756
6 0.000124 1.637
7 0.000035 1.555
8 0.000011 1.4785
9 0.000003 1.4331
10 0.000001 1.3941
(Not completely confident in the numerical accuracy of the n=10 data.)
Particularly reassuring is the fact that begins decreasing by a factor of close to 3 after a while, which is consistent with the upper bounds for
begins decreasing by a factor of close to 3 after a while, which is consistent with the upper bounds for 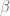 converging to 1. On the other hand it doesn’t look like brute force by itself is going to lead to any computationally feasible improvement of the Krasikov-Lagarias exponent this way.
converging to 1. On the other hand it doesn’t look like brute force by itself is going to lead to any computationally feasible improvement of the Krasikov-Lagarias exponent this way.
27 January, 2020 at 6:10 pm
Anonymous
Is it possible to combine the current approach with the Krasikov-Lagarias approach ?
28 January, 2020 at 10:38 am
Terence Tao
Good question! I think their linear programming approach could conceivably lead to some more refined bounds on that could lead to slightly sharper numerical upper bounds on
that could lead to slightly sharper numerical upper bounds on 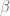 , and perhaps they may shed some light on how one might hope to reach
, and perhaps they may shed some light on how one might hope to reach  . Roughly speaking, translated to this setting, the approach proceeds by exploiting various inequalities between the more general quantities
. Roughly speaking, translated to this setting, the approach proceeds by exploiting various inequalities between the more general quantities
for various residue classes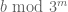 with
with  , thus for instance
, thus for instance  (and
(and  vanishes when
vanishes when 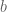 is a multiple of 3). Clearly these quantities are all non-negative with
is a multiple of 3). Clearly these quantities are all non-negative with
and there is also a recursive inequality
that follows easily from Lemma 1.12 of my paper. Thus for instance
etc.. One can then hope to prove various lower bounds of the form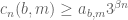 for various constants
for various constants  by induction provided that
by induction provided that  obey certain inequalities of their own (basically a dual set of inequalities to the ones listed above). This approach can probably improve slightly upon the bound
obey certain inequalities of their own (basically a dual set of inequalities to the ones listed above). This approach can probably improve slightly upon the bound 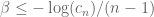 that I am using here (for instance I would imagine that the inequalities listed above would already improve upon the first bound
that I am using here (for instance I would imagine that the inequalities listed above would already improve upon the first bound  by a fair amount), though it would require significantly more numerical effort for any given value of
by a fair amount), though it would require significantly more numerical effort for any given value of  .
.
28 January, 2020 at 11:41 am
Terence Tao
Looking at the Krasikov-Lagarias paper, they observe a symmetry that I had not previously noticed, which in my notation is that
whenever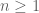 and
and 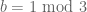 , which basically follows from splitting the geometric random variable
, which basically follows from splitting the geometric random variable  appearing in (2) as
appearing in (2) as  where
where 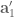 is another geometric random variable of mean 4/3 (so
is another geometric random variable of mean 4/3 (so  with probability
with probability  ) and
) and 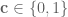 is a Bernoulli random variable of mean 2/3, independent of all the other variables, and then observing that the residue class of (2) mod 3 is entirely determined by
is a Bernoulli random variable of mean 2/3, independent of all the other variables, and then observing that the residue class of (2) mod 3 is entirely determined by  . So this simplifies the preceding calculations because we now have
. So this simplifies the preceding calculations because we now have  whenever
whenever 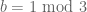 . In particular
. In particular  ,
,  , and the above system of inequalities basically simplifies after some calculation to
, and the above system of inequalities basically simplifies after some calculation to
leading to the bound instead of
instead of  . More generally I think with this new observation that the bound
. More generally I think with this new observation that the bound 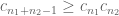 improves to
improves to 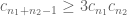 (we gain a factor of 3 in (5) now), leading to the improved bound
(we gain a factor of 3 in (5) now), leading to the improved bound  which for instance improves the
which for instance improves the 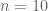 bound to
bound to 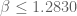 .
.
29 January, 2020 at 10:07 am
Anonymous
Is it possible that there are other similar splittings of random variables which may lead to additional other symmetries and recursive relations for more efficient computation of and improved related inequalities ?
and improved related inequalities ?
29 January, 2020 at 7:38 pm
Terence Tao
So I now realise that the above identity generalises to
for any integer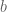 and any
and any 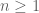 , with the convention that the second term on the RHS vanishes when
, with the convention that the second term on the RHS vanishes when 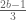 is not an integer. In fact this identity uniquely determines the Syracuse random variables. The identity follows from the fact that the geometric random variable
is not an integer. In fact this identity uniquely determines the Syracuse random variables. The identity follows from the fact that the geometric random variable  is equivalent to the random variable that equals
is equivalent to the random variable that equals 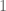 with probability
with probability 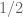 and
and 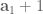 with probability
with probability 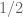 .
.
27 January, 2020 at 8:05 pm
Anonymous
Lemma 2 indicates the possible convexity of the sequence
 of (decreasing ?) upper bounds for
of (decreasing ?) upper bounds for 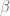 .
.
28 January, 2020 at 2:49 am
Ehud Schreiber
Writing a quick-and-dirty R code, I get the same results for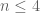 .
.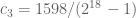 , so the cancellation persists. I can’t say for
, so the cancellation persists. I can’t say for 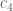 , as it involves
, as it involves  while double precision gives only 53 bits of precision…
while double precision gives only 53 bits of precision…
In particular,
Looking at the values of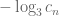 it certainly seems that
it certainly seems that 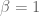 , although it would be difficult to distinguish between that and
, although it would be difficult to distinguish between that and  . It even seems that
. It even seems that 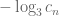 is
is  or even
or even  , but again distinguishing between that and
, but again distinguishing between that and  is impossible with this “empirical” data.
is impossible with this “empirical” data.
28 January, 2020 at 4:29 am
Jeff
You can you use my work to get real data to compare this bizarre guesswork with. It was a hell to figure out.
But unfavorable comparisons take all the fun out of guessing games. Better to keep the blinders on :).
28 January, 2020 at 8:56 am
Anonymous
This observed cancellation indicates that the sequence
 is a sequence of integers.
is a sequence of integers. can be used to find the corresponding recursive expression for
can be used to find the corresponding recursive expression for  which may be used to prove that
which may be used to prove that  is indeed a sequence of integers.
is indeed a sequence of integers.
If so, the recursive expression for
29 January, 2020 at 3:19 pm
Terence Tao
Numerically, I can obtain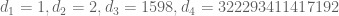 , and then I run out of precision. This sequence does not appear in the OEIS (of course, we haven’t yet proven that it is even a sequence of integers; perhaps if we do I will submit it there). But it is clear that the series grows extremely fast (one has
, and then I run out of precision. This sequence does not appear in the OEIS (of course, we haven’t yet proven that it is even a sequence of integers; perhaps if we do I will submit it there). But it is clear that the series grows extremely fast (one has  for instance).
for instance).
29 January, 2020 at 6:10 pm
Jeff
Yeah, I had to resort to doing the large calculations in my mind when my machine ran out of precision :). And of course my subsequent proofs are rigorous. But who cares?
28 January, 2020 at 10:19 am
Terence Tao
Interesting! I will check my own data later today but perhaps it can be conjectured that the probability densities are always integer multiples of
are always integer multiples of  . If this conjecture is true, it is presumably due to some alternate formula for these densities that I’m not seeing currently, but which may be worthwhile to uncover.
. If this conjecture is true, it is presumably due to some alternate formula for these densities that I’m not seeing currently, but which may be worthwhile to uncover.
29 January, 2020 at 9:56 am
Anonymous
This conjecture means that the cancelled factor is
28 January, 2020 at 3:59 am
J.P. McCarthy
that for all
for all 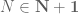 .
.
Should be .
.
[Corrected, thanks – T.]
29 January, 2020 at 1:30 am
Bogdan
You write:”…a positive density set of natural numbers iterates to an (explicitly computable) bounded set, so in principle the case \gamma=1 of (1) could now be verified by an (enormous) finite computation”
I do not understand this for two reasons.
First, the title of your paper talks about “almost bounded values”, not bounded ones. And to reduce the problem to finite computation, we ready need the orbits to iterate to BOUNDED set, not almost bounded one.
Second, the case \gamma=1 of (1) seems to correspond to “almost all” with NATURAL density, while your paper proves the statement for a different density.
Can you please clarify?
29 January, 2020 at 4:33 am
Jeff
I’m confused about why anyone would do the above bizarre guesswork when I already rid us of such crutches several years ago.
The quest for a positive density is a waste of time too, using probabilistic methods. Good grief people. Didn’t the 3x-1 case teach you all anything?
29 January, 2020 at 8:36 am
Terence Tao
This is discussed further in Remarks 1.4 and 3.1 of the paper. The argument that shows that almost all values iterate to almost bounded values also shows (and is in fact equivalent to) the assertion that for any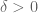 , there is a
, there is a 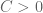 such that a set of natural numbers of logarithmic density at least
such that a set of natural numbers of logarithmic density at least 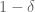 iterate to a value bounded by
iterate to a value bounded by  (and in fact the arguments give an in principle explicit relation between
(and in fact the arguments give an in principle explicit relation between  and
and 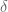 , which I believe to be of the form
, which I believe to be of the form 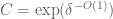 ). In particular, setting
). In particular, setting 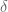 to be any fixed value between 0 and 1, e.g.,
to be any fixed value between 0 and 1, e.g.,  , we conclude that there is a positive (logarithmic) density set of numbers that iterates to an explicitly computable bounded set.
, we conclude that there is a positive (logarithmic) density set of numbers that iterates to an explicitly computable bounded set.
30 January, 2020 at 10:49 am
Jeff
Have you tried working this argument out with pre-images of 3x-1 ?
What do you mean exactly by ‘in principle’?
Is it explicit or not?
30 January, 2020 at 3:48 pm
Terence Tao
Every step in the argument can be made quantitative (with no ineffective bounds), so it is just a matter of carefully keeping track of all the implied constants if one wants. However, this would be time consuming and quite messy to optimize; usually it is more efficient to wait until the non-explicit form of an argument has become more streamlined before attempting to invest the effort to convert it to a fully explicit form.
Regarding the 3x-1 problem: it needs to be checked, of course, but I expect that pretty much all the results in my paper (or in this blog post) will carry over with only minor changes to the 3x-1 problem. Now it is of course true that the direct analogue of the Collatz conjecture is false for the 3x-1 conjecture due to the existence of the two known additional cycles (5,14,7,20,10) and (17,50, …, 34). However this does not exclude the possibility that progress can be made simultaneously on understanding both iterations. For instance, one could envisage that there is an argument common to both the 3x+1 and 3x-1 iterations that establishes the existence of an absolute constant C such that all orbits of either iteration end up reaching a number less than or equal to C: note that the two additional cycles of the 3x-1 iteration are not in contradiction to the above claim. If we could prove this partial result, and if C could be given explicitly and was of a computationally feasible magnitude, one could then finish off the 3x+1 conjecture for good by numerically verifying that all iterates of the 3x+1 map starting from a number less than or equal to C eventually reached 1. This would of course not work for the (false) 3x-1 conjecture due to the existence of the additional two cycles, so the failure of the 3x-1 conjecture does not prohibit this strategy from being a viable approach to the 3x+1 problem. [Basically, one should make a distinction between the asymptotic and non-asymptotic components of the dynamics. The 3x+1 and 3x-1 dynamics differ non-asymptotically (by which I mean the dynamics on small integers ) due to the additional cycles possessed by the former but not the latter, but there is no evidence at present that the asymptotic dynamics of the two (by which I mean the dynamics on large integers
) due to the additional cycles possessed by the former but not the latter, but there is no evidence at present that the asymptotic dynamics of the two (by which I mean the dynamics on large integers  ) are particularly different from each other. Indeed, one could unify the 3x+1 and 3x-1 dynamics by working on the integers rather than the natural numbers, in which case the unified conjecture asserts that all orbits eventually reach one of the five known cycles (listed for instance on the Wikipedia page), of which only one lives in the positive integers, with three others living in the negative integers and one being the zero cycle.]
) are particularly different from each other. Indeed, one could unify the 3x+1 and 3x-1 dynamics by working on the integers rather than the natural numbers, in which case the unified conjecture asserts that all orbits eventually reach one of the five known cycles (listed for instance on the Wikipedia page), of which only one lives in the positive integers, with three others living in the negative integers and one being the zero cycle.]
That said, I don’t view the results of my paper as coming close to giving a partial result of the above form. However, a realistic goal would be that of obtaining an explicit C for which iterations of either the 3x+1 or 3x-1 map would end up reaching a value C or below for a set of positive (logarithmic) density. Again, combined with a suitable numerical verification, this would establish the 3x+1 conjecture for a set of inputs of positive logarithmic density, without being in contradiction to the failure of the 3x-1 conjecture.
30 January, 2020 at 4:23 pm
Anonymous
It seems that establishing explicit numerical bounds corresponding to some given logarithmic densities and improving the current bound for
corresponding to some given logarithmic densities and improving the current bound for 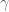 are suitable for a Polymath project.
are suitable for a Polymath project.
30 January, 2020 at 5:11 pm
Jeff
I must say I admire your optimism and energy. And I especially admire your dedication to your convictions. If you polymath this, doing large calculations on 3x-1 prior may help. Perhaps the ‘17’ cycle acts as a catch or net of sorts such that ‘more’, in the sense of some density measure, numbers map to it than the other two separately, whether or not there are more cycles.
Just stay healthy sir.
29 January, 2020 at 7:29 pm
Terence Tao
I can now establish that is always an integer multiple of
is always an integer multiple of  . In fact, if for any integer
. In fact, if for any integer 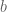 we define the quantities
we define the quantities
then one can show inductively that the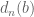 are all natural numbers.
are all natural numbers.
It is convenient to define for
for 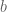 non-integer. Then
non-integer. Then  is periodic with period
is periodic with period 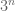 , and
, and  . This establishes the
. This establishes the 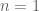 case. To obtain the higher
case. To obtain the higher  case we obtain a recursive formula for
case we obtain a recursive formula for 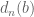 that only involves integer arithmetic. We can assume that
that only involves integer arithmetic. We can assume that 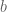 is an integer not divisible by 3, since
is an integer not divisible by 3, since 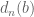 vanishes otherwise. From Lemma 1.12 of my paper and some calculation we see that
vanishes otherwise. From Lemma 1.12 of my paper and some calculation we see that
The main problem here is the denominator , which needs to be canceled. The key point here is that
, which needs to be canceled. The key point here is that
which is easily established by induction. Splitting the sum into triples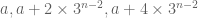 for
for  , we arrive at
, we arrive at
Now one observes that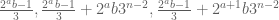 sweep out the residue classes mod
sweep out the residue classes mod  that reduce to
that reduce to  modulo
modulo 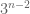 , hence
, hence
Using this and the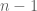 case of (1), we arrive after some calculation at the recursive identity
case of (1), we arrive after some calculation at the recursive identity
and hence the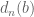 are all natural numbers.
are all natural numbers.
30 January, 2020 at 4:35 am
Jeff
A bit of Basic algebra works wonders. Well, now you have a small taste of the amount of work I did.
Getting hooked on this will wear you down. It’s not worth it.
30 January, 2020 at 10:01 am
Gabe Khan
I realize this might be too optimistic, and apologies again if this is obvious. However, from the recursive identity it seems that the most important term to get lower bounds on is
is  . Everything else in the series seems to be much smaller (i.e. grows slower than
. Everything else in the series seems to be much smaller (i.e. grows slower than  ). As such, if you could get an upper bound on how many small values of
). As such, if you could get an upper bound on how many small values of  you can pick so that
you can pick so that 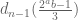 is zero (i.e. how many
is zero (i.e. how many  so that
so that  is divisible by 9), one might hope that this gives something to induct on to get lower bounds on the
is divisible by 9), one might hope that this gives something to induct on to get lower bounds on the  .
.
This alone is almost certainly not sharp enough to actually get good bounds, but that partial sum seems to be the key terms in the recursive formula.
30 January, 2020 at 3:35 pm
Terence Tao
Yes, this is the main term, and in fact the series should decay exponentially in , so that only the first few terms should be significant. It may indeed make sense to truncate the recursive formulae for these sorts of expressions to the low values of
, so that only the first few terms should be significant. It may indeed make sense to truncate the recursive formulae for these sorts of expressions to the low values of  (e.g.,
(e.g., 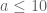 ) to obtain a sparser system of linear inequalities that could be more tractable even at the cost of a small amount of optimality in the final exponents.
) to obtain a sparser system of linear inequalities that could be more tractable even at the cost of a small amount of optimality in the final exponents.
31 January, 2020 at 8:32 am
Gabe Khan
Right, and since , this suggests that for a given
, this suggests that for a given  , we can expect to find
, we can expect to find 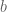 so that
so that  vanishes for
vanishes for 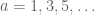 However, it seems like this is somehow the “worst case”. By truncating the series, the hope would be to verify this to some level. As you mentioned, there will definitely be some loss in this approximation.
However, it seems like this is somehow the “worst case”. By truncating the series, the hope would be to verify this to some level. As you mentioned, there will definitely be some loss in this approximation.
30 January, 2020 at 12:50 pm
Anonymous
A classical approach to estimate is to find from its recursive expression the corresponding (functional) identity satisfied by its generating function (e.g.
is to find from its recursive expression the corresponding (functional) identity satisfied by its generating function (e.g. 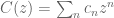 ) and estimate its coefficients (as done e.g. by the circle method for the partition function.)
) and estimate its coefficients (as done e.g. by the circle method for the partition function.)
30 January, 2020 at 3:37 pm
Terence Tao
This is indeed tempting; however the formulae for contain a minimum at one point, which does not interact well with classical generating functions. (There is a remote possibility that some sort of “tropical generating function” might be useful here, although those are more suited for working with maxima rather than minima.)
contain a minimum at one point, which does not interact well with classical generating functions. (There is a remote possibility that some sort of “tropical generating function” might be useful here, although those are more suited for working with maxima rather than minima.)
2 February, 2020 at 5:04 am
Dyachenko Eduard
In the table, the transformation introduced by Collaz for the number 27 is parsed.
The main proffer is reduced the “length of the number” when converting oddness of the form 4k+1and possibilities preserving it when converting 4k+3.
Since the transformation 4k+3 cannot be stored indefinitely, periodically the “length of the number” decreases.
As a result the sequence to transformed a number of the form 2^p/3^q
The work can be read here(https://zenodo.org/record/3630682#.XjagkGhKjIU).
i n(i) D(i) r(i)-r(i)>1 4k(i)+1 4k(i)+3 k(i) P(i)
0 27 1/ 2 -1 4*6+3 14+13 even 1
1 41 1/ 4 -2 2 4*10 + 1
2 31 1/ 2 -1 4*7+3 16+15 odd 4
3 47 1/ 2 -1 4*11+3 odd
4 71 1/ 2 -1 4*17+3 odd
5 107 1/ 2 -1 4*26+3 even
6 161 1/ 4 -2 2 4*40+1
7 121 1/ 4 -2 2 4*30+1
8 91 1/ 2 -1 4*22+3 46+45 even 1
9 137 1/ 4 -2 2 4*34+1
10 103 1/ 2 -1 4*25+3 52+51 odd 2
11 155 1/ 2 -1 4*38+3 even
12 233 1/ 4 -2 2 4*58+1
13 175 1/ 2 -1 4*43+3 88+87 odd 3
14 263 1/ 2 -1 4*65+3 odd
15 395 1/ 2 -1 4*98+3 even
16 593 1/ 4 -2 2 4*148+1
17 445 1/ 8 -3 3 4*111+1
18 167 1/ 2 -1 4*41+3 84+83 odd 2
19 251 1/ 2 -1 4*62+3 even
20 377 1/ 4 -2 2 4*94+1
21 283 1/ 2 -1 4*70+3 213+212 even 1
22 425 1/ 4 -2 2 4*106+1
23 319 1/ 2 -1 4*79+3 160+159 odd 5
24 479 1/ 2 -1 4*119+3 odd
25 719 1/ 2 -1 4*179+3 odd
26 1079 1/ 2 -1 4*269+3 odd
27 1619 1/ 2 -1 4*404+3 even
28 2429 1/ 8 -3 3 4*607+1
29 911 1/ 2 -1 4*227+3 456+455 odd 3
30 1367 1/ 2 -1 4*341+3 odd
31 2051 1/ 2 -1 4*512+3 even
32 3077 1/16 -4 4 4*769+1
33 577 1/ 4 -2 2 4*144+1
34 433 1/ 4 -2 2 4*108+1
35 325 1/16 -4 4 4*81+1
36 61 1/ 8 -3 3 4*15+1
37 23 1/ 2 -1 4*5+3 12+11 odd 2
38 35 1/ 2 -1 4*8+3 even
39 53 1/32 -5 5 4*13+1
40 5 1/16 -4 4 4*1+1
41 1 1/ 1 0
balance -70 46 24
Text is available under the Creative Commons NonCommercial-NoDerivatives 4.0 International
(CC BY-NC-ND 4.0)
2 February, 2020 at 5:50 am
Dyachenko Eduard
Unfortunately, the table is not obvious, although I tried to insert correctly.
The work can be read here(https://zenodo.org/record/3630682#.XjagkGhKjIU).
7 February, 2020 at 6:48 am
y.y.
apologies for my english.
I have commented your previous blog posts about the conjecture. there I have appended professor Peter Hellekalek’s this paper:
https://arxiv.org/abs/1605.02634
the paper seems to concern Syracuse function in 3-adic as you mentioned.
and I wrote that ∀x∈(2N_0+1), ∃μ∈N, f^(1+μ)(x)<x.
because the function have its inverse and it can be defined by RCWA with metrices.
the structure contains S_3 especially C_3 and yes, 2-adic is somehow combined. there is no randomness.
I don’t have background in mathematics, but I would be grateful if professor Tao could get to know my findings. it seems something important to prove (or progress to prove) the conjecture. thank you.
8 February, 2020 at 2:35 am
y.y.
Mistake. when x=1, f^(1+μ)(x)=x. 1 is a unique fixed-point. and μ=2, of course. As for the indices μ, it can also be defined as resides when it is in inverse form.
10 February, 2020 at 7:33 pm
y.y.
So the particular orbit such as; x∈2N_0+1, Syrac(x)→2N_0+1:= (3x+1)/2^-(1+n), Syrac(x)>x.
These numbers can be determined as certain subset. Looking at the subset as in inverse, we can also demermine the image of the subset. Then consider the intersection of the image and its preimage, we see that the set of the intersecion goes to null at m times. I think that is not so interesting part of the problem for mathematicians. The interesting obserbation of the problem is that the syracuse function has its inverse which S_3 acts on.
10 February, 2020 at 8:46 pm
Anonymous
Again mistake. Remove “/” or “-” from (3x+1)/2^-(1+n) ! Don’t factorial!
10 February, 2020 at 9:14 am
Peter C
I’ve worked on this problem with varying approaches over the years. Recently msg’d you via email on a traverse method to the 3x+1 tree. Sourcing from odd multiple of 3 numbers, the problem can be converted into an infinite density series to explain that all numbers land at key nodes N*, and vice versa. Those key nodes (N*) all descend in a formulated way (which another infinite density series can explain) to other N*. I’d love to chat with you about it.
18 February, 2020 at 10:16 am
Peter C
As mentioned previously, if one defines a way to progress outward rather than the typical inward motions (i.e. to land a 1) it is easily shown that all numbers flow outwards to Mod(n,3)=0 nodes; traversing in the odd numbers only.
Such a step can be declared as:
NewN = w [(-3*(w^2)+7w)n -1] / [3(2^(w-1))], where w=MOD(n,3)
E.g 5->3, w=2, n=5, NewN=3; This would count as 1 step to get to divisible by 3.
A number like 17 would require 3 steps to get to a divisible by 3 outer node, div3 require no steps (i.e. 3, 9, 21, etc.)
This approach yields a density series: (x:0 to inf) Ʃ [2^x] / [3^(x+1)] = 1,
where x = STEPS to get w=0
However, such a method doesn’t guarantee that a given number & chain actually attaches to the rest of tree. Therefore a secondary density series explains that the attaching nodes all derive from other attaching nodes.
So Logically, if all numbers flow outwards to a div3, that chain contains an N* (can be considered the source node for that chain of nodes), N* comes from a (N*-1)/4 node [which will flow inward to its own relative N* and outward div3], etc.. A similar series can be generated here to ensure the total sum =1 as well.
Example: 35 would have 2 steps to to get to a div3. Its N* is 53, (N*-1)/4 = 13, 13 is an N*,
(13-1)/4 = 3, its N* is 5 (the base case).
This would account for all chains, unless one odd number out there isn’t part of a chain. If that happens, it would seem contradictory because that means an infinite amount of chains & nodes exist (so far not seen) that don’t link back using the (N*-1)/4 rule.
It my impression that the typical approaches to solving this problem are the problem.
26 February, 2020 at 7:43 am
Anonymous
The main proffer is reduced the “length of the number” when converting oddness of the form 4k+1and possibilities preserving it when converting 4k+3.
Since the transformation 4k+3 cannot be stored indefinitely, periodically the “length of the number” decreases.
26 February, 2020 at 7:59 am
Peter C
I believe you are saying the method I have suggested gives a way to convert the overall tree into odds from {4K+1,4K+3} forms. Yes. The important aspect is the periodic nature of the Steps. Using densities to understand the entire set of odd numbers, you can convert the tree into the series mentioned above (x:0 to inf) Ʃ [2^x] / [3^(x+1)] = 1. The secondary part of most importance is only one N* exists in a chain, and that is joins to another N* as well. One must decompose the tree in a slightly different manner that it is typical known, but is equivalent… the answer becomes apparent then. All number flow outwards to a multiple of 3, all multiple of 3 have exactly 1 N* in its chain, and N* join inwards. Each have density series that are cyclical and sum to 1.
18 February, 2020 at 12:24 am
y.y.
I am really glad if the conjecture would be affirmatively solved in the near future because I’ve been obsessed this. I have no mathematical background nor related areas so that I cannot write the paper about this in my own. but again say, I have found the inverse map of the Syracuse map which is known as a surjective but not injective mapping. The inverse map has of course one-one correspondence for all x∈2N_0+1. The conjecture is for group theory. I wonder who should I contact to discuss this.
18 February, 2020 at 11:33 am
Anonymous
Alex Kontorovich’s twitter thread is really interesting, another thing to keep us up at night. I guess it isn’t lost on you that it’s reminiscent of your approach to Navier-Stokes blowup.
18 February, 2020 at 12:05 pm
Anonymous
Another (graph theoretic) interpretation of the Collatz conjecture is that it is equivalent to the connectedness of the (infinite) graph corresponding to the Col mapping and that this graph has only the trivial cycle.
Is it possible that graph theoretic methods may help to get more results ?
16 March, 2020 at 8:55 pm
Arunava mondal
Very good explanation.
16 March, 2020 at 8:56 pm
Arunava mondal
Sir what is formality conjecture.
12 August, 2020 at 8:41 pm
Li Jiang
The essence of Collatz conjecture is the iterative operation of odd numbers. It is known from the basic theorem of arithmetic: the number of factors with a value equal to 2 in each even number is determined for the even number, so an iterative operation for odd numbers can be defined:
can be defined: 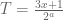 , (where
, (where  is the number of factors whose value in
is the number of factors whose value in 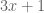 is equal to 2), the result of the operation
is equal to 2), the result of the operation 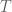 is still odd number. According to this definition, the general formula for continuous iteration of odd number can be derived
is still odd number. According to this definition, the general formula for continuous iteration of odd number can be derived
From this, if the continuous iteration may cause loops, then we can deduce the equation
Solving this equation can get the result that the equation has no positive integer solution except 1, which indicates that continuous iteration cannot cause a loop.
On the other hand, the continuous iterative formula can be transformed into a linear indefinite equation
The process of solving the equation reveals that it is impossible for odd numbers to reach infinity through iterative operations. Therefore, all odd numbers will return to 1 after a limited number of iterations.
By extending this result to even numbers, it can be determined that all positive integers will return to 1 after a finite number of iterations, which fully proves Collatz conjecture.
My article The Collatz conjecture and linear indefinite equation is in the following website
http://www.sciepub.com/tjant/content/8/2
12 August, 2020 at 11:01 pm
Anonymous
where is the 0.8 in your equation 4.9 coming from?
13 August, 2020 at 2:01 am
Li Jiang
13 August, 2020 at 4:27 am
Li Jiang
Correction: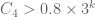
13 August, 2020 at 11:49 am
Anonymous
You mean ?
? 
13 August, 2020 at 11:51 am
Anonymous
13 August, 2020 at 3:35 pm
Hollis Williams
13 August, 2020 at 1:57 pm
Li Jiang
Sorry, it should the sum of the first 4 items of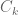 be greater than
be greater than 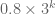 .
.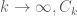 is divergent, but
is divergent, but  is always a finite value.
is always a finite value.
When
13 August, 2020 at 11:06 pm
Anonymous
$A_k = 2^{g(k)}$ where $g(k)$ is typically less than $k$. So $\frac{C_k}{A_k}\approx\frac{3^k}{2^k}$ which also diverges.
14 August, 2020 at 2:34 am
Li Jiang
Please read my article: and
and  of the indefinite equation, formula (4.8) is obtained, where
of the indefinite equation, formula (4.8) is obtained, where

In the process of determining the special solutions
Since $latex r_2 \frac{C_k}{A_k}+u.$
Therefore, if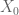 is finite then
is finite then  cannot be divergent.
cannot be divergent.
14 August, 2020 at 2:42 am
Anonymous
since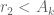
14 August, 2020 at 2:43 am
Anonymous
so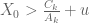
12 February, 2021 at 5:31 am
Cifra Finale
Dear prof. Tao and readers of this blog, we are Dr. Cinzia, Silvana graduate in Materials Technology and their Dad Giovanni Di Savino, Air Force technician, we believe that Collatz’s conjecture can be simplified: Euclid with the formula 2 * n + 1 generates infinite odd numbers and proves that there is a prime number greater than the largest known prime. Certainly the first known and the first greater than the first known can be generated and identifiable but no prime can be generated that can be defined as the first greater than all the former. Thales measures “the inaccessible and unattainable”, Euclid generates and demonstrates the existence of the inaccessible and unreachable prime number, Gauss with the Fundamental Theorem of Arithmetic demonstrates the factorization mentioned by Euclid and states that every natural number is the product of prime numbers. Einstein, with the theory of relativity and with E = m * c ^ 2 shows that as the digits that make up the number increase, (the largest prime number we know today we write it with the power notation of two minus one (2 ^ 82.589. 933 -1) or with 24,862,048 decimal digits that can be reported on paper in km of writing) the same becomes inaccessible and unreachable, the “space” to be analyzed increases and the quantity = space to be processed which can be communicated with a maximum speed that does not can exceed: “the speed of light”. Larger numbers correspond to larger spaces, it follows that it takes longer to process that number which, however large, inaccessible and unreachable it may be Euclid has shown that it exists, Thales has shown that it can be measured and Einstein made us take act and showed us that our life cycles are insufficient to know the prime number greater than the largest known. The natural numbers, also generated with primes that exist and that we will never know, are the even and odd numbers that can be in a sequence that must be considered in the Collatz conjecture. Results of verification of numbers already made, are to be considered as records to be overcome. The numbers and sequences referred to in the conjecture are infinite and therefore it is impossible to represent the sequences but it is possible to satisfy the conjecture,.Statement in 1930 by the German mathematician Lothar Collatz, the procedure is also known as the Ulam or Thwaites conjecture, as the Kakutani or Syracuse problem, as the Hasse algorithm, or even as the hail sequence. Intuition might suggest that the number you start with affects the number you end up with but Collatz predicted that if you start with a positive integer and run this process long enough, all initial values will lead to 1. And once you reach 1 , the rules of Collatz’s conjecture limit you to one cycle: 1, 4, 2, 1, 4, 2, 1, over and over forever. Euclid formulating 2 * n + 1 generates all the infinite odd numbers which, factored with the Fundamental Theorem of Arithmetic, do not have 2 among their factors; Collatz formulating n * 3 + 1 makes even any odd number of starting or sequence of the statement of Collatz; the even number or which has become even has 2 among its factors and any even number is a multiple of it. The result of an even number divided by 2 can also be an odd number but Collatz with its algorithm (n * 3 + 1) makes any known and unknown odd number even and the known and unknown even number can be divided by 2 and , halving the even numbers, we always arrive at 2/2 = 1 which being odd becomes 4 (1 * 3 + 1) which in turn becomes 2 (4/2) and then 2/2 = 1 to continue indefinitely 1_4_2 . thanks for reading
3 April, 2021 at 4:56 am
sacirisi
The Fundamental Theorem of Arithmetic proves that the infinite (hereinafter ∞) natural numbers are primes or compounds and are the producer of prime numbers; satisfying the two versions of Goldbach’s conjecture will allow us to prove that even ∞ natural numbers are the sum of 2 prime numbers, ∞ odd numbers are the sum of only 3 prime numbers; satisfying Euclid’s twin primes conjecture allows us to give a solution to the strong version of Goldbach’s conjecture, “all even ∞ are the sum of two primes” by not looking for the impossible combinatorics between two primes whose quantity and value we do not know , but analyzing the distances between two consecutive prime numbers spaced only by the multiple numbers. https://www.facebook.com/groups/5349868060/?multi_permalinks=10158013236403061
28 September, 2021 at 12:20 am
sacirisi
mutatis mutandis at 20210927. The Collatz conjecture is defined as a quagmire or labyrinth from which it is best to stay away. I went in, I left and I can go in and out whatever the starting number. The only way to get out of the “quagmire or labyrinth” was known that it was necessary to find the way to get to 1. All even numbers that are the result of a power of 2 arrive at 1, from half of the smaller power 2 ^ 1 to the middle from the largest and the smallest generable. The even number is: either a choice of the starting number and, if it is the result of 2 ^ n, we arrive at 1 after so many divisions by 2 equal to the value of the exponent of the power of 2, or it is the result of a number odd * 3 + 1. There is the odd number that multiplying it * 3 + 1 obtains a result equal to the result of a power of 2 with even exponent ≥2. The primes are infinite and are generated by the known primes, the odd numbers that * 3 + 1 generate the powers “to get out of the quagmire” are infinite and are the sum of the results of the even powers ≥0 notes or the odd binary number with digits which are the results of even powers ≥0. Each starting number generates new, unique and unrepeatable numbers; among these there is an odd number which is the sum of the results of powers of 2 with even exponent. https://www.facebook.com/photo/?fbid=3082225312098634&set=pcb.10158351014883061 Emzari Papava Fan Club
15 October, 2021 at 5:10 am
sacirisi
mutatis mutandis at 15 apr: Because the Collatz algorithm will never create an infinite loop. With any natural number and with the Collatz algorithm we obtain an odd number that multiplying it * 3 + 1 generates an even number which is the result of a power of 2, the algorithm halves even numbers, results of powers of 2 , until you get 1. All numbers end with a power of 2, all numbers end at 1. il lavoro:https://www.facebook.com/groups/5349868060
15 October, 2021 at 5:12 am
sacirisi
The steps to get to 1: will never know the factors of natural numbers which are the result of the production of prime numbers raised to a power equal to a natural number. We do not know which is the largest number to verify and we will never know the largest value of the exponent of the factor 2. In the Collatz conjecture, this value determines the steps required to halve an even number and arrive at an odd number. For an even number that is the result of a power of 2, the number of operations required to reach 1 is the exponent value of the power of 2; for an even number which is the result of the product of a power of 2 and powers of odd primes, the number of operations necessary to arrive at 1 is the sum of the exponents of all powers of 2 which are factors of the even numbers that the algorithm generates by multiplying the odd * 3 + 1 and that, with the power of the final 2, include the succession of values that the algorithm generates in each starting number.
6 May, 2021 at 5:21 am
Anonymous
I would like to share my result on the problem with polymath project.
I tried to write the result mathematically as possible as I could.
There might be some mistakes on notations because I am not a math-researcher, sorry.
I think this would be some of help for understanding that the pseudo-randomness, invariant measure, and the most difficulty part of the problem. Thank you.
https://drive.google.com/file/d/1KtzjqtceHlf5sCvjEMCkVvnVQbMo8nFP/view?usp=sharing
https://drive.google.com/file/d/1TmiKN4vLwY3r3gZ367u1G8hjrTNtFVr0/view?usp=sharing
22 August, 2021 at 2:29 am
Alberto Ibañez
On falling into a non-trivial orbit Dear professor, despite trying to understand your arguments, I can’t, but I still wanted to ask you if with this technique, using the pre-images, Collatz’s conjecture in reverse, it would be possible to show that every orbit has a multiple of three (actually every orbit originates from a multiple of 3)?
22 August, 2021 at 1:09 pm
Terence Tao
Yes, this is true. For if is not a multiple of
is not a multiple of  , then simple modular arithmetic reveals that
, then simple modular arithmetic reveals that  for some natural number
for some natural number  . Then
. Then 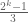 is a multiple of three whose orbit will contain
is a multiple of three whose orbit will contain  .
.
23 August, 2021 at 12:10 pm
Alberto Ibañez
Thank you Professor and excuse me because I think I am not expressing myself well.
Every n odd multiple of 3 (or an orbit containing one) cannot fall into a non-trivial periodic orbit
Is it proven that no odd n can fall into periodic orbit? I think not yet, right?
So I was wondering if your technique could be used to show that every reverse orbit contains an odd n multiple of 3 (the origin).
Orbits that escape to infinity
I take the opportunity to ask what is the value of the fact that, if k is the number of multiplications by 3 and y is the number of divisions by 2, when k goes to infinity, y-k also goes to infinity
This is deduced from an accelerated Col2 type map, which follows the worst possible trajectory, ascending, in the sense of the time an orbyt maintaining a multiplication by 3 and a division by 2, and ensures that for all odd n, its worst trajectory, in this sense, is finite, and ends up dividing more than once by 2
If n odd, n + 1 even = z * 2 ^ t, then in t steps of a Col2 map the worst orbit ends, in this sense
Thanks
30 October, 2022 at 7:13 am
sacirisi
With the Collatz algorithm it is not possible to process all natural numbers because we do not know: quantities and values of even and odd numbers and all their factors. From Tartaglia’s triangle we can detect odd numbers which are the sum of the results of the infinite powers of 2 which have an even index and which are also equal to the previous odd * 4 + 1. These are all the odd numbers that * 3 + 1 generate an even number that is the result of a base power 2 and even index 2 ^ (2 * n≥1) and that, the nth half, ends at 1 because ½ of 2 ^ 1 = 2 ^ 0 = 1. pre print https://vixra.org/abs/2112.0004
27 October, 2023 at 7:39 am
Cynthia Moore
ISO someone interested in reviewing my Collatz sketch. Please contact CynthiaMooreMath@gmail.com. Thanks!