One of the most well known problems from ancient Greek mathematics was that of trisecting an angle by straightedge and compass, which was eventually proven impossible in 1837 by Pierre Wantzel, using methods from Galois theory.
Formally, one can set up the problem as follows. Define a configuration to be a finite collection of points, lines, and circles in the Euclidean plane. Define a construction step to be one of the following operations to enlarge the collection
:
- (Straightedge) Given two distinct points
in
, form the line
that connects
and
, and add it to
.
- (Compass) Given two distinct points
in
, and given a third point
in
(which may or may not equal
or
), form the circle with centre
and radius equal to the length
of the line segment joining
and
, and add it to
.
- (Intersection) Given two distinct curves
in
(thus
is either a line or a circle in
, and similarly for
), select a point
that is common to both
and
(there are at most two such points), and add it to
.
We say that a point, line, or circle is constructible by straightedge and compass from a configuration if it can be obtained from
after applying a finite number of construction steps.
Problem 1 (Angle trisection) Let
be distinct points in the plane. Is it always possible to construct by straightedge and compass from
a line
through
that trisects the angle
, in the sense that the angle between
and
is one third of the angle of
?
Thanks to Wantzel’s result, the answer to this problem is known to be “no” in general; a generic angle cannot be trisected by straightedge and compass. (On the other hand, some special angles can certainly be trisected by straightedge and compass, such as a right angle. Also, one can certainly trisect generic angles using other methods than straightedge and compass; see the Wikipedia page on angle trisection for some examples of this.)
The impossibility of angle trisection stands in sharp contrast to the easy construction of angle bisection via straightedge and compass, which we briefly review as follows:
- Start with three points
.
- Form the circle
with centre
and radius
, and intersect it with the line
. Let
be the point in this intersection that lies on the same side of
as
. (
may well be equal to
).
- Form the circle
with centre
and radius
, and the circle
with centre
and radius
. Let
be the point of intersection of
and
that is not
.
- The line
will then bisect the angle
.
The key difference between angle trisection and angle bisection ultimately boils down to the following trivial number-theoretic fact:
Proof: Obvious by modular arithmetic, by induction, or by the fundamental theorem of arithmetic.
In contrast, there are of course plenty of powers of that are evenly divisible by
, and this is ultimately why angle bisection is easy while angle trisection is hard.
The standard way in which Lemma 2 is used to demonstrate the impossibility of angle trisection is via Galois theory. The implication is quite short if one knows this theory, but quite opaque otherwise. We briefly sketch the proof of this implication here, though we will not need it in the rest of the discussion. Firstly, Lemma 2 implies the following fact about field extensions.
Corollary 3 Let
be a field, and let
be an extension of
that can be constructed out of
by a finite sequence of quadratic extensions. Then
does not contain any cubic extensions
of
.
Proof: If contained a cubic extension
of
, then the dimension of
over
would be a multiple of three. On the other hand, if
is obtained from
by a tower of quadratic extensions, then the dimension of
over
is a power of two. The claim then follows from Lemma 2.
To conclude the proof, one then notes that any point, line, or circle that can be constructed from a configuration is definable in a field obtained from the coefficients of all the objects in
after taking a finite number of quadratic extensions, whereas a trisection of an angle
will generically only be definable in a cubic extension of the field generated by the coordinates of
.
The Galois theory method also allows one to obtain many other impossibility results of this type, most famously the Abel-Ruffini theorem on the insolvability of the quintic equation by radicals. For this reason (and also because of the many applications of Galois theory to number theory and other branches of mathematics), the Galois theory argument is the “right” way to prove the impossibility of angle trisection within the broader framework of modern mathematics. However, this argument has the drawback that it requires one to first understand Galois theory (or at least field theory), which is usually not presented until an advanced undergraduate algebra or number theory course, whilst the angle trisection problem requires only high-school level mathematics to formulate. Even if one is allowed to “cheat” and sweep several technicalities under the rug, one still needs to possess a fair amount of solid intuition about advanced algebra in order to appreciate the proof. (This was undoubtedly one reason why, even after Wantzel’s impossibility result was published, a large amount of effort was still expended by amateur mathematicians to try to trisect a general angle.)
In this post I would therefore like to present a different proof (or perhaps more accurately, a disguised version of the standard proof) of the impossibility of angle trisection by straightedge and compass, that avoids explicit mention of Galois theory (though it is never far beneath the surface). With “cheats”, the proof is actually quite simple and geometric (except for Lemma 2, which is still used at a crucial juncture), based on the basic geometric concept of monodromy; unfortunately, some technical work is needed however to remove these cheats.
To describe the intuitive idea of the proof, let us return to the angle bisection construction, that takes a triple of points as input and returns a bisecting line
as output. We iterate the construction to create a quadrisecting line
, via the following sequence of steps that extend the original bisection construction:
- Start with three points
.
- Form the circle
with centre
and radius
, and intersect it with the line
. Let
be the point in this intersection that lies on the same side of
as
. (
may well be equal to
).
- Form the circle
with centre
and radius
, and the circle
with centre
and radius
. Let
be the point of intersection of
and
that is not
.
- Let
be the point on the line
which lies on
, and is on the same side of
as
.
- Form the circle
with centre
and radius
. Let
be the point of intersection of
and
that is not
.
- The line
will then quadrisect the angle
.
Let us fix the points and
, but not
, and view
(as well as intermediate objects such as
,
,
,
,
,
,
) as a function of
.
Let us now do the following: we begin rotating counterclockwise around
, which drags around the other objects
,
,
,
,
,
,
that were constructed by
accordingly. For instance, here is an early stage of this rotation process, when the angle
has become obtuse:
Now for the slightly tricky bit. We are going to keep rotating beyond a half-rotation of
, so that
now becomes a reflex angle. At this point, a singularity occurs; the point
collides into
, and so there is an instant in which the line
is not well-defined. However, this turns out to be a removable singularity (and the easiest way to demonstrate this will be to tap the power of complex analysis, as complex numbers can easily route around such a singularity), and we can blast through it to the other side, giving a picture like this:
Note that we have now deviated from the original construction in that and
are no longer on the same side of
; we are thus now working in a continuation of that construction rather than with the construction itself. Nevertheless, we can still work with this continuation (much as, say, one works with analytic continuations of infinite series such as
beyond their original domain of definition).
We now keep rotating around
. Here,
is approaching a full rotation of
:
When reaches a full rotation, a different singularity occurs:
and
coincide. Nevertheless, this is also a removable singularity, and we blast through to beyond a full rotation:
And now is back where it started, as are
,
,
, and
… but the point
has moved, from one intersection point of
to the other. As a consequence,
,
, and
have also changed, with
being at right angles to where it was before. (In the jargon of modern mathematics, the quadrisection construction has a non-trivial monodromy.)
But nothing stops us from rotating some more. If we continue this procedure, we see that after two full rotations of
around
, all points, lines, and circles constructed from
have returned to their original positions. Because of this, we shall say that the quadrisection construction described above is periodic with period
.
Similarly, if one performs an octisection of the angle by bisecting the quadrisection, one can verify that this octisection is periodic with period
; it takes four full rotations of
around
before the configuration returns to where it started. More generally, one can show
Proposition 4 Any construction of straightedge and compass from the points
is periodic with period equal to a power of
.
The reason for this, ultimately, is because any two circles or lines will intersect each other in at most two points, and so at each step of a straightedge-and-compass construction there is an ambiguity of at most . Each rotation of
around
can potentially flip one of these points to the other, but then if one rotates again, the point returns to its original position, and then one can analyse the next point in the construction in the same fashion until one obtains the proposition.
But now consider a putative trisection operation, that starts with an arbitrary angle and somehow uses some sequence of straightedge and compass constructions to end up with a trisecting line
:
What is the period of this construction? If we continuously rotate around
, we observe that a full rotations of
only causes the trisecting line
to rotate by a third of a full rotation (i.e. by
):
Because of this, we see that the period of any construction that contains must be a multiple of
. But this contradicts Proposition 4 and Lemma 2.
Below the fold, I will make the above proof rigorous. Unfortunately, in doing so, I had to again leave the world of high-school mathematics, as one needs a little bit of algebraic geometry and complex analysis to resolve the issues with singularities that we saw in the above sketch. Still, I feel that at an intuitive level at least, this argument is more geometric and accessible than the Galois-theoretic argument (though anyone familiar with Galois theory will note that there is really not that much difference between the proofs, ultimately, as one has simply replaced the Galois group with a closely related monodromy group instead).
— 1. Details —
We now make the argument more rigorous. We will assume for sake of contradiction that for every triple of distinct points, we can find a construction by straightedge and compass that trisects the angle
, and eventually deduce a contradiction out of this.
We remark that we do not initially assume any uniformity in this construction; for instance, it could be possible that the trisection procedure for obtuse angles is completely different from that of acute angles, using a totally different set of constructions, while some exceptional angles (e.g. right angles or degenerate angles) might use yet another construction. We will address these issues later.
The first step is to get rid of some possible degeneracies in one’s construction. At present, nothing in our definition of a construction prevents us from adding a point, line, or circle to the construction that was already present in the existing collection of points, lines, and circles. However, it is clear that any such step in the construction is redundant, and can be omitted. Thus, we may assume without loss of generality that for each
, the construction used to trisect the angle contains no such redundant steps. (This may make the construction even less uniform than it was previously, but we will address this issue later.)
Another form of degeneracy that we will need to eliminate for technical reasons is that of tangency. At present, we allow in our construction the ability to take two tangent circles, or a circle and a tangent line, and add the tangent point to the collection (if it was not already present in the construction). This would ordinarily be a harmless thing to do, but it complicates our strategy of perturbing the configuration, so we now act to eliminate it. Suppose first that one had two circles already constructed in the configuration
and tangent to each other, and one wanted to add the tangent point
to the configuration. But note that in order to have added
and
to
, one must previously have added the centres
and
of these circles to
also. One can then add
to
by intersecting the line
with
and picking the point that lies on
; this way, one does not need to intersect two tangent curves together.
Similarly, suppose that we already had a circle and a tangent line
already constructed in the configuration, but with the tangent point
absent. The centre
of
, and at least two points
on
, must previously have also been constructed in order to have
and
present; note that
are not equal to
by hypothesis. One can then obtain
by dropping a perpendicular from
to
by the usual construction (i.e. drawing a circle centred at
with radius
to hit
again at
, then drawing circles from
and
with the same radius
to meet at a point
distinct from
, then intersecting
with
to obtain
), thus avoiding tangencies again. (This construction may happen to use lines or circles that had already appeared in the construction, but in those cases one can simply skip those steps.)
As a consequence of these reductions, we may now assume that our construction is nondegenerate in the sense that
- Any point, line, or circle added at a step in the construction, does not previously appear in that construction.
- Whenever one intersects two circles in a construction together to add another point to the construction, the circles are non-tangent (and thus meet in exactly two points).
- Whenever one intersects a circle and a line in a construction together to add another point to the construction, the circle and line are non-tangent (and thus meet in exactly two points).
The reason why we restrict attention to nondegenerate constructions is that they are stable with respect to perturbations. Note for instance that if one has two circles that intersect in two different points, and one of them is labeled
, then we may perturb
and
by a small amount, and still have an intersection point close to
(with the other intersection point far away from
). Thus,
is locally a continuous function of
and
. Similarly if one forms the intersection of a circle and a secant (a line which intersects non-tangentially). In a similar vein, given two points
and
that are distinct, the line between them
varies continuously with
and
as long as one does not move
and
so far that they collide; and given two lines
and
that intersect at a point
(and in particular are non-parallel), then
also depends continuously on
and
. Thus, in a nondegenerate construction starting from the original three points
, every point, line, or circle created by the construction can be viewed as a continuous function of
, as long as one only works in a sufficiently small neighbourhood of the original configuration
. In particular, the final line
varies continuously in this fashion. Note however that the trisection property may be lost by this perturbation; just because
happens to trisect
when
are in the original positions, this does not necessarily imply that after one perturbs
, that the resulting perturbed line
still trisects the angle. (For instance, there are a number of ways to trisect a right angle (e.g. by bisecting an angle of an equilateral triangle), but if one perturbs the angle to be slightly acute or slightly obtuse, the line created by this procedure would not be expected to continue to trisect that angle.)
The next step is to allow analytic geometry (and thence algebraic geometry) to enter the picture, by using Cartesian coordinates. We may identify the Euclidean plane with the analytic plane ; we may also normalise
to be the points
,
by this identification. We will also restrict
to lie on the unit circle
, so that there is now just one degree of freedom in the configuration
. One can describe a line in
by an equation of the form
(with not both zero), and describe a circle in
by an equation of the form
with non-zero. There is some non-uniqueness in these representations: for the line, one can multiply
by the same constant without altering the line, and for the circle, one can replace
by
. However, this will not be a serious concern for us. Note that any two distinct points
,
determine a line
and given three points ,
,
, one can form a circle
with centre and radius
. Given two distinct non-parallel lines
and
their unique intersection point is given as
similarly, given two circles
and
their points of intersection (if they exist in ) are given as
and
and the points of intersection between and
(if they exist in
) are given as
The precise expressions given above are not particularly important for our argument, save to note that these expressions are always algebraic functions of the input coordinates such as , defined over the reals
, and that the only algebraic operations needed here besides the arithmetic operations of addition, subtraction, multiplication, and division is the square root operation. Thus, we see that any particular construction of, say, a line
from a configuration
will locally be an algebraic function of
(recall that we have already fixed
), and this definition can be extended until one reaches a degeneracy (two points, lines, or circles collide, two curves become tangent, or two lines become parallel); however, this degeneracy only occurs in an proper real algebraic set of configurations, and in particular for
in a dimension zero subset of the circle
.
These degeneracies are annoying because they disconnect the circle , and can potentially block off large regions of that circle for which the construction is not even defined (because two circles stop intersecting, or a circle and line stop intersecting, in
, due to the lack of a real square root for negative numbers). To fix this, we move now from the real plane
to the complex plane
. Note that the algebraic definitions of a line and a circle continue to make perfect sense in
(with coefficients such as
now allowed to be complex numbers instead of real numbers), and the algebraic intersection formulae given previously continue to make sense in the complex setting. The point
now is allowed to range in the complex circle
, which is a Riemann surface (conformal to the Riemann sphere
after stereogrpahic projection). Furthermore, because all non-zero complex numbers have square roots, any given construction that was valid for at least one configuration is now valid (though possibly multi-valued) as an algebraic function on
outside of a dimension zero set of singularities, i.e. outside of a finite number of exceptional values of
. But note now that these singularities do not disconnect the complex circle
, which has topological dimension two instead of one.
As mentioned earlier, a line given by such a construction may or may not trisect the original angle
. But this trisection property can be expressed algebraically (e.g. using the triple angle formulae from trigonometry, or by building rotation matrices), and in particular makes sense over
. Thus, for any given construction of a line
, the set of
in
for which the construction is non-degenerate and trisects
is a constructible set (a boolean combination of algebraic sets). But
is an irreducible one-dimensional complex variety. As such, the aforementioned set of
is either generic (the complement of a dimension one algebraic set), or has dimension at most one. (Here we are implicitly using the fundamental theorem of algebra, because the basic dimension theory of algebraic geometry only works properly over algebraically closed fields.)
On the other hand, there are at most countably many constructions, and by hypothesis, for each choice of in
, at least one of these constructions has to trisect the angle. Applying the Baire category theorem (or countable additivity of Lebesgue measure, or using the algebraic geometry fact that an algebraic variety over an uncountable field cannot be covered by the union of countably many algebraic sets of smaller dimension), we conclude that there is a single construction which trisects the angle
for a generic choice of
, i.e. for all
in
outside of a finite set of points, there is a construction, which amongst its multiple possible values, is able to output at least one line
that trisects
.
Now one performs monodromy. Suppose we move around a closed loop in
that avoids all points of degeneracy. Then all the other points, lines, and circles constructed from
can be continuously extended from an initial configuration as discussed earlier, with each such object tracing out its own path in its own configuration space. Because of the presence of square roots in constructions such as the intersection (1) between two circles, or the intersection (2) between a circle and a line, these constructions may map a closed loop to an open loop; but because the square root function forms a double cover of
, we see that any closed loop in
, if doubled, will continue to be a closed loop upon taking a square root. (Alternatively, one can argue geometrically rather than algebraically, noting that in the intersection of (say) two non-degenerate circles
, there are only two possible choices for the intersection point of these two circles, and so if one performs monodromy along a loop of possible pairs
of circles, either these two choices return to where they initially started, or are swapped; so if one doubles the loop, one must necessarily leave the intersection points unchanged.) Iterating this, we see that any object constructed by straightedge and compass from
must have period
for some power of two
, in the sense that if one iterates a loop of
in
avoiding degenerate points
times, the object must return to where it started. (In more algebraic terminology: the monodromy group must be a
-group.)
Now, one traverses along a slight perturbation of a single rotation of the real unit circle
, taking a slight detour around the finite number of degeneracy points one encounters along the way. Since
has to trisect the angle
at each of these points, while varying continuously with
, we see that when
traverses a full rotation,
has only traversed one third of a rotation (or two thirds, depending on which trisection one obtained), and so the period of
must be a multiple of three; but this contradicts Lemma 2, and the claim follows.













146 comments
Comments feed for this article
12 April, 2017 at 4:24 am
Alex
Hi every one. Very interesting comments in here. I however strongly disagree with the statement that it is geometrically impossible to trisect any angle defined between two rays, uniting at a common end point. Looking at the angle trisection impossibility proof, Wantzel gave just a statement that it is impossible to classically trisect an angle, and to support his statement, he used a 60 degree angle as an example that no one can construct a 20 degree angle. I think this was a very wrong approach of the case. First, the algebraic proof turned the problem from geometrical into a purely algebraic one. That violates the governing rigor in verifying geometrical logic. It it is important we look at what is possible and what is impossible reasonably. The first drawback in the impossibility proof is that, i would kind of, accept the statement of angle trisection impossibility only if wantzel gave a geometrical approach, for trisecting an angle such as 72 degrees, that cannot trisect the 60 degree angle. I have done some work in geometry. In my first publication, i aimed at generating an algorithm to help that would help construct all whole number angles, their multiples and sub-multiple angles. In this my approach, though the work did not have a geometric proof, i realized that this did not solve the angle trisection problem. I later Generated an simple proof, close to the Archimedes theorem of angle trisection using a marked straightedge, to support my theorem, but too aiming at solving the angle trisection problem.
I later realized that did not solve the problem, though using the proposed method, one is logically able to construct all whole number angles starting from 1 degree. In this paper i also have shown how to trisect angles of 48 and 60, as a general proof for construction of all whole number angles. I moreover, have made another algorithm for trisection of an arbitrary angle. In this theorem, i discovered it is possible to trisect all angles, within a certain range of angle. I chose this set to represent a subset of all the angles. From this link: https://www.academia.edu/32310946/trisection.docx, one is able to see some of the results i generated using my algorithm, which i will be posting soon after the proof is published. These results represent two aspects; as any reader would like to know from a construction, that, does the method work for all angles or for a specific angle?. How accurate are the results?. Find out from the docx file.
19 April, 2017 at 8:39 am
Harold Florentino Latortue, PhD
I completely agree with you on Wantzel proof. His approach just did replace x=2cos(20) in the equation. There is no graphic reasons for it. The same equation can be use to show that the solutions can be obtained from x=Rsin(a/6) and Y=R[cos(a/6)-cos(a/2). Once you move the origin of the coordinate system to O(0, cos(a/2) the problem is moved from a cubic root to a square root.
19 April, 2017 at 10:03 pm
Alex
Dear Prof. HAROLD FLORENTINO LATORTUE. Am glad that you accept there is messy in the angle trisection proof. Thanks for your comment. I also like your algebraic approach. I have tried to follow your slides but got lost at around slide 21. The construction is getting tiresome from this point because of the many steps to be followed. I think it really would have been good to have a more shorter method. At this point i am not able to decisively say your construction is exact because i have not gotten the results. I will try it again and get back to you later. I invite you to view the results i got from this link; https://www.academia.edu/32310946/trisection.docx. I have managed to generate a 7 steps algorithm for trisecting an arbitrary angle. In this draft, i have presented the results based on accuracy. My algorithm is purely compass-straightedge construction, no arithmetics nor measurements involved. It works for all angles, whole number angles and non-whole number angles trisection.
20 April, 2017 at 3:02 am
Harold Florentino Latortue, PhD
Alex, I understand that it appears tiresome. The slides are parts of the complete book that I publish on Amazon: ‘Graphic trisection of an arbitrary angle’. https://www.amazon.com/Graphic-Trisection-arbitrary-angle-impossible/dp/0692870121/ref=pd_sbs_14_1?_encoding=UTF8&pd_rd_i=0692870121&pd_rd_r=WM69FD6TZBW9MFS5F509&pd_rd_w=21g8T&pd_rd_wg=gvqZu&psc=1&refRID=WM69FD6TZBW9MFS5F509 In this book, there is an explanation of ‘what you are doing’ in each step. Plus the algebraic proof of why this work. Slide 26 presents the results when the graphic method is compared to the algebraic method for various values of the angle.
I do abide to the rules of straightedge and compass
I you can provide an email address I will be glad to send you a PDF copy of the book.
Thanks for your interest
Florentino
13 April, 2017 at 11:01 pm
Alex
Hello!! I got something else on cube duplication. I got a very interesting approach of constructing a line of magnitude 1.2599… given a cube of a unit length. In the work i have rounded up this factor to 1.26, that i could proof its exactness. I do not believe it is good we confuse an inability with impossibility. I think the most difficult thing under the sun is to proof something to be impossible. As a physicist, i understand what it means by something being impossible. For one to proof an impossibility, we have to take into consideration all the laws of nature. Not just acceptance of statements that something is impossible. Any way, in this article, i have addressed my solution as an approximate construction because of the proof i employed. But, i think if one is able to provably construct the third root of 2, what importantly matters is the logic followed towards the solution, and not much of the generated value, though the results should agree with the set claim. The method works for both the compass-straightedge construction and the CAD methods. I used GeiGebra in generating the results. Here is the link “https://www.academia.edu/32406599/Geometrical_Duplication_of_a_Cube_An_Approximate_Solution_”. Any feedback is highly welcome. Correspond through the provided e-mail in the paper.
Thanks.
13 April, 2017 at 11:06 pm
Alex
https://www.academia.edu/32406599/Geometrical_Duplication_of_a_Cube_An_Approximate_Solution_
19 April, 2017 at 8:20 am
Harold Florentino Latortue, PhD
With humility, I am convince that many problem may have undiscovered solutions. By freeing one of the algebraic constraints of the trisection of an arbitrary angle, one can reduce it from a cubic root to a square root approach. I invite you to look this following approach that has great possibilities: https://www.slideshare.net/HAROLDFLORENTINOLATO/graphic-trisection-of-an-arbitrary-angle?qid=760850f0-17cf-42f8-b747-01bfbd225113&v=&b=&from_search=1
19 April, 2017 at 10:26 pm
Alex
Hi HAROLD FLORENTINO LATORTUE. I do not think it will be a good thing to bend any algebraic condition, based on the classical geometric view of things. No one can deny that; Euclidean geometry has its initial shape in nature and sharply shine than any other new development in academia. It will remain in existence. However, i believe, we need to appreciate the fact that, the traditional geometers solely worked out their findings using only compass and straightedge. The analytical interpretation of geometrical findings came later, due to interest by humans to work with specific quantities. Number systems was created. I deeper look at the ancient times work would reveal that, Euclid did not work with numbers, and instead, he used the term magnitude. He did not have nationalities such as root 2. Instead, he worked with incomparable. But he was able to construct a line of magnitude root of 2. I think, the most important consideration in today’s research is to have a methods, that precisely give clear results, when performed using both the traditional approaches, and in using the CAD approaches. I Do agree with you that the most difficult thing in the universe for humans is to proof something to be completely impossible. No matter the set conditions for a particular problem, we need to be sure and clear that impossibility does not mean the inability to solve a particular problem. For example, if we consider a quantity power, in mechanics, power is defined by energy per unit time. When someone say; it is not possible to create not destroy power, i think it is quite sensible. The nature agree with such a claim. It is possible, physically, to have almost two identical people competing to run up and down a system of stair cases, and to have one of them wining the race. Empirically, it can be proven from any good physics lab that, the equation V=IR is correct. Therefore agreeing with the statement that it is impossible to create power. What importantly the matter should be is the analogs employed in disproving something. Statements based on incomprehensible algebraic proofs make no sense.
20 April, 2017 at 3:16 am
Harold Florentino Latortue, PhD
I too use the CAD for precision in the graphic method for precision. I tested it using really arbitrary angle value, like 23.27 degree (possible with autocad). i do not bend any of the rules. Just straightedge and compass. The algebraic analysis using cos(3a) showed that the solutions for the trisections are at the intersects of arc circle when you consider an axe translation for your coordinates systems. (No rule broken).
Please provide an email address so I can forward you a PDF file.
20 April, 2017 at 5:41 am
Alex
alexkimuya23@gmail.com
20 April, 2017 at 5:57 am
Alex
Dear Prof. HAROLD FLORENTINO LATORTUE. Please use the email above. Got issues with my network connection.
20 April, 2017 at 6:21 am
Harold Florentino Latortue, PhD
sent
20 April, 2017 at 6:44 am
Alex
Thanks. Will have a serious look at the proofs.
4 May, 2017 at 7:39 pm
Charles Bennett
As a practical matter, you can do it to within your protractor’s precision by noting that
1/3 = 1/2 – 1/4 + 1/8 – 1/16 ……
and then patiently doing enough alternating bisections to get within the desired tolerance.
Although algebra class taught me to not waste time on this, I confess that I do think about Morley’s triangles on occasion.
4 May, 2017 at 8:38 pm
Anonymous
Charles,
Actually you can do it with a compass and a straightedge for any arbitrary angle without any iteration with the same precision ad PI = 3.1416 ie with results to 1/1000 (using autocad for measuring the angles) of a degree using the Flatortue Method. https://www.slideshare.net/HAROLDFLORENTINOLATO/graphic-trisection-of-an-arbitrary-angle?qid=760850f0-17cf-42f8-b747-01bfbd225113&v=&b=&from_search=1
The acuracy for trisecting the arc is 1/10000 ie. to the 4th decimal point.
Try it, you will be amazed. Dont get stuck to the idea that it was proven to be impossible to achieve.
12 May, 2017 at 3:55 am
Alex
Hi. I invite you all to find out how one can construct all the whole number angles, their multiples and sub-multiples from the link: http://homeworkhelpguru.com/mathematics-solutions. In this site, the provided tutorials would help one learn not only the classical construction of all whole number angles, but also the construction of the infinitely the many regular polygons, the geometric trisection of all whole number trisectible angles, and much more.
19 June, 2017 at 7:56 am
Elephant Rock
Okay, so as embarrassing as it is to be among the cranks submitting yet another solution to a problem shown not to have one, I can’t think of why this very simple seeming proof is not valid, so I’ll post it here. Maybe someone can explain…
Trisecting a *line segment* is easy. Make two line segments equidistant from and perpendicular to the angle’s vertex by striking an arc from the vertex and joining the intersections. Trisect both line segments on either side of the angle’s vertex. Now draw two lines connecting each third of the opposite trisected line segments such that both lines pass through the vertex.
https://drive.google.com/a/bookplates.com/file/d/0B0fQ0MCqU054NzJMQWFpRGRUZWM/view?usp=sharing
19 June, 2017 at 8:37 am
Elephant Rock
Oops. I just realized why this ‘proof’ is invalid. The problem with using the trisected line is that it doesn’t project onto the arc without distortion. The center angle will be different than the two sides. Repeating the mistake on the opposite side and connecting through the vertex doesn’t buy anything either. I guess I won’t quit my day job. LOL
19 June, 2017 at 11:31 pm
Alex
Hi Elephant Rock
I looked at your construction results and i could not connect the figures well. However, i must say that, the angle trisection problem is still an open challenge. What importantly people need to put into consideration is the conditions governing the solutions to the problem. Many people (since Wantzel’s time) seemingly overlook the most serious restriction that all classical geometric problems should be solely sought using only two tools: an unmarked straightedge and a compass.
The compass straightedge construction is such a serious restriction, and from this stem other constraints that: no measurements are allowed, and any geometric procedure should not involve arithmetic. In other words, to proof any geometric problem, one needs to consider that, the solution is deeply inherent from the construction. It has to be geometrical. The angle trisection solution is possible. I cannot, though not a mathematician, call myself a crank. Any one with passion in geometry can solve this problem provided he has the basic classical geometric knowledge. This is the only weapon. I would invite you to have a look at the article: “https://www.academia.edu/33497904/Short_Review_on_Classical_Construction_of_Whole_Number_Angles_and_The_Angle_Trisection_Problem_A_Compass-Straightedge_Construction_”. In this paper, i have discussed much on classical geometric constructions, the construction of all whole number angles, and the relationship between the classical construction of whole number angles and the angle trisection problem. I also have, in brief, shown the relation between classical geometry and the analytical geometry. There are also many other sources containing such information, from research articles to the Euclid’s elements. We have to understand why one has to be careful in saying it is generally impossible to solve a certain problem. How? This is the most difficult task to do on earth. we only can demonstrate, and in any case, we have to illustrate the impossibility to a problem based on the required framework of the solution. For instance, the wantzel’s proof involved both quadratic and cubic equations. This among other problems in the proof make it geometrically invalid.
21 August, 2017 at 3:09 am
Alex
Here are some more youtube links: https://www.youtube.com/watch?v=JNmlPqmuVIo
21 August, 2017 at 3:16 am
Alex
Please open the videos on youtube for clearity.
3 September, 2017 at 11:45 pm
Alex
Hi guys! Here is my angle trisection solution. In my view, the angle trisection problem is solvable. In-fact in a very simple way. But, before i provide the solution, i think it is good scientists, consider the conditions governing the angle trisection problem. In classical geometry, the use of trigonometry has no space. This only make sense in analytical geometry. Therefore, any solution involving the use of trigonometry, and the other mechanical methods aimed at solving the angle trisection problem are generally wrong. In my view, what maters as Euclid did in his works, is the analogs followed towards the solution. Here, any solution should reasonably agree with the set conventions. i.e, for example, the value of the factor PI is mostly used up to 3.142 accuracy. Having this consideration, i would like to share my paper addressing on the angle trisection problem via the link; https://cirworld.com/index.php/jam/article/view/6175. Your comments and constructive views are welcomed. Thanks.
20 September, 2017 at 12:28 am
Alex
Hi
I would like to point out some few things about some of my earlier posts on this blog as follows:
The above posted video links are specifically based in the construction of all whole number angles, and the trisection of the infinitely many trisectible angles. They are not meant for the angle trisection solution.
I have made some basic corrections made during the production of the paper available through the link: https://www.academia.edu/34455820/The_Angle_Trisection_Solution_A_Compass-Straightedge_Ruler_Construction_,
which present the angle trisection solution. It the earlier post, on page 6 of the paper, figures 3 and 4 were interchanged during the copy-editing process, which we did not get off during the proofreading stage. In annex-1, the line trisection procedure was misleading and a very important correction has been made. Thank you for those who contacted me on these corrections. Any academician would acknowledge that, paper production comes after the review process. And that, a paper going though a peer-review process does not make it a perfect one. So such basic errors are common. Please download the corrected version of the publication from:
https://www.academia.edu/34455820/The_Angle_Trisection_Solution_A_Compass-Straightedge_Ruler_Construction_
Thank you.
14 December, 2017 at 2:34 am
Alex
My New solution on Cube Duplication:
https://www.academia.edu/32406599/The_Cube_Duplication_Solution_A_Compass-straightedge_Ruler_Construction_
5 January, 2018 at 6:45 pm
Gary E. Schultz
TRISECTING THE ANGLE
A call to all geometers of the 3,500 year, Trisect the Angle grand challenge. The dogma of this ages old, false impossibility, is greatly exaggerated. N.B., interested geometers, your impossibility emperor has no clothes, and hasn’t had any for about fifty-two years. And it does not dignify one’s misinformation to demur to the higher and foggier ground of the Galois ethers, as, for example, Pierre Wantzel was want to do in his obviously flawed paper of 1837. We’re in serious need of an update here. And the lowly sixty degree triangle . . . seriously? Read ’em and weep . . .
Accordingly, it is my great pleasure to introduce to you and the world (and hidden in plain sight all this time since 1966) a man worthy of surely nothing less than the Fields Medal, Mr. Harry Cohen:
Click to access Scan-130117-0005.pdf
5 January, 2018 at 8:57 pm
Gary E. Schultz
Erratum, “And the lowly sixty degree angle . . .”
25 January, 2018 at 3:09 pm
Gary E. Schultz
So we have five thumbs-down pinheads, huh? Look, pinheads, I can only give you the information (the link), I can’t give you the brains to understand it. — GES
7 January, 2018 at 11:23 am
Rainer aus dem Spring
Dear Professoer Tao,
I have not read the whole thread and therefore I am not sure if somebody already mentioned:
Wantzel did not use Galois theory. Galois’ paper was first published in 1846 – nine years after Wantzel’s paper.
For a detailed history and elementary proofs of non-constructibility theorems (apart form the transcendence of pi) I recommend:
Craig Smorynski, “History of Mathematics – A Supplement”
Springer, 2000
A really nice book.
Best regards,
Rainer aus dem Spring
16 January, 2018 at 7:28 am
Push
I can think of an iterative approach to trisect an angle. It is as follows. 1/3 = 1/(1+2)=1/(2 (1+1/2))=(1/2) (1-1/2+1/4-1/8+..) is an infinite series =1/2-1/4+1/8-1/16+…. This implies first bisect the angle. Then bisect the bisected angle. Then bisect the first bisected angle and the second bisected angle. Repeat the process few times till required accuracy based on the series and we can trisect the given angle. One can repeat the same procedure for the other half of the angle.
8 February, 2018 at 3:40 am
Nebojsa Mitic
Attachments
https://www.geogebra.org/m/HQm7WwFk
on the ruler $AB\infty{_1}\infty{_2}$ , raises divider ADC where AB + AB = AC, ruler sets the angle $\alpha$
semi-line ruler $B\infty{_1}$ sliding on point E , the point A of ruler slides semi-line l , when point C is on the line n , we get the radius of the circle , we get the angle $\beta$
we have solved the tricection of any angle
Look at the construction protocol , or find the error if there is ….
23 March, 2018 at 2:38 am
Joc
Dear Terence, why are you not deleting all the useless crank comments? They are just fodder for future cranks to come here and ‘observe’ that no mathematician has ever refuted their ‘terrific’ (more like terrible) claim to fame. Sometimes, freedom of speech gets us nowhere… Besides, they could freely post their junk on their own blog.
18 April, 2018 at 7:12 am
Anonymous
Dear Joc
With the highest degree of respect, allow me to respond to this your post. I am glad to have read your thinking. I understand it is not wise to hijack someones blog, and above all, a respectful blog like this of Prof. Terence.
I am wondering of few things:
“why are you not deleting all the useless crank comments?” Why would you advice one on how to manage his blog?
” They are just fodder for future cranks to come here and ‘observe’ that no mathematician has ever refuted their ‘terrific’ (more like terrible) claim to fame.” Why have you not these terrific claim of fame? Why let someone else do it for you?
“Sometimes, freedom of speech gets us nowhere” If it was not for freedom of speech, would you have posted on this blog freely as you did? I think there is nothing wrong with freedom of speech.
“Besides, they could freely post their junk on their own blog.” How would you define your contents in the post. Any information of help? So between the other posts and the contents of your comment, which one is junk? Is this your blog so as to post your feelings and not information in here?
Please Note:
I got nothing personal with you. I only have problem with how you cannot control your emotions. I find it healthy when one develops the courage to share a concept in a forum as this.If there is any junk that should never cross the eyes and in the minds of the future generations, through this blog, is your post. You just discourage others without any constructive contribution! How would you feel if you were told you cannot do anything from the capacity of your thinking?
This is the harm you are causing the future generations. You are among those robbing them the freedom to think. You are among those who just read and believe, and this is destructive i suppose! Your thinking is self defeating in simple terms. If you had good interest on the generations to come, you would have expressed your reasoning in a more academic rigorous manner.
I do not think anyone is looking for fame in this forum. Those after fame are acting movies.
So please let people express their thinking. Share their ideas. I would be happy to have my posts as crank. But one thing i am certain of, they are miles smarter than what you post.
The future generations may be smarter than we are today. They would ponder much about what you write. They will come across your comment and wonder what problems you observed, and what solution you offered. It is just poor one would express emotions that reasoning. I was glad to read your comment.
18 April, 2018 at 7:19 am
Anonymous
Hi. I am posting the latest copy of my paper on the angle trisection solution, as published by Journal of Advances in Mathematics. I will soon upload a video on the YouTube exposing the developed algorithms. This paper presents the most accurate, and the most elegant solution on Angle trisection In Universe (The limit of human knowledge) today. I hope it is of much help to those doing their research in the related areas:
https://www.academia.edu/34455820/The_Angle_Trisection_Solution_A_Compass-Straightedge_Ruler_Construction_
https://cirworld.com/index.php/jam/article/view/6175
17 July, 2018 at 12:21 am
Alex M Kimuya
Hi, with all respect, i hope to present my classical geometric solution to this old ages problem to those who love mathematics, and with good understanding of the subject in here too.
I have been following the discussion on the trisection of an arbitrary angle problem.In summary:
A proof to the impossibility is wrong from the beginning to the end. This is my philosophical thinking. To prove an impossibility, one is required to demonstrate at least two thing:
1. We need to show that the particular problem does not exist, and so too is its solution.
2. We need to show that no human can resolve the problem if it does exist, and that would imply the limitations of our tools, from the classical tools of geometry in the case of the angle trisection, to use of technology.
First, an attempt to justify these things will just be self defeating. To prove the non-existence of a problem that is already defined in humans knowledge simply show the first mistake in thinking. Second, to prove that a particular problem got no solution and that no human can resolve it is also self defeating. One would should have an infinite capacity of knowledge to justify these claims too. Infact, one is required to have total understanding of the entire universe. This is the initial point of the messy in any proof of impossibility, and so is the Angle Trisection Impossibility proof.
Almost every scientific concept has some governing conditions. There are those restrictions governing the angle trisection problem, and many other problems in classical geometry:
That the problems should solely be sought using the classical tools of geometry; compass and unmarked straightedge.
Other restrictions in way, stem from this condition:
a. The proposed solution should have a finite number of construction steps.
b. The construction procedure should not have arithmetic.
c. There should be no measurements in the described procedure.
Importantly to observe is that, the construction algorithm should be contained in the confines of the first three postulates of Euclid’s Elements. The solution should have a proof of the concept or the logic employed generating the proposed procedure. This proof should however, be inherent from the construction either. This was the ways of Geometry by the early Greek’s mathematicians.
Note: A proof should not involve complex trigonometry or any other form of algebra for it to be correct.
Looking at the proposed geometric impossibility proof in here, is just wrong. It is really not geometrical. Any other form of proof, whether from Galois theory or from whichever area that does not begin from plane geometry is incorrect. We can use the modern speak to describe the problems but one has to be careful that our definitive descriptions of the subject is not aimed at tweaking people into the wrong understanding of the concept.
Any one who understand Euclidean geometry would agree with me. However, use of algebra is simply analysis.It is healthy. Having said the impossibility proof to the angle trisection solution is wrong and not valid to hold allegiance in stating the angle trisection problem as impossible, we now have to look at the other side of the coin. The problem require a solution and not just any solution. Since we are in a practical universe, we have to consider the accuracy of the work to hit meaningful degree. For example, 1/1000. In this, we would avoid what the skepticals call an eyeballing construction.
Exactness is just theoretical. No one would show exactness. Those immune to this reality can give an explanation of what they mean by exactness in practical geometry.
The solution: Having written this little i share to you some few video clips showing my shortest and most elegant general solution to the angle trisection puzzle. It obeys all the classical geometric conditions. No measurements not any adjustments. The solution too has two important conditions, that when understood one would accept the facts.
Follow the following YouTube Links to access the videos:
Thanks.
17 July, 2018 at 5:02 am
Anonymous
Reading your “Note: A proof should not involve complex trigonometry or any other form of algebra for it to be correct.” it reminds me this video:
Pity, you should have seen this when you were much younger or long time ago, you would have been somewhere else by now.
17 July, 2018 at 10:45 pm
Alex M Kimuya
HI,
I think something is not clear here. And this could be the reason for the misunderstanding if am correct. First, this video clip is immaterial in this context. And if it makes some sense, it only depicts your understanding of my post, and the entire problem of the angle trisection.
Before i respond to you, let me point something out here:
My posts are not meant to harm anyone, but ti convey a concept. So no need to act emotionally. Your pity cannot work against a reality. If i am wrong, correct my contents.About where i am, or what i am, it is not at all important here too. As a fact, i am not that young and nor am i that old. I am comfortable with what i do too so let this not bother anyone like you. Let us speak and write science.
Back To Your Video
Analyzing what the physicist is saying, the general thing is understanding what problem in particular one is working on. But, this make no sense because it has no connection to:
“Note: A proof should not involve complex trigonometry or any other form of algebra for it to be correct.”
If it makes meaning here, it simply means the person not understanding the thing is you. Remember i have not created any rules and my argument is based on rules established may years possibly before even you, came to exist In simple terms, i meant that a proof does not have to be complex for it to be credited correct.In the case of Angle Trisection, it has to be inherent from the construction, and well geometrically founded before we introduce any other form of analysis. I am not against use of Algebra, but, if it is applied in a misleading manner that has to be refuted.
I got much understanding of Algebra too but what is the sense of using complex mathematics unnecessarily? The solution require to be proven geometrically. I also understand the angle trisection problem well so if there is someone lost in this context it probably could be you and any other person, with no proper reasons, is believing the impossibility proofs.
The fact that something is said by a renowned person, it does not mean it is final and no other human can talk about it. Some of the things from these people are not proven. When you post a video clip with just non-scientific statements and expect people to fear thinking is just waste of time and energy. People see the problems in the angle trisection impossibility proof. To justify this i refer you to this very blog: Why did Prof Terence Tao attempt a geometrical approach to justify the impossibility proof?
I acknowledge his approach and it simply shows Wantzel’s proof is not geometrical in the first place.
I hope you get sense as to why you need to redeem back your freedom of thinking and stop believing we possibly can proof impossibilities. We got much to do in science to change this planet for and make it better for the coming generations. Otherwise with people of your type, we wont progress. I could much appreciate if you posted your own video clip countering my arguments. Else, it just shows how poor some people are. A statement that can not be supported make no sense at all. Stop thinking you can create fear to the young researchers.
Thanks.
20 July, 2018 at 4:08 am
Alex M Kimuya
The Cube Duplication Solution
12 October, 2018 at 10:00 am
Miller’s Quadsector Theorem – Glimpses of Infinity, Reminders of Reality
[…] went for quadsectors instead – bisect and bisect again. (fascinating and unknowing nod to the futile attempts to trisect an angle using straight-edge and compass). Excitement fizzed around the room at the new […]
27 December, 2018 at 2:40 pm
Nest
What if the exception trisection of a straight angle could be used as a benchmark to trisect any angle?
In your Gallois-Wantzel demonstration you did not explain the nature of exceptional angles.
Is it possible to demonstrate that using a pi/2 angle as trisection benchmark is not a door to trisecting any angle?
28 December, 2018 at 4:24 am
Anonymous
Actually, the set of “trisectable angles” (i.e. that can be trisected by straightedge and compass – which is equivalent to be constructible from the integers using only finitely many four basic arithmetical operations and square root extractions) contains (but not limited to) all the angles of the form where
where 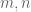 are positive integers.
are positive integers.![[0, \pi]](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cpi%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
Which implies that this set of “trisectable angles” is dense in
It would be interesting to give a more explicit characterization for this exceptional set of “trisectable angles” .
20 February, 2019 at 10:49 am
Richard Mangel
Start by constructing a circle, then construct a circle atop the first circle, construct one vertical line through the center’s of the circles, then draw horizontal lines through the circles. Connect the south point of the bottom circle with the west point of the top circle. The left radius of the circle is cut in one-third and two-thirds, respectively.
To trisect an angle, increase the circles up, as many as you want, then above for odd reciprocals, fill circles with additional circles with horizonal tangents where circles meet. (All circles have radius of one.). Angles are addition of angles. Only need. . . . Proportional sides, take square root. Get trigometric answer to lower angle of right triangle by looking up in trig table, or do the division. Add this to simple angle such as seven and one-half, twelve and one-half,etc. This sum of angles is the unknown angle. To then trisect the known angle, cut pieces of pie into fractional parts need not be degrees. Add parts as needed. he.1 2 1/2 + 7 1/2 equals 20 parts. 33 1/3 + 33 1/3 + 33 1/3 equals 100 percent of the 360 degree pie.
5 June, 2019 at 7:36 pm
Fermat Primes and the Gauss-Wantzel Theorem - AMSI Vacation Research Scholarships 2018/19
[…] https://terrytao.wordpress.com/2011/08/10/a-geometric-proof-of-the-impossibility-of-angle-trisection… […]
14 June, 2019 at 10:47 am
Joshua Robinson
I Trisected any angle and it looks like ur proofs
https://www.youtube.com/channel/UC0pmyIMkgexU3vtvTFUSMfw
Please look.
14 June, 2019 at 8:01 pm
paulsancheski
By Jove, I think you’ve got it! But will have to review further …
16 June, 2019 at 7:20 am
paulsancheski
Sorry, Joshua, but we have to call off the parade. A trigonometric analysis applying your method to a sixty-degree angle indicates your trisectors are around 20.104-degrees from the angle arms, off by a little over a tenth of a degree. Good try. Have a cigar anyway.
15 September, 2019 at 8:33 pm
Foundations of Arithmetic
Is it possible any modern tools in arithmetic can say anything about ‘Suppose that a linear time Turing Machine computes the first {n} digits of the real number {r} in base ten. Then, the number is either a rational number or a transcendental number’ mentioned in https://rjlipton.wordpress.com/2012/06/15/why-the-hartmanis-stearns-conjecture-is-still-open/?
15 September, 2019 at 11:07 pm
Foundations of Arithmetic
Also https://rjlipton.wordpress.com/2009/02/24/a-conjecture-of-hartmanis/ and https://rjlipton.wordpress.com/2012/06/04/transcendental-aspects-of-turing-machines/.
16 September, 2019 at 1:11 pm
Foundations of Arithmetic
This also appears interesting https://mathoverflow.net/questions/288911/any-proved-connection-between-roth-theorem-and-hartmanis-stearns-conjecture. This is the fundamental reference https://fi.ort.edu.uy/innovaportal/file/20124/1/60-hartmanis_stearns_complexity_of_algorithms.pdf.
16 September, 2019 at 1:34 pm
Foundations of Arithmetic
Summary https://www.cs.auckland.ac.nz/research/conferences/wtcs2012/resources/Freivalds-Rusins.pdf.
16 September, 2019 at 8:26 am
real analytic
The simplest application of this method, which was also done to avoid field theory, is JH Conway’s meta-proof that there is no “direct” solution of the Steiner-Lehmus problem (to show that equal angle bisectors imply equal sides in a triangle).
The S-L theorem is false over general fields, which is a field theoretic argument that there is no proof by equality chasing. Indeed the usual proofs rely on order properties of the positive reals; they proceed by case analysis to rule out a > b and a < b, rather than proving a=b directly.
Conway replaced field theory by R-to-R analytic continuation, passing points through each other, again with complexification as the tacit justification. The continuation allows some of the side lengths to flip sign and exchanges interior and exterior angle bisectors, resulting in a configuration where the analytically continued interpretation of the statement becomes false.
On the other hand the inequality arguments do work in intuitionistic logic, without having to do case analysis based on Excluded Middle, so this still leaves the problem of rigorously specifying what constitutes a "direct proof".
19 October, 2019 at 10:12 pm
Ronald Davis
With ten nickels, make an equilateral triangle. From the center point of a corner nickel imagine two radiated lines from there, radiating out through the two points where the row of three, touch, and beyond… add the two triangle lines, on the outside headed in the same direction and Wallah, you just trisected your first triangle. To trisect other angles send me an email and I will send you… How To trisect.. Or just think about the geometry of when lines radiate to a point, and radii is doubled as perpendicular lines one, to two, to four… (and clear to six and nine, which divide by threes nicely); it make radiated lines spread outward… but there is also a 3 in-between 2 and 4, when radiating… I really can trisect an angle! …Look at your four finger with one eye, and imagine three lines from your eye out through the cracks between your fingers… “read between the lines as they say, four fingers, but three lines! I am almost 81 years… So I’m giving this Info., away to all… [However I do have my date for creativity covered, for how I trisect] I have other stuff if you like Physics and Geometry, that got lost, or too quickly passed in Classical Physics… Ron Davis radpressure@gmail.com
28 December, 2019 at 10:28 am
Anonymous
Ive solved it, but not for all angles,, any one interested, ill send it to you .The question is what can u use it for. markusbolin@gmail.com
1 June, 2020 at 11:02 pm
fernando mancebo
I think angle trisection is very easy and fast only with compass.
16 August, 2020 at 5:39 pm
Taha M. Muhammad
I trisected angles. Please look at you tube.
I’m using the same method which is 1, 2, 3 and Trisecting angles of 0 to 360 degrees.
I am not deviding 2 by 3.
15 December, 2020 at 9:45 pm
Anonymous
https://www.facebook.com/photo?fbid=1803820016439648&set=a.397252653763065
5 February, 2022 at 3:50 am
Luis Martinez
GEOMETRIC PROOF of the 60º angle trisection with ruler and compass.
The trigonometric expression is determined in the form:
With c opposite side to the angle to be trisected.
It includes:
Method to split any segment into three ( with compass).
Method to multiply any angle (with compas)
7 October, 2022 at 11:22 pm
Mahesh R Bubna
After putting 40-42 years efforts I have been to trisect an arbitrary angle to an unprecedent/ miraculous approximation, that too, using only a compass and an unmarked straight edge with 9-10 finite easy steps, for example
30° to 10.000000°
36° to 12.000000°
40° to 13.333333°
45° to 14.999999° and so on…..
The images of the above are ready for uploading…..
23 January, 2023 at 8:09 am
Luis Martinez
The Trisection method for the rule and the compass, the 20º angles is defined in the triangle of sides (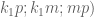 .
.
By trigonometry:
The greater the value of (x) in the greater the number of decimal places with its absolute value (see youtube vedeo).
the greater the number of decimal places with its absolute value (see youtube vedeo).
And
The greater the value of (x) in the greater the number of decimal places with its absolute value.
the greater the number of decimal places with its absolute value.
Professor Tao: As a math genious, I hope the you so proceed.
23 January, 2023 at 8:48 am
Mahesh Bubna
The new is that 99.99â approximation that too by using only a compass and an unmarked straightedge with 5-6 ascertain steps is first time in last 2250 years and that has become possible by only and anly one method invented by me.
23 January, 2023 at 12:36 pm
Anonymous
This comment could be written only by a very modest person!
12 February, 2023 at 7:16 am
luis martinez
where: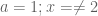
With a = 1 and x = 2 we have:
12 February, 2023 at 9:06 pm
Mahesh Bubna
Yes, I know that exact trisection of a given angle is impossible. But what about the MRB method, invented by me, which (using only a compass -straightedge) gives 99.99+â approximation.
26 February, 2023 at 7:15 am
Luis Martinez
The root of with ruler and compas by (ENFER DIEZ).
with ruler and compas by (ENFER DIEZ).
Today sunday one day amomg many open minds.
With the segment and unit; the root of
and unit; the root of  is determine in the form:
is determine in the form:
$latex\sqrt{\pi} = 6 – 3\sqrt{2} + \frac{6 – 4\sqrt{2}}{3^{3}} + 2\left[\frac{6 – 4\sqrt{2}}{3^{5}}\right]$ –
$\latex\sqrt{\pi} = 6 – 3\sqrt{2} + \frac{6 – 4\sqrt{2}}{3^{3}} + 2\left[\frac{6 – 4\sqrt{2}}{3^{5}}\right] – \frac{6 – 4\sqrt{2}}{3^{5}*2^{2}}$ –
{3^{8}*2^{13}}$ +
28 February, 2023 at 3:05 am
Anonymous
I recommend the book:Solving problem in Number Theory and Geometry.
28 February, 2023 at 7:50 am
Luis Martinez
As last information; the third problem.
The![\sqrt[3]{2}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B2%7D&bg=ffffff&fg=545454&s=0&c=20201002) with ruler and compas:
with ruler and compas:
With n = 2
The greater n is, the greater the number of zeros.
7 March, 2023 at 10:12 am
Md Mahabub Alam
It is possible trisection any angle by compass. It’s possible for me.plesse help me for published it.
19 January, 2024 at 12:32 pm
Anonymous
I, Mahesh R Bubna, has been successful in trisecting an arbitrary angle by using only a compass and straightedge to the approximation correct up to 6+ decimals.
One can refer Angle Trisection by Mahesh R Bubna on LinkedIn.