Monthly Archive

You are currently browsing the monthly archive for November 2018.

Embedding the Heisenberg group into a bounded dimensional Euclidean space with optimal distortion

26 November, 2018 in math.AP, math.MG, paper | Tags: , , | by | 13 comments

I’ve just uploaded to the arXiv my paper “Embedding the Heisenberg group into a bounded dimensional Euclidean space with optimal distortion“, submitted to Revista Matematica Iberoamericana. This paper concerns the extent to which one can accurately embed the metric structure of the Heisenberg group

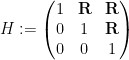
\displaystyle H := \begin{pmatrix} 1 & {\bf R} & {\bf R} \\ 0 & 1 & {\bf R} \\ 0 & 0 & 1 \end{pmatrix}

into Euclidean space, which we can write as {\{ [x,y,z]: x,y,z \in {\bf R} \}} with the notation

\displaystyle [x,y,z] := \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{pmatrix}.

Here we give {H} the right-invariant Carnot-Carathéodory metric {d} coming from the right-invariant vector fields

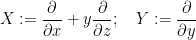
\displaystyle X := \frac{\partial}{\partial x} + y \frac{\partial}{\partial z}; \quad Y := \frac{\partial}{\partial y}

but not from the commutator vector field

\displaystyle Z := [Y,X] = \frac{\partial}{\partial z}.

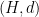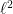This gives {H} the geometry of a Carnot group. As observed by Semmes, it follows from the Carnot group differentiation theory of Pansu that there is no bilipschitz map from {(H,d)} to any Euclidean space {{\bf R}^D} or even to {\ell^2}, since such a map must be differentiable almost everywhere in the sense of Carnot groups, which in particular shows that the derivative map annihilate 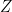{Z} almost everywhere, which is incompatible with being bilipschitz.

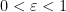On the other hand, if one snowflakes the Heisenberg group by replacing the metric {d} with {d^{1-\varepsilon}} for some {0 < \varepsilon < 1}, then it follows from the general theory of Assouad on embedding snowflaked metrics of doubling spaces that 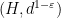{(H,d^{1-\varepsilon})} may be embedded in a bilipschitz fashion into 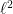{\ell^2}, or even to 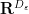{{\bf R}^{D_\varepsilon}} for some {D_\varepsilon} depending on {\varepsilon}.

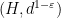Of course, the distortion of this bilipschitz embedding must degenerate in the limit {\varepsilon \rightarrow 0}. From the work of Austin-Naor-Tessera and Naor-Neiman it follows that {(H,d^{1-\varepsilon})} may be embedded into 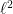{\ell^2} with a distortion of 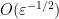{O( \varepsilon^{-1/2} )}, but no better. 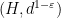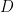The Naor-Neiman paper also embeds {(H,d^{1-\varepsilon})} into a finite-dimensional space {{\bf R}^D} with {D} independent of {\varepsilon}, but at the cost of worsening the distortion to {O(\varepsilon^{-1})}. They then posed the question of whether this worsening of the distortion is necessary.

The main result of this paper answers this question in the negative:

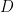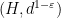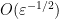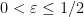Theorem 1 There exists an absolute constant {D} such that {(H,d^{1-\varepsilon})} may be embedded into {{\bf R}^D} in a bilipschitz fashion with distortion {O(\varepsilon^{-1/2})} for any {0 < \varepsilon \leq 1/2}.

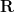To motivate the proof of this theorem, let us first present a bilipschitz map {\Phi: {\bf R} \rightarrow \ell^2} from the snowflaked line {({\bf R},d_{\bf R}^{1-\varepsilon})} (with {d_{\bf R}} being the usual metric on {{\bf R}}) into complex Hilbert space {\ell^2({\bf C})}. The map is given explicitly as a Weierstrass type function

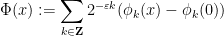
\displaystyle \Phi(x) := \sum_{k \in {\bf Z}} 2^{-\varepsilon k} (\phi_k(x) - \phi_k(0))

where for each 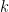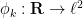{k}, {\phi_k: {\bf R} \rightarrow \ell^2} is the function

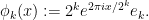
\displaystyle \phi_k(x) := 2^k e^{2\pi i x / 2^k} e_k.

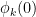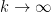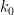and {(e_k)_{k \in {\bf Z}}} are an orthonormal basis for {\ell^2({\bf C})}. The subtracting of the constant {\phi_k(0)} is purely in order to make the sum convergent as {k \rightarrow \infty}. If {x,y \in {\bf R}} are such that {2^{k_0-2} \leq d_{\bf R}(x,y) \leq 2^{k_0-1}} for some integer {k_0}, one can easily check the bounds

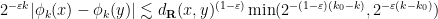
\displaystyle 2^{-\varepsilon k}|\phi_k(x) - \phi_k(y)| \lesssim d_{\bf R}(x,y)^{(1-\varepsilon)} \min( 2^{-(1-\varepsilon) (k_0-k)}, 2^{-\varepsilon (k-k_0)} )

with the lower bound

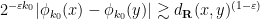
\displaystyle 2^{-\varepsilon k_0}|\phi_{k_0}(x) - \phi_{k_0}(y)| \gtrsim d_{\bf R}(x,y)^{(1-\varepsilon)}

at which point one finds that

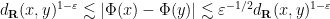
\displaystyle d_{\bf R}(x,y)^{1-\varepsilon} \lesssim |\Phi(x) - \Phi(y)| \lesssim \varepsilon^{-1/2} d_{\bf R}(x,y)^{1-\varepsilon}

as desired.

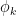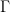The key here was that each function {\phi_k} oscillated at a different spatial scale {2^k}, and the functions were all orthogonal to each other (so that the upper bound involved a factor of {\varepsilon^{-1/2}} rather than {\varepsilon^{-1}}). One can replicate this example for the Heisenberg group without much difficulty. Indeed, if we let {\Gamma := \{ [a,b,c]: a,b,c \in {\bf Z} \}} be the discrete Heisenberg group, then the nilmanifold {H/\Gamma} is a three-dimensional smooth compact manifold; thus, by the Whitney embedding theorem, it smoothly embeds into {{\bf R}^6}. 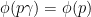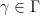This gives a smooth immersion {\phi: H \rightarrow {\bf R}^6} which is {\Gamma}-automorphic in the sense that {\phi(p\gamma) = \phi(p)} for all {p \in H} and {\gamma \in \Gamma}. If one then defines {\phi_k: H \rightarrow \ell^2 \otimes {\bf R}^6} to be the function

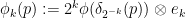
\displaystyle \phi_k(p) := 2^k \phi( \delta_{2^{-k}}(p) ) \otimes e_k

where {\delta_\lambda: H \rightarrow H} is the scaling map

\displaystyle \delta_\lambda([x,y,z]) := [\lambda x, \lambda y, \lambda^2 z],

then one can repeat the previous arguments to obtain the required bilipschitz bounds

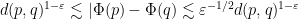
\displaystyle d(p,q)^{1-\varepsilon} \lesssim |\Phi(p) - \Phi(q) \lesssim \varepsilon^{-1/2} d(p,q)^{1-\varepsilon}

for the function

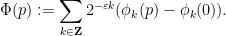
\displaystyle \Phi(p) :=\sum_{k \in {\bf Z}} 2^{-\varepsilon k} (\phi_k(p) - \phi_k(0)).

To adapt this construction to bounded dimension, the main obstruction was the requirement that the 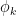{\phi_k} took values in orthogonal subspaces. But if one works things out carefully, it is enough to require the weaker orthogonality requirement

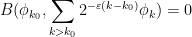
\displaystyle B( \phi_{k_0}, \sum_{k>k_0} 2^{-\varepsilon(k-k_0)} \phi_k ) = 0

for all 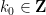{k_0 \in {\bf Z}}, where {B(\phi, \psi): H \rightarrow {\bf R}^2} is the bilinear form

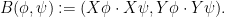
\displaystyle B(\phi,\psi) := (X \phi \cdot X \psi, Y \phi \cdot Y \psi ).

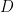One can then try to construct the {\phi_k: H \rightarrow {\bf R}^D} for bounded dimension {D} by an iterative argument. After some standard reductions, the problem becomes this (roughly speaking): given a smooth, slowly varying function 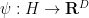{\psi: H \rightarrow {\bf R}^{D}} whose derivatives obey certain quantitative upper and lower bounds, construct a smooth oscillating function {\phi: H \rightarrow {\bf R}^{D}}, whose derivatives also obey certain quantitative upper and lower bounds, which obey the equation

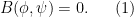
\displaystyle B(\phi,\psi) = 0. \ \ \ \ \ (1)

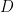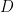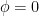We view this as an underdetermined system of differential equations for {\phi} (two equations in {D} unknowns; after some reductions, our {D} can be taken to be the explicit value {36}). The trivial solution {\phi=0} to this equation will be inadmissible for our purposes due to the lower bounds we will require on {\phi} (in order to obtain the quantitative immersion property mentioned previously, as well as for a stronger “freeness” property that is needed to close the iteration). 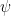Because this construction will need to be iterated, it will be essential that the regularity control on {\phi} is the same as that on {\psi}; one cannot afford to “lose derivatives” when passing from 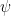{\psi} to {\phi}.

This problem has some formal similarities with the isometric embedding problem (discussed for instance in this previous post), which can be viewed as the problem of solving an equation of the form 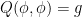{Q(\phi,\phi) = g}, where 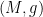{(M,g)} is a Riemannian manifold and 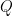{Q} is the bilinear form

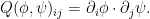
\displaystyle Q(\phi,\psi)_{ij} = \partial_i \phi \cdot \partial_j \psi.

The isometric embedding problem also has the key obstacle that naive attempts to solve the equation 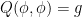{Q(\phi,\phi)=g} iteratively can lead to an undesirable “loss of derivatives” that prevents one from iterating indefinitely. This obstacle was famously resolved by the Nash-Moser iteration scheme in which one alternates between perturbatively adjusting an approximate solution to improve the residual error term, and mollifying the resulting perturbation to counteract the loss of derivatives. The current equation (1) differs in some key respects from the isometric embedding equation 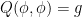{Q(\phi,\phi)=g}, in particular being linear in the unknown field {\phi} rather than quadratic; nevertheless the key obstacle is the same, namely that naive attempts to solve either equation lose derivatives. Our approach to solving (1) was inspired by the Nash-Moser scheme; in retrospect, I also found similarities with Uchiyama’s constructive proof of the Fefferman-Stein decomposition theorem, discussed in this previous post (and in this recent one).

To motivate this iteration, we first express 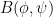{B(\phi,\psi)} using the product rule in a form that does not place derivatives directly on the unknown {\phi}:

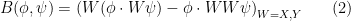
\displaystyle B(\phi,\psi) = \left( W(\phi \cdot W \psi) - \phi \cdot WW \psi\right)_{W = X,Y} \ \ \ \ \ (2)

This reveals that one can construct solutions {\phi} to (1) by solving the system of equations

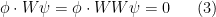
\displaystyle \phi \cdot W \psi = \phi \cdot WW \psi = 0 \ \ \ \ \ (3)

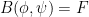for {W \in \{X, Y \}}. Because this system is zeroth order in {\phi}, this can easily be done by linear algebra (even in the presence of a forcing term {B(\phi,\psi)=F}) if one imposes a “freeness” condition (analogous to the notion of a free embedding in the isometric embedding problem) that {X \psi(p), Y \psi(p), XX \psi(p), YY \psi(p)} are linearly independent at each point {p}, which (together with some other technical conditions of a similar nature) one then adds to the list of upper and lower bounds required on {\psi} (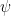with a related bound then imposed on {\phi}, in order to close the iteration). 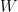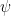However, as mentioned previously, there is a “loss of derivatives” problem with this construction: due to the presence of the differential operators {W} in (3), a solution {\phi} constructed by this method can only be expected to have two degrees less regularity than {\psi} at best, which makes this construction unsuitable for iteration.

To get around this obstacle (which also prominently appears when solving (linearisations of) the isometric embedding equation 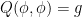{Q(\phi,\phi)=g}), we instead first construct a smooth, low-frequency solution {\phi_{\leq N_0} \colon H \rightarrow {\bf R}^{D}} to a low-frequency equation

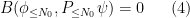
\displaystyle B( \phi_{\leq N_0}, P_{\leq N_0} \psi ) = 0 \ \ \ \ \ (4)

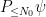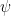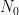where {P_{\leq N_0} \psi} is a mollification of {\psi} (of Littlewood-Paley type) applied at a small spatial scale {1/N_0} for some {N_0}, and then gradually relax the frequency cutoff {P_{\leq N_0}} to deform this low frequency solution {\phi_{\leq N_0}} to a solution {\phi} of the actual equation (1).

We will construct the low-frequency solution {\phi_{\leq N_0}} rather explicitly, using the Whitney embedding theorem to construct an initial oscillating map {f} into a very low dimensional space {{\bf R}^6}, composing it with a Veronese type embedding into a slightly larger dimensional space {{\bf R}^{27}} to obtain a required “freeness” property, and then composing further with a slowly varying isometry {U(p) \colon {\bf R}^{27} \rightarrow {\bf R}^{36}} depending on {P_{\leq N_0}} and constructed by a quantitative topological lemma (relying ultimately on the vanishing of the first few homotopy groups of high-dimensional spheres), in order to obtain the required orthogonality (4). (This sort of “quantitative null-homotopy” was first proposed by Gromov, with some recent progress on optimal bounds by Chambers-Manin-Weinberger and by Chambers-Dotterer-Manin-Weinberger, but we will not need these more advanced results here, as one can rely on the classical qualitative vanishing {\pi^k(S^d)=0} for {k < d} together with a compactness argument to obtain (ineffective) quantitative bounds, which suffice for this application).

To perform the deformation of {\phi_{\leq N_0}} into {\phi}, we must solve what is essentially the linearised equation

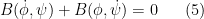
\displaystyle B( \dot \phi, \psi ) + B( \phi, \dot \psi ) = 0 \ \ \ \ \ (5)

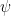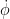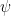of (1) when {\phi}, {\psi} (viewed as low frequency functions) are both being deformed at some rates {\dot \phi, \dot \psi} (which should be viewed as high frequency functions). To avoid losing derivatives, the magnitude of the deformation {\dot \phi} in {\phi} should not be significantly greater than the magnitude of the deformation {\dot \psi} in {\psi}, when measured in the same function space norms.

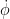As before, if one directly solves the difference equation (5) using a naive application of (2) with {B(\phi,\dot \psi)} treated as a forcing term, one will lose at least one derivative of regularity when passing from {\dot \psi} to {\dot \phi}. However, observe that (2) (and the symmetry {B(\phi, \dot \psi) = B(\dot \psi,\phi)}) can be used to obtain the identity

\displaystyle B( \dot \phi, \psi ) + B( \phi, \dot \psi ) = \left( W(\dot \phi \cdot W \psi + \dot \psi \cdot W \phi) - (\dot \phi \cdot WW \psi + \dot \psi \cdot WW \phi)\right)_{W = X,Y} \ \ \ \ \ (6)

and then one can solve (5) by solving the system of equations

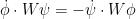
\displaystyle \dot \phi \cdot W \psi = - \dot \psi \cdot W \phi

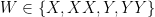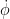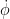for {W \in \{X,XX,Y,YY\}}. The key point here is that this system is zeroth order in both {\dot \phi} and {\dot \psi}, so one can solve this system without losing any derivatives when passing from {\dot \psi} to {\dot \phi}; compare this situation with that of the superficially similar system

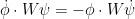
\displaystyle \dot \phi \cdot W \psi = - \phi \cdot W \dot \psi

that one would obtain from naively linearising (3) without exploiting the symmetry of 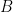{B}. There is still however one residual “loss of derivatives” problem arising from the presence of a differential operator 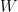{W} on the {\phi} term, which prevents one from directly evolving this iteration scheme in time without losing regularity in {\phi}. It is here that we borrow the final key idea of the Nash-Moser scheme, which is to replace {\phi} by a mollified version {P_{\leq N} \phi} of itself (where the projection {P_{\leq N}} depends on the time parameter). 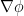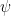This creates an error term in (5), but it turns out that this error term is quite small and smooth (being a “high-high paraproduct” of {\nabla \phi} and {\nabla\psi}, it ends up being far more regular than either {\phi} or {\psi}, even with the presence of the derivatives) and can be iterated away provided that the initial frequency cutoff 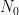{N_0} is large and the function 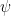{\psi} has a fairly high (but finite) amount of regularity (we will eventually use the Hölder space 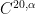{C^{20,\alpha}} on the Heisenberg group to measure this).

The nonlinearity of the Fefferman-Stein decomposition

21 November, 2018 in expository, math.CA, math.FA | Tags: , | by | 12 comments

The celebrated decomposition theorem of Fefferman and Stein shows that every function {f \in \mathrm{BMO}({\bf R}^n)} of bounded mean oscillation can be decomposed in the form

\displaystyle f = f_0 + \sum_{i=1}^n R_i f_i \ \ \ \ \ (1)

 

modulo constants, for some {f_0,f_1,\dots,f_n \in L^\infty({\bf R}^n)}, where {R_i := |\nabla|^{-1} \partial_i} are the Riesz transforms. A technical note here a function in BMO is defined only up to constants (as well as up to the usual almost everywhere equivalence); related to this, if {f_i} is an {L^\infty({\bf R}^n)} function, then the Riesz transform {R_i f_i} is well defined as an element of {\mathrm{BMO}({\bf R}^n)}, but is also only defined up to constants and almost everywhere equivalence.

The original proof of Fefferman and Stein was indirect (relying for instance on the Hahn-Banach theorem). A constructive proof was later given by Uchiyama, and was in fact the topic of the second post on this blog. A notable feature of Uchiyama’s argument is that the construction is quite nonlinear; the vector-valued function {(f_0,f_1,\dots,f_n)} is defined to take values on a sphere, and the iterative construction to build these functions from {f} involves repeatedly projecting a potential approximant to this function to the sphere (also, the high-frequency components of this approximant are constructed in a manner that depends nonlinearly on the low-frequency components, which is a type of technique that has become increasingly common in analysis and PDE in recent years).

It is natural to ask whether the Fefferman-Stein decomposition (1) can be made linear in {f}, in the sense that each of the {f_i, i=0,\dots,n} depend linearly on {f}. Strictly speaking this is easily accomplished using the axiom of choice: take a Hamel basis of {\mathrm{BMO}({\bf R}^n)}, choose a decomposition (1) for each element of this basis, and then extend linearly to all finite linear combinations of these basis functions, which then cover {\mathrm{BMO}({\bf R}^n)} by definition of Hamel basis. But these linear operations have no reason to be continuous as a map from {\mathrm{BMO}({\bf R}^n)} to {L^\infty({\bf R}^n)}. So the correct question is whether the decomposition can be made continuously linear (or equivalently, boundedly linear) in {f}, that is to say whether there exist continuous linear transformations {T_i: \mathrm{BMO}({\bf R}^n) \rightarrow L^\infty({\bf R}^n)} such that

\displaystyle f = T_0 f + \sum_{i=1}^n R_i T_i f \ \ \ \ \ (2)

 

modulo constants for all {f \in \mathrm{BMO}({\bf R}^n)}. Note from the open mapping theorem that one can choose the functions {f_0,\dots,f_n} to depend in a bounded fashion on {f} (thus {\|f_i\|_{L^\infty} \leq C \|f\|_{BMO}} for some constant {C}, however the open mapping theorem does not guarantee linearity. Using a result of Bartle and Graves one can also make the {f_i} depend continuously on {f}, but again the dependence is not guaranteed to be linear.

It is generally accepted folklore that continuous linear dependence is known to be impossible, but I had difficulty recently tracking down an explicit proof of this assertion in the literature (if anyone knows of a reference, I would be glad to know of it). The closest I found was a proof of a similar statement in this paper of Bourgain and Brezis, which I was able to adapt to establish the current claim. The basic idea is to average over the symmetries of the decomposition, which in the case of (1) are translation invariance, rotation invariance, and dilation invariance. This effectively makes the operators {T_0,T_1,\dots,T_n} invariant under all these symmetries, which forces them to themselves be linear combinations of the identity and Riesz transform operators; however, no such non-trivial linear combination maps {\mathrm{BMO}} to {L^\infty}, and the claim follows. Formal details of this argument (which we phrase in a dual form in order to avoid some technicalities) appear below the fold.

Read the rest of this entry »

Archives