Venn and Euler type diagrams for vector spaces and abelian groups

A popular way to visualise relationships between some finite number of sets is via Venn diagrams, or more generally Euler diagrams. In these diagrams, a set is depicted as a two-dimensional shape such as a disk or a rectangle, and the various Boolean relationships between these sets (e.g., that one set is contained in another, or that the intersection of two of the sets is equal to a third) is represented by the Boolean algebra of these shapes; Venn diagrams correspond to the case where the sets are in “general position” in the sense that all non-trivial Boolean combinations of the sets are non-empty. For instance to depict the general situation of two sets together with their intersection and one might use a Venn diagram such as

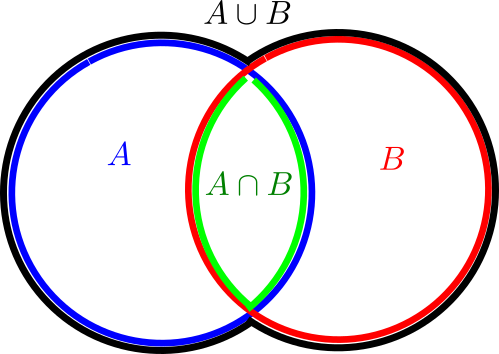
(where we have given each region depicted a different color, and moved the edges of each region a little away from each other in order to make them all visible separately), but if one wanted to instead depict a situation in which the intersection was empty, one could use an Euler diagram such as

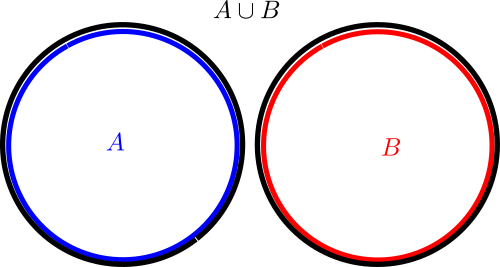
One can use the area of various regions in a Venn or Euler diagram as a heuristic proxy for the cardinality (or measure ) of the set corresponding to such a region. For instance, the above Venn diagram can be used to intuitively justify the inclusion-exclusion formula

for finite sets , while the above Euler diagram similarly justifies the special case

for finite disjoint sets .

While Venn and Euler diagrams are traditionally two-dimensional in nature, there is nothing preventing one from using one-dimensional diagrams such as

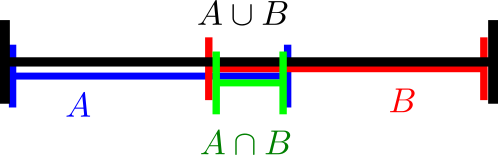
or even three-dimensional diagrams such as this one from Wikipedia:

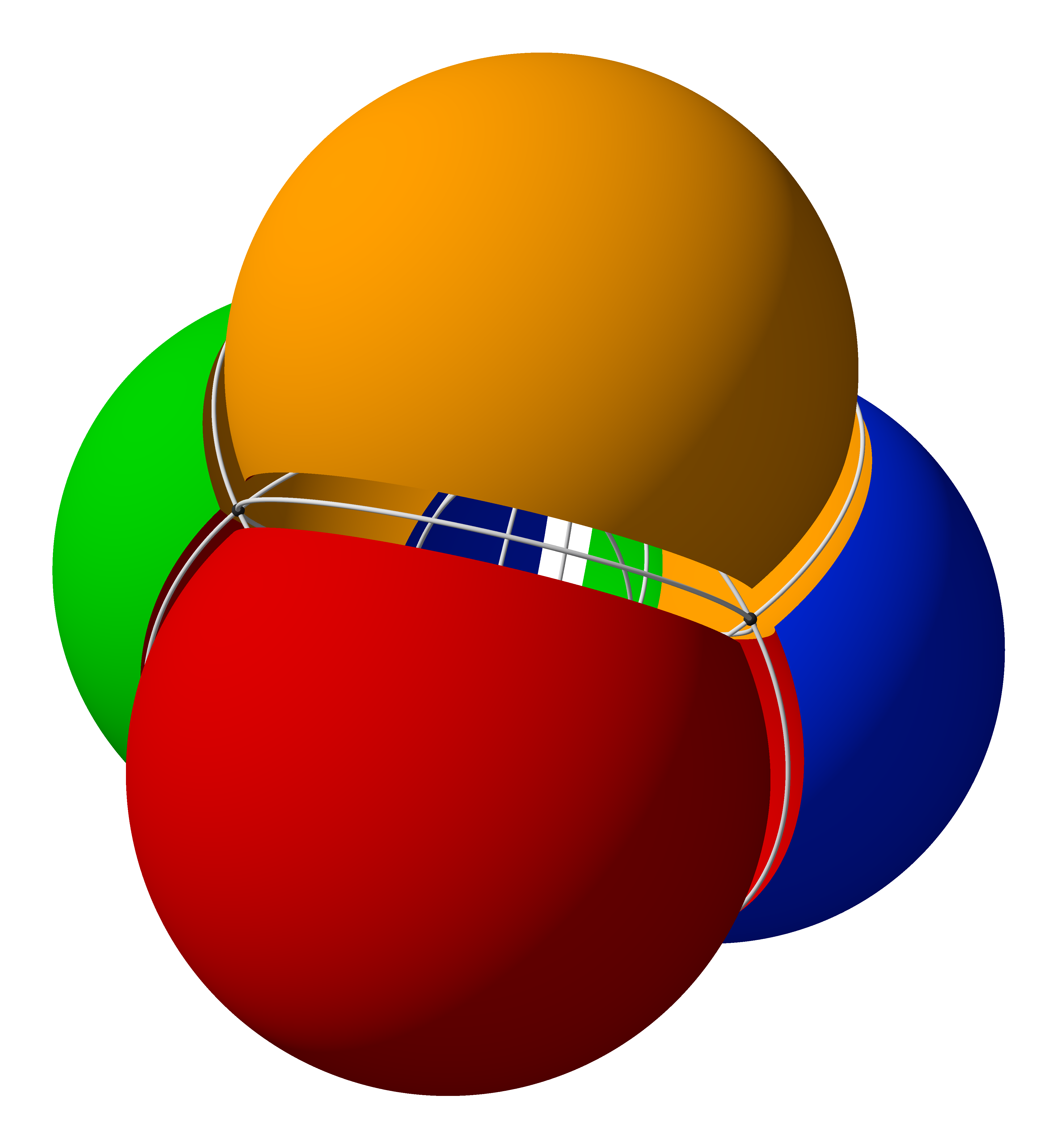
Of course, in such cases one would use length or volume as a heuristic proxy for cardinality or measure, rather than area.

With the addition of arrows, Venn and Euler diagrams can also accommodate (to some extent) functions between sets. Here for instance is a depiction of a function , the image of that function, and the image of some subset of :

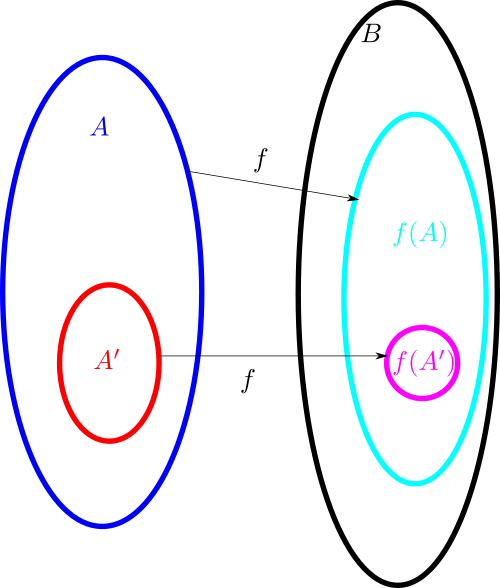
Here one can illustrate surjectivity of by having fill out all of ; one can similarly illustrate injectivity of by giving exactly the same shape (or at least the same area) as . So here for instance might be how one would illustrate an injective function :

Cartesian product operations can be incorporated into these diagrams by appropriate combinations of one-dimensional and two-dimensional diagrams. Here for instance is a diagram that illustrates the identity :

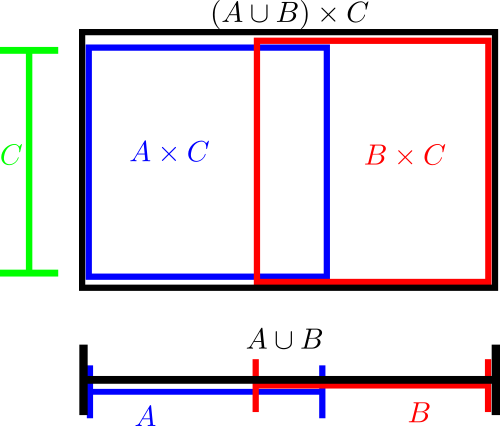
In this blog post I would like to propose a similar family of diagrams to illustrate relationships between vector spaces (over a fixed base field , such as the reals) or abelian groups, rather than sets. The categories of (-)vector spaces and abelian groups are quite similar in many ways; the former consists of modules over a base field , while the latter consists of modules over the integers ; also, both categories are basic examples of abelian categories. The notion of a dimension in a vector space is analogous in many ways to that of cardinality of a set; see this previous post for an instance of this analogy (in the context of Shannon entropy). (UPDATE: I have learned that an essentially identical notation has also been proposed in an unpublished manuscript of Ravi Vakil.)

Goursat and Furstenberg-Weiss type lemmas

I’m collecting in this blog post a number of simple group-theoretic lemmas, all of the following flavour: if is a subgroup of some product of groups, then one of three things has to happen:

• ( too small) is contained in some proper subgroup of , or the elements of are constrained to some sort of equation that the full group does not satisfy.
• ( too large) contains some non-trivial normal subgroup of , and as such actually arises by pullback from some subgroup of the quotient group .
• (Structure) There is some useful structural relationship between and the groups .

These sorts of lemmas show up often in ergodic theory, when the equidistribution of some orbit is governed by some unspecified subgroup of a product group , and one needs to know further information about this subgroup in order to take the analysis further. In some cases only two of the above three options are relevant. In the cases where is too “small” or too “large” one can reduce the groups to something smaller (either a subgroup or a quotient) and in applications one can often proceed in this case by some induction on the “size” of the groups (for instance, if these groups are Lie groups, one can often perform an induction on dimension), so it is often the structured case which is the most interesting case to deal with.

It is perhaps easiest to explain the flavour of these lemmas with some simple examples, starting with the case where we are just considering subgroups of a single group .

Lemma 1 Let be a subgroup of a group . Then exactly one of the following hold:

• (i) ( too small) There exists a non-trivial group homomorphism into a group such that for all .
• (ii) ( normally generates ) is generated as a group by the conjugates of .

Proof: Let be the group normally generated by , that is to say the group generated by the conjugates of . This is a normal subgroup of containing (indeed it is the smallest such normal subgroup). If is all of we are in option (ii); otherwise we can take to be the quotient group and to be the quotient map. Finally, if (i) holds, then all of the conjugates of lie in the kernel of , and so (ii) cannot hold.

Here is a “dual” to the above lemma:

Lemma 2 Let be a subgroup of a group . Then exactly one of the following hold:

• (i) ( too large) is the pullback of some subgroup of for some non-trivial normal subgroup of , where is the quotient map.
• (ii) ( is core-free) does not contain any non-trivial conjugacy class .

Proof: Let be the normal core of , that is to say the intersection of all the conjugates of . This is the largest normal subgroup of that is contained in . If is non-trivial, we can quotient it out and end up with option (i). If instead is trivial, then there is no non-trivial element that lies in the core, hence no non-trivial conjugacy class lies in and we are in option (ii). Finally, if (i) holds, then every conjugacy class of an element of is contained in and hence in , so (ii) cannot hold.

For subgroups of nilpotent groups, we have a nice dichotomy that detects properness of a subgroup through abelian representations:

Lemma 3 Let be a subgroup of a nilpotent group . Then exactly one of the following hold:

• (i) ( too small) There exists non-trivial group homomorphism into an abelian group such that for all .
• (ii) .

Informally: if is a variable ranging in a subgroup of a nilpotent group , then either is unconstrained (in the sense that it really ranges in all of ), or it obeys some abelian constraint .

Proof: By definition of nilpotency, the lower central series

eventually becomes trivial.

Since is a normal subgroup of , is also a subgroup of . Suppose first that is a proper subgroup of , then the quotient map is a non-trivial homomorphism to an abelian group that annihilates , and we are in option (i). Thus we may assume that , and thus

Note that modulo the normal group , commutes with , hence

and thus

We conclude that . One can continue this argument by induction to show that for every ; taking large enough we end up in option (ii). Finally, it is clear that (i) and (ii) cannot both hold.

Remark 4 When the group is locally compact and is closed, one can take the homomorphism in Lemma 3 to be continuous, and by using Pontryagin duality one can also take the target group to be the unit circle . Thus is now a character of . Similar considerations hold for some of the later lemmas in this post. Discrete versions of this above lemma, in which the group is replaced by some orbit of a polynomial map on a nilmanifold, were obtained by Leibman and are important in the equidistribution theory of nilmanifolds; see this paper of Ben Green and myself for further discussion.

Here is an analogue of Lemma 3 for special linear groups, due to Serre (IV-23):

Lemma 5 Let be a prime, and let be a closed subgroup of , where is the ring of -adic integers. Then exactly one of the following hold:

• (i) ( too small) There exists a proper subgroup of such that for all .
• (ii) .

Proof: It is a standard fact that the reduction of mod is , hence (i) and (ii) cannot both hold.

Suppose that (i) fails, then for every there exists such that , which we write as

We now claim inductively that for any and , there exists with ; taking limits as using the closed nature of will then place us in option (ii).

The case is already handled, so now suppose . If , we see from the case that we can write where and . Thus to establish the claim it suffices to do so under the additional hypothesis that .

First suppose that for some with . By the case, we can find of the form for some . Raising to the power and using and , we note that

giving the claim in this case.

Any matrix of trace zero with coefficients in is a linear combination of , , and is thus a sum of matrices that square to zero. Hence, if is of the form , then for some matrix of trace zero, and thus one can write (up to errors) as the finite product of matrices of the form with . By the previous arguments, such a matrix lies in up to errors, and hence does also. This completes the proof of the case.

Now suppose and the claim has already been proven for . Arguing as before, it suffices to close the induction under the additional hypothesis that , thus we may write . By induction hypothesis, we may find with . But then , and we are done.

We note a generalisation of Lemma 3 that involves two groups rather than just one:

Lemma 6 Let be a subgroup of a product of two nilpotent groups . Then exactly one of the following hold:

• (i) ( too small) There exists group homomorphisms , into an abelian group , with non-trivial, such that for all , where is the projection of to .
• (ii) for some subgroup of .

Proof: Consider the group . This is a subgroup of . If it is all of , then must be a Cartesian product and option (ii) holds. So suppose that this group is a proper subgroup of . Applying Lemma 3, we obtain a non-trivial group homomorphism into an abelian group such that whenever . For any in the projection of to , there is thus a unique quantity such that whenever . One easily checks that is a homomorphism, so we are in option (i).

Finally, it is clear that (i) and (ii) cannot both hold, since (i) places a non-trivial constraint on the second component of an element of for any fixed choice of .

We also note a similar variant of Lemma 5, which is Lemme 10 of this paper of Serre:

Lemma 7 Let be a prime, and let be a closed subgroup of . Then exactly one of the following hold:

• (i) ( too small) There exists a proper subgroup of such that for all .
• (ii) .

Proof: As in the proof of Lemma 5, (i) and (ii) cannot both hold. Suppose that (i) does not hold, then for any there exists such that . Similarly, there exists with . Taking commutators of and , we can find with . Continuing to take commutators with and extracting a limit (using compactness and the closed nature of ), we can find with . Thus, the closed subgroup of does not obey conclusion (i) of Lemma 5, and must therefore obey conclusion (ii); that is to say, contains . Similarly contains ; multiplying, we end up in conclusion (ii).

The most famous result of this type is of course the Goursat lemma, which we phrase here in a somewhat idiosyncratic manner to conform to the pattern of the other lemmas in this post:

Lemma 8 (Goursat lemma) Let be a subgroup of a product of two groups . Then one of the following hold:

• (i) ( too small) is contained in for some subgroups , of respectively, with either or (or both).
• (ii) ( too large) There exist normal subgroups of respectively, not both trivial, such that arises from a subgroup of , where is the quotient map.
• (iii) (Isomorphism) There is a group isomorphism such that is the graph of . In particular, and are isomorphic.

Here we almost have a trichotomy, because option (iii) is incompatible with both option (i) and option (ii). However, it is possible for options (i) and (ii) to simultaneously hold.

Proof: If either of the projections , from to the factor groups (thus and fail to be surjective, then we are in option (i). Thus we may assume that these maps are surjective.

Next, if either of the maps , fail to be injective, then at least one of the kernels , is non-trivial. We can then descend down to the quotient and end up in option (ii).

The only remaining case is when the group homomorphisms are both bijections, hence are group isomorphisms. If we set we end up in case (iii).

We can combine the Goursat lemma with Lemma 3 to obtain a variant:

Corollary 9 (Nilpotent Goursat lemma) Let be a subgroup of a product of two nilpotent groups . Then one of the following hold:

• (i) ( too small) There exists and a non-trivial group homomorphism such that for all .
• (ii) ( too large) There exist normal subgroups of respectively, not both trivial, such that arises from a subgroup of .
• (iii) (Isomorphism) There is a group isomorphism such that is the graph of . In particular, and are isomorphic.

Proof: If Lemma 8(i) holds, then by applying Lemma 3 we arrive at our current option (i). The other options are unchanged from Lemma 8, giving the claim.

Now we present a lemma involving three groups that is known in ergodic theory contexts as the “Furstenberg-Weiss argument”, as an argument of this type arose in this paper of Furstenberg and Weiss, though perhaps it also implicitly appears in other contexts also. It has the remarkable feature of being able to enforce the abelian nature of one of the groups once the other options of the lemma are excluded.

Lemma 10 (Furstenberg-Weiss lemma) Let be a subgroup of a product of three groups . Then one of the following hold:

• (i) ( too small) There is some proper subgroup of and some such that whenever and .
• (ii) ( too large) There exists a non-trivial normal subgroup of with abelian, such that arises from a subgroup of , where is the quotient map.
• (iii) is abelian.

Proof: If the group is a proper subgroup of , then we are in option (i) (with ), so we may assume that

Similarly we may assume that

Now let be any two elements of . By the above assumptions, we can find such that

and

Taking commutators to eliminate the terms, we conclude that

Thus the group contains every commutator , and thus contains the entire group generated by these commutators. If fails to be abelian, then is a non-trivial normal subgroup of , and now arises from in the obvious fashion, placing one in option (ii). Hence the only remaining case is when is abelian, giving us option (iii).

As before, we can combine this with previous lemmas to obtain a variant in the nilpotent case:

Lemma 11 (Nilpotent Furstenberg-Weiss lemma) Let be a subgroup of a product of three nilpotent groups . Then one of the following hold:

• (i) ( too small) There exists and group homomorphisms , for some abelian group , with non-trivial, such that whenever , where is the projection of to .
• (ii) ( too large) There exists a non-trivial normal subgroup of , such that arises from a subgroup of .
• (iii) is abelian.

Informally, this lemma asserts that if is a variable ranging in some subgroup , then either (i) there is a non-trivial abelian equation that constrains in terms of either or ; (ii) is not fully determined by and ; or (iii) is abelian.

Proof: Applying Lemma 10, we are already done if conclusions (ii) or (iii) of that lemma hold, so suppose instead that conclusion (i) holds for say . Then the group is not of the form , since it only contains those with . Applying Lemma 6, we obtain group homomorphisms , into an abelian group , with non-trivial, such that whenever , placing us in option (i).

The Furstenberg-Weiss argument is often used (though not precisely in this form) to establish that certain key structure groups arising in ergodic theory are abelian; see for instance Proposition 6.3(1) of this paper of Host and Kra for an example.

One can get more structural control on in the Furstenberg-Weiss lemma in option (iii) if one also broadens options (i) and (ii):

Lemma 12 (Variant of Furstenberg-Weiss lemma) Let be a subgroup of a product of three groups . Then one of the following hold:

• (i) ( too small) There is some proper subgroup of for some such that whenever . (In other words, the projection of to is not surjective.)
• (ii) ( too large) There exists a normal of respectively, not all trivial, such that arises from a subgroup of , where is the quotient map.
• (iii) are abelian and isomorphic. Furthermore, there exist isomorphisms , , to an abelian group such that

  

The ability to encode an abelian additive relation in terms of group-theoretic properties is vaguely reminiscent of the group configuration theorem.

Proof: We apply Lemma 10. Option (i) of that lemma implies option (i) of the current lemma, and similarly for option (ii), so we may assume without loss of generality that is abelian. By permuting we may also assume that are abelian, and will use additive notation for these groups.

We may assume that the projections of to and are surjective, else we are in option (i). The group is then a normal subgroup of ; we may assume it is trivial, otherwise we can quotient it out and be in option (ii). Thus can be expressed as a graph for some map . As is a group, must be a homomorphism, and we can write it as for some homomorphisms , . Thus elements of obey the constraint .

If or fails to be injective, then we can quotient out by their kernels and end up in option (ii). If fails to be surjective, then the projection of to also fails to be surjective (since for , is now constrained to lie in the range of ) and we are in option (i). Similarly if fails to be surjective. Thus we may assume that the homomorphisms are bijective and thus group isomorphisms. Setting to the identity, we arrive at option (iii).

Combining this lemma with Lemma 3, we obtain a nilpotent version:

Corollary 13 (Variant of nilpotent Furstenberg-Weiss lemma) Let be a subgroup of a product of three groups . Then one of the following hold:

• (i) ( too small) There are homomorphisms , to some abelian group for some , with not both trivial, such that whenever .
• (ii) ( too large) There exists a normal of respectively, not all trivial, such that arises from a subgroup of , where is the quotient map.
• (iii) are abelian and isomorphic. Furthermore, there exist isomorphisms , , to an abelian group such that

  

Here is another variant of the Furstenberg-Weiss lemma, attributed to Serre by Ribet (see Lemma 3.3):

Lemma 14 (Serre’s lemma) Let be a subgroup of a finite product of groups with . Then one of the following hold:

• (i) ( too small) There is some proper subgroup of for some such that whenever .
• (ii) ( too large) One has .
• (iii) One of the has a non-trivial abelian quotient .

Proof: The claim is trivial for (and we don’t need (iii) in this case), so suppose that . We can assume that each is a perfect group, , otherwise we can quotient out by the commutator and arrive in option (iii). Similarly, we may assume that all the projections of to , are surjective, otherwise we are in option (i).

We now claim that for any and any , one can find with for and . For this follows from the surjectivity of the projection of to . Now suppose inductively that and the claim has already been proven for . Since is perfect, it suffices to establish this claim for of the form for some . By induction hypothesis, we can find with for and . By surjectivity of the projection of to , one can find with and . Taking commutators of these two elements, we obtain the claim.

Setting , we conclude that contains . Similarly for permutations. Multiplying these together we see that contains all of , and we are in option (ii).

The alternative hypothesis for unitary matrices

In a recent post I discussed how the Riemann zeta function can be locally approximated by a polynomial, in the sense that for randomly chosen one has an approximation

where grows slowly with , and is a polynomial of degree . Assuming the Riemann hypothesis (as we will throughout this post), the zeroes of should all lie on the unit circle, and one should then be able to write as a scalar multiple of the characteristic polynomial of (the inverse of) a unitary matrix , which we normalise as

Here is some quantity depending on . We view as a random element of ; in the limit , the GUE hypothesis is equivalent to becoming equidistributed with respect to Haar measure on (also known as the Circular Unitary Ensemble, CUE; it is to the unit circle what the Gaussian Unitary Ensemble (GUE) is on the real line). One can also view as analogous to the “geometric Frobenius” operator in the function field setting, though unfortunately it is difficult at present to make this analogy any more precise (due, among other things, to the lack of a sufficiently satisfactory theory of the “field of one element“).

Taking logarithmic derivatives of (2), we have

and hence on taking logarithmic derivatives of (1) in the variable we (heuristically) have

Morally speaking, we have

so on comparing coefficients we expect to interpret the moments of as a finite Dirichlet series:

To understand the distribution of in the unitary group , it suffices to understand the distribution of the moments

where denotes averaging over , and . The GUE hypothesis asserts that in the limit , these moments converge to their CUE counterparts

where is now drawn uniformly in with respect to the CUE ensemble, and denotes expectation with respect to that measure.

The moment (6) vanishes unless one has the homogeneity condition

This follows from the fact that for any phase , has the same distribution as , where we use the number theory notation .

In the case when the degree is low, we can use representation theory to establish the following simple formula for the moment (6), as evaluated by Diaconis and Shahshahani:

Proposition 1 (Low moments in CUE model) If

then the moment (6) vanishes unless for all , in which case it is equal to

Another way of viewing this proposition is that for distributed according to CUE, the random variables are distributed like independent complex random variables of mean zero and variance , as long as one only considers moments obeying (8). This identity definitely breaks down for larger values of , so one only obtains central limit theorems in certain limiting regimes, notably when one only considers a fixed number of ‘s and lets go to infinity. (The paper of Diaconis and Shahshahani writes in place of , but I believe this to be a typo.)

Proof: Let be the left-hand side of (8). We may assume that (7) holds since we are done otherwise, hence

Our starting point is Schur-Weyl duality. Namely, we consider the -dimensional complex vector space

This space has an action of the product group : the symmetric group acts by permutation on the tensor factors, while the general linear group acts diagonally on the factors, and the two actions commute with each other. Schur-Weyl duality gives a decomposition

where ranges over Young tableaux of size with at most rows, is the -irreducible unitary representation corresponding to (which can be constructed for instance using Specht modules), and is the -irreducible polynomial representation corresponding with highest weight .

Let be a permutation consisting of cycles of length (this is uniquely determined up to conjugation), and let . The pair then acts on , with the action on basis elements given by

The trace of this action can then be computed as

where is the matrix coefficient of . Breaking up into cycles and summing, this is just

But we can also compute this trace using the Schur-Weyl decomposition (10), yielding the identity

where is the character on associated to , and is the character on associated to . As is well known, is just the Schur polynomial of weight applied to the (algebraic, generalised) eigenvalues of . We can specialise to unitary matrices to conclude that

and similarly

where consists of cycles of length for each . On the other hand, the characters are an orthonormal system on with the CUE measure. Thus we can write the expectation (6) as

Now recall that ranges over all the Young tableaux of size with at most rows. But by (8) we have , and so the condition of having rows is redundant. Hence now ranges over all Young tableaux of size , which as is well known enumerates all the irreducible representations of . One can then use the standard orthogonality properties of characters to show that the sum (12) vanishes if , are not conjugate, and is equal to divided by the size of the conjugacy class of (or equivalently, by the size of the centraliser of ) otherwise. But the latter expression is easily computed to be , giving the claim.

Example 2 We illustrate the identity (11) when , . The Schur polynomials are given as

where are the (generalised) eigenvalues of , and the formula (11) in this case becomes

The functions are orthonormal on , so the three functions are also, and their norms are , , and respectively, reflecting the size in of the centralisers of the permutations , , and respectively. If is instead set to say , then the terms now disappear (the Young tableau here has too many rows), and the three quantities here now have some non-trivial covariance.

Example 3 Consider the moment . For , the above proposition shows us that this moment is equal to . What happens for ? The formula (12) computes this moment as

where is a cycle of length in , and ranges over all Young tableaux with size and at most rows. The Murnaghan-Nakayama rule tells us that vanishes unless is a hook (all but one of the non-zero rows consisting of just a single box; this also can be interpreted as an exterior power representation on the space of vectors in whose coordinates sum to zero), in which case it is equal to (depending on the parity of the number of non-zero rows). As such we see that this moment is equal to . Thus in general we have

Now we discuss what is known for the analogous moments (5). Here we shall be rather non-rigorous, in particular ignoring an annoying “Archimedean” issue that the product of the ranges and is not quite the range but instead leaks into the adjacent range . This issue can be addressed by working in a “weak" sense in which parameters such as are averaged over fairly long scales, or by passing to a function field analogue of these questions, but we shall simply ignore the issue completely and work at a heuristic level only. For similar reasons we will ignore some technical issues arising from the sharp cutoff of to the range (it would be slightly better technically to use a smooth cutoff).

One can morally expand out (5) using (4) as

where , , and the integers are in the ranges

for and , and

for and . Morally, the expectation here is negligible unless

in which case the expecation is oscillates with magnitude one. In particular, if (7) fails (with some room to spare) then the moment (5) should be negligible, which is consistent with the analogous behaviour for the moments (6). Now suppose that (8) holds (with some room to spare). Then is significantly less than , so the multiplicative error in (15) becomes an additive error of . On the other hand, because of the fundamental integrality gap – that the integers are always separated from each other by a distance of at least – this forces the integers , to in fact be equal:

The von Mangoldt factors effectively restrict to be prime (the effect of prime powers is negligible). By the fundamental theorem of arithmetic, the constraint (16) then forces , and to be a permutation of , which then forces for all ._ For a given , the number of possible is then , and the expectation in (14) is equal to . Thus this expectation is morally

and using Mertens’ theorem this soon simplifies asymptotically to the same quantity in Proposition 1. Thus we see that (morally at least) the moments (5) associated to the zeta function asymptotically match the moments (6) coming from the CUE model in the low degree case (8), thus lending support to the GUE hypothesis. (These observations are basically due to Rudnick and Sarnak, with the degree case of pair correlations due to Montgomery, and the degree case due to Hejhal.)

With some rare exceptions (such as those estimates coming from “Kloostermania”), the moment estimates of Rudnick and Sarnak basically represent the state of the art for what is known for the moments (5). For instance, Montgomery’s pair correlation conjecture, in our language, is basically the analogue of (13) for , thus

for all . Montgomery showed this for (essentially) the range (as remarked above, this is a special case of the Rudnick-Sarnak result), but no further cases of this conjecture are known.

These estimates can be used to give some non-trivial information on the largest and smallest spacings between zeroes of the zeta function, which in our notation corresponds to spacing between eigenvalues of . One such method used today for this is due to Montgomery and Odlyzko and was greatly simplified by Conrey, Ghosh, and Gonek. The basic idea, translated to our random matrix notation, is as follows. Suppose is some random polynomial depending on of degree at most . Let denote the eigenvalues of , and let be a parameter. Observe from the pigeonhole principle that if the quantity

exceeds the quantity

then the arcs cannot all be disjoint, and hence there exists a pair of eigenvalues making an angle of less than ( times the mean angle separation). Similarly, if the quantity (18) falls below that of (19), then these arcs cannot cover the unit circle, and hence there exists a pair of eigenvalues making an angle of greater than times the mean angle separation. By judiciously choosing the coefficients of as functions of the moments , one can ensure that both quantities (18), (19) can be computed by the Rudnick-Sarnak estimates (or estimates of equivalent strength); indeed, from the residue theorem one can write (18) as

for sufficiently small , and this can be computed (in principle, at least) using (3) if the coefficients of are in an appropriate form. Using this sort of technology (translated back to the Riemann zeta function setting), one can show that gaps between consecutive zeroes of zeta are less than times the mean spacing and greater than times the mean spacing infinitely often for certain ; the current records are (due to Goldston and Turnage-Butterbaugh) and (due to Bui and Milinovich, who input some additional estimates beyond the Rudnick-Sarnak set, namely the twisted fourth moment estimates of Bettin, Bui, Li, and Radziwill, and using a technique based on Hall’s method rather than the Montgomery-Odlyzko method).

It would be of great interest if one could push the upper bound for the smallest gap below . The reason for this is that this would then exclude the Alternative Hypothesis that the spacing between zeroes are asymptotically always (or almost always) a non-zero half-integer multiple of the mean spacing, or in our language that the gaps between the phases of the eigenvalues of are nasymptotically always non-zero integer multiples of . The significance of this hypothesis is that it is implied by the existence of a Siegel zero (of conductor a small power of ); see this paper of Conrey and Iwaniec. (In our language, what is going on is that if there is a Siegel zero in which is very close to zero, then behaves like the Kronecker delta, and hence (by the Riemann-Siegel formula) the combined -function will have a polynomial approximation which in our language looks like a scalar multiple of , where and is a phase. The zeroes of this approximation lie on a coset of the roots of unity; the polynomial is a factor of this approximation and hence will also lie in this coset, implying in particular that all eigenvalue spacings are multiples of . Taking then gives the claim.)

Unfortunately, the known methods do not seem to break this barrier without some significant new input; already the original paper of Montgomery and Odlyzko observed this limitation for their particular technique (and in fact fall very slightly short, as observed in unpublished work of Goldston and of Milinovich). In this post I would like to record another way to see this, by providing an “alternative” probability distribution to the CUE distribution (which one might dub the Alternative Circular Unitary Ensemble (ACUE) which is indistinguishable in low moments in the sense that the expectation for this model also obeys Proposition 1, but for which the phase spacings are always a multiple of . This shows that if one is to rule out the Alternative Hypothesis (and thus in particular rule out Siegel zeroes), one needs to input some additional moment information beyond Proposition 1. It would be interesting to see if any of the other known moment estimates that go beyond this proposition are consistent with this alternative distribution. (UPDATE: it looks like they are, see Remark 7 below.)

To describe this alternative distribution, let us first recall the Weyl description of the CUE measure on the unitary group in terms of the distribution of the phases of the eigenvalues, randomly permuted in any order. This distribution is given by the probability measure

where

is the Vandermonde determinant; see for instance this previous blog post for the derivation of a very similar formula for the GUE distribution, which can be adapted to CUE without much difficulty. To see that this is a probability measure, first observe the Vandermonde determinant identity

where , denotes the dot product, and is the “long word”, which implies that (20) is a trigonometric series with constant term ; it is also clearly non-negative, so it is a probability measure. One can thus generate a random CUE matrix by first drawing using the probability measure (20), and then generating to be a random unitary matrix with eigenvalues .

For the alternative distribution, we first draw on the discrete torus (thus each is a root of unity) with probability density function

shift by a phase drawn uniformly at random, and then select to be a random unitary matrix with eigenvalues . Let us first verify that (21) is a probability density function. Clearly it is non-negative. It is the linear combination of exponentials of the form for . The diagonal contribution gives the constant function , which has total mass one. All of the other exponentials have a frequency that is not a multiple of , and hence will have mean zero on . The claim follows.

From construction it is clear that the matrix drawn from this alternative distribution will have all eigenvalue phase spacings be a non-zero multiple of . Now we verify that the alternative distribution also obeys Proposition 1. The alternative distribution remains invariant under rotation by phases, so the claim is again clear when (8) fails. Inspecting the proof of that proposition, we see that it suffices to show that the Schur polynomials with of size at most and of equal size remain orthonormal with respect to the alternative measure. That is to say,

when have size equal to each other and at most . In this case the phase in the definition of is irrelevant. In terms of eigenvalue measures, we are then reduced to showing that

By Fourier decomposition, it then suffices to show that the trigonometric polynomial does not contain any components of the form for some non-zero lattice vector . But we have already observed that is a linear combination of plane waves of the form for . Also, as is well known, is a linear combination of plane waves where is majorised by , and similarly is a linear combination of plane waves where is majorised by . So the product is a linear combination of plane waves of the form . But every coefficient of the vector lies between and , and so cannot be of the form for any non-zero lattice vector , giving the claim.

Example 4 If , then the distribution (21) assigns a probability of to any pair that is a permuted rotation of , and a probability of to any pair that is a permuted rotation of . Thus, a matrix drawn from the alternative distribution will be conjugate to a phase rotation of with probability , and to with probability .

A similar computation when gives conjugate to a phase rotation of with probability , to a phase rotation of or its adjoint with probability of each, and a phase rotation of with probability .

Remark 5 For large it does not seem that this specific alternative distribution is the only distribution consistent with Proposition 1 and which has all phase spacings a non-zero multiple of ; in particular, it may not be the only distribution consistent with a Siegel zero. Still, it is a very explicit distribution that might serve as a test case for the limitations of various arguments for controlling quantities such as the largest or smallest spacing between zeroes of zeta. The ACUE is in some sense the distribution that maximally resembles CUE (in the sense that it has the greatest number of Fourier coefficients agreeing) while still also being consistent with the Alternative Hypothesis, and so should be the most difficult enemy to eliminate if one wishes to disprove that hypothesis.

In some cases, even just a tiny improvement in known results would be able to exclude the alternative hypothesis. For instance, if the alternative hypothesis held, then is periodic in with period , so from Proposition 1 for the alternative distribution one has

which differs from (13) for any . (This fact was implicitly observed recently by Baluyot, in the original context of the zeta function.) Thus a verification of the pair correlation conjecture (17) for even a single with would rule out the alternative hypothesis. Unfortunately, such a verification appears to be on comparable difficulty with (an averaged version of) the Hardy-Littlewood conjecture, with power saving error term. (This is consistent with the fact that Siegel zeroes can cause distortions in the Hardy-Littlewood conjecture, as (implicitly) discussed in this previous blog post.)

Remark 6 One can view the CUE as normalised Lebesgue measure on (viewed as a smooth submanifold of ). One can similarly view ACUE as normalised Lebesgue measure on the (disconnected) smooth submanifold of consisting of those unitary matrices whose phase spacings are non-zero integer multiples of ; informally, ACUE is CUE restricted to this lower dimensional submanifold. As is well known, the phases of CUE eigenvalues form a determinantal point process with kernel (or one can equivalently take ; in a similar spirit, the phases of ACUE eigenvalues, once they are rotated to be roots of unity, become a discrete determinantal point process on those roots of unity with exactly the same kernel (except for a normalising factor of ). In particular, the -point correlation functions of ACUE (after this rotation) are precisely the restriction of the -point correlation functions of CUE after normalisation, that is to say they are proportional to .

Remark 7 One family of estimates that go beyond the Rudnick-Sarnak family of estimates are twisted moment estimates for the zeta function, such as ones that give asymptotics for

for some small even exponent (almost always or ) and some short Dirichlet polynomial ; see for instance this paper of Bettin, Bui, Li, and Radziwill for some examples of such estimates. The analogous unitary matrix average would be something like

where is now some random medium degree polynomial that depends on the unitary matrix associated to (and in applications will typically also contain some negative power of to cancel the corresponding powers of in ). Unfortunately such averages generally are unable to distinguish the CUE from the ACUE. For instance, if all the coefficients of involve products of traces of total order less than , then in terms of the eigenvalue phases , is a linear combination of plane waves where the frequencies have coefficients of magnitude less than . On the other hand, as each coefficient of is an elementary symmetric function of the eigenvalues, is a linear combination of plane waves where the frequencies have coefficients of magnitude at most . Thus is a linear combination of plane waves where the frequencies have coefficients of magnitude less than , and thus is orthogonal to the difference between the CUE and ACUE measures on the phase torus by the previous arguments. In other words, has the same expectation with respect to ACUE as it does with respect to CUE. Thus one can only start distinguishing CUE from ACUE if the mollifier has degree close to or exceeding , which corresponds to Dirichlet polynomials of length close to or exceeding , which is far beyond current technology for such moment estimates.

Remark 8 The GUE hypothesis for the zeta function asserts that the average

is equal to

for any and any test function , where is the Dyson sine kernel and are the ordinates of zeroes of the zeta function. This corresponds to the CUE distribution for . The ACUE distribution then corresponds to an “alternative gaussian unitary ensemble (AGUE)” hypothesis, in which the average (22) is instead predicted to equal a Riemann sum version of the integral (23):

This is a stronger version of the alternative hypothesis that the spacing between adjacent zeroes is almost always approximately a half-integer multiple of the mean spacing. I do not know of any known moment estimates for Dirichlet series that is able to eliminate this AGUE hypothesis (even assuming GRH). (UPDATE: These facts have also been independently observed in forthcoming work of Lagarias and Rodgers.)

1% quasimorphisms and group cohomology

Let , be additive groups (i.e., groups with an abelian addition group law). A map is a homomorphism if one has

for all . A map is an affine homomorphism if one has

for all additive quadruples in , by which we mean that and . The two notions are closely related; it is easy to verify that is an affine homomorphism if and only if is the sum of a homomorphism and a constant.

Now suppose that also has a translation-invariant metric . A map is said to be a quasimorphism if one has

for all , where denotes a quantity at a bounded distance from the origin. Similarly, is an affine quasimorphism if

for all additive quadruples in . Again, one can check that is an affine quasimorphism if and only if it is the sum of a quasimorphism and a constant (with the implied constant of the quasimorphism controlled by the implied constant of the affine quasimorphism). (Since every constant is itself a quasimorphism, it is in fact the case that affine quasimorphisms are quasimorphisms, but now the implied constant in the latter is not controlled by the implied constant of the former.)

“Trivial” examples of quasimorphisms include the sum of a homomorphism and a bounded function. Are there others? In some cases, the answer is no. For instance, suppose we have a quasimorphism . Iterating (2), we see that for any integer and natural number , which we can rewrite as for non-zero . Also, is Lipschitz. Sending , we can verify that is a Cauchy sequence as and thus tends to some limit ; we have for , hence for positive , and then one can use (2) one last time to obtain for all . Thus is the sum of the homomorphism and a bounded sequence.

In general, one can phrase this problem in the language of group cohomology (discussed in this previous post). Call a map a -cocycle. A -cocycle is a map obeying the identity

for all . Given a -cocycle , one can form its derivative by the formula

Such functions are called -coboundaries. It is easy to see that the abelian group of -coboundaries is a subgroup of the abelian group of -cocycles. The quotient of these two groups is the first group cohomology of with coefficients in , and is denoted .

If a -cocycle is bounded then its derivative is a bounded -coboundary. The quotient of the group of bounded -cocycles by the derivatives of bounded -cocycles is called the bounded first group cohomology of with coefficients in , and is denoted . There is an obvious homomorphism from to , formed by taking a coset of the space of derivatives of bounded -cocycles, and enlarging it to a coset of the space of -coboundaries. By chasing all the definitions, we see that all quasimorphism from to are the sum of a homomorphism and a bounded function if and only if this homomorphism is injective; in fact the quotient of the space of quasimorphisms by the sum of homomorphisms and bounded functions is isomorphic to the kernel of .

In additive combinatorics, one is often working with functions which only have additive structure a fraction of the time, thus for instance (1) or (3) might only hold “ of the time”. This makes it somewhat difficult to directly interpret the situation in terms of group cohomology. However, thanks to tools such as the Balog-Szemerédi-Gowers lemma, one can upgrade this sort of -structure to -structure – at the cost of restricting the domain to a smaller set. Here I record one such instance of this phenomenon, thus giving a tentative link between additive combinatorics and group cohomology. (I thank Yuval Wigderson for suggesting the problem of locating such a link.)

Theorem 1 Let , be additive groups with , let be a subset of , let , and let be a function such that

for additive quadruples in . Then there exists a subset of containing with , a subset of with , and a function such that

for all (thus, the derivative takes values in on ), and such that for each , one has

for values of .

Presumably the constants and can be improved further, but we have not attempted to optimise these constants. We chose as the domain on which one has a bounded derivative, as one can use the Bogulybov lemma (see e.g, Proposition 4.39 of my book with Van Vu) to find a large Bohr set inside . In applications, the set need not have bounded size, or even bounded doubling; for instance, in the inverse theory over a small finite fields , one would be interested in the situation where is the group of matrices with coefficients in (for some large , and being the subset consisting of those matrices of rank bounded by some bound .

Proof: By hypothesis, there are triples such that and

Thus, there is a set with such that for all , one has (6) for pairs with ; in particular, there exists such that (6) holds for values of . Setting , we conclude that for each , one has

for values of .

Consider the bipartite graph whose vertex sets are two copies of , and and connected by a (directed) edge if and (7) holds. Then this graph has edges. Applying (a slight modification of) the Balog-Szemerédi-Gowers theorem (for instance by modifying the proof of Corollary 5.19 of my book with Van Vu), we can then find a subset of with with the property that for any , there exist triples such that the edges all lie in this bipartite graph. This implies that, for all , there exist septuples obeying the constraints

and for . These constraints imply in particular that

Also observe that

Thus, if and are such that , we see that

for octuples in the hyperplane

By the pigeonhole principle, this implies that for any fixed , there can be at most sets of the form with , that are pairwise disjoint. Using a greedy algorithm, we conclude that there is a set of cardinality , such that each set with , intersects for some , or in other words that

whenever . In particular,

This implies that there exists a subset of with , and an element for each , such that

for all . Note we may assume without loss of generality that and .

Suppose that are such that

By construction of , and permuting labels, we can find 16-tuples such that

and

for . We sum this to obtain

and hence by (8)

where . Since

we see that there are only possible values of . By the pigeonhole principle, we conclude that at most of the sets can be disjoint. Arguing as before, we conclude that there exists a set of cardinality such that

whenever (10) holds.

For any , write arbitrarily as for some (with if , and if ) and then set

Then from (11) we have (4). For we have , and (5) then follows from (9).

Heat flow and zeroes of polynomials II: zeroes on a circle

This is a sequel to this previous blog post, in which we discussed the effect of the heat flow evolution

on the zeroes of a time-dependent family of polynomials , with a particular focus on the case when the polynomials had real zeroes. Here (inspired by some discussions I had during a recent conference on the Riemann hypothesis in Bristol) we record the analogous theory in which the polynomials instead have zeroes on a circle , with the heat flow slightly adjusted to compensate for this. As we shall discuss shortly, a key example of this situation arises when is the numerator of the zeta function of a curve.

More precisely, let be a natural number. We will say that a polynomial

of degree (so that ) obeys the functional equation if the are all real and

for all , thus

and

for all non-zero . This means that the zeroes of (counting multiplicity) lie in and are symmetric with respect to complex conjugation and inversion across the circle . We say that this polynomial obeys the Riemann hypothesis if all of its zeroes actually lie on the circle . For instance, in the case, the polynomial obeys the Riemann hypothesis if and only if .

Such polynomials arise in number theory as follows: if is a projective curve of genus over a finite field , then, as famously proven by Weil, the associated local zeta function (as defined for instance in this previous blog post) is known to take the form

where is a degree polynomial obeying both the functional equation and the Riemann hypothesis. In the case that is an elliptic curve, then and takes the form , where is the number of -points of minus . The Riemann hypothesis in this case is a famous result of Hasse.

Another key example of such polynomials arise from rescaled characteristic polynomials

of matrices in the compact symplectic group . These polynomials obey both the functional equation and the Riemann hypothesis. The Sato-Tate conjecture (in higher genus) asserts, roughly speaking, that “typical” polyomials arising from the number theoretic situation above are distributed like the rescaled characteristic polynomials (1), where is drawn uniformly from with Haar measure.

Given a polynomial of degree with coefficients

we can evolve it in time by the formula

thus for . Informally, as one increases , this evolution accentuates the effect of the extreme monomials, particularly, and at the expense of the intermediate monomials such as , and conversely as one decreases . This family of polynomials obeys the heat-type equation

In view of the results of Marcus, Spielman, and Srivastava, it is also very likely that one can interpret this flow in terms of expected characteristic polynomials involving conjugation over the compact symplectic group , and should also be tied to some sort of “” version of Brownian motion on this group, but we have not attempted to work this connection out in detail.

It is clear that if obeys the functional equation, then so does for any other time . Now we investigate the evolution of the zeroes. Suppose at some time that the zeroes of are distinct, then

From the inverse function theorem we see that for times sufficiently close to , the zeroes of continue to be distinct (and vary smoothly in ), with

Differentiating this at any not equal to any of the , we obtain

and

and

Inserting these formulae into (2) (expanding as ) and canceling some terms, we conclude that

for sufficiently close to , and not equal to . Extracting the residue at , we conclude that

which we can rearrange as

If we make the change of variables (noting that one can make depend smoothly on for sufficiently close to ), this becomes

Intuitively, this equation asserts that the phases repel each other if they are real (and attract each other if their difference is imaginary). If obeys the Riemann hypothesis, then the are all real at time , then the Picard uniqueness theorem (applied to and its complex conjugate) then shows that the are also real for sufficiently close to . If we then define the entropy functional

then the above equation becomes a gradient flow

which implies in particular that is non-increasing in time. This shows that as one evolves time forward from , there is a uniform lower bound on the separation between the phases , and hence the equation can be solved indefinitely; in particular, obeys the Riemann hypothesis for all if it does so at time . Our argument here assumed that the zeroes of were simple, but this assumption can be removed by the usual limiting argument.

For any polynomial obeying the functional equation, the rescaled polynomials converge locally uniformly to as . By Rouche’s theorem, we conclude that the zeroes of converge to the equally spaced points on the circle . Together with the symmetry properties of the zeroes, this implies in particular that obeys the Riemann hypothesis for all sufficiently large positive . In the opposite direction, when , the polynomials converge locally uniformly to , so if , of the zeroes converge to the origin and the other converge to infinity. In particular, fails the Riemann hypothesis for sufficiently large negative . Thus (if ), there must exist a real number , which we call the de Bruijn-Newman constant of the original polynomial , such that obeys the Riemann hypothesis for and fails the Riemann hypothesis for . The situation is a bit more complicated if vanishes; if is the first natural number such that (or equivalently, ) does not vanish, then by the above arguments one finds in the limit that of the zeroes go to the origin, go to infinity, and the remaining zeroes converge to the equally spaced points . In this case the de Bruijn-Newman constant remains finite except in the degenerate case , in which case .

For instance, consider the case when and for some real with . Then the quadratic polynomial

has zeroes

and one easily checks that these zeroes lie on the circle when , and are on the real axis otherwise. Thus in this case we have (with if ). Note how as increases to , the zeroes repel each other and eventually converge to , while as decreases to , the zeroes collide and then separate on the real axis, with one zero going to the origin and the other to infinity.

The arguments in my paper with Brad Rodgers (discussed in this previous post) indicate that for a “typical” polynomial of degree that obeys the Riemann hypothesis, the expected time to relaxation to equilibrium (in which the zeroes are equally spaced) should be comparable to , basically because the average spacing is and hence by (3) the typical velocity of the zeroes should be comparable to , and the diameter of the unit circle is comparable to , thus requiring time comparable to to reach equilibrium. Taking contrapositives, this suggests that the de Bruijn-Newman constant should typically take on values comparable to (since typically one would not expect the initial configuration of zeroes to be close to evenly spaced). I have not attempted to formalise or prove this claim, but presumably one could do some numerics (perhaps using some of the examples of given previously) to explore this further.

Homogeneous length functions on groups

The Polymath14 online collaboration has uploaded to the arXiv its paper “Homogeneous length functions on groups“, submitted to Algebra & Number Theory. The paper completely classifies homogeneous length functions on an arbitrary group , that is to say non-negative functions that obey the symmetry condition , the non-degeneracy condition , the triangle inequality , and the homogeneity condition . It turns out that these norms can only arise from pulling back the norm of a Banach space by an isometric embedding of the group. Among other things, this shows that can only support a homogeneous length function if and only if it is abelian and torsion free, thus giving a metric description of this property.

The proof is based on repeated use of the homogeneous length function axioms, combined with elementary identities of commutators, to obtain increasingly good bounds on quantities such as , until one can show that such norms have to vanish. See the previous post for a full proof. The result is robust in that it allows for some loss in the triangle inequality and homogeneity condition, allowing for some new results on “quasinorms” on groups that relate to quasihomomorphisms.

As there are now a large number of comments on the previous post on this project, this post will also serve as the new thread for any final discussion of this project as it winds down.

Metrics of linear growth – the solution

In the tradition of “Polymath projects“, the problem posed in the previous two blog posts has now been solved, thanks to the cumulative effect of many small contributions by many participants (including, but not limited to, Sean Eberhard, Tobias Fritz, Siddharta Gadgil, Tobias Hartnick, Chris Jerdonek, Apoorva Khare, Antonio Machiavelo, Pace Nielsen, Andy Putman, Will Sawin, Alexander Shamov, Lior Silberman, and David Speyer). In this post I’ll write down a streamlined resolution, eliding a number of important but ultimately removable partial steps and insights made by the above contributors en route to the solution.

Theorem 1 Let be a group. Suppose one has a “seminorm” function which obeys the triangle inequality

for all , with equality whenever . Then the seminorm factors through the abelianisation map .

Proof: By the triangle inequality, it suffices to show that for all , where is the commutator.

We first establish some basic facts. Firstly, by hypothesis we have , and hence whenever is a power of two. On the other hand, by the triangle inequality we have for all positive , and hence by the triangle inequality again we also have the matching lower bound, thus

for all . The claim is also true for (apply the preceding bound with and ). By replacing with if necessary we may now also assume without loss of generality that , thus

 

for all integers .

Next, for any , and any natural number , we have

so on taking limits as we have . Replacing by gives the matching lower bound, thus we have the conjugation invariance

 

Next, we observe that if are such that is conjugate to both and , then one has the inequality

 

Indeed, if we write for some , then for any natural number one has

where the and terms each appear times. From (2) we see that conjugation by does not affect the norm. Using this and the triangle inequality several times, we conclude that

and the claim (3) follows by sending .

The following special case of (3) will be of particular interest. Let , and for any integers , define the quantity

Observe that is conjugate to both and to , hence by (3) one has

which by (2) leads to the recursive inequality

We can write this in probabilistic notation as

where is a random vector that takes the values and with probability each. Iterating this, we conclude in particular that for any large natural number , one has

where and are iid copies of . We can write where are iid signs.  By the triangle inequality, we thus have

noting that is an even integer.  On the other hand, has mean zero and variance , hence by Cauchy-Schwarz

But by (1), the left-hand side is equal to . Dividing by and then sending , we obtain the claim.

The above theorem reduces such seminorms to abelian groups. It is easy to see from (1) that any torsion element of such groups has zero seminorm, so we can in fact restrict to torsion-free groups, which we now write using additive notation , thus for instance for . We think of as a -module. One can then extend the seminorm to the associated -vector space by the formula , and then to the associated -vector space by continuity, at which point it becomes a genuine seminorm (provided we have ensured the symmetry condition ). Conversely, any seminorm on induces a seminorm on . (These arguments also appear in this paper of Khare and Rajaratnam.)

 

Bi-invariant metrics of linear growth on the free group, II

This post is a continuation of the previous post, which has attracted a large number of comments. I’m recording here some calculations that arose from those comments (particularly those of Pace Nielsen, Lior Silberman, Tobias Fritz, and Apoorva Khare). Please feel free to either continue these calculations or to discuss other approaches to the problem, such as those mentioned in the remaining comments to the previous post.

Let be the free group on two generators , and let be a quantity obeying the triangle inequality

and the linear growth property

for all and integers ; this implies the conjugation invariance

or equivalently

We consider inequalities of the form

or

for various real numbers . For instance, since

we have (1) for . We also have the following further relations:

Proposition 1

• (i) If (1) holds for , then it holds for .
• (ii) If (1) holds for , then (2) holds for .
• (iii) If (2) holds for , then (1) holds for .
• (iv) If (1) holds for and (2) holds for , then (1) holds for .

Proof: For (i) we simply observe that

For (ii), we calculate

giving the claim.

For (iii), we calculate

giving the claim.

For (iv), we calculate

giving the claim.

Here is a typical application of the above estimates. If (1) holds for , then by part (i) it holds for , then by (ii) (2) holds for , then by (iv) (1) holds for . The map has fixed point , thus

For instance, if , then .

Bi-invariant metrics of linear growth on the free group

Here is a curious question posed to me by Apoorva Khare that I do not know the answer to. Let be the free group on two generators . Does there exist a metric on this group which is

• bi-invariant, thus for all ; and
• linear growth in the sense that for all and all natural numbers ?

By defining the “norm” of an element to be , an equivalent formulation of the problem asks if there exists a non-negative norm function that obeys the conjugation invariance

for all , the triangle inequality

for all , and the linear growth

for all and , and such that for all non-identity . Indeed, if such a norm exists then one can just take to give the desired metric.

One can normalise the norm of the generators to be at most , thus

This can then be used to upper bound the norm of other words in . For instance, from (1), (3) one has

A bit less trivially, from (3), (2), (1) one can bound commutators as

In a similar spirit one has

What is not clear to me is if one can keep arguing like this to continually improve the upper bounds on the norm of a given non-trivial group element to the point where this norm must in fact vanish, which would demonstrate that no metric with the above properties on would exist (and in fact would impose strong constraints on similar metrics existing on other groups as well). It is also tempting to use some ideas from geometric group theory (e.g. asymptotic cones) to try to understand these metrics further, though I wasn’t able to get very far with this approach. Anyway, this feels like a problem that might be somewhat receptive to a more crowdsourced attack, so I am posing it here in case any readers wish to try to make progress on it.

Counting objects up to isomorphism: groupoid cardinality

How many groups of order four are there? Technically, there are an enormous number, so much so, in fact, that the class of groups of order four is not even a set, but merely a proper class. This is because any four objects can be turned into a group by designating one of the four objects, say , to be the group identity, and imposing a suitable multiplication table (and inversion law) on the four elements in a manner that obeys the usual group axioms. Since all sets are themselves objects, the class of four-element groups is thus at least as large as the class of all sets, which by Russell’s paradox is known not to itself be a set (assuming the usual ZFC axioms of set theory).

A much better question is to ask how many groups of order four there are up to isomorphism, counting each isomorphism class of groups exactly once. Now, as one learns in undergraduate group theory classes, the answer is just “two”: the cyclic group and the Klein four-group .

More generally, given a class of objects and some equivalence relation on (which one should interpret as describing the property of two objects in being “isomorphic”), one can consider the number of objects in “up to isomorphism”, which is simply the cardinality of the collection of equivalence classes of . In the case where is finite, one can express this cardinality by the formula

thus one counts elements in , weighted by the reciprocal of the number of objects they are isomorphic to.

Example 1 Let be the five-element set of integers between and . Let us say that two elements of are isomorphic if they have the same magnitude: . Then the quotient space consists of just three equivalence classes: , , and . Thus there are three objects in up to isomorphism, and the identity (1) is then just

Thus, to count elements in up to equivalence, the elements are given a weight of because they are each isomorphic to two elements in , while the element is given a weight of because it is isomorphic to just one element in (namely, itself).

Given a finite probability set , there is also a natural probability distribution on , namely the uniform distribution, according to which a random variable is set equal to any given element of with probability :

Given a notion of isomorphism on , one can then define the random equivalence class that the random element belongs to. But if the isomorphism classes are unequal in size, we now encounter a biasing effect: even if was drawn uniformly from , the equivalence class need not be uniformly distributed in . For instance, in the above example, if was drawn uniformly from , then the equivalence class will not be uniformly distributed in the three-element space , because it has a probability of being equal to the class or to the class , and only a probability of being equal to the class .

However, it is possible to remove this bias by changing the weighting in (1), and thus changing the notion of what cardinality means. To do this, we generalise the previous situation. Instead of considering sets with an equivalence relation to capture the notion of isomorphism, we instead consider groupoids, which are sets in which there are allowed to be multiple isomorphisms between elements in (and in particular, there are allowed to be multiple automorphisms from an element to itself). More precisely:

Definition 2 A groupoid is a set (or proper class) , together with a (possibly empty) collection of “isomorphisms” between any pair of elements of , and a composition map from isomorphisms , to isomorphisms in for every , obeying the following group-like axioms:

• (Identity) For every , there is an identity isomorphism , such that for all and .
• (Associativity) If , , and for some , then .
• (Inverse) If for some , then there exists an inverse isomorphism such that and .

We say that two elements of a groupoid are isomorphic, and write , if there is at least one isomorphism from to .

Example 3 Any category gives a groupoid by taking to be the set (or class) of objects, and to be the collection of invertible morphisms from to . For instance, in the category of sets, would be the collection of bijections from to ; in the category of linear vector spaces over some given base field , would be the collection of invertible linear transformations from to ; and so forth.

Every set equipped with an equivalence relation can be turned into a groupoid by assigning precisely one isomorphism from to for any pair with , and no isomorphisms from to when , with the groupoid operations of identity, composition, and inverse defined in the only way possible consistent with the axioms. We will call this the simply connected groupoid associated with this equivalence relation. For instance, with as above, if we turn into a simply connected groupoid, there will be precisely one isomorphism from to , and also precisely one isomorphism from to , but no isomorphisms from to , , or .

However, one can also form multiply-connected groupoids in which there can be multiple isomorphisms from one element of to another. For instance, one can view as a space that is acted on by multiplication by the two-element group . This gives rise to two types of isomorphisms, an identity isomorphism from to for each , and a negation isomorphism from to for each ; in particular, there are two automorphisms of (i.e., isomorphisms from to itself), namely and , whereas the other four elements of only have a single automorphism (the identity isomorphism). One defines composition, identity, and inverse in this groupoid in the obvious fashion (using the group law of the two-element group ); for instance, we have .

For a finite multiply-connected groupoid, it turns out that the natural notion of “cardinality” (or as I prefer to call it, “cardinality up to isomorphism”) is given by the variant

of (1). That is to say, in the multiply connected case, the denominator is no longer the number of objects isomorphic to , but rather the number of isomorphisms from to other objects . Grouping together all summands coming from a single equivalence class in , we can also write this expression as

where is the automorphism group of , that is to say the group of isomorphisms from to itself. (Note that if belong to the same equivalence class , then the two groups and will be isomorphic and thus have the same cardinality, and so the above expression is well-defined.

For instance, if we take to be the simply connected groupoid on , then the number of elements of up to isomorphism is

exactly as before. If however we take the multiply connected groupoid on , in which has two automorphisms, the number of elements of up to isomorphism is now the smaller quantity

the equivalence class is now counted with weight rather than due to the two automorphisms on . Geometrically, one can think of this groupoid as being formed by taking the five-element set , and “folding it in half” around the fixed point , giving rise to two “full” quotient points and one “half” point . More generally, given a finite group acting on a finite set , and forming the associated multiply connected groupoid, the cardinality up to isomorphism of this groupoid will be , since each element of will have isomorphisms on it (whether they be to the same element , or to other elements of ).

The definition (2) can also make sense for some infinite groupoids; to my knowledge this was first explicitly done in this paper of Baez and Dolan. Consider for instance the category of finite sets, with isomorphisms given by bijections as in Example 3. Every finite set is isomorphic to for some natural number , so the equivalence classes of may be indexed by the natural numbers. The automorphism group of has order , so the cardinality of up to isomorphism is

(This fact is sometimes loosely stated as “the number of finite sets is “, but I view this statement as somewhat misleading if the qualifier “up to isomorphism” is not added.) Similarly, when one allows for multiple isomorphisms from a group to itself, the number of groups of order four up to isomorphism is now

because the cyclic group has two automorphisms, whereas the Klein four-group has six.

In the case that the cardinality of a groupoid up to isomorphism is finite and non-empty, one can now define the notion of a random isomorphism class in drawn “uniformly up to isomorphism”, by requiring the probability of attaining any given isomorphism class to be

thus the probability of being isomorphic to a given element will be inversely proportional to the number of automorphisms that has. For instance, if we take to be the set with the simply connected groupoid, will be drawn uniformly from the three available equivalence classes , with a probability of attaining each; but if instead one uses the multiply connected groupoid coming from the action of , and draws uniformly up to isomorphism, then and will now be selected with probability each, and will be selected with probability . Thus this distribution has accounted for the bias mentioned previously: if a finite group acts on a finite space , and is drawn uniformly from , then now still be drawn uniformly up to isomorphism from , if we use the multiply connected groupoid coming from the action, rather than the simply connected groupoid coming from just the -orbit structure on .

Using the groupoid of finite sets, we see that a finite set chosen uniformly up to isomorphism will have a cardinality that is distributed according to the Poisson distribution of parameter , that is to say it will be of cardinality with probability .

One important source of groupoids are the fundamental groupoids of a manifold (one can also consider more general topological spaces than manifolds, but for simplicity we will restrict this discussion to the manifold case), in which the underlying space is simply , and the isomorphisms from to are the equivalence classes of paths from to up to homotopy; in particular, the automorphism group of any given point is just the fundamental group of at that base point. The equivalence class of a point in is then the connected component of in . The cardinality up to isomorphism of the fundamental groupoid is then

where is the collection of connected components of , and is the order of the fundamental group of . Thus, simply connected components of count for a full unit of cardinality, whereas multiply connected components (which can be viewed as quotients of their simply connected cover by their fundamental group) will count for a fractional unit of cardinality, inversely to the order of their fundamental group.

This notion of cardinality up to isomorphism of a groupoid behaves well with respect to various basic notions. For instance, suppose one has an -fold covering map of one finite groupoid by another . This means that is a functor that is surjective, with all preimages of cardinality , with the property that given any pair in the base space and any in the preimage of , every isomorphism has a unique lift from the given initial point (and some in the preimage of ). Then one can check that the cardinality up to isomorphism of is times the cardinality up to isomorphism of , which fits well with the geometric picture of as the -fold cover of . (For instance, if one covers a manifold with finite fundamental group by its universal cover, this is a -fold cover, the base has cardinality up to isomorphism, and the universal cover has cardinality one up to isomorphism.) Related to this, if one draws an equivalence class of uniformly up to isomorphism, then will be an equivalence class of drawn uniformly up to isomorphism also.

Indeed, one can show that this notion of cardinality up to isomorphism for groupoids is uniquely determined by a small number of axioms such as these (similar to the axioms that determine Euler characteristic); see this blog post of Qiaochu Yuan for details.

The probability distributions on isomorphism classes described by the above recipe seem to arise naturally in many applications. For instance, if one draws a profinite abelian group up to isomorphism at random in this fashion (so that each isomorphism class of a profinite abelian group occurs with probability inversely proportional to the number of automorphisms of this group), then the resulting distribution is known as the Cohen-Lenstra distribution, and seems to emerge as the natural asymptotic distribution of many randomly generated profinite abelian groups in number theory and combinatorics, such as the class groups of random quadratic fields; see this previous blog post for more discussion. For a simple combinatorial example, the set of fixed points of a random permutation on elements will have a cardinality that converges in distribution to the Poisson distribution of rate (as discussed in this previous post), thus we see that the fixed points of a large random permutation asymptotically are distributed uniformly up to isomorphism. I’ve been told that this notion of cardinality up to isomorphism is also particularly compatible with stacks (which are a good framework to describe such objects as moduli spaces of algebraic varieties up to isomorphism), though I am not sufficiently acquainted with this theory to say much more than this.