In the field of analysis, it is common to make a distinction between “hard”, “quantitative”, or “finitary” analysis on one hand, and “soft”, “qualitative”, or “infinitary” analysis on the other. “Hard analysis” is mostly concerned with finite quantities (e.g. the cardinality of finite sets, the measure of bounded sets, the value of convergent integrals, the norm of finite-dimensional vectors, etc.) and their quantitative properties (in particular, upper and lower bounds). “Soft analysis”, on the other hand, tends to deal with more infinitary objects (e.g. sequences, measurable sets and functions, -algebras, Banach spaces, etc.) and their qualitative properties (convergence, boundedness, integrability, completeness, compactness, etc.). To put it more symbolically, hard analysis is the mathematics of
,
,
, and
[1]; soft analysis is the mathematics of 0,
,
, and
.
At first glance, the two types of analysis look very different; they deal with different types of objects, ask different types of questions, and seem to use different techniques in their proofs. They even use[2] different axioms of mathematics; the axiom of infinity, the axiom of choice, and the Dedekind completeness axiom for the real numbers are often invoked in soft analysis, but rarely in hard analysis. (As a consequence, there are occasionally some finitary results that can be proven easily by soft analysis but are in fact impossible to prove via hard analysis methods; the Paris-Harrington theorem gives a famous example.) Because of all these differences, it is common for analysts to specialise in only one of the two types of analysis. For instance, as a general rule (and with notable exceptions), discrete mathematicians, computer scientists, real-variable harmonic analysts, and analytic number theorists tend to rely on “hard analysis” tools, whereas functional analysts, operator algebraists, abstract harmonic analysts, and ergodic theorists tend to rely on “soft analysis” tools. (PDE is an interesting intermediate case in which both types of analysis are popular and useful, though many practitioners of PDE still prefer to primarily use just one of the two types. Another interesting transition occurs on the interface between point-set topology, which largely uses soft analysis, and metric geometry, which largely uses hard analysis. Also, the ineffective bounds which crop up from time to time in analytic number theory are a sort of hybrid of hard and soft analysis. Finally, there are examples of evolution of a field from soft analysis to hard (e.g. Banach space geometry) or vice versa (e.g. recent developments in extremal combinatorics, particularly in relation to the regularity lemma).)
It is fairly well known that the results obtained by hard and soft analysis respectively can be connected to each other by various “correspondence principles” or “compactness principles”. It is however my belief that the relationship between the two types of analysis is in fact much closer[3] than just this; in many cases, qualitative analysis can be viewed as a convenient abstraction of quantitative analysis, in which the precise dependencies between various finite quantities has been efficiently concealed from view by use of infinitary notation. Conversely, quantitative analysis can often be viewed as a more precise and detailed refinement of qualitative analysis. Furthermore, a method from hard analysis often has some analogue in soft analysis and vice versa, though the language and notation of the analogue may look completely different from that of the original. I therefore feel that it is often profitable for a practitioner of one type of analysis to learn about the other, as they both offer their own strengths, weaknesses, and intuition, and knowledge of one gives more insight[4] into the workings of the other. I wish to illustrate this point here using a simple but not terribly well known result, which I shall call the “finite convergence principle” (thanks to Ben Green for suggesting this name; Jennifer Chayes has also suggested the “metastability principle”). It is the finitary analogue of an utterly trivial infinitary result – namely, that every bounded monotone sequence converges – but sometimes, a careful analysis of a trivial result can be surprisingly revealing, as I hope to demonstrate here.
Before I discuss this principle, let me first present an informal, incomplete, and inaccurate “dictionary” between soft and hard analysis, to try to give a rough idea of the (partial) correspondences between the two:
| Soft analysis | Hard analysis |
| x finite | x bounded (e.g. x = O(1)) |
| x vanishes | x small (e.g. |
| x infinite | x large (e.g. |
| Quantitative decay bound (e.g. |
|
| f uniformly continuous | Lipschitz or Hölder bound on f (e.g. |
| E compact | Metric entropy bound on E |
| E is Lebesgue measurable | E is (quantitatively) approximated by bounded complexity sets |
| V is generated by S | V is an algorithm initialised by S |
| u locally extremises F(u) | u has no nearby competitor with significantly better value of F |
One can draw two conclusions from this table:
- Soft analysis statements can often be stated both succinctly and rigorously, by using precisely defined and useful concepts (e.g. compactness, measurability, etc.). In hard analysis, one usually has to sacrifice one or the other: either one is rigorous but verbose (using lots of parameters such as
, N, etc.), or succinct but “fuzzy” (using intuitive but vaguely defined concepts such as “size”, “complexity”, “nearby”, etc.).
- A single concept in soft analysis can have multiple hard analysis counterparts; a “naive” translation of a statement in soft analysis into hard analysis may be incorrect. (In particular, one should not use the above table blindly to convert from one to the other.)
Anyway, back to the finite convergence principle. The infinite convergence principle is well known, though perhaps not by this name, to anyone who has taken undergraduate analysis:
Infinite convergence principle. Every bounded monotone sequence
of real numbers is convergent.
This basic principle – essentially equivalent to the Dedekind completeness axiom for the real numbers – is of course fundamental to many parts of infinitary analysis, most obviously in the theory of infinite sequences and series, but it also is implicit in just about any context in which one studies an “infinite” object (e.g. an infinite-dimensional vector space) by expressing it as a monotone limit of “finite” objects. It is undoubtedly an important tool in soft analysis. What, then, is its counterpart in hard analysis?
We will answer this question presently, but let us first make the infinite convergence principle a bit more quantitative. We may as well normalise the bounded sequence to lie between 0 and 1. Expanding out the “epsilon-delta” definition of convergence, we obtain
Infinite convergence principle (again). If
, then there exists a real number x such that for every
, there exists an N such that
for all
.
There are quite a lot of quantifiers here. One can cut down the complexity a little bit by replacing the notion of a convergent sequence with that of a Cauchy sequence. This lets us eliminate the need for a limit x, which does not have an obvious finitary counterpart. So we get
Infinite convergence principle (yet again). If
and
, there exists an N such that
for all
.
Note now that one does not need the real number system to make this principle both meaningful and non-trivial; the principle already works quite well when restricted to the rationals. (Exercise: prove this principle for the rationals without constructing the real number system.) Informally speaking, this principle asserts that every bounded monotone sequence is eventually stable up to error .
Now let’s try to find the finitary (quantitative) equivalent of this principle. The most naive thing to do is simply to replace the infinite sequence by a finite sequence, thus
Finite convergence principle (first attempt). If
and
, there exists an N such that
for all
.
But this is trivially true; one can simply set N equal to M (or any number larger than M). So one needs to strengthen the claim. What about making N be independent of M, and only dependent on ?
Finite convergence principle (second attempt). If
and
, there exists an
depending only on
such that
for all
.
But this is trivially false; consider for instance a sequence which equals zero except at i=M, at which point we jump up to
. We are not going to get the Cauchy property unless we set N to be as large as M… but we can’t do that if we only want N to depend on
.
So, is there anything non-trivial that one can say at all about finite bounded monotone sequences? Well, we have the pigeonhole principle:
Pigeonhole principle. If
and
is such that
, there exists an
such that
.
Indeed, if the gaps between each element of the sequence and the next
were always larger than
, then
would exceed
, a contradiction. This principle is true, but it is too weak to be considered a true finitary version of the infinite convergence principle; indeed, we see that the pigeonhole principle easily implies
Weak infinite convergence principle. If
, then
.
but does not obviously imply the full infinite convergence principle.
The problem is that the pigeonhole principle only establishes instantaneous stability of the sequence at some point n, whereas the infinite convergence principle concludes the permanent stability of the sequence after some point N. To get a better finitary match to the infinite convergence principle, we need to extend the region of stability that the pigeonhole principle offers. Now, one can do some trivial extensions such as
Pigeonhole principle (second version). If
and
and
is such that
, there exists
such that
for all
,
which one can quickly deduce from the first pigeonhole principle by considering the sparsified sequence . But this is only a little bit better, as it now gives the infinitary statement
Slightly less weak infinite convergence principle. If
, then
for all k,
but is still not strong enough to imply the infinite convergence principle in its full strength. Nevertheless, it shows that we can extend the realm of stability offered by the pigeonhole principle. One can for instance sparsify further, replacing n+k with 2n:
Pigeonhole principle (third version). If
and
and
is such that
, there exists
such that
for all
.
This can be proven by applying the first version of the pigeonhole principle to the sparsified sequence . This corresponds to an infinite convergence principle in which the conclusion is that
.
One can of course keep doing this, achieving various sparsified versions of the pigeonhole principle which each capture part of the infinite convergence principle. To get the full infinite convergence principle, one cannot use any single such sparsified version of the pigeonhole principle, but instead must take all of them at once. This is the full strength of the finite convergence principle:
Finite convergence principle. If
and
is a function and
is such that
is sufficiently large depending on F and
, then there exists
such that
for all
.
This principle is easily proven by appealing to the first pigeonhole principle with the sparsified sequence where the indices are defined recursively by
and
. This gives an explicit bound on M as
. Note that the first pigeonhole principle corresponds to the case
, the second pigeonhole principle to the case
, and the third to the case
. A particularly useful case for applications is when F grows exponentially in N, in which case M grows tower-exponentially in
.
Informally, the above principle asserts that any sufficiently long (but finite) bounded monotone sequence will experience arbitrarily high-quality amounts of metastability with a specified error tolerance , in which the duration F(N) of the metastability exceeds the time N of onset of the metastability by an arbitrary function F which is specified in advance.
Let us now convince ourselves that this is the true finitary version of the infinite convergence principle, by deducing them from each other:
The finite convergence principle implies the infinite convergence principle. Suppose for contradiction that the infinite convergence principle failed. Untangling the quantifiers, this asserts that there is an infinite sequence and an
with the property that, given any positive integer N, there exists a larger integer
such that
. But this contradicts the finite convergence principle.
The infinite convergence principle implies the finite convergence principle. Suppose for contradiction that the finite convergence principle failed. Untangling the quantifiers, this asserts that there exists and a function F, together with a collection
of bounded monotone sequences whose length
goes to infinity, such that for each one of these sequences, there does not exist
such that
for all
. Let us extend each of the finite bounded sequences to infinite bounded sequences in some arbitrary manner, e.g. defining
whenever
. The space of all bounded sequences is well-known[5] to be sequentially compact in the product topology, thus after refining the i labels to a subsequence if necessary, we can assume that the sequences
converge in the product topology (i.e. pointwise) to a new limit sequence
. Since each of the original sequences were bounded in the interval [0,1] and monotone, we see that the limit sequence is also. Furthermore, we claim that there does not exist any
for which
for all
. Indeed, if this were the case, then by pointwise convergence we would also have
for all
and all sufficiently large i, but this contradicts the construction of the
. But now we see that this infinite bounded monotone sequence
contradicts the infinite convergence principle.
One can draw some morals from the above discussion:
- The finitary version of an infinitary statement can be significantly more verbose and ugly-looking than the infinitary original, and the arrangement of quantifiers becomes crucial.
- The “naive” finitisation of an infinitary statement is often not the correct one.
- While the finitary version of an infinitary statement is indeed quantitative, the bounds obtained can be quite poor (e.g. tower-exponential or worse).
- The deduction of the infinitary statement from the finitary one is quite short, as long as one is willing to work indirectly (arguing by contradiction).
- The deduction of the finitary statement from the infinitary one is a bit more complicated, but still straightforward, and relies primarily on compactness.
- In particular, the equivalence of the finitary and infinitary formulations requires a non-trivial amount of infinitary mathematics (though in this particular case, we can at least leave the ultrafilters out of it).
These morals apply not only to the finite and infinite convergence principle, but to many other pairs of finitary and infinitary statements, for instance Szemerédi’s theorem on one hand and the Furstenberg recurrence theorem on the other, as briefly discussed in my Simons lecture on these topics. (In these contexts, the correspondence between the finitary and infinitary statements is known as the Furstenberg correspondence principle.)
— Applications —
So, we’ve now extracted a quantitative finitary equivalent of the infinitary principle that every bounded monotone sequence converges. But can we actually use this finite convergence principle for some non-trivial finitary application? The answer is a definite yes: the finite convergence principle (implicitly) underlies the famous Szemerédi regularity lemma, which is a major tool in graph theory, and also underlies some rather less well known regularity lemmas, such as the arithmetic regularity lemma of Green. More generally, this principle seems to often arise in any finitary application in which tower-exponential bounds are inevitably involved.
Before plunging into these applications, let us first establish a Hilbert space version[6] of the convergence principle. Given a (closed) subspace X of a Hilbert space H, and a vector , let
be the orthogonal projection from v onto X. If X is finite dimensional, then this projection can be defined in a finitary way, for instance by using the Gram-Schmidt orthogonalisation procedure to X. If X is infinite dimensional, then even the existence of the orthogonal projection is not completely trivial, and in fact relies ultimately on the infinite convergence principle. Closely related to the existence of this projection is the following monotone continuity property:
Hilbert space infinite convergence principle. Let
be a nested sequence of subspaces of a Hilbert space H, and let
be the monotone closed limit of the
. Then for any vector v,
converges strongly in H to
.
As with the infinite convergence principle in [0,1], there is a Cauchy sequence version which already captures the bulk of the content:
Hilbert space infinite convergence principle (again). Let
be a nested sequence of subspaces of a Hilbert space H, and let
. Then for any vector v there exists N such that
for all
.
One can deduce this principle from the analogous principle in [0,1] by first normalising , and then observing from Pythagoras’ theorem that
(which one should view as the energy of
as measured relative to v) is a bounded monotone sequence from 0 to 1. Applying the infinite convergence principle, followed by Pythagoras’ theorem yet again, we obtain the claim. Once one sees this, one immediately concludes that there is also a finitary equivalent:
Hilbert space finite convergence principle. If
and
, and
is such that M is sufficiently large depending on F and
, then for any vector v with
there exists
such that
for all
.
Informally, given a long enough sequence of nested subspaces, and a given bounded vector v, one can find an arbitrarily good region of metastability in the orthogonal projections of v into these subspaces.
From this principle one can then quickly deduce the Szemerédi regularity lemma as follows. Let G = (V,E) be a graph. One can think of the adjacency matrix of this graph as an element of the (finite-dimensional) Hilbert space
, where the product space
is given normalised counting measure (and the discrete sigma-algebra
). We can construct a nested sequence
of
-algebras in
(which one can think of as a sequence of increasingly fine partitions of V), together with the attendant sequence
of subspaces (this corresponds to functions on
which are constant on any product of pair of cells in the partition), by the following greedy algorithm[7]:
- Initialise
to be the trivial
-algebra (i.e. the trivial partition).
- Given
, let
be the orthogonal projection of
to the space
(thus the value on any product of cells is just the edge density between that pair of cells), and let
be the deviation of the graph from its density.
- Let
be sets in V which maximise the discrepancy
.
- Let
be the
-algebra generated by
and
. Now increment n by n+1 and return to Step 2.
Let and
be a function. Applying the Hilbert space finite convergence principle to the above sequence of vector spaces, we obtain some N with some bounded size (depending on
and F) such that
(*)
for all . By a further application of the pigeonhole principle (for Hilbert spaces), one can find
such that
.
What this basically means is that the partition is very regular, in that even the greediest way to refine this partition does not significantly capture any more of the fluctuations of the graph G. By choosing F to be a suitable exponentially growing function, one can make the regularity of this partition exceed the number of cells (which is basically
) in the partition
, which is “within epsilon” of the partition
in the sense of (*). Putting all this together, one can get a strong version of the Szemerédi regularity lemma, which implies the usual formulation by a simple argument; see my paper on this topic for further discussion. The choice of F being exponential is what results in the notorious tower-exponential bounds in this regularity lemma (which are necessary, thanks to a result of Gowers). But one can reduce F to, say, a polynomial, resulting in more civilised bounds but with a weaker regularity conclusion. Such a “weak regularity lemma” was for instance established by Frieze and Kannan, and also underlies the “generalised Koopman von Neumann theorem” which is a key component of my result with Ben Green establishing long arithmetic progressions in the primes. In the opposite direction, various flavours of “strong regularity lemma” have appeared in the literature, for instance in this paper of Alon and Shapira, and also turn out to be convenient ways to formulate hypergraph versions of the regularity lemma of adequate strength to imply non-trivial theorems (such as Szemerédi’s theorem).
Rather than using sets which maximise discrepancy, one can also use sublevel sets of the eigenvectors of the adjacency matrix corresponding to the largest eigenvalues of the matrix to generate the partition; see this paper of Frieze and Kannan for details of a closely related construction.
The appearance of spectral theory (eigenvalues and eigenvectors) into this topic brings one in contact with Fourier analysis, especially if one considers circulant matrices (which correspond in graph-theoretic terms to Cayley graphs on a cyclic group). This leads us towards the arithmetic regularity lemma of Green, which regularises a bounded function f on a finite abelian group G in terms of a partition generated by the sublevel sets (Bohr sets) of a bounded number of characters; the precise formulation is a bit lengthy to state properly, although it simplifies substantially in the “finite field model” case when G is a vector space over a small finite field (e.g. ). This arithmetic regularity lemma can also be established using the finite convergence principle (in either the numerical form or the Hilbert space form). Indeed, if we let
and let
be the vector space generated by the characters associated to the n largest Fourier coefficients of f, then by applying the finite convergence principle (with v = f) we can locate a metastable region, where there is not much going on (in an
sense) between
and
for some (exponentially growing) function F, thus there is a “spectral gap” of sorts between the N largest Fourier coefficients and the coefficients ranked N+F(N) and beyond. The sublevel sets of characters associated to the N largest coefficients can then be used to regularise the original function f. Similar ideas also appear in an old paper of Bourgain, and in a paper of Green and Konyagin.
— A non-finitisable statement —
One may think from the above discussion that every infinitary statement concerning, say, the natural numbers, has a finitary analogue which is equivalent to it. It turns out that this is not quite the case (and in fact some subtle issues in logic come in), even for very “natural” and “non-pathological” infinitary statements. In particular, the following innocuous-looking infinitary statement is basically non-finitisable:
Infinite pigeonhole principle. If the natural numbers are divided into finitely many colour classes, then one of the colour classes is infinite.
This principle is of course a triviality in the infinitary world, and there are some obvious candidates for finitary versions (e.g. the finite pigeonhole principle), but they are not equivalent to the infinitary principle the same way that the finite convergence principle is equivalent to the infinite convergence principle; there is a failure of compactness here. There is a finitary version (of sorts), but it is somewhat difficult to state. Define a set function to be any function f which takes a finite set A of natural numbers as input, and returns a natural number F(A) as output. Let us say that a set function F is asymptotically stable near infinite sets[8] if, given any sequence of finite sets of natural numbers which converges to an infinite set
in the sense that for any finite set I,
for all sufficiently large n, the numbers
are constant for sufficiently large n. For instance, the “least element” set function
(adopting the non-standard convention that the infimum of the empty set is 0) is asymptotically stable, but the “cardinality” set function
is not. Anyway, the correct “finitary” version of the infinite pigeonhole principle is
“Finitary” infinite pigeonhole principle. Let F be an set function that is asymptotically stable near infinite sets, and let k be a positive integer. Then there exists a positive integer N with the property that whenever the set {1,…,N} is divided into k colour classes, at least one of the colour classes A has the property that |A| > F(A).
It is a good exercise to see that this principle is equivalent to the infinite pigeonhole principle. Note that the plain old pigeonhole principle essentially corresponds to the case when F is a constant function – and is thus definitely a very special case. The case when for some fixed function f is already very interesting – it is the 1-uniform case of a “strong Ramsey theorem”and is barely provable by finitary means (try it, say for k=10 and
. What quantitative bound for N do you get?), although the general case of that theorem is not (but does follow easily from the above principle), thanks to the Paris-Harrington theorem. The assumption of asymptotic stability of F near infinite sets is necessary, as one can see by considering the counterexample F(A) := |A|.
I am enclosing “finitary” in quotes because while most of the assertion of this principle is finitary, one part still is not, which is the notion of “asymptotically stable near infinite sets”. This is a notion which cannot be precisely formulated in a purely finitary manner, even though the notion of a set function is basically a finitary concept (ignoring for now a subtle issue about what “function” means). If one insists on working in a finitary setting, then one can recast the infinite pigeonhole principle as a schema of finitary principles, one for each set function F that is asymptotically stable near infinite sets, but in order to work out exactly which set functions are asymptotically stable near infinite sets or not requires infinitary mathematics. (And for some (constructible, well-defined) set functions, the asymptotic stability near infinite sets is undecidable; this fact is closely related to the undecidability of the halting problem and is left as an exercise to the reader.)
The topic of exactly which statements in infinitary mathematics are “truly infinitary” is a fascinating one, and is basically a question in reverse mathematics, but we will not be able to discuss it here.
(I am indebted to Harvey Friedman for discussions on the Paris-Harrington theorem and the infinite pigeonhole principle.)
— Footnotes —
(N.B. Footnotes were created following the suggestions from this post by santoki.)
[1] One can subdivide hard analysis into further subcategories by inspecting what kind of inequalities are used. There is “exact hard analysis” where one really uses ; “quasi-exact hard analysis” in which one is willing to lose absolute constants (and so one sees notation such as O(),
, or
); “logarithmically coarse hard analysis” in which one is willing to lose quantities such as
which are “logarithmic” in some key parameter N; and “polynomially coarse hard analysis” in which one is willing to lose quantities such as
which are polynomial in key parameters. Finally, there is “coarse analysis” in which one is willing to lose arbitrary functions of key parameters. The relationships between these flavours of hard analysis are interesting, but will have to wait to be discussed elsewhere.
[2] One can use these axioms to make finer distinctions, for instance “strongly finitary” analysis, in which one is not even willing to use real numbers, but instead only works with finite complexity numbers (e.g. rationals), and “strongly infinitary” analysis, in which one freely uses the axiom of choice (or related concepts such as ultrafilters). There are also hybrids between finitary and infinitary analysis, such as “pre-infinitary” analysis, in which one takes sequences of increasingly large or complex objects, and uses phrases such as “passing to a subsequence if necessary” a lot, but does not actually “jump to the limit”; we also have “pseudo-finitary” analysis, of which non-standard analysis is the most prominent example, in which infinitary methods are re-expressed using infinitesimals or other pseudo-finitary objects. Again, these distinctions will have to wait to be discussed elsewhere.
[3] There are rigorous results from proof theory, such as Herbrand’s theorem, which can allow one to automatically convert certain types of qualitative arguments into quantitative ones, but there appears to be only a small amount of literature applying these general results in logic to actual soft analysis arguments. (See the comments to this post for some recent developments in this area.)
[4] For instance, in my result with Ben Green establishing arbitrarily long arithmetic progressions of primes, the argument was (necessarily) finitary in nature, but it was absolutely essential for us to be aware of the infinitary arguments and intuition that had been developed in ergodic theory, as we had to adapt such arguments to the finitary setting in order to conclude our proof, and it would have far less evident how to discover such arguments if we were always restricted to looking at finitary settings. In general, it seems that infinitary methods are good for “long-range” mathematics, as by ignoring all quantitative issues one can move more rapidly to uncover qualitatively new kinds of results, whereas finitary methods are good for “short-range” mathematics, in which existing “soft” results are refined and understood much better via the process of making them increasingly sharp, precise, and quantitative. I feel therefore that these two methods are complementary, and are both important to deepening our understanding of mathematics as a whole.
[5] This looks like Tychonoff’s theorem, but because we require sequential compactness here rather than topological compactness, the result here is in fact much closer in spirit to the Arzelà-Ascoli theorem. In particular, the axiom of choice is not actually used here, instead one repeatedly uses the Bolzano-Weierstrass theorem for the interval [0,1] followed by a diagonalisation argument. The astute reader here will observe that the Bolzano-Weierstrass theorem is essentially equivalent to the infinite convergence principle! Fortunately, there is no circularity here, because we are only using this theorem in order to deduce the finite convergence principle from the infinite, and not the other way around.
[6] One could also view this as a “noncommutative” or “quantum” version of the convergence principle, but this is somewhat of an abuse of terminology, despite the presence of the Hilbert space, since we don’t actually have any noncommutativity or any other quantum weirdness going on.
[7] One can also replace this greedy algorithm by a random algorithm, in which each is obtained from
by adding a neighbourhood
of a randomly chosen vertex
in V. This use of randomisation appears in the infinitary setting in this paper of myself, and in the finitary setting in this paper of Ishigami.
[8] This notation is very roughly equivalent to the notion of a function F(A) defined for all sets of integers (both finite and infinite) which can always be “computed” in “finite time” if the set is infinite. But one should take this informal definition with a large grain of salt: while there is indeed an algorithm for computing F(A) for any given set A which will eventually give the right answer, you might not be able to tell when the algorithm has finished! A good example is the function which is asymptotically stable near infinite sets: you can “compute” this function for any set A by initialising the answer to 0, running a counter n from 0 to infinity, and resetting the answer permanently to n the first time n lies in A. As long as A is non-empty, this algorithm terminates in finite time with the correct answer; if A is empty, the algorithm gives the right answer from the beginning, but you can never be sure of this fact! In contrast, the cardinality |A| of a possibly infinite set A cannot be computed even in this rather unsatisfactory sense of having a running “provisional answer” which is guaranteed to eventually be correct.
[Update, May 24: Typos corrected. A distinction drawn between the strong Ramsey theorem (a theorem that can be stated in finitary mathematics), and the Paris-Harrington theorem (which shows that the strong Ramsey theorem is unprovable by finitary means). Acknowledgment to Harvey Friedman added, as well as a link to reverse mathematics.]
[Update, May 25: functional analysis changed to operator algebras. Footnote [3] modified in view of recent comments.]
[Update, May 31: corrected to “
when A is non-empty, and 0 if A is empty”.]
[Update, Aug 19, 2008: Definition of asymptotic stability corrected; thanks to Jaime Gaspar for pointing out the problem.]

80 comments
Comments feed for this article
28 August, 2012 at 7:18 am
Hard analysis, soft analysis — The Endeavour
[…] I was trained as a bird, but I’ve become more of a frog over time. Of course these categories are not exclusive. Frogs sometimes act as birds and vice versa. The categories of hard and soft analysis are not exclusive either. See Terry Tao’s article on relating hard and soft analysis. […]
1 October, 2012 at 1:02 am
Functional Analysis – Introduction. Part II « Noncommutative Analysis
[…] of substance, which applies to concrete cases in analysis, that does not involve some kind of hard analysis, some epsilonaustics, some sweat. In our example, the hard analysis comes in the proof of the […]
25 October, 2012 at 10:10 am
Walsh’s ergodic theorem, metastability, and external Cauchy convergence « What’s new
[…] which is useful in situations in which one does not expect a uniform convergence rate; see this previous blog post for some discussion of metastability. When interpreted in a finitary setting, this concept requires […]
23 November, 2012 at 3:57 am
The three Moirai, continued « chorasimilarity
[…] Now the construction is finished, let us let the Moirai to do their job. Finally, I shall recall my real goal, which I have never forgot. The real goal is to pass from understanding of the power of this lambda calculus sector of graphic lambda calculus to the real deal, called “computing with space”, namely to understand space from a computational perspective, not as a given receptacle, but as a small list of procedures along with some impossible to verify assertions (like that we may rescale indefinitely space), see “emergent algebras”, which can always be eliminated a posteriori, by a kind of finitization procedure. […]
3 December, 2012 at 5:35 pm
The spectral proof of the Szemeredi regularity lemma « What’s new
[…] with for all . Applying (3) and the pigeonhole principle (or the finite convergence principle, see this blog post), we can find such […]
10 May, 2013 at 10:05 pm
Bird’s-eye views of Structure and Randomness (Series) | Abstract Art
[…] Analogies between finitary and infinitary math (adapted from “Soft analysis, hard analysis and the finite convergence principle“) […]
17 May, 2013 at 11:50 am
andrescaicedo
Jennifer Chayes’s link is outdated. The current link should be http://research.microsoft.com/en-us/um/people/jchayes/
[Corrected, thanks – T.]
17 May, 2013 at 9:28 pm
Frank
Dear professor:![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is Cauchy as well. The compactness of
is Cauchy as well. The compactness of ![[0,1]^\omega](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E%5Comega&bg=ffffff&fg=545454&s=0&c=20201002) depends on that, I think.
depends on that, I think.
Sorry for my ignorance. In my opinion, the proof of the part (the infinite convergence principle implying the finite convergence principle) is imperfect. The compactness or completeness of the real line might as well be avoided, since the theorem, i.e, the monotone sequence of rational numbers on
20 May, 2013 at 7:04 am
Analogies between finitary and infinitary math | Abstract Art
[…] [1.3] Soft analysis, hard analysis, and the finite convergence principle […]
26 January, 2023 at 1:35 am
Anonymous
Dear professor Tao, do you have something in mind about something in operator algebra that has some analog in “hard analysis”? Because to my knowledge (which is surely still lacking in many ways), operator algebra in the sense of Connes feels extremely algebraic and doesn’t feel like the usual functional analysis that interacts with PDEs (but sorry if I’m wrong about this)
29 May, 2013 at 12:40 pm
Topological order for mixed states | Tobias J. Osborne's research notes
[…] The definition provided by Hastings is much closer in spirit with this second definition. (It’s worth noting that by working in the infinite lattice size limit we can avoid lots of s and s; we can make our soft analysis definition a hard analysis definition if we like in the standard way.) […]
30 August, 2013 at 12:20 pm
O intâlnire cu informatica teoretică românească: FMI@150 Ziua I | Isarlâk
[…] de faptul că domeniul este unul interesant vă puteți convinge de exemplu citind această discuție pe blogul lui Terry Tao. Ar fi interesant de văzut câte din lucrurile din acest domeniu pot fi automatizate. Impresia pe […]
18 September, 2015 at 4:46 pm
The logarithmically averaged Chowla and Elliott conjectures for two-point correlations; the Erdos discrepancy problem | What's new
[…] at some point one must reach a metastable region (cf. the finite convergence principle discussed in this previous blog post), within which very little mutual information can be shared between the sequence and the graph . […]
12 December, 2016 at 6:40 pm
Hilbert’s Curve, and the usefulness of infinite results in a finite world | Coding Craze
[…] Soft analysis, hard analysis, and the finite convergence principle c++ programs […]
14 December, 2016 at 8:28 am
Hilbert’s Curve, and the usefulness of infinite results in a finite world | Coding Tweaks
[…] Soft analysis, hard analysis, and the finite convergence principle c++ programs […]
27 January, 2017 at 6:18 am
Hard analysis, soft analysis
[…] I was trained as a bird, but I’ve become more of a frog over time. Of course these categories are not exclusive. Frogs sometimes act as birds and vice versa. The categories of hard and soft analysis are not exclusive either. See Terry Tao’s article on relating hard and soft analysis. […]
19 July, 2017 at 2:48 pm
An Epsilon of Mathematics
[…] https://terrytao.wordpress.com/2007/05/23/soft-analysis-hard-analysis-and-the-finite-convergence-pri… […]
23 July, 2017 at 7:53 am
elienasrallah
Reblogged this on Elie Nasrallah.
30 July, 2017 at 12:51 pm
franchb
Reblogged this on irusin.
14 May, 2018 at 12:52 pm
Finitary versions of theorems – Write down what you’ve done
[…] https://terrytao.wordpress.com/2007/05/23/soft-analysis-hard-analysis-and-the-finite-convergence-pri… […]
16 March, 2019 at 12:19 pm
An Epsilon of Mathematics … draft …
[…] https://terrytao.wordpress.com/2007/05/23/soft-analysis-hard-analysis-and-the-finite-convergence-pri… […]
12 May, 2019 at 12:44 pm
Rationality from Irrationality Part 3: From Matching Pennies to Matching Regrets – Technicalities
[…] proof will be a long sequence of hard (as opposed to soft) analysis problems centered around the following main idea: for , we want to […]
15 August, 2019 at 11:31 am
Quantitative bounds for critically bounded solutions to the Navier-Stokes equations | What's new
[…] the use of compactness by more complicated substitutes that give effective bounds; see for instance these previous blog posts for more discussion. I therefore was interested in trying to obtain a […]
17 March, 2020 at 1:33 pm
Vilhelm Agdur
Regarding the very last part, with the “finitary infinitary pigeonhole principle”, does this result crucially depend on the notion of being asymptotically stable near infinite sets quantifying over all sets, or do we still get something interesting if we weaken it to an almost-surely w.r.t. the uniform measure?
In particular, I mean this: suppose we have a function such that for a randomly chosen
such that for a randomly chosen  , for any sequence
, for any sequence 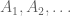 of finite sets convergent to
of finite sets convergent to  , w.p.1 the sequence
, w.p.1 the sequence 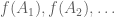 is eventually constant and equal to
is eventually constant and equal to 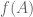 . Do we still get an interesting conclusion?
. Do we still get an interesting conclusion?
3 June, 2020 at 4:07 pm
247B, Notes 4: almost everywhere convergence of Fourier series | What's new
[…] the correspondence Serre discusses is slightly different from the one I discuss for instance in here or here, although there seems to be a common theme of “compactness” (or of model […]
2 August, 2020 at 10:29 am
What proof mining is about, Part IV: Kohlenbach & friends - The Proof Theory Blog
[…] Tao in 2007 during his work on multiple ergodic averages, introduced at the time to the public in this blog post and named as such by Jennifer Chayes. Kohlenbach’s general logical metatheorems of proof […]
30 May, 2021 at 1:11 am
Finitary proofs of Borel-Cantelli lemmas | Subin Pulari
[…] we explore the Borel-Cantelli lemmas from a hard analytic/finitary perspective. We obtain finitary analogues of these lemmas using elementary tail bounds from […]
3 March, 2022 at 7:26 pm
Mengingat jumlah monyet yang tidak terbatas dan waktu yang tidak terbatas, apakah salah satu dari mereka akan menulis Hamlet? - Pripun?net
[…] adalah contoh dari Jenderal “analisis lunak ke analisis kerasPrinsip yang diperjuangkan oleh Terry Tao antara lain: hampir semua bukti dalam analisis dapat […]
13 November, 2022 at 9:21 am
Numerical constants are not a red flag – some compact thoughts
[…] proof, because let’s be honest, nobody else commenting on the proof, other than experts in hard analytic number theory, has any chance of understanding the proof either. And since Peking […]
24 April, 2024 at 7:03 am
Notes on the B+B+t theorem | What's new
[…] 1 is then equivalent to the following “almost finitary” version (cf. this previous discussion of almost finitary versions of the infinite pigeonhole […]