You are currently browsing the category archive for the ‘opinion’ category.
This is a somewhat experimental and speculative post. This week I was at the IPAM workshop on machine assisted proof that I was one of the organizers of. We had an interesting and diverse range of talks, both from computer scientists presenting the latest available tools to formally verify proofs or to automate various aspects of proof writing or proof discovery, as well as mathematicians who described their experiences using these tools to solve their research problems. One can find the videos of these talks on the IPAM youtube channel; I also posted about the talks during the event on my Mathstodon account. I am of course not the most objective person to judge, but from the feedback I received it seems that the conference was able to successfully achieve its aim of bringing together the different communities interested in this topic.
As a result of the conference I started thinking about what possible computer tools might now be developed that could be of broad use to mathematicians, particularly those who do not have prior expertise with the finer aspects of writing code or installing software. One idea that came to mind was a potential tool to could take, say, an arXiv preprint as input, and return some sort of diagram detailing the logical flow of the main theorems and lemmas in the paper. This is currently done by hand by authors in some, but not all, papers (and can often also be automatically generated from formally verified proofs, as seen for instance in the graphic accompanying the IPAM workshop, or this diagram generated from Massot’s blueprint software from a manually inputted set of theorems and dependencies as a precursor to formalization of a proof [thanks to Thomas Bloom for this example]). For instance, here is a diagram that my co-author Rachel Greenfeld and I drew for a recent paper:
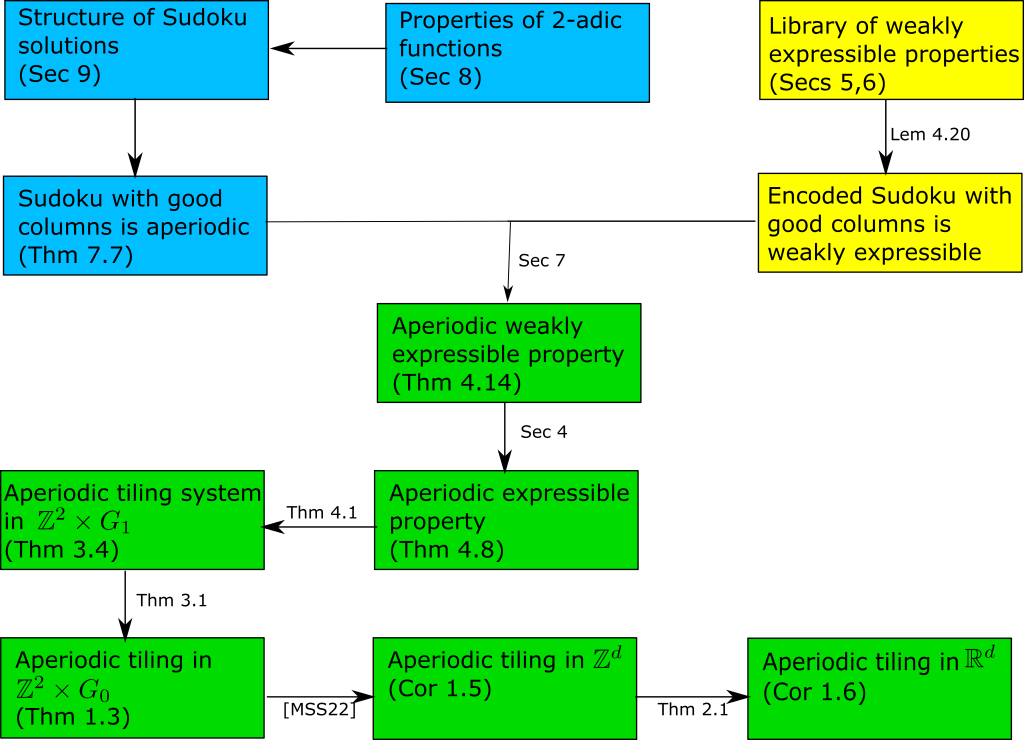
This particular diagram incorporated a number of subjective design choices regarding layout, which results to be designated important enough to require a dedicated box (as opposed to being viewed as a mere tool to get from one box to another), and how to describe each of these results (and how to colour-code them). This is still a very human-intensive task (and my co-author and I went through several iterations of this particular diagram with much back-and-forth discussion until we were both satisfied). But I could see the possibility of creating an automatic tool that could provide an initial “first approximation” to such a diagram, which a human user could then modify as they see fit (perhaps using some convenient GUI interface, for instance some variant of the Quiver online tool for drawing commutative diagrams in LaTeX).
As a crude first attempt at automatically generating such a diagram, one couuld perhaps develop a tool to scrape a LaTeX file to locate all the instances of the theorem environment in the text (i.e., all the formally identified lemmas, corollaries, and so forth), and for each such theorem, locate a proof environment instance that looks like it is associated to that theorem (doing this with reasonable accuracy may require a small amount of machine learning, though perhaps one could just hope that proximity of the proof environment instance to the theorem environment instance suffices in many cases). Then identify all the references within that proof environment to other theorems to start building the tree of implications, which one could then depict in a diagram such as the above. Such an approach would likely miss many of the implications; for instance, because many lemmas might not be proven using a formal proof environment, but instead by some more free-flowing text discussion, or perhaps a one line justification such as “By combining Lemma 3.4 and Proposition 3.6, we conclude”. Also, some references to other results in the paper might not proceed by direct citation, but by more indirect justifications such as “invoking the previous lemma, we obtain” or “by repeating the arguments in Section 3, we have”. Still, even such a crude diagram might still be helpful, both as a starting point for authors to make an improved diagram, or for a student trying to understand a lengthy paper to get some initial idea of the logical structure.
More advanced features might be to try to use more of the text of the paper to assign some measure of importance to individual results (and then weight the diagram correspondingly to highlight the more important results), to try to give each result a natural language description, and to somehow capture key statements that are not neatly encapsulated in a theorem environment instance, but I would imagine that such tasks should be deferred until some cruder proof-of-concept prototype can be demonstrated.
Anyway, I would be interested to hear opinions about whether this idea (or some modification thereof) is (a) actually feasible with current technology (or better yet, already exists in some form), and (b) of interest to research mathematicians.
[This post is collectively authored by the ICM structure committee, whom I am currently chairing – T.]
The ICM structure committee is responsible for the preparation of the Scientific Program of the International Congress of Mathematicians (ICM). It decides the structure of the Scientific Program, in particular,
- the number of plenary lectures,
- the sections and their precise definition,
- the target number of talks in each section,
- other kind of lectures, and
- the arrangement of sections.
(The actual selection of speakers and the local organization of the ICM are handled separately by the Program Committee and Organizing Comittee respectively.)
Our committee can also propose more radical changes to the format of the congress, although certain components of the congress, such as the prize lectures and satellite events, are outside the jurisdiction of this committee. For instance, in 2019 we proposed the addition of two new categories of lectures, “special sectional lectures” and “special plenary lectures”, which are broad and experimental categories of lectures that do not fall under the traditional format of a mathematician presenting their recent advances in a given section, but can instead highlight (for instance) emerging connections between two areas of mathematics, or present a “big picture” talk on a “hot topic” from an expert with the appropriate perspective. These new categories made their debut at the recently concluded virtual ICM, held on July 6-14, 2022.
Over the next year or so, our committee will conduct our deliberations on proposed changes to the structure of the congress for the next ICM (to be held in-person in Philadelphia in 2026) and beyond. As part of the preparation for these deliberations, we are soliciting feedback from the general mathematics community (on this blog and elsewhere) on the current state of the ICM, and any proposals to improve that state for the subsequent congresses; we had issued a similar call on this blog back in 2019. This time around, of course, the situation is complicated by the extraordinary and exceptional circumstances that led to the 2022 ICM being moved to a virtual platform on short notice, and so it is difficult for many reasons to hold the 2022 virtual ICM as a model for subsequent congresses. On the other hand, the scientific program had already been selected by the 2022 ICM Program Committee prior to the invasion of Ukraine, and feedback on the content of that program will be of great value to our committee.
Among the specific questions (in no particular order) for which we seek comments are the following:
- Are there suggestions to change the format of the ICM that would increase its value to the mathematical community?
- Are there suggestions to change the format of the ICM that would encourage greater participation and interest in attending, particularly with regards to junior researchers and mathematicians from developing countries?
- The special sectional and special plenary lectures were introduced in part to increase the emphasis on the quality of exposition at ICM lectures. Has this in fact resulted in a notable improvement in exposition, and should any alternations be made to the special lecture component of the ICM?
- Is the balance between plenary talks, sectional talks, special plenary and sectional talks, and public talks at an optimal level? There is only a finite amount of space in the calendar, so any increase in the number or length of one of these types of talks will come at the expense of another.
- The ICM is generally perceived to be more important to pure mathematics than to applied mathematics. In what ways can the ICM be made more relevant and attractive to applied mathematicians, or should one not try to do so?
- Are there structural barriers that cause certain areas or styles of mathematics (such as applied or interdisciplinary mathematics) or certain groups of mathematicians to be under-represented at the ICM? What, if anything, can be done to mitigate these barriers?
- The recently concluded virtual ICM had a sui generis format, in which the core virtual program was supplemented by a number of physical “overlay” satellite events. Are there any positive features of that format which could potentially be usefully adapted to such congresses? For instance, should there be any virtual or hybrid components at the next ICM?
Of course, we do not expect these complex and difficult questions to be resolved within this blog post, and debating these and other issues would likely be a major component of our internal committee discussions. Nevertheless, we would value constructive comments towards the above questions (or on other topics within the scope of our committee) to help inform these subsequent discussions. We therefore welcome and invite such commentary, either as responses to this blog post, or sent privately to one of the members of our committee. We would also be interested in having readers share their personal experiences at past congresses, and how it compares with other major conferences of this type. (But in order to keep the discussion focused and constructive, we request that comments here refrain from discussing topics that are out of the scope of this committee, such as suggesting specific potential speakers for the next congress, which is a task instead for the 2022 ICM Program Committee. Comments that are specific to the recently concluded virtual ICM can be made instead at this blog post.)
[Note: while I am chair of the ICM Structure Committee, this blog post is not an official request from this committee, as events are still moving too rapidly to proceed at present via normal committee deliberations. We are however discussing these matters and may issue a more formal request in due course. -T.]
The International Mathematical Union has just made the following announcement concerning the International Congress of Mathematicians (ICM) that was previously scheduled to be held in St. Petersburg, Russia in July.
Decision of the Executive Committee of the IMU on the upcoming ICM 2022 and IMU General Assembly
On 26 February 2022, the Executive Committee of the International Mathematical Union (IMU) decided that:
1. The International Congress of Mathematicians (ICM) 2022 will take place as a fully virtual event, hosted outside Russia but following the original time schedule planned for Saint Petersburg.
2. Participation in the virtual ICM event will be free of charge.
3. The IMU General Assembly (GA) will take place as an in-person event outside Russia.
4. A prize ceremony will be held the day after the IMU GA, at the same venue as the IMU GA, for the awarding of the 2022 IMU prizes.
5. The dates for the ICM and the GA will remain unaltered.
6. We will return with further practical information regarding the two events.
An expanded version of the announcement can be found here. (See also this addendum.)
While I am not on the IMU Executive Committee and thus not privy to their deliberations, I have been in contact with several members of this committee and I support their final decision on these matters.
As we have all experienced during the COVID-19 pandemic, virtual conferences can be rather variable in quality, but there certainly are ways to make the experience more positive for both the speakers and participants. In the interest of maximizing the benefits that this meeting can still produce, I would like to invite readers of this blog to share any experiences they have had with very large virtual conferences, and any opinions on what types of virtual events were effective and engaging.
One idea that has been suggested to me has been to have (either unofficial, semi-official, or official) regional ICM hosting events at various places worldwide where mathematicians could gather in person to view ICM talks that would be streamed online (and perhaps some ICM speakers from that area could give talks in person in such locations). This would be very nonstandard, of course, but could be one way to salvage some of the physical ICM experience, and perhaps also a way to symbolically support the spirit of the Congress. I would be interested to get some feedback on this proposal.
Finally, I would like to request that comments to this post remain focused on the upcoming virtual ICM. Broader political issues are very much worth discussing at present, but there are other venues for such discussion, and as per my usual blog policy any off-topic comments may be subject to deletion.
[The following statement is signed by several mathematicians at Stanford and MIT in support of one of their recently admitted graduate students, and I am happy to post it here on my blog. -T]
We were saddened and horrified to learn that Ilya Dumanski, a brilliant young mathematician who has been admitted to our graduate programs at Stanford and MIT, has been imprisoned in Russia, along with several other mathematicians, for participation in a peaceful demonstration. Our thoughts are with them. We urge their rapid release, and failing that, that they be kept in humane conditions. A petition in their support has been started at
https://www.ipetitions.com/petition/a-call-for-immediate-release-of-arrested-students/
Signed,
Roman Bezrukavnikov (MIT)
Alexei Borodin (MIT)
Daniel Bump (Stanford)
Sourav Chatterjee (Stanford)
Otis Chodosh (Stanford)
Ralph Cohen (Stanford)
Henry Cohn (MIT)
Brian Conrad (Stanford)
Joern Dunkel (MIT)
Pavel Etingof (MIT)
Jacob Fox (Stanford)
Michel Goemans (MIT)
Eleny Ionel (Stanford)
Steven Kerckhoff (Stanford)
Jonathan Luk (Stanford)
Eugenia Malinnikova (Stanford)
Davesh Maulik (MIT)
Rafe Mazzeo (Stanford)
Haynes Miller (MIT)
Ankur Moitra (MIT)
Elchanan Mossel (MIT)
Tomasz Mrowka (MIT)
Bjorn Poonen (MIT)
Alex Postnikov (MIT)
Lenya Ryzhik (Stanford)
Paul Seidel (MIT)
Mike Sipser (MIT)
Kannan Soundararajan (Stanford)
Gigliola Staffilani (MIT)
Nike Sun (MIT)
Richard Taylor (Stanford)
Ravi Vakil (Stanford)
Andras Vasy (Stanford)
Jan Vondrak (Stanford)
Brian White (Stanford)
Zhiwei Yun (MIT)
In the last week or so there has been some discussion on the internet about a paper (initially authored by Hill and Tabachnikov) that was initially accepted for publication in the Mathematical Intelligencer, but with the editor-in-chief of that journal later deciding against publication; the paper, in significantly revised form (and now authored solely by Hill), was then quickly accepted by one of the editors in the New York Journal of Mathematics, but then was removed from publication after objections from several members on the editorial board of NYJM that the paper had not been properly refereed or was within the scope of the journal; see this statement by Benson Farb, who at the time was on that board, for more details. Some further discussion of this incident may be found on Tim Gowers’ blog; the most recent version of the paper, as well as a number of prior revisions, are still available on the arXiv here.
For whatever reason, some of the discussion online has focused on the role of Amie Wilkinson, a mathematician from the University of Chicago (and who, incidentally, was a recent speaker here at UCLA in our Distinguished Lecture Series), who wrote an email to the editor-in-chief of the Intelligencer raising some concerns about the content of the paper and suggesting that it be published alongside commentary from other experts in the field. (This, by the way, is not uncommon practice when dealing with a potentially provocative publication in one field by authors coming from a different field; for instance, when Emmanuel Candès and I published a paper in the Annals of Statistics introducing what we called the “Dantzig selector”, the Annals solicited a number of articles discussing the selector from prominent statisticians, and then invited us to submit a rejoinder.) It seems that the editors of the Intelligencer decided instead to reject the paper. The paper then had a complicated interaction with NYJM, but, as stated by Wilkinson in her recent statement on this matter as well as by Farb, this was done without any involvement from Wilkinson. (It is true that Farb happens to also be Wilkinson’s husband, but I see no reason to doubt their statements on this matter.)
I have not interacted much with the Intelligencer, but I have published a few papers with NYJM over the years; it is an early example of a quality “diamond open access” mathematics journal. It seems that this incident may have uncovered some issues with their editorial procedure for reviewing and accepting papers, but I am hopeful that they can be addressed to avoid this sort of event occurring again.
The self-chosen remit of my blog is “Updates on my research and expository papers, discussion of open problems, and other maths-related topics”. Of the 774 posts on this blog, I estimate that about 99% of the posts indeed relate to mathematics, mathematicians, or the administration of this mathematical blog, and only about 1% are not related to mathematics or the community of mathematicians in any significant fashion.
This is not one of the 1%.
Mathematical research is clearly an international activity. But actually a stronger claim is true: mathematical research is a transnational activity, in that the specific nationality of individual members of a research team or research community are (or should be) of no appreciable significance for the purpose of advancing mathematics. For instance, even during the height of the Cold War, there was no movement in (say) the United States to boycott Soviet mathematicians or theorems, or to only use results from Western literature (though the latter did sometimes happen by default, due to the limited avenues of information exchange between East and West, and former did occasionally occur for political reasons, most notably with the Soviet Union preventing Gregory Margulis from traveling to receive his Fields Medal in 1978 EDIT: and also Sergei Novikov in 1970). The national origin of even the most fundamental components of mathematics, whether it be the geometry (γεωμετρία) of the ancient Greeks, the algebra (الجبر) of the Islamic world, or the Hindu-Arabic numerals 
Of course, mathematicians cannot ignore the political realities of the modern international order altogether. Anyone who has organised an international conference or program knows that there will inevitably be visa issues to resolve because the host country makes it particularly difficult for certain nationals to attend the event. I myself, like many other academics working long-term in the United States, have certainly experienced my own share of immigration bureaucracy, starting with various glitches in the renewal or application of my J-1 and O-1 visas, then to the lengthy vetting process for acquiring permanent residency (or “green card”) status, and finally to becoming naturalised as a US citizen (retaining dual citizenship with Australia). Nevertheless, while the process could be slow and frustrating, there was at least an order to it. The rules of the game were complicated, but were known in advance, and did not abruptly change in the middle of playing it (save in truly exceptional situations, such as the days after the September 11 terrorist attacks). One just had to study the relevant visa regulations (or hire an immigration lawyer to do so), fill out the paperwork and submit to the relevant background checks, and remain in good standing until the application was approved in order to study, work, or participate in a mathematical activity held in another country. On rare occasion, some senior university administrator may have had to contact a high-ranking government official to approve some particularly complicated application, but for the most part one could work through normal channels in order to ensure for instance that the majority of participants of a conference could actually be physically present at that conference, or that an excellent mathematician hired by unanimous consent by a mathematics department could in fact legally work in that department.
With the recent and highly publicised executive order on immigration, many of these fundamental assumptions have been seriously damaged, if not destroyed altogether. Even if the order was withdrawn immediately, there is no longer an assurance, even for nationals not initially impacted by that order, that some similar abrupt and major change in the rules for entry to the United States could not occur, for instance for a visitor who has already gone through the lengthy visa application process and background checks, secured the appropriate visa, and is already in flight to the country. This is already affecting upcoming or ongoing mathematical conferences or programs in the US, with many international speakers (including those from countries not directly affected by the order) now cancelling their visit, either in protest or in concern about their ability to freely enter and leave the country. Even some conferences outside the US are affected, as some mathematicians currently in the US with a valid visa or even permanent residency are uncertain if they could ever return back to their place of work if they left the country to attend a meeting. In the slightly longer term, it is likely that the ability of elite US institutions to attract the best students and faculty will be seriously impacted. Again, the losses would be strongest regarding candidates that were nationals of the countries affected by the current executive order, but I fear that many other mathematicians from other countries would now be much more concerned about entering and living in the US than they would have previously.
It is still possible for this sort of long-term damage to the mathematical community (both within the US and abroad) to be reversed or at least contained, but at present there is a real risk of the damage becoming permanent. To prevent this, it seems insufficient for me for the current order to be rescinded, as desirable as that would be; some further legislative or judicial action would be needed to begin restoring enough trust in the stability of the US immigration and visa system that the international travel that is so necessary to modern mathematical research becomes “just” a bureaucratic headache again.
Of course, the impact of this executive order is far, far broader than just its effect on mathematicians and mathematical research. But there are countless other venues on the internet and elsewhere to discuss these other aspects (or politics in general). (For instance, discussion of the qualifications, or lack thereof, of the current US president can be carried out at this previous post.) I would therefore like to open this post to readers to discuss the effects or potential effects of this order on the mathematical community; I particularly encourage mathematicians who have been personally affected by this order to share their experiences. As per the rules of the blog, I request that “the discussions are kept constructive, polite, and at least tangentially relevant to the topic at hand”.
Some relevant links (please feel free to suggest more, either through comments or by email):
- AMS Board of Trustees opposes executive order on immigration
- MAA Executive Committee Statement on Immigration Ban
- SIAM responds to White House Executive Order on Visas and Immigration
- Multisociety letter on immigration
- EMS President on Trump’s Executive Order
- International Council for Science (ICSU) calls on the government of the United States to rescind the Executive Order “Protecting the Nation from Foreign Terrorist Entry into the United States”
- Public Universities Respond to New Immigration Order
- Statement from the Association for Women in Mathematics
- Simons Foundation Statement on Executive Order on Visas and Immigration
- A letter from the editors of the AMS graduate student blog on the Executive Order on Immigration
- Statement of inclusiveness (a petition, primarily aimed at mathematicians, created and hosted by Kasra Rafi and Juan Souto)
- Academics Against Executive Immigration Order (a petition, aimed at the broader academic community)
- First they came for the Iranians, blog post, Scott Aaronson
- IAS statement on the revised executive order
- The immigration ban is still antithetical to scientific progress, blog post, Boaz Barak and Omer Reingold
In logic, there is a subtle but important distinction between the concept of mutual knowledge – information that everyone (or almost everyone) knows – and common knowledge, which is not only knowledge that (almost) everyone knows, but something that (almost) everyone knows that everyone else knows (and that everyone knows that everyone else knows that everyone else knows, and so forth). A classic example arises from Hans Christian Andersens’ fable of the Emperor’s New Clothes: the fact that the emperor in fact has no clothes is mutual knowledge, but not common knowledge, because everyone (save, eventually, for a small child) is refusing to acknowledge the emperor’s nakedness, thus perpetuating the charade that the emperor is actually wearing some incredibly expensive and special clothing that is only visible to a select few. My own personal favourite example of the distinction comes from the blue-eyed islander puzzle, discussed previously here, here and here on the blog. (By the way, I would ask that any commentary about that puzzle be directed to those blog posts, rather than to the current one.)
I believe that there is now a real-life instance of this situation in the US presidential election, regarding the following
Proposition 1. The presumptive nominee of the Republican Party, Donald Trump, is not even remotely qualified to carry out the duties of the presidency of the United States of America.
Proposition 1 is a statement which I think is approaching the level of mutual knowledge amongst the US population (and probably a large proportion of people following US politics overseas): even many of Trump’s nominal supporters secretly suspect that this proposition is true, even if they are hesitant to say it out loud. And there have been many prominent people, from both major parties, that have made the case for Proposition 1: for instance Mitt Romney, the Republican presidential nominee in 2012, did so back in March, and just a few days ago Hillary Clinton, the likely Democratic presidential nominee this year, did so in this speech:
I highly recommend watching the entirety of the (35 mins or so) speech, followed by the entirety of Trump’s rebuttal.
However, even if Proposition 1 is approaching the status of “mutual knowledge”, it does not yet seem to be close to the status of “common knowledge”: one may secretly believe that Trump cannot be considered as a serious candidate for the US presidency, but must continue to entertain this possibility, because they feel that others around them, or in politics or the media, appear to be doing so. To reconcile these views can require taking on some implausible hypotheses that are not otherwise supported by any evidence, such as the hypothesis that Trump’s displays of policy ignorance, pettiness, and other clearly unpresidential behaviour are merely “for show”, and that behind this facade there is actually a competent and qualified presidential candidate; much like the emperor’s new clothes, this alleged competence is supposedly only visible to a select few. And so the charade continues.
I feel that it is time for the charade to end: Trump is unfit to be president, and everybody knows it. But more people need to say so, openly.
Important note: I anticipate there will be any number of “tu quoque” responses, asserting for instance that Hillary Clinton is also unfit to be the US president. I personally do not believe that to be the case (and certainly not to the extent that Trump exhibits), but in any event such an assertion has no logical bearing on the qualification of Trump for the presidency. As such, any comments that are purely of this “tu quoque” nature, and which do not directly address the validity or epistemological status of Proposition 1, will be deleted as off-topic. However, there is a legitimate case to be made that there is a fundamental weakness in the current mechanics of the US presidential election, particularly with the “first-past-the-post” voting system, in that (once the presidential primaries are concluded) a voter in the presidential election is effectively limited to choosing between just two viable choices, one from each of the two major parties, or else refusing to vote or making a largely symbolic protest vote. This weakness is particularly evident when at least one of these two major choices is demonstrably unfit for office, as per Proposition 1. I think there is a serious case for debating the possibility of major electoral reform in the US (I am particularly partial to the Instant Runoff Voting system, used for instance in my home country of Australia, which allows for meaningful votes to third parties), and I would consider such a debate to be on-topic for this post. But this is very much a longer term issue, as there is absolutely no chance that any such reform would be implemented by the time of the US elections in November (particularly given that any significant reform would almost certainly require, at minimum, a constitutional amendment).
It has been a little over two weeks now since the protest site at thecostofknowledge.com was set up to register declarations of non-cooperation with Reed Elsevier in protest of their research publishing practices, inspired by this blog post of Tim Gowers. Awareness of the protest has certainly grown in these two weeks; the number of signatories is now well over four thousand, across a broad array of academic disciplines, and the protest has been covered by many blogs and also the mainstream media (e.g. the Guardian, the Economist, Forbes, etc.), and even by Elsevier stock analysts. (Elsevier itself released an open letter responding to the protest here.) My interpretation of events is that there was a significant amount of latent or otherwise undisclosed dissatisfaction already with the publishing practices of Elsevier (and, to a lesser extent, some other commercial academic publishers), and a desire to support alternatives such as university or society publishers, and the more recent open access journals; and that this protest (and parallel protests, such as the movement to oppose the Research Works Act) served to drive these feelings out into the open.
The statement of the protest itself, though, is rather brief, reflecting the improvised manner in which the site was created. A group of mathematicians including myself therefore decided to write and sign a more detailed explanation of why we supported this protest, giving more background and references to support our position. The 34 signatories are Scott Aaronson, Douglas N. Arnold, Artur Avila, John Baez, Folkmar Bornemann, Danny Calegari, Henry Cohn, Ingrid Daubechies, Jordan Ellenberg, Matthew Emerton, Marie Farge, David Gabai, Timothy Gowers, Ben Green, Martin Grotschel, Michael Harris, Frederic Helein, Rob Kirby, Vincent Lafforgue, Gregory F. Lawler, Randall J. LeVeque, Laszlo Lovasz, Peter J. Olver, Olof Sisask, Richard Taylor, Bernard Teissier, Burt Totaro, Lloyd N. Trefethen, Takashi Tsuboi, Marie-France Vigneras, Wendelin Werner, Amie Wilkinson, Gunter M. Ziegler, and myself. (Note that while Daubechies is current president of the International Mathematical Union, Lovasz is a past president, and Grotschel is the current secretary, they are signing this letter as individuals and not as representatives of the IMU. Similarly for Trefethen and Arnold (current and past president of SIAM).)
Of course, the 34 of us do not presume to speak for the remaining four thousand signatories to the protest, but I hope that our statement is somewhat representative of the position of many of its supporters.
Further discussion of this statement can be found at this blog post of Tim Gowers.
EDIT: I think it is appropriate to quote the following excerpt from our statement:
All mathematicians must decide for themselves whether, or to what extent, they wish to participate in the boycott. Senior mathematicians who have signed the boycott bear some responsibility towards junior colleagues who are forgoing the option of publishing in Elsevier journals, and should do their best to help minimize any negative career consequences.
Whether or not you decide to join the boycott, there are some simple actions that everyone can take, which seem to us to be uncontroversial:
- Make sure that the final versions of all your papers, particularly new ones, are freely available online, ideally both on the arXiv and on your home page.
- If you are submitting a paper and there is a choice between an expensive journal and a cheap (or free) journal of the same standard, then always submit to the cheap one.
A few days ago, inspired by this recent post of Tim Gowers, a web page entitled “the cost of knowledge” has been set up as a location for mathematicians and other academics to declare a protest against the academic publishing practices of Reed Elsevier, in particular with regard to their exceptionally high journal prices, their policy of “bundling” journals together so that libraries are forced to purchase subscriptions to large numbers of low-quality journals in order to gain access to a handful of high-quality journals, and their opposition to the open access movement (as manifested, for instance, in their lobbying in support of legislation such as the Stop Online Piracy Act (SOPA) and the Research Works Act (RWA)). [These practices have been documented in a number of places; this wiki page, which was set up in response to Tim’s post, collects several relevant links for this purpose. Some of the other commercial publishers have exhibited similar behaviour, though usually not to the extent that Elsevier has, which is why this particular publisher is the focus of this protest.] At the protest site, one can publicly declare a refusal to either publish at an Elsevier journal, referee for an Elsevier journal, or join the board of an Elsevier journal.
(In the past, the editorial boards of several Elsevier journals have resigned over the pricing policies of the journal, most famously the board of Topology in 2006, but also the Journal of Algorithms in 2003, and a number of journals in other sciences as well. Several libraries, such as those of Harvard and Cornell, have also managed to negotiate an unbundling of Elsevier journals, but most libraries are still unable to subscribe to such journals individually.)
For a more thorough discussion as to why such a protest is warranted, please see Tim’s post on the matter (and the 100+ comments to that post). Many of the issues regarding Elsevier were already known to some extent to many mathematicians (particularly those who have served on departmental library committees), several of whom had already privately made the decision to boycott Elsevier; but nevertheless it is important to bring these issues out into the open, to make them commonly known as opposed to merely mutually known. (Amusingly, this distinction is also of crucial importance in my favorite logic puzzle, but that’s another story.) One can also see Elsevier’s side of the story in this response to Tim’s post by David Clark (the Senior Vice President for Physical Sciences at Elsevier).
For my own part, though I have sent about 9% of my papers in the past to Elsevier journals (with one or two still in press), I have now elected not to submit any further papers to these journals, nor to serve on their editorial boards, though I will continue refereeing some papers from these journals. As of this time of writing, over five hundred mathematicians and other academics have also signed on to the protest in the four days that the site has been active.
Admittedly, I am fortunate enough to be at a stage of career in which I am not pressured to publish in a very specific set of journals, and as such, I am not making a recommendation as to what anyone else should do or not do regarding this protest. However, I do feel that it is worth spreading awareness, at least, of the fact that such protests exist (and some additional petitions on related issues can be found at the previously mentioned wiki page).
A friend of mine recently asked me for some suggestions for games or other activities for children that would help promote quantitative reasoning or mathematical skills, while remaining fun to play (i.e. more than just homework-type questions poorly disguised in game form). The initial question was focused on computer games (and specifically, on iPhone apps), but I think the broader question would also be of interest.
I myself have not seriously played these sorts of games for years, so I could only come up with a few examples immediately: the game “Planarity“, and the game “Factory Balls” (and two sequels). (Edit: Rubik’s cube and its countless cousins presumably qualify also, due to their implicit use of group theory.) I am hopeful though that readers may be able to come up with more suggestions.
There is of course no shortage of “educational” games, computer-based or otherwise, available, but I think what I (and my friend) would be looking for here are games with production values comparable to other, less educational games, and for which the need for mathematical thinking arises naturally in the gameplay rather than being artificially inserted by fiat (e.g. “solve this equation to proceed”). (Here I interpret “mathematical thinking” loosely, to include not just numerical or algebraic thinking, but also geometric, abstract, logical, probabilistic, etc.)
[Question for MathOverflow experts: would this type of question be suitable for crossposting there? The requirement that such questions be “research-level” seems to suggest not.]
What's new 
Recent Comments