Uhlenbeck’s theorem on connections with small curvature

I was pleased to learn this week that the 2019 Abel Prize was awarded to Karen Uhlenbeck. Uhlenbeck laid much of the foundations of modern geometric PDE. One of the few papers I have in this area is in fact a joint paper with Gang Tian extending a famous singularity removal theorem of Uhlenbeck for four-dimensional Yang-Mills connections to higher dimensions. In both these papers, it is crucial to be able to construct “Coulomb gauges” for various connections, and there is a clever trick of Uhlenbeck for doing so, introduced in another important paper of hers, which is absolutely critical in my own paper with Tian. Nowadays it would be considered a standard technique, but it was definitely not so at the time that Uhlenbeck introduced it.

Suppose one has a smooth connection on a (closed) unit ball in for some , taking values in some Lie algebra associated to a compact Lie group . This connection then has a curvature , defined in coordinates by the usual formula

It is natural to place the curvature in a scale-invariant space such as , and then the natural space for the connection would be the Sobolev space . It is easy to see from (1) and Sobolev embedding that if is bounded in , then will be bounded in . One can then ask the converse question: if is bounded in , is bounded in ? This can be viewed as asking whether the curvature equation (1) enjoys “elliptic regularity”.

There is a basic obstruction provided by gauge invariance. For any smooth gauge taking values in the Lie group, one can gauge transform to

and then a brief calculation shows that the curvature is conjugated to

This gauge symmetry does not affect the norm of the curvature tensor , but can make the connection extremely large in , since there is no control on how wildly can oscillate in space.

However, one can hope to overcome this problem by gauge fixing: perhaps if is bounded in , then one can make bounded in after applying a gauge transformation. The basic and useful result of Uhlenbeck is that this can be done if the norm of is sufficiently small (and then the conclusion is that is small in ). (For large connections there is a serious issue related to the Gribov ambiguity.) In my (much) later paper with Tian, we adapted this argument, replacing Lebesgue spaces by Morrey space counterparts. (This result was also independently obtained at about the same time by Meyer and Riviére.)

To make the problem elliptic, one can try to impose the Coulomb gauge condition

(also known as the Lorenz gauge or Hodge gauge in various papers), together with a natural boundary condition on that will not be discussed further here. This turns (1), (2) into a divergence-curl system that is elliptic at the linear level at least. Indeed if one takes the divergence of (1) using (2) one sees that

and if one could somehow ignore the nonlinear term then we would get the required regularity on by standard elliptic regularity estimates.

The problem is then how to handle the nonlinear term. If we already knew that was small in the right norm then one can use Sobolev embedding, Hölder’s inequality, and elliptic regularity to show that the second term in (3) is small compared to the first term, and so one could then hope to eliminate it by perturbative analysis. However, proving that is small in this norm is exactly what we are trying to prove! So this approach seems circular.

Uhlenbeck’s clever way out of this circularity is a textbook example of what is now known as a “continuity” argument. Instead of trying to work just with the original connection , one works with the rescaled connections for , with associated rescaled curvatures . If the original curvature is small in norm (e.g. bounded by some small ), then so are all the rescaled curvatures . We want to obtain a Coulomb gauge at time ; this is difficult to do directly, but it is trivial to obtain a Coulomb gauge at time , because the connection vanishes at this time. On the other hand, once one has successfully obtained a Coulomb gauge at some time with small in the natural norm (say bounded by for some constant which is large in absolute terms, but not so large compared with say ), the perturbative argument mentioned earlier (combined with the qualitative hypothesis that is smooth) actually works to show that a Coulomb gauge can also be constructed and be small for all sufficiently close nearby times to ; furthermore, the perturbative analysis actually shows that the nearby gauges enjoy a slightly better bound on the norm, say rather than . As a consequence of this, the set of times for which one has a good Coulomb gauge obeying the claimed estimates is both open and closed in , and also contains . Since the unit interval is connected, it must then also contain . This concludes the proof.

One of the lessons I drew from this example is to not be deterred (especially in PDE) by an argument seeming to be circular; if the argument is still sufficiently “nontrivial” in nature, it can often be modified into a usefully non-circular argument that achieves what one wants (possibly under an additional qualitative hypothesis, such as a continuity or smoothness hypothesis).

Prismatic cohomology

Last week, we had Peter Scholze give an interesting distinguished lecture series here at UCLA on “Prismatic Cohomology”, which is a new type of cohomology theory worked out by Scholze and Bhargav Bhatt. (Video of the talks will be available shortly; for now we have some notes taken by two note–takers in the audience on that web page.) My understanding of this (speaking as someone that is rather far removed from this area) is that it is progress towards the “motivic” dream of being able to define cohomology for varieties (or similar objects) defined over arbitrary commutative rings , and with coefficients in another arbitrary commutative ring . Currently, we have various flavours of cohomology that only work for certain types of domain rings and coefficient rings :

• Singular cohomology, which roughly speaking works when the domain ring is a characteristic zero field such as or , but can allow for arbitrary coefficients ;
• de Rham cohomology, which roughly speaking works as long as the coefficient ring is the same as the domain ring (or a homomorphic image thereof), as one can only talk about -valued differential forms if the underlying space is also defined over ;
• -adic cohomology, which is a remarkably powerful application of étale cohomology, but only works well when the coefficient ring is localised around a prime that is different from the characteristic of the domain ring ; and
• Crystalline cohomology, in which the domain ring is a field of some finite characteristic , but the coefficient ring can be a slight deformation of , such as the ring of Witt vectors of .

There are various relationships between the cohomology theories, for instance de Rham cohomology coincides with singular cohomology for smooth varieties in the limiting case . The following picture Scholze drew in his first lecture captures these sorts of relationships nicely:

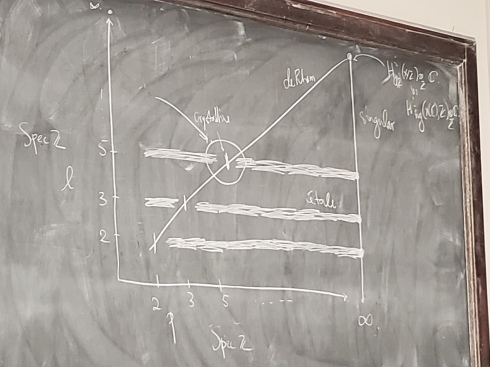
The new prismatic cohomology of Bhatt and Scholze unifies many of these cohomologies in the “neighbourhood” of the point in the above diagram, in which the domain ring and the coefficient ring are both thought of as being “close to characteristic ” in some sense, so that the dilates of these rings is either zero, or “small”. For instance, the -adic ring is technically of characteristic , but is a “small” ideal of (it consists of those elements of of -adic valuation at most ), so one can think of as being “close to characteristic ” in some sense. Scholze drew a “zoomed in” version of the previous diagram to informally describe the types of rings for which prismatic cohomology is effective:

To define prismatic cohomology rings one needs a “prism”: a ring homomorphism from to equipped with a “Frobenius-like” endomorphism on obeying some axioms. By tuning these homomorphisms one can recover existing cohomology theories like crystalline or de Rham cohomology as special cases of prismatic cohomology. These specialisations are analogous to how a prism splits white light into various individual colours, giving rise to the terminology “prismatic”, and depicted by this further diagram of Scholze:

(And yes, Peter confirmed that he and Bhargav were inspired by the Dark Side of the Moon album cover in selecting the terminology.)

There was an abstract definition of prismatic cohomology (as being the essentially unique cohomology arising from prisms that obeyed certain natural axioms), but there was also a more concrete way to view them in terms of coordinates, as a “-deformation” of de Rham cohomology. Whereas in de Rham cohomology one worked with derivative operators that for instance applied to monomials by the usual formula

prismatic cohomology in coordinates can be computed using a “-derivative” operator that for instance applies to monomials by the formula

where

is the “-analogue” of (a polynomial in that equals in the limit ). (The -analogues become more complicated for more general forms than these.) In this more concrete setting, the fact that prismatic cohomology is independent of the choice of coordinates apparently becomes quite a non-trivial theorem.