Measurable tilings by abelian group actions

Jan Grebik, Rachel Greenfeld, Vaclav Rozhon and I have just uploaded to the arXiv our preprint “Measurable tilings by abelian group actions“. This paper is related to an earlier paper of Rachel Greenfeld and myself concerning tilings of lattices , but now we consider the more general situation of tiling a measure space by a tile shifted by a finite subset of shifts of an abelian group that acts in a measure-preserving (or at least quasi-measure-preserving) fashion on . For instance, could be a torus , could be a positive measure subset of that torus, and could be the group , acting on by translation.

If is a finite subset of with the property that the translates , of partition up to null sets, we write , and refer to this as a measurable tiling of by (with tiling set ). For instance, if is the torus , we can create a measurable tiling with and . Our main results are the following:

• By modifying arguments from previous papers (including the one with Greenfeld mentioned above), we can establish the following “dilation lemma”: a measurable tiling automatically implies further measurable tilings , whenever is an integer coprime to all primes up to the cardinality of .
• By averaging the above dilation lemma, we can also establish a “structure theorem” that decomposes the indicator function of into components, each of which are invariant with respect to a certain shift in . We can establish this theorem in the case of measure-preserving actions on probability spaces via the ergodic theorem, but one can also generalize to other settings by using the device of “measurable medial means” (which relates to the concept of a universally measurable set).
• By applying this structure theorem, we can show that all measurable tilings of the one-dimensional torus are rational, in the sense that lies in a coset of the rationals . This answers a recent conjecture of Conley, Grebik, and Pikhurko; we also give an alternate proof of this conjecture using some previous results of Lagarias and Wang.
• For tilings of higher-dimensional tori, the tiling need not be rational. However, we can show that we can “slide” the tiling to be rational by giving each translate of a “velocity” , and for every time , the translates still form a partition of modulo null sets, and at time the tiling becomes rational. In particular, if a set can tile a torus in an irrational fashion, then it must also be able to tile the torus in a rational fashion.
• In the two-dimensional case one can arrange matters so that all the velocities are parallel. If we furthermore assume that the tile is connected, we can also show that the union of all the translates with a common velocity form a -invariant subset of the torus.
• Finally, we show that tilings of a finitely generated discrete group , with a finite group, cannot be constructed in a “local” fashion (we formalize this probabilistically using the notion of a “factor of iid process”) unless the tile is contained in a single coset of . (Nonabelian local tilings, for instance of the sphere by rotations, are of interest due to connections with the Banach-Tarski paradox; see the aforementioned paper of Conley, Grebik, and Pikhurko. Unfortunately, our methods seem to break down completely in the nonabelian case.)

Perfectly packing a square by squares of nearly harmonic sidelength

I’ve just uploaded to the arXiv my preprint “Perfectly packing a square by squares of nearly harmonic sidelength“. This paper concerns a variant of an old problem of Meir and Moser, who asks whether it is possible to perfectly pack squares of sidelength for into a single square or rectangle of area . (The following variant problem, also posed by Meir and Moser and discussed for instance in this MathOverflow post, is perhaps even more well known: is it possible to perfectly pack rectangles of dimensions for into a single square of area ?) For the purposes of this paper, rectangles and squares are understood to have sides parallel to the axes, and a packing is perfect if it partitions the region being packed up to sets of measure zero. As one partial result towards these problems, it was shown by Paulhus that squares of sidelength for can be packed (not quite perfectly) into a single rectangle of area , and rectangles of dimensions for can be packed (again not quite perfectly) into a single square of area . (Paulhus’s paper had some gaps in it, but these were subsequently repaired by Grzegorek and Januszewski.)

Another direction in which partial progress has been made is to consider instead the problem of packing squares of sidelength , perfectly into a square or rectangle of total area , for some fixed constant (this lower bound is needed to make the total area finite), with the aim being to get as close to as possible. Prior to this paper, the most recent advance in this direction was by Januszewski and Zielonka last year, who achieved such a packing in the range .

In this paper we are able to get arbitrarily close to (which turns out to be a “critical” value of this parameter), but at the expense of deleting the first few tiles:

Theorem 1 If , and is sufficiently large depending on , then one can pack squares of sidelength , perfectly into a square of area .

As in previous works, the general strategy is to execute a greedy algorithm, which can be described somewhat incompletely as follows.

• Step 1: Suppose that one has already managed to perfectly pack a square of area by squares of sidelength for , together with a further finite collection of rectangles with disjoint interiors. (Initially, we would have and , but these parameter will change over the course of the algorithm.)
• Step 2: Amongst all the rectangles in , locate the rectangle of the largest width (defined as the shorter of the two sidelengths of ).
• Step 3: Pack (as efficiently as one can) squares of sidelength for into for some , and decompose the portion of not covered by this packing into rectangles .
• Step 4: Replace by , replace by , and return to Step 1.

The main innovation of this paper is to perform Step 3 somewhat more efficiently than in previous papers.

The above algorithm can get stuck if one reaches a point where one has already packed squares of sidelength for , but that all remaining rectangles in have width less than , in which case there is no obvious way to fit in the next square. If we let and denote the width and height of these rectangles , then the total area of the rectangles must be

and the total perimeter of these rectangles is

Thus we have

and so to ensure that there is at least one rectangle with it would be enough to have the perimeter bound

for a sufficiently small constant . It is here that we now see the critical nature of the exponent : for , the amount of perimeter we are permitted to have in the remaining rectangles increases as one progresses with the packing, but for the amount of perimeter one is “budgeted” for stays constant (and for the situation is even worse, in that the remaining rectangles should steadily decrease in total perimeter).

In comparison, the perimeter of the squares that one has already packed is equal to

which is comparable to for large (with the constants blowing up as approaches the critical value of ). In previous algorithms, the total perimeter of the remainder rectangles was basically comparable to the perimeter of the squares already packed, and this is the main reason why the results only worked when was sufficiently far away from . In my paper, I am able to get the perimeter of significantly smaller than the perimeter of the squares already packed, by grouping those squares into lattice-like clusters (of about squares arranged in an pattern), and sliding the squares in each cluster together to almost entirely eliminate the wasted space between each square, leaving only the space around the cluster as the main source of residual perimeter, which will be comparable to about per cluster, as compared to the total perimeter of the squares in the cluster which is comparable to . This strategy is perhaps easiest to illustrate with a picture, in which squares of slowly decreasing sidelength are packed together with relatively little wasted space:

By choosing the parameter suitably large (and taking sufficiently large depending on ), one can then prove the theorem. (In order to do some technical bookkeeping and to allow one to close an induction in the verification of the algorithm’s correctness, it is convenient to replace the perimeter by a slightly weighted variant for a small exponent , but this is a somewhat artificial device that somewhat obscures the main ideas.)

The spherical Cayley-Menger determinant and the radius of the Earth

Given three points in the plane, the distances between them have to be non-negative and obey the triangle inequalities

but are otherwise unconstrained. But if one has four points in the plane, then there is an additional constraint connecting the six distances between them, coming from the Cayley-Menger determinant:

Proposition 1 (Cayley-Menger determinant) If are four points in the plane, then the Cayley-Menger determinant

vanishes.

Proof: If we view as vectors in , then we have the usual cosine rule , and similarly for all the other distances. The matrix appearing in (1) can then be written as , where is the matrix

and is the (augmented) Gram matrix

The matrix is a rank one matrix, and so is also. The Gram matrix factorises as , where is the matrix with rows , and thus has rank at most . Therefore the matrix in (1) has rank at most , and hence has determinant zero as claimed.

For instance, if we know that and , then in order for to be coplanar, the remaining distance has to obey the equation

After some calculation the left-hand side simplifies to , so the non-negative quantity is constrained to equal either or . The former happens when form a unit right-angled triangle with right angle at and ; the latter happens when form the vertices of a unit square traversed in that order. Any other value for is not compatible with the hypothesis for lying on a plane; hence the Cayley-Menger determinant can be used as a test for planarity.

Now suppose that we have four points on a sphere of radius , with six distances now measured as lengths of arcs on the sphere. There is a spherical analogue of the Cayley-Menger determinant:

Proposition 2 (Spherical Cayley-Menger determinant) If are four points on a sphere of radius in , then the spherical Cayley-Menger determinant

vanishes.

Proof: We can assume that the sphere is centred at the origin of , and view as vectors in of magnitude . The angle subtended by from the origin is , so by the cosine rule we have

Similarly for all the other inner products. Thus the matrix in (2) can be written as , where is the Gram matrix

We can factor where is the matrix with rows . Thus has rank at most and thus the determinant vanishes as required.

Just as the Cayley-Menger determinant can be used to test for coplanarity, the spherical Cayley-Menger determinant can be used to test for lying on a sphere of radius . For instance, if we know that lie on and are all equal to , then the above proposition gives

The left-hand side evaluates to ; as lies between and , the only choices for this distance are then and . The former happens for instance when lies on the north pole , are points on the equator with longitudes differing by 90 degrees, and is also equal to the north pole; the latter occurs when is instead placed on the south pole.

The Cayley-Menger and spherical Cayley-Menger determinants look slightly different from each other, but one can transform the latter into something resembling the former by row and column operations. Indeed, the determinant (2) can be rewritten as

and by further row and column operations, this determinant vanishes if and only if the determinant

vanishes, where . In the limit (so that the curvature of the sphere tends to zero), tends to , and by Taylor expansion tends to ; similarly for the other distances. Now we see that the planar Cayley-Menger determinant emerges as the limit of (3) as , as would be expected from the intuition that a plane is essentially a sphere of infinite radius.

In principle, one can now estimate the radius of the Earth (assuming that it is either a sphere or a flat plane ) if one is given the six distances between four points on the Earth. Of course, if one wishes to do so, one should have rather far apart from each other, since otherwise it would be difficult to for instance distinguish the round Earth from a flat one. As an experiment, and just for fun, I wanted to see how accurate this would be with some real world data. I decided to take , , , be the cities of London, Los Angeles, Tokyo, and Dubai respectively. As an initial test, I used distances from this online flight calculator, measured in kilometers:

Given that the true radius of the earth was about kilometers, I chose the change of variables (so that corresponds to the round Earth model with the commonly accepted value for the Earth’s radius, and corresponds to the flat Earth), and obtained the following plot for (3):

In particular, the determinant does indeed come very close to vanishing when , which is unsurprising since, as explained on the web site, the online flight calculator uses a model in which the Earth is an ellipsoid of radii close to km. There is another radius that would also be compatible with this data at (corresponding to an Earth of radius about km), but presumably one could rule out this as a spurious coincidence by experimenting with other quadruples of cities than the ones I selected. On the other hand, these distances are highly incompatible with the flat Earth model ; one could also see this with a piece of paper and a ruler by trying to lay down four points on the paper with (an appropriately rescaled) version of the above distances (e.g., with , , etc.).

If instead one goes to the flight time calculator and uses flight travel times instead of distances, one now gets the following data (measured in hours):

Assuming that planes travel at about kilometers per hour, the true radius of the Earth should be about of flight time. If one then uses the normalisation , one obtains the following plot:

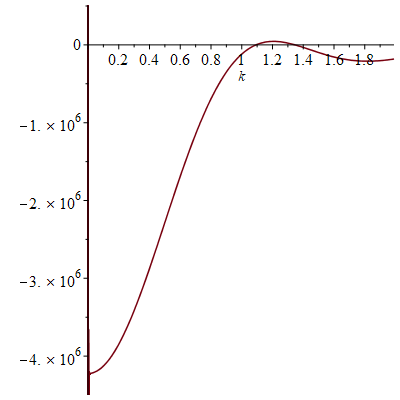
Not too surprisingly, this is basically a rescaled version of the previous plot, with vanishing near and at . (The website for the flight calculator does say it calculates short and long haul flight times slightly differently, which may be the cause of the slight discrepancies between this figure and the previous one.)

Of course, these two data sets are “cheating” since they come from a model which already presupposes what the radius of the Earth is. But one can input real world flight times between these four cities instead of the above idealised data. Here one runs into the issue that the flight time from to is not necessarily the same as that from to due to such factors as windspeed. For instance, I looked up the online flight time from Tokyo to Dubai to be 11 hours and 10 minutes, whereas the online flight time from Dubai to Tokyo was 9 hours and 50 minutes. The simplest thing to do here is take an arithmetic mean of the two times as a preliminary estimate for the flight time without windspeed factors, thus for instance the Tokyo-Dubai flight time would now be 10 hours and 30 minutes, and more generally

This data is not too far off from the online calculator data, but it does distort the graph slightly (taking as before):

Now one gets estimates for the radius of the Earth that are off by about a factor of from the truth, although the round Earth model still is twice as accurate as the flat Earth model .

Given that windspeed should additively affect flight velocity rather than flight time, and the two are inversely proportional to each other, it is more natural to take a harmonic mean rather than an arithmetic mean. This gives the slightly different values

but one still gets essentially the same plot:

So the inaccuracies are presumably coming from some other source. (Note for instance that the true flight time from Tokyo to Dubai is about greater than the calculator predicts, while the flight time from LA to Dubai is about less; these sorts of errors seem to pile up in this calculation.) Nevertheless, it does seem that flight time data is (barely) enough to establish the roundness of the Earth and obtain a somewhat ballpark estimate for its radius. (I assume that the fit would be better if one could include some Southern Hemisphere cities such as Sydney or Santiago, but I was not able to find a good quadruple of widely spaced cities on both hemispheres for which there were direct flights between all six pairs.)

Embedding the Heisenberg group into a bounded dimensional Euclidean space with optimal distortion

I’ve just uploaded to the arXiv my paper “Embedding the Heisenberg group into a bounded dimensional Euclidean space with optimal distortion“, submitted to Revista Matematica Iberoamericana. This paper concerns the extent to which one can accurately embed the metric structure of the Heisenberg group

into Euclidean space, which we can write as with the notation

Here we give the right-invariant Carnot-Carathéodory metric coming from the right-invariant vector fields

but not from the commutator vector field

This gives the geometry of a Carnot group. As observed by Semmes, it follows from the Carnot group differentiation theory of Pansu that there is no bilipschitz map from to any Euclidean space or even to , since such a map must be differentiable almost everywhere in the sense of Carnot groups, which in particular shows that the derivative map annihilate almost everywhere, which is incompatible with being bilipschitz.

On the other hand, if one snowflakes the Heisenberg group by replacing the metric with for some , then it follows from the general theory of Assouad on embedding snowflaked metrics of doubling spaces that may be embedded in a bilipschitz fashion into , or even to for some depending on .

Of course, the distortion of this bilipschitz embedding must degenerate in the limit . From the work of Austin-Naor-Tessera and Naor-Neiman it follows that may be embedded into with a distortion of , but no better. The Naor-Neiman paper also embeds into a finite-dimensional space with independent of , but at the cost of worsening the distortion to . They then posed the question of whether this worsening of the distortion is necessary.

The main result of this paper answers this question in the negative:

Theorem 1 There exists an absolute constant such that may be embedded into in a bilipschitz fashion with distortion for any .

To motivate the proof of this theorem, let us first present a bilipschitz map from the snowflaked line (with being the usual metric on ) into complex Hilbert space . The map is given explicitly as a Weierstrass type function

where for each , is the function

and are an orthonormal basis for . The subtracting of the constant is purely in order to make the sum convergent as . If are such that for some integer , one can easily check the bounds

with the lower bound

at which point one finds that

as desired.

The key here was that each function oscillated at a different spatial scale , and the functions were all orthogonal to each other (so that the upper bound involved a factor of rather than ). One can replicate this example for the Heisenberg group without much difficulty. Indeed, if we let be the discrete Heisenberg group, then the nilmanifold is a three-dimensional smooth compact manifold; thus, by the Whitney embedding theorem, it smoothly embeds into . This gives a smooth immersion which is -automorphic in the sense that for all and . If one then defines to be the function

where is the scaling map

then one can repeat the previous arguments to obtain the required bilipschitz bounds

for the function

To adapt this construction to bounded dimension, the main obstruction was the requirement that the took values in orthogonal subspaces. But if one works things out carefully, it is enough to require the weaker orthogonality requirement

for all , where is the bilinear form

One can then try to construct the for bounded dimension by an iterative argument. After some standard reductions, the problem becomes this (roughly speaking): given a smooth, slowly varying function whose derivatives obey certain quantitative upper and lower bounds, construct a smooth oscillating function , whose derivatives also obey certain quantitative upper and lower bounds, which obey the equation

We view this as an underdetermined system of differential equations for (two equations in unknowns; after some reductions, our can be taken to be the explicit value ). The trivial solution to this equation will be inadmissible for our purposes due to the lower bounds we will require on (in order to obtain the quantitative immersion property mentioned previously, as well as for a stronger “freeness” property that is needed to close the iteration). Because this construction will need to be iterated, it will be essential that the regularity control on is the same as that on ; one cannot afford to “lose derivatives” when passing from to .

This problem has some formal similarities with the isometric embedding problem (discussed for instance in this previous post), which can be viewed as the problem of solving an equation of the form , where is a Riemannian manifold and is the bilinear form

The isometric embedding problem also has the key obstacle that naive attempts to solve the equation iteratively can lead to an undesirable “loss of derivatives” that prevents one from iterating indefinitely. This obstacle was famously resolved by the Nash-Moser iteration scheme in which one alternates between perturbatively adjusting an approximate solution to improve the residual error term, and mollifying the resulting perturbation to counteract the loss of derivatives. The current equation (1) differs in some key respects from the isometric embedding equation , in particular being linear in the unknown field rather than quadratic; nevertheless the key obstacle is the same, namely that naive attempts to solve either equation lose derivatives. Our approach to solving (1) was inspired by the Nash-Moser scheme; in retrospect, I also found similarities with Uchiyama’s constructive proof of the Fefferman-Stein decomposition theorem, discussed in this previous post (and in this recent one).

To motivate this iteration, we first express using the product rule in a form that does not place derivatives directly on the unknown :

This reveals that one can construct solutions to (1) by solving the system of equations

for . Because this system is zeroth order in , this can easily be done by linear algebra (even in the presence of a forcing term ) if one imposes a “freeness” condition (analogous to the notion of a free embedding in the isometric embedding problem) that are linearly independent at each point , which (together with some other technical conditions of a similar nature) one then adds to the list of upper and lower bounds required on (with a related bound then imposed on , in order to close the iteration). However, as mentioned previously, there is a “loss of derivatives” problem with this construction: due to the presence of the differential operators in (3), a solution constructed by this method can only be expected to have two degrees less regularity than at best, which makes this construction unsuitable for iteration.

To get around this obstacle (which also prominently appears when solving (linearisations of) the isometric embedding equation ), we instead first construct a smooth, low-frequency solution to a low-frequency equation

where is a mollification of (of Littlewood-Paley type) applied at a small spatial scale for some , and then gradually relax the frequency cutoff to deform this low frequency solution to a solution of the actual equation (1).

We will construct the low-frequency solution rather explicitly, using the Whitney embedding theorem to construct an initial oscillating map into a very low dimensional space , composing it with a Veronese type embedding into a slightly larger dimensional space to obtain a required “freeness” property, and then composing further with a slowly varying isometry depending on and constructed by a quantitative topological lemma (relying ultimately on the vanishing of the first few homotopy groups of high-dimensional spheres), in order to obtain the required orthogonality (4). (This sort of “quantitative null-homotopy” was first proposed by Gromov, with some recent progress on optimal bounds by Chambers-Manin-Weinberger and by Chambers-Dotterer-Manin-Weinberger, but we will not need these more advanced results here, as one can rely on the classical qualitative vanishing for together with a compactness argument to obtain (ineffective) quantitative bounds, which suffice for this application).

To perform the deformation of into , we must solve what is essentially the linearised equation

of (1) when , (viewed as low frequency functions) are both being deformed at some rates (which should be viewed as high frequency functions). To avoid losing derivatives, the magnitude of the deformation in should not be significantly greater than the magnitude of the deformation in , when measured in the same function space norms.

As before, if one directly solves the difference equation (5) using a naive application of (2) with treated as a forcing term, one will lose at least one derivative of regularity when passing from to . However, observe that (2) (and the symmetry ) can be used to obtain the identity

and then one can solve (5) by solving the system of equations

for . The key point here is that this system is zeroth order in both and , so one can solve this system without losing any derivatives when passing from to ; compare this situation with that of the superficially similar system

that one would obtain from naively linearising (3) without exploiting the symmetry of . There is still however one residual “loss of derivatives” problem arising from the presence of a differential operator on the term, which prevents one from directly evolving this iteration scheme in time without losing regularity in . It is here that we borrow the final key idea of the Nash-Moser scheme, which is to replace by a mollified version of itself (where the projection depends on the time parameter). This creates an error term in (5), but it turns out that this error term is quite small and smooth (being a “high-high paraproduct” of and , it ends up being far more regular than either or , even with the presence of the derivatives) and can be iterated away provided that the initial frequency cutoff is large and the function has a fairly high (but finite) amount of regularity (we will eventually use the Hölder space on the Heisenberg group to measure this).

246C notes 2: Circle packings, conformal maps, and quasiconformal maps

Previous set of notes: Notes 1. Next set of notes: Notes 3.

We now leave the topic of Riemann surfaces, and turn now to the (loosely related) topic of conformal mapping (and quasiconformal mapping). Recall that a conformal map from an open subset of the complex plane to another open set is a map that is holomorphic and bijective, which (by Rouché’s theorem) also forces the derivative of to be nowhere vanishing. We then say that the two open sets are conformally equivalent. From the Cauchy-Riemann equations we see that conformal maps are orientation-preserving and angle-preserving; from the Newton approximation we see that they almost preserve small circles, indeed for small the circle will approximately map to .

In previous quarters, we proved a fundamental theorem about this concept, the Riemann mapping theorem:

Theorem 1 (Riemann mapping theorem) Let be a simply connected open subset of that is not all of . Then is conformally equivalent to the unit disk .

This theorem was proven in these 246A lecture notes, using an argument of Koebe. At a very high level, one can sketch Koebe’s proof of the Riemann mapping theorem as follows: among all the injective holomorphic maps from to that map some fixed point to , pick one that maximises the magnitude of the derivative (ignoring for this discussion the issue of proving that a maximiser exists). If avoids some point in , one can compose with various holomorphic maps and use Schwarz’s lemma and the chain rule to increase without destroying injectivity; see the previous lecture notes for details. The conformal map is unique up to Möbius automorphisms of the disk; one can fix the map by picking two distinct points in , and requiring to be zero and to be positive real.

It is a beautiful observation of Thurston that the concept of a conformal mapping has a discrete counterpart, namely the mapping of one circle packing to another. Furthermore, one can run a version of Koebe’s argument (using now a discrete version of Perron’s method) to prove the Riemann mapping theorem through circle packings. In principle, this leads to a mostly elementary approach to conformal geometry, based on extremely classical mathematics that goes all the way back to Apollonius. However, in order to prove the basic existence and uniqueness theorems of circle packing, as well as the convergence to conformal maps in the continuous limit, it seems to be necessary (or at least highly convenient) to use much more modern machinery, including the theory of quasiconformal mapping, and also the Riemann mapping theorem itself (so in particular we are not structuring these notes to provide a completely independent proof of that theorem, though this may well be possible).

To make the above discussion more precise we need some notation.

Definition 2 (Circle packing) A (finite) circle packing is a finite collection of circles in the complex numbers indexed by some finite set , whose interiors are all disjoint (but which are allowed to be tangent to each other), and whose union is connected. The nerve of a circle packing is the finite graph whose vertices are the centres of the circle packing, with two such centres connected by an edge if the circles are tangent. (In these notes all graphs are undirected, finite and simple, unless otherwise specified.)

It is clear that the nerve of a circle packing is connected and planar, since one can draw the nerve by placing each vertex (tautologically) in its location in the complex plane, and drawing each edge by the line segment between the centres of the circles it connects (this line segment will pass through the point of tangency of the two circles). Later in these notes we will also have to consider some infinite circle packings, most notably the infinite regular hexagonal circle packing.

The first basic theorem in the subject is the following converse statement:

Theorem 3 (Circle packing theorem) Every connected planar graph is the nerve of a circle packing.

Among other things, the circle packing theorem thus implies as a corollary Fáry’s theorem that every planar graph can be drawn using straight lines.

Of course, there can be multiple circle packings associated to a given connected planar graph; indeed, since reflections across a line and Möbius transformations map circles to circles (or lines), they will map circle packings to circle packings (unless one or more of the circles is sent to a line). It turns out that once one adds enough edges to the planar graph, the circle packing is otherwise rigid:

Theorem 4 (Koebe-Andreev-Thurston theorem) If a connected planar graph is maximal (i.e., no further edge can be added to it without destroying planarity), then the circle packing given by the above theorem is unique up to reflections and Möbius transformations.

Exercise 5 Let be a connected planar graph with vertices. Show that the following are equivalent:

• (i) is a maximal planar graph.
• (ii) has edges.
• (iii) Every drawing of divides the plane into faces that have three edges each, and each edge is adjacent to two distinct faces. (This includes one unbounded face.)
• (iv) At least one drawing of divides the plane into faces that have three edges each, and each edge is adjacent to two distinct faces.

(Hint: you may use without proof Euler’s formula for planar graphs, where is the number of faces including the unbounded face.)

Thurston conjectured that circle packings can be used to approximate the conformal map arising in the Riemann mapping theorem. Here is an informal statement:

Conjecture 6 (Informal Thurston conjecture) Let be a simply connected domain, with two distinct points . Let be the conformal map from to that maps to the origin and to a positive real. For any small , let be the portion of the regular hexagonal circle packing by circles of radius that are contained in , and let be an circle packing of with the same nerve (up to isomorphism) as , with all “boundary circles” tangent to , giving rise to an “approximate map” defined on the subset of consisting of the circles of , their interiors, and the interstitial regions between triples of mutually tangent circles. Normalise this map so that is zero and is a positive real. Then converges to as .

A rigorous version of this conjecture was proven by Rodin and Sullivan. Besides some elementary geometric lemmas (regarding the relative sizes of various configurations of tangent circles), the main ingredients are a rigidity result for the regular hexagonal circle packing, and the theory of quasiconformal maps. Quasiconformal maps are what seem on the surface to be a very broad generalisation of the notion of a conformal map. Informally, conformal maps take infinitesimal circles to infinitesimal circles, whereas quasiconformal maps take infinitesimal circles to infinitesimal ellipses of bounded eccentricity. In terms of Wirtinger derivatives, conformal maps obey the Cauchy-Riemann equation , while (sufficiently smooth) quasiconformal maps only obey an inequality . As such, quasiconformal maps are considerably more plentiful than conformal maps, and in particular it is possible to create piecewise smooth quasiconformal maps by gluing together various simple maps such as affine maps or Möbius transformations; such piecewise maps will naturally arise when trying to rigorously build the map alluded to in the above conjecture. On the other hand, it turns out that quasiconformal maps still have many vestiges of the rigidity properties enjoyed by conformal maps; for instance, there are quasiconformal analogues of fundamental theorems in conformal mapping such as the Schwarz reflection principle, Liouville’s theorem, or Hurwitz’s theorem. Among other things, these quasiconformal rigidity theorems allow one to create conformal maps from the limit of quasiconformal maps in many circumstances, and this will be how the Thurston conjecture will be proven. A key technical tool in establishing these sorts of rigidity theorems will be the theory of an important quasiconformal (quasi-)invariant, the conformal modulus (or, equivalently, the extremal length, which is the reciprocal of the modulus).

Homogeneous length functions on groups

The Polymath14 online collaboration has uploaded to the arXiv its paper “Homogeneous length functions on groups“, submitted to Algebra & Number Theory. The paper completely classifies homogeneous length functions on an arbitrary group , that is to say non-negative functions that obey the symmetry condition , the non-degeneracy condition , the triangle inequality , and the homogeneity condition . It turns out that these norms can only arise from pulling back the norm of a Banach space by an isometric embedding of the group. Among other things, this shows that can only support a homogeneous length function if and only if it is abelian and torsion free, thus giving a metric description of this property.

The proof is based on repeated use of the homogeneous length function axioms, combined with elementary identities of commutators, to obtain increasingly good bounds on quantities such as , until one can show that such norms have to vanish. See the previous post for a full proof. The result is robust in that it allows for some loss in the triangle inequality and homogeneity condition, allowing for some new results on “quasinorms” on groups that relate to quasihomomorphisms.

As there are now a large number of comments on the previous post on this project, this post will also serve as the new thread for any final discussion of this project as it winds down.

Metrics of linear growth – the solution

In the tradition of “Polymath projects“, the problem posed in the previous two blog posts has now been solved, thanks to the cumulative effect of many small contributions by many participants (including, but not limited to, Sean Eberhard, Tobias Fritz, Siddharta Gadgil, Tobias Hartnick, Chris Jerdonek, Apoorva Khare, Antonio Machiavelo, Pace Nielsen, Andy Putman, Will Sawin, Alexander Shamov, Lior Silberman, and David Speyer). In this post I’ll write down a streamlined resolution, eliding a number of important but ultimately removable partial steps and insights made by the above contributors en route to the solution.

Theorem 1 Let be a group. Suppose one has a “seminorm” function which obeys the triangle inequality

for all , with equality whenever . Then the seminorm factors through the abelianisation map .

Proof: By the triangle inequality, it suffices to show that for all , where is the commutator.

We first establish some basic facts. Firstly, by hypothesis we have , and hence whenever is a power of two. On the other hand, by the triangle inequality we have for all positive , and hence by the triangle inequality again we also have the matching lower bound, thus

for all . The claim is also true for (apply the preceding bound with and ). By replacing with if necessary we may now also assume without loss of generality that , thus

 

for all integers .

Next, for any , and any natural number , we have

so on taking limits as we have . Replacing by gives the matching lower bound, thus we have the conjugation invariance

 

Next, we observe that if are such that is conjugate to both and , then one has the inequality

 

Indeed, if we write for some , then for any natural number one has

where the and terms each appear times. From (2) we see that conjugation by does not affect the norm. Using this and the triangle inequality several times, we conclude that

and the claim (3) follows by sending .

The following special case of (3) will be of particular interest. Let , and for any integers , define the quantity

Observe that is conjugate to both and to , hence by (3) one has

which by (2) leads to the recursive inequality

We can write this in probabilistic notation as

where is a random vector that takes the values and with probability each. Iterating this, we conclude in particular that for any large natural number , one has

where and are iid copies of . We can write where are iid signs.  By the triangle inequality, we thus have

noting that is an even integer.  On the other hand, has mean zero and variance , hence by Cauchy-Schwarz

But by (1), the left-hand side is equal to . Dividing by and then sending , we obtain the claim.

The above theorem reduces such seminorms to abelian groups. It is easy to see from (1) that any torsion element of such groups has zero seminorm, so we can in fact restrict to torsion-free groups, which we now write using additive notation , thus for instance for . We think of as a -module. One can then extend the seminorm to the associated -vector space by the formula , and then to the associated -vector space by continuity, at which point it becomes a genuine seminorm (provided we have ensured the symmetry condition ). Conversely, any seminorm on induces a seminorm on . (These arguments also appear in this paper of Khare and Rajaratnam.)

 

Bi-invariant metrics of linear growth on the free group, II

This post is a continuation of the previous post, which has attracted a large number of comments. I’m recording here some calculations that arose from those comments (particularly those of Pace Nielsen, Lior Silberman, Tobias Fritz, and Apoorva Khare). Please feel free to either continue these calculations or to discuss other approaches to the problem, such as those mentioned in the remaining comments to the previous post.

Let be the free group on two generators , and let be a quantity obeying the triangle inequality

and the linear growth property

for all and integers ; this implies the conjugation invariance

or equivalently

We consider inequalities of the form

or

for various real numbers . For instance, since

we have (1) for . We also have the following further relations:

Proposition 1

• (i) If (1) holds for , then it holds for .
• (ii) If (1) holds for , then (2) holds for .
• (iii) If (2) holds for , then (1) holds for .
• (iv) If (1) holds for and (2) holds for , then (1) holds for .

Proof: For (i) we simply observe that

For (ii), we calculate

giving the claim.

For (iii), we calculate

giving the claim.

For (iv), we calculate

giving the claim.

Here is a typical application of the above estimates. If (1) holds for , then by part (i) it holds for , then by (ii) (2) holds for , then by (iv) (1) holds for . The map has fixed point , thus

For instance, if , then .

Bi-invariant metrics of linear growth on the free group

Here is a curious question posed to me by Apoorva Khare that I do not know the answer to. Let be the free group on two generators . Does there exist a metric on this group which is

• bi-invariant, thus for all ; and
• linear growth in the sense that for all and all natural numbers ?

By defining the “norm” of an element to be , an equivalent formulation of the problem asks if there exists a non-negative norm function that obeys the conjugation invariance

for all , the triangle inequality

for all , and the linear growth

for all and , and such that for all non-identity . Indeed, if such a norm exists then one can just take to give the desired metric.

One can normalise the norm of the generators to be at most , thus

This can then be used to upper bound the norm of other words in . For instance, from (1), (3) one has

A bit less trivially, from (3), (2), (1) one can bound commutators as

In a similar spirit one has

What is not clear to me is if one can keep arguing like this to continually improve the upper bounds on the norm of a given non-trivial group element to the point where this norm must in fact vanish, which would demonstrate that no metric with the above properties on would exist (and in fact would impose strong constraints on similar metrics existing on other groups as well). It is also tempting to use some ideas from geometric group theory (e.g. asymptotic cones) to try to understand these metrics further, though I wasn’t able to get very far with this approach. Anyway, this feels like a problem that might be somewhat receptive to a more crowdsourced attack, so I am posing it here in case any readers wish to try to make progress on it.

On the universality of the incompressible Euler equation on compact manifolds

I’ve just uploaded to the arXiv my paper “On the universality of the incompressible Euler equation on compact manifolds“, submitted to Discrete and Continuous Dynamical Systems. This is a variant of my recent paper on the universality of potential well dynamics, but instead of trying to embed dynamical systems into a potential well , here we try to embed dynamical systems into the incompressible Euler equations

on a Riemannian manifold . (One is particularly interested in the case of flat manifolds , particularly or , but for the main result of this paper it is essential that one is permitted to consider curved manifolds.) This system, first studied by Ebin and Marsden, is the natural generalisation of the usual incompressible Euler equations to curved space; it can be viewed as the formal geodesic flow equation on the infinite-dimensional manifold of volume-preserving diffeomorphisms on (see this previous post for a discussion of this in the flat space case).

The Euler equations can be viewed as a nonlinear equation in which the nonlinearity is a quadratic function of the velocity field . It is thus natural to compare the Euler equations with quadratic ODE of the form

where is the unknown solution, and is a bilinear map, which we may assume without loss of generality to be symmetric. One can ask whether such an ODE may be linearly embedded into the Euler equations on some Riemannian manifold , which means that there is an injective linear map from to smooth vector fields on , as well as a bilinear map to smooth scalar fields on , such that the map takes solutions to (2) to solutions to (1), or equivalently that

for all .

For simplicity let us restrict to be compact. There is an obvious necessary condition for this embeddability to occur, which comes from energy conservation law for the Euler equations; unpacking everything, this implies that the bilinear form in (2) has to obey a cancellation condition

for some positive definite inner product on . The main result of the paper is the converse to this statement: if is a symmetric bilinear form obeying a cancellation condition (3), then it is possible to embed the equations (2) into the Euler equations (1) on some Riemannian manifold ; the catch is that this manifold will depend on the form and on the dimension (in fact in the construction I have, is given explicitly as , with a funny metric on it that depends on ).

As a consequence, any finite dimensional portion of the usual “dyadic shell models” used as simplified toy models of the Euler equation, can actually be embedded into a genuine Euler equation, albeit on a high-dimensional and curved manifold. This includes portions of the self-similar “machine” I used in a previous paper to establish finite time blowup for an averaged version of the Navier-Stokes (or Euler) equations. Unfortunately, the result in this paper does not apply to infinite-dimensional ODE, so I cannot yet establish finite time blowup for the Euler equations on a (well-chosen) manifold. It does not seem so far beyond the realm of possibility, though, that this could be done in the relatively near future. In particular, the result here suggests that one could construct something resembling a universal Turing machine within an Euler flow on a manifold, which was one ingredient I would need to engineer such a finite time blowup.

The proof of the main theorem proceeds by an “elimination of variables” strategy that was used in some of my previous papers in this area, though in this particular case the Nash embedding theorem (or variants thereof) are not required. The first step is to lessen the dependence on the metric by partially reformulating the Euler equations (1) in terms of the covelocity (which is a -form) instead of the velocity . Using the freedom to modify the dimension of the underlying manifold , one can also decouple the metric from the volume form that is used to obtain the divergence-free condition. At this point the metric can be eliminated, with a certain positive definiteness condition between the velocity and covelocity taking its place. After a substantial amount of trial and error (motivated by some “two-and-a-half-dimensional” reductions of the three-dimensional Euler equations, and also by playing around with a number of variants of the classic “separation of variables” strategy), I eventually found an ansatz for the velocity and covelocity that automatically solved most of the components of the Euler equations (as well as most of the positive definiteness requirements), as long as one could find a number of scalar fields that obeyed a certain nonlinear system of transport equations, and also obeyed a positive definiteness condition. Here I was stuck for a bit because the system I ended up with was overdetermined – more equations than unknowns. After trying a number of special cases I eventually found a solution to the transport system on the sphere, except that the scalar functions sometimes degenerated and so the positive definiteness property I wanted was only obeyed with positive semi-definiteness. I tried for some time to perturb this example into a strictly positive definite solution before eventually working out that this was not possible. Finally I had the brainwave to lift the solution from the sphere to an even more symmetric space, and this quickly led to the final solution of the problem, using the special orthogonal group rather than the sphere as the underlying domain. The solution ended up being rather simple in form, but it is still somewhat miraculous to me that it exists at all; in retrospect, given the overdetermined nature of the problem, relying on a large amount of symmetry to cut down the number of equations was basically the only hope.