Monthly Archive

You are currently browsing the monthly archive for June 2020.

Homogenization of iterated singular integrals with applications to random quasiconformal maps

22 June, 2020 in math.CA, math.CV, paper | Tags: , , , , , | by | 10 comments

Kari Astala, Steffen Rohde, Eero Saksman and I have (finally!) uploaded to the arXiv our preprint “Homogenization of iterated singular integrals with applications to random quasiconformal maps“. This project started (and was largely completed) over a decade ago, but for various reasons it was not finalised until very recently. The motivation for this project was to study the behaviour of “random” quasiconformal maps. Recall that a (smooth) quasiconformal map is a homeomorphism {f: {\bf C} \rightarrow {\bf C}} that obeys the Beltrami equation

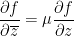
\displaystyle \frac{\partial f}{\partial \overline{z}} = \mu \frac{\partial f}{\partial z}

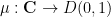
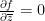
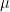
for some Beltrami coefficient {\mu: {\bf C} \rightarrow D(0,1)}; this can be viewed as a deformation of the Cauchy-Riemann equation {\frac{\partial f}{\partial \overline{z}} = 0}. Assuming that {f(z)} is asymptotic to {z} at infinity, one can (formally, at least) solve for {f} in terms of {\mu} using the Beurling transform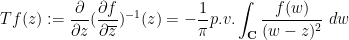

\displaystyle Tf(z) := \frac{\partial}{\partial z}(\frac{\partial f}{\partial \overline{z}})^{-1}(z) = -\frac{1}{\pi} p.v. \int_{\bf C} \frac{f(w)}{(w-z)^2}\ dw

by the Neumann series

\displaystyle \frac{\partial f}{\partial \overline{z}} = \mu + \mu T \mu + \mu T \mu T \mu + \dots.

We looked at the question of the asymptotic behaviour of {f} if {\mu = \mu_\delta} is a random field that oscillates at some fine spatial scale {\delta>0}. A simple model to keep in mind is

\displaystyle \mu_\delta(z) = \varphi(z) \sum_{n \in {\bf Z}^2} \epsilon_n 1_{n\delta + [0,\delta]^2}(z) \ \ \ \ \ (1)

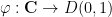
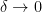
 where {\epsilon_n = \pm 1} are independent random signs and {\varphi: {\bf C} \rightarrow D(0,1)} is a bump function. For models such as these, we show that a homogenisation occurs in the limit {\delta \rightarrow 0}; each multilinear expression

\displaystyle \mu_\delta T \mu_\delta \dots T \mu_\delta \ \ \ \ \ (2)

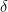
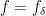
 converges weakly in probability (and almost surely, if we restrict {\delta} to a lacunary sequence) to a deterministic limit, and the associated quasiconformal map {f = f_\delta} similarly converges weakly in probability (or almost surely). (Results of this latter type were also recently obtained by Ivrii and Markovic by a more geometric method which is simpler, but is applied to a narrower class of Beltrami coefficients.) In the specific case (1), the limiting quasiconformal map is just the identity map {f(z)=z}, but if for instance replaces the {\epsilon_n} by non-symmetric random variables then one can have significantly more complicated limits. 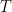The convergence theorem for multilinear expressions such as is not specific to the Beurling transform {T}; any other translation and dilation invariant singular integral can be used here.

The random expression (2) is somewhat reminiscent of a moment of a random matrix, and one can start computing it analogously. For instance, if one has a decomposition 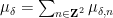{\mu_\delta = \sum_{n \in {\bf Z}^2} \mu_{\delta,n}} such as (1), then (2) expands out as a sum

\displaystyle \sum_{n_1,\dots,n_k \in {\bf Z}^2} \mu_{\delta,n_1} T \mu_{\delta,n_2} \dots T \mu_{\delta,n_k}

The random fluctuations of this sum can be treated by a routine second moment estimate, and the main task is to show that the expected value

\displaystyle \sum_{n_1,\dots,n_k \in {\bf Z}^2} \mathop{\bf E}(\mu_{\delta,n_1} T \mu_{\delta,n_2} \dots T \mu_{\delta,n_k}) \ \ \ \ \ (3)

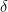
 becomes asymptotically independent of {\delta}.

If all the 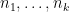{n_1,\dots,n_k} were distinct then one could use independence to factor the expectation to get

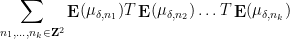
\displaystyle \sum_{n_1,\dots,n_k \in {\bf Z}^2} \mathop{\bf E}(\mu_{\delta,n_1}) T \mathop{\bf E}(\mu_{\delta,n_2}) \dots T \mathop{\bf E}(\mu_{\delta,n_k})

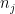
which is a relatively straightforward expression to calculate (particularly in the model (1), where all the expectations here in fact vanish). The main difficulty is that there are a number of configurations in (3) in which various of the {n_j} collide with each other, preventing one from easily factoring the expression. A typical problematic contribution for instance would be a sum of the form

\displaystyle \sum_{n_1,n_2 \in {\bf Z}^2: n_1 \neq n_2} \mathop{\bf E}(\mu_{\delta,n_1} T \mu_{\delta,n_2} T \mu_{\delta,n_1} T \mu_{\delta,n_2}). \ \ \ \ \ (4)

 This is an example of what we call a non-split sum. This can be compared with the split sum

\displaystyle \sum_{n_1,n_2 \in {\bf Z}^2: n_1 \neq n_2} \mathop{\bf E}(\mu_{\delta,n_1} T \mu_{\delta,n_1} T \mu_{\delta,n_2} T \mu_{\delta,n_2}). \ \ \ \ \ (5)

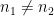
 If we ignore the constraint {n_1 \neq n_2} in the latter sum, then it splits into

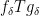
\displaystyle f_\delta T g_\delta

where

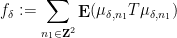
\displaystyle f_\delta := \sum_{n_1 \in {\bf Z}^2} \mathop{\bf E}(\mu_{\delta,n_1} T \mu_{\delta,n_1})

and

\displaystyle g_\delta := \sum_{n_2 \in {\bf Z}^2} \mathop{\bf E}(\mu_{\delta,n_2} T \mu_{\delta,n_2})

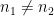
and one can hope to treat this sum by an induction hypothesis. (To actually deal with constraints such as {n_1 \neq n_2} requires an inclusion-exclusion argument that creates some notational headaches but is ultimately manageable.) As the name suggests, the non-split configurations such as (4) cannot be factored in this fashion, and are the most difficult to handle. A direct computation using the triangle inequality (and a certain amount of combinatorics and induction) reveals that these sums are somewhat localised, in that dyadic portions such as

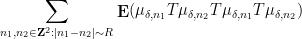
\displaystyle \sum_{n_1,n_2 \in {\bf Z}^2: |n_1 - n_2| \sim R} \mathop{\bf E}(\mu_{\delta,n_1} T \mu_{\delta,n_2} T \mu_{\delta,n_1} T \mu_{\delta,n_2})

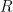
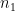
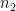
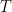
exhibit power decay in {R} (when measured in suitable function space norms), basically because of the large number of times one has to transition back and forth between {n_1} and {n_2}. Thus, morally at least, the dominant contribution to a non-split sum such as (4) comes from the local portion when {n_2=n_1+O(1)}. From the translation and dilation invariance of {T} this type of expression then simplifies to something like

\displaystyle \varphi(z)^4 \sum_{n \in {\bf Z}^2} \eta( \frac{n-z}{\delta} )

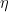
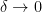
(plus negligible errors) for some reasonably decaying function {\eta}, and this can be shown to converge to a weak limit as {\delta \rightarrow 0}.

In principle all of these limits are computable, but the combinatorics is remarkably complicated, and while there is certainly some algebraic structure to the calculations, it does not seem to be easily describable in terms of an existing framework (e.g., that of free probability).

Archives