Yoneda’s lemma as an identification of form and function: the case study of polynomials

As someone who had a relatively light graduate education in algebra, the import of Yoneda’s lemma in category theory has always eluded me somewhat; the statement and proof are simple enough, but definitely have the “abstract nonsense” flavor that one often ascribes to this part of mathematics, and I struggled to connect it to the more grounded forms of intuition, such as those based on concrete examples, that I was more comfortable with. There is a popular MathOverflow post devoted to this question, with many answers that were helpful to me, but I still felt vaguely dissatisfied. However, recently when pondering the very concrete concept of a polynomial, I managed to accidentally stumble upon a special case of Yoneda’s lemma in action, which clarified this lemma conceptually for me. In the end it was a very simple observation (and would be extremely pedestrian to anyone who works in an algebraic field of mathematics), but as I found this helpful to a non-algebraist such as myself, and I thought I would share it here in case others similarly find it helpful.

In algebra we see a distinction between a polynomial form (also known as a formal polynomial), and a polynomial function, although this distinction is often elided in more concrete applications. A polynomial form in, say, one variable with integer coefficients, is a formal expression of the form

where are coefficients in the integers, and is an indeterminate: a symbol that is often intended to be interpreted as an integer, real number, complex number, or element of some more general ring , but is for now a purely formal object. The collection of such polynomial forms is denoted , and is a commutative ring.

A polynomial form can be interpreted in any ring (even non-commutative ones) to create a polynomial function , defined by the formula

for any . This definition (2) looks so similar to the definition (1) that we usually abuse notation and conflate with . This conflation is supported by the identity theorem for polynomials, that asserts that if two polynomial forms agree at an infinite number of (say) complex numbers, thus for infinitely many , then they agree as polynomial forms (i.e., their coefficients match). But this conflation is sometimes dangerous, particularly when working in finite characteristic. For instance:

• (i) The linear forms and are distinct as polynomial forms, but agree when interpreted in the ring , since for all .
• (ii) Similarly, if is a prime, then the degree one form and the degree form are distinct as polynomial forms (and in particular have distinct degrees), but agree when interpreted in the ring , thanks to Fermat’s little theorem.
• (iii) The polynomial form has no roots when interpreted in the reals , but has roots when interpreted in the complex numbers . Similarly, the linear form has no roots when interpreted in the integers , but has roots when interpreted in the rationals .

The above examples show that if one only interprets polynomial forms in a specific ring , then some information about the polynomial could be lost (and some features of the polynomial, such as roots, may be “invisible” to that interpretation). But this turns out not to be the case if one considers interpretations in all rings simultaneously, as we shall now discuss.

If are two different rings, then the polynomial functions and arising from interpreting a polynomial form in these two rings are, strictly speaking, different functions. However, they are often closely related to each other. For instance, if is a subring of , then agrees with the restriction of to . More generally, if there is a ring homomorphism from to , then and are intertwined by the relation

which basically asserts that ring homomorphism respect polynomial operations. Note that the previous observation corresponded to the case when was an inclusion homomorphism. Another example comes from the complex conjugation automorphism on the complex numbers, in which case (3) asserts the identity

for any polynomial function on the complex numbers, and any complex number .

What was surprising to me (as someone who had not internalized the Yoneda lemma) was that the converse statement was true: if one had a function associated to every ring that obeyed the intertwining relation

for every ring homomorphism , then there was a unique polynomial form such that for all rings . This seemed surprising to me because the functions were a priori arbitrary functions, and as an analyst I would not expect them to have polynomial structure. But the fact that (4) holds for all rings and all homomorphisms is in fact rather powerful. As an analyst, I am tempted to proceed by first working with the ring of complex numbers and taking advantage of the aforementioned identity theorem, but this turns out to be tricky because does not “talk” to all the other rings enough, in the sense that there are not always as many ring homomorphisms from to as one would like. But there is in fact a more elementary argument that takes advantage of a particularly relevant (and “talkative”) ring to the theory of polynomials, namely the ring of polynomials themselves. Given any other ring , and any element of that ring, there is a unique ring homomorphism from to that maps to , namely the evaluation map

that sends a polynomial form to its evaluation at . Applying (4) to this ring homomorphism, and specializing to the element of , we conclude that

for any ring and any . If we then define to be the formal polynomial

then this identity can be rewritten as

and so we have indeed shown that the family arises from a polynomial form . Conversely, from the identity

valid for any polynomial form , we see that two polynomial forms can only generate the same polynomial functions for all rings if they are identical as polynomial forms. So the polynomial form associated to the family is unique.

We have thus created an identification of form and function: polynomial forms are in one-to-one correspondence with families of functions obeying the intertwining relation (4). But this identification can be interpreted as a special case of the Yoneda lemma, as follows. There are two categories in play here: the category of rings (where the morphisms are ring homomorphisms), and the category of sets (where the morphisms are arbitrary functions). There is an obvious forgetful functor between these two categories that takes a ring and removes all of the algebraic structure, leaving behind just the underlying set. A collection of functions (i.e., -morphisms) for each in that obeys the intertwining relation (4) is precisely the same thing as a natural transformation from the forgetful functor to itself. So we have identified formal polynomials in as a set with natural endomorphisms of the forgetful functor:

Informally: polynomial forms are precisely those operations on rings that are respected by ring homomorphisms.

What does this have to do with Yoneda’s lemma? Well, remember that every element of a ring came with an evaluation homomorphism . Conversely, every homomorphism from to will be of the form for a unique – indeed, will just be the image of under this homomorphism. So the evaluation homomorphism provides a one-to-one correspondence between elements of , and ring homomorphisms in . This correspondence is at the level of sets, so this gives the identification

Thus our identification can be written as

which is now clearly a special case of the Yoneda lemma

that applies to any functor from a (locally small) category and any object in . And indeed if one inspects the standard proof of this lemma, it is essentially the same argument as the argument we used above to establish the identification (5). More generally, it seems to me that the Yoneda lemma is often used to identify “formal” objects with their “functional” interpretations, as long as one simultaneously considers interpretations across an entire category (such as the category of rings), as opposed to just a single interpretation in a single object of the category in which there may be some loss of information due to the peculiarities of that specific object. Grothendieck’s “functor of points” interpretation of a scheme, discussed in this previous blog post, is one typical example of this.

Sums of GUE matrices and concentration of hives from correlation decay of eigengaps

Hariharan Narayanan, Scott Sheffield, and I have just uploaded to the arXiv our paper “Sums of GUE matrices and concentration of hives from correlation decay of eigengaps“. This is a personally satisfying paper for me, as it connects the work I did as a graduate student (with Allen Knutson and Chris Woodward) on sums of Hermitian matrices, with more recent work I did (with Van Vu) on random matrix theory, as well as several other results by other authors scattered across various mathematical subfields.

Suppose are two Hermitian matrices with eigenvalues and respectively (arranged in non-increasing order. What can one say about the eigenvalues of the sum ? There are now many ways to answer this question precisely; one of them, introduced by Allen and myself many years ago, is that there exists a certain triangular array of numbers called a “hive” that has as its boundary values. On the other hand, by the pioneering work of Voiculescu in free probability, we know in the large limit that if are asymptotically drawn from some limiting distribution, and and are drawn independently at random (using the unitarily invariant Haar measure) amongst all Hermitian matrices with the indicated eigenvalues, then (under mild hypotheses on the distribution, and under suitable normalization), will almost surely have a limiting distribution that is the free convolution of the two original distributions.

One of my favourite open problems is to come up with a theory of “free hives” that allows one to explain the latter fact from the former. This is still unresolved, but we are now beginning to make a bit of progress towards this goal. We know (for instance from the calculations of Coquereaux and Zuber) that if are drawn independently at random with eigenvalues , then the eigenvalues of are distributed according to the boundary values of an “augmented hive” with two boundaries , drawn uniformly at random from the polytope of all such augmented hives. (This augmented hive is basically a regular hive with another type of pattern, namely a Gelfand-Tsetlin pattern, glued to one side of it.) So, if one could show some sort of concentration of measure for the entries of this augmented hive, and calculate what these entries concentrated to, one should presumably be able to recover Voiculescu’s result after some calculation.

In this paper, we are able to accomplish the first half of this goal, assuming that the spectra are not deterministic, but rather drawn from the spectra of rescaled GUE matrices (thus are independent rescaled copies of the GUE ensemble). We have chosen to normalize matters so that the eigenvalues have size , so that the entries of the augmented hive have entries . Our result is then that the entries of the augmented hive in fact have a standard deviation of , thus exhibiting a little bit of concentration. (Actually, from the Brunn-Minkowski inequality, the distribution of these entries is log concave, so once once controls the standard deviation one also gets a bit of exponential decay beyond the standard deviation; Narayanan and Sheffield had also recently established the existence of a rate function for this sort of model.) Presumably one should get much better concentration, and one should be able to handle other models than the GUE ensemble, but this is the first advance that we were able to achieve.

Augmented hives seem tricky to work with directly, but by adapting the octahedron recurrence introduced for this problem by Knutson, Woodward, and myself some time ago (which is related to the associativity of addition for Hermitian matrices), one can construct a piecewise linear volume-preserving map between the cone of augmented hives, and the product of two Gelfand-Tsetlin cones. The problem then reduces to establishing concentration of measure for certain piecewise linear maps on products of Gelfand-Tsetlin cones (endowed with a certain GUE-type measure). This is a promising formulation because Gelfand-Tsetlin cones are by now quite well understood.

On the other hand, the piecewise linear map, initially defined by iterating the octahedron relation , looks somewhat daunting. Fortunately, there is an explicit formulation of this map due to Speyer, as the supremum of certain linear maps associated to perfect matchings of a certain “excavation graph”. For us it was convenient to work with the dual of this excavation graph, and associate these linear maps to certain “lozenge tilings” of a hexagon.

It would be more convenient to study the concentration of each linear map separately, rather than their supremum. By the Cheeger inequality, it turns out that one can relate the latter to the former provided that one has good control on the Cheeger constant of the underlying measure on the Gelfand-Tsetlin cones. Fortunately, the measure is log-concave, so one can use the very recent work of Klartag on the KLS conjecture to eliminate the supremum (up to a logarithmic loss which is only moderately annoying to deal with).

It remains to obtain concentration on the linear map associated to a given lozenge tiling. After stripping away some contributions coming from lozenges near the edge (using some eigenvalue rigidity results of Van Vu and myself), one is left with some bulk contributions which ultimately involve eigenvalue interlacing gaps such as

where is the eigenvalue of the top left minor of , and is in the bulk region for some fixed . To get the desired result, one needs some non-trivial correlation decay in for these statistics. If one was working with eigenvalue gaps rather than interlacing results, then such correlation decay was conveniently obtained for us by recent work of Cippoloni, Erdös, and Schröder. So the last remaining challenge is to understand the relation between eigenvalue gaps and interlacing gaps.

For this we turned to the work of Metcalfe, who uncovered a determinantal process structure to this problem, with a kernel associated to Lagrange interpolation polynomials. It is possible to satisfactorily estimate various integrals of these kernels using the residue theorem and eigenvalue rigidity estimates, thus completing the required analysis.

Using the Smith normal form to manipulate lattice subgroups and closed torus subgroups

Let denote the space of matrices with integer entries, and let be the group of invertible matrices with integer entries. The Smith normal form takes an arbitrary matrix and factorises it as , where , , and is a rectangular diagonal matrix, by which we mean that the principal minor is diagonal, with all other entries zero. Furthermore the diagonal entries of are for some (which is also the rank of ) with the numbers (known as the invariant factors) principal divisors with . The invariant factors are uniquely determined; but there can be some freedom to modify the invertible matrices . The Smith normal form can be computed easily; for instance, in SAGE, it can be computed calling the function from the matrix class. The Smith normal form is also available for other principal ideal domains than the integers, but we will only be focused on the integer case here. For the purposes of this post, we will view the Smith normal form as a primitive operation on matrices that can be invoked as a “black box”.

In this post I would like to record how to use the Smith normal form to computationally manipulate two closely related classes of objects:

• Subgroups of a standard lattice (or lattice subgroups for short);
• Closed subgroups of a standard torus (or closed torus subgroups for short).

(This arose for me due to the need to actually perform (with a collaborator) some numerical calculations with a number of lattice subgroups and closed torus subgroups.) It’s possible that all of these operations are already encoded in some existing object classes in a computational algebra package; I would be interested to know of such packages and classes for lattice subgroups or closed torus subgroups in the comments.

The above two classes of objects are isomorphic to each other by Pontryagin duality: if is a lattice subgroup, then the orthogonal complement

is a closed torus subgroup (with the usual Fourier pairing); conversely, if is a closed torus subgroup, then

is a lattice subgroup. These two operations invert each other: and .

Example 1 The orthogonal complement of the lattice subgroup

is the closed torus subgroup

and conversely.

Let us focus first on lattice subgroups . As all such subgroups are finitely generated abelian groups, one way to describe a lattice subgroup is to specify a set of generators of . Equivalently, we have

where is the matrix whose columns are . Applying the Smith normal form , we conclude that

so in particular is isomorphic (with respect to the automorphism group of ) to . In particular, we see that is a free abelian group of rank , where is the rank of (or ). This representation also allows one to trim the representation down to , where is the matrix formed from the left columns of ; the columns of then give a basis for . Let us call this a trimmed representation of .

Example 2 Let be the lattice subgroup generated by , , , thus with . A Smith normal form for is given by

so is a rank two lattice with a basis of and (and the invariant factors are and ). The trimmed representation is

There are other Smith normal forms for , giving slightly different representations here, but the rank and invariant factors will always be the same.

By the above discussion we can represent a lattice subgroup by a matrix for some ; this representation is not unique, but we will address this issue shortly. For now, we focus on the question of how to use such data representations of subgroups to perform basic operations on lattice subgroups. There are some operations that are very easy to perform using this data representation:

• (Applying a linear transformation) if , so that is also a linear transformation from to , then maps lattice subgroups to lattice subgroups, and clearly maps the lattice subgroup to for any .
• (Sum) Given two lattice subgroups for some , , the sum is equal to the lattice subgroup , where is the matrix formed by concatenating the columns of with the columns of .
• (Direct sum) Given two lattice subgroups , , the direct sum is equal to the lattice subgroup , where is the block matrix formed by taking the direct sum of and .

One can also use Smith normal form to detect when one lattice subgroup is a subgroup of another lattice subgroup . Using Smith normal form factorization , with invariant factors , the relation is equivalent after some manipulation to

The group is generated by the columns of , so this gives a test to determine whether : the row of must be divisible by for , and all other rows must vanish.

Example 3 To test whether the lattice subgroup generated by and is contained in the lattice subgroup from Example 2, we write as with , and observe that

The first row is of course divisible by , and the last row vanishes as required, but the second row is not divisible by , so is not contained in (but is); also a similar computation verifies that is conversely contained in .

One can now test whether by testing whether and simultaneously hold (there may be more efficient ways to do this, but this is already computationally manageable in many applications). This in principle addresses the issue of non-uniqueness of representation of a subgroup in the form .

Next, we consider the question of representing the intersection of two subgroups in the form for some and . We can write

where is the matrix formed by concatenating and , and similarly for (here we use the change of variable ). We apply the Smith normal form to to write

where , , with of rank . We can then write

(making the change of variables ). Thus we can write where consists of the right columns of .

Example 4 With the lattice from Example 2, we shall compute the intersection of with the subgroup , which one can also write as with . We obtain a Smith normal form

so . We have

and so we can write where

One can trim this representation if desired, for instance by deleting the first column of (and replacing with ). Thus the intersection of with is the rank one subgroup generated by .

A similar calculation allows one to represent the pullback of a subgroup via a linear transformation , since

where is the concatenation of the identity matrix and the zero matrix. Applying the Smith normal form to write with of rank , the same argument as before allows us to write where consists of the right columns of .

Among other things, this allows one to describe lattices given by systems of linear equations and congruences in the format. Indeed, the set of lattice vectors that solve the system of congruences

for , some natural numbers , and some lattice vectors , together with an additional system of equations

for and some lattice vectors , can be written as where is the matrix with rows , and is the diagonal matrix with diagonal entries . Conversely, any subgroup can be described in this form by first using the trimmed representation , at which point membership of a lattice vector in is seen to be equivalent to the congruences

for (where is the rank, are the invariant factors, and is the standard basis of ) together with the equations

for . Thus one can obtain a representation in the form (1), (2) with , and to be the rows of in order.

Example 5 With the lattice subgroup from Example 2, we have , and so consists of those triples which obey the (redundant) congruence

the congruence

and the identity

Conversely, one can use the above procedure to convert the above system of congruences and identities back into a form (though depending on which Smith normal form one chooses, the end result may be a different representation of the same lattice group ).

Now we apply Pontryagin duality. We claim the identity

for any (where induces a homomorphism from to in the obvious fashion). This can be verified by direct computation when is a (rectangular) diagonal matrix, and the general case then easily follows from a Smith normal form computation (one can presumably also derive it from the category-theoretic properties of Pontryagin duality, although I will not do so here). So closed torus subgroups that are defined by a system of linear equations (over , with integer coefficients) are represented in the form of an orthogonal complement of a lattice subgroup. Using the trimmed form , we see that

giving an explicit representation “in coordinates” of such a closed torus subgroup. In particular we can read off the isomorphism class of a closed torus subgroup as the product of a finite number of cyclic groups and a torus:

Example 6 The orthogonal complement of the lattice subgroup from Example 2 is the closed torus subgroup

using the trimmed representation of , one can simplify this a little to

and one can also write this as the image of the group under the torus isomorphism

In other words, one can write

so that is isomorphic to .

We can now dualize all of the previous computable operations on subgroups of to produce computable operations on closed subgroups of . For instance:

• To form the intersection or sum of two closed torus subgroups , use the identities

  

  and

  

  and then calculate the sum or intersection of the lattice subgroups by the previous methods. Similarly, the operation of direct sum of two closed torus subgroups dualises to the operation of direct sum of two lattice subgroups.
• To determine whether one closed torus subgroup is contained in (or equal to) another closed torus subgroup , simply use the preceding methods to check whether the lattice subgroup is contained in (or equal to) the lattice subgroup .
• To compute the pull back of a closed torus subgroup via a linear transformation , use the identity

  

  Similarly, to compute the image of a closed torus subgroup , use the identity

  

Example 7 Suppose one wants to compute the sum of the closed torus subgroup from Example 6 with the closed torus subgroup . This latter group is the orthogonal complement of the lattice subgroup considered in Example 4. Thus we have where is the matrix from Example 6; discarding the zero column, we thus have

Satz vom Nullprodukt

As I have mentioned in some recent posts, I am interested in exploring unconventional modalities for presenting mathematics, for instance using media with high production value. One such recent example of this I saw was a presentation of the fundamental zero product property (or domain property) of the real numbers – namely, that implies or for real numbers – expressed through the medium of German-language rap:

EDIT: and here is a lesson on fractions, expressed through the medium of a burger chain advertisement:

I’d be interested to know what further examples of this type are out there.

SECOND EDIT: The following two examples from Wired magazine are slightly more conventional in nature, but still worth mentioning, I think. Firstly, my colleague at UCLA, Amit Sahai, presents the concept of zero knowledge proofs at various levels of technicality:

Secondly, Moon Duchin answers math questions of all sorts from Twitter:

Venn and Euler type diagrams for vector spaces and abelian groups

A popular way to visualise relationships between some finite number of sets is via Venn diagrams, or more generally Euler diagrams. In these diagrams, a set is depicted as a two-dimensional shape such as a disk or a rectangle, and the various Boolean relationships between these sets (e.g., that one set is contained in another, or that the intersection of two of the sets is equal to a third) is represented by the Boolean algebra of these shapes; Venn diagrams correspond to the case where the sets are in “general position” in the sense that all non-trivial Boolean combinations of the sets are non-empty. For instance to depict the general situation of two sets together with their intersection and one might use a Venn diagram such as

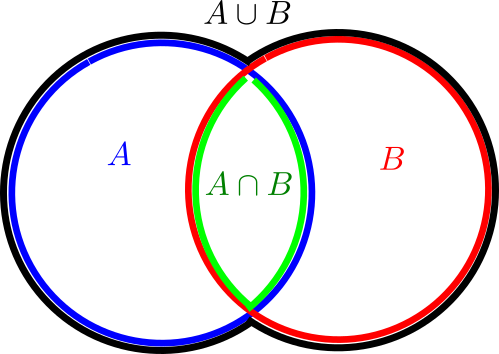
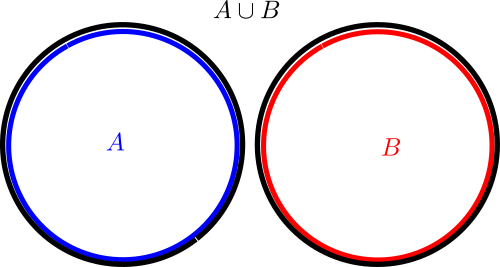
(where we have given each region depicted a different color, and moved the edges of each region a little away from each other in order to make them all visible separately), but if one wanted to instead depict a situation in which the intersection was empty, one could use an Euler diagram such as

One can use the area of various regions in a Venn or Euler diagram as a heuristic proxy for the cardinality (or measure ) of the set corresponding to such a region. For instance, the above Venn diagram can be used to intuitively justify the inclusion-exclusion formula

for finite sets , while the above Euler diagram similarly justifies the special case

for finite disjoint sets .

While Venn and Euler diagrams are traditionally two-dimensional in nature, there is nothing preventing one from using one-dimensional diagrams such as

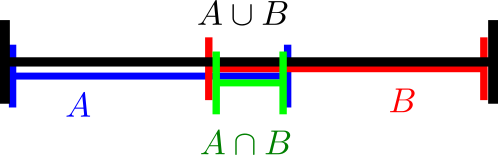
or even three-dimensional diagrams such as this one from Wikipedia:

Of course, in such cases one would use length or volume as a heuristic proxy for cardinality or measure, rather than area.

With the addition of arrows, Venn and Euler diagrams can also accommodate (to some extent) functions between sets. Here for instance is a depiction of a function , the image of that function, and the image of some subset of :

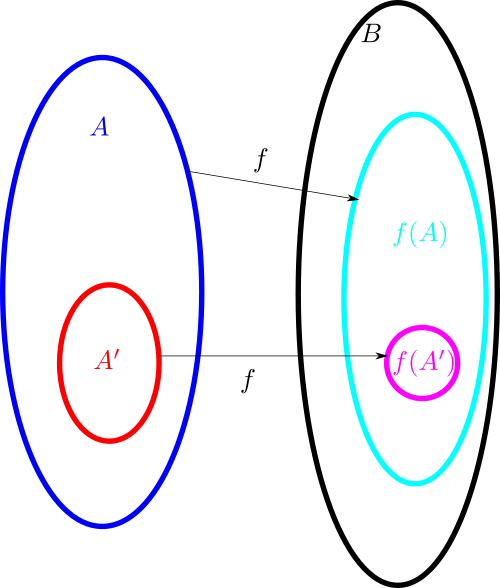
Here one can illustrate surjectivity of by having fill out all of ; one can similarly illustrate injectivity of by giving exactly the same shape (or at least the same area) as . So here for instance might be how one would illustrate an injective function :

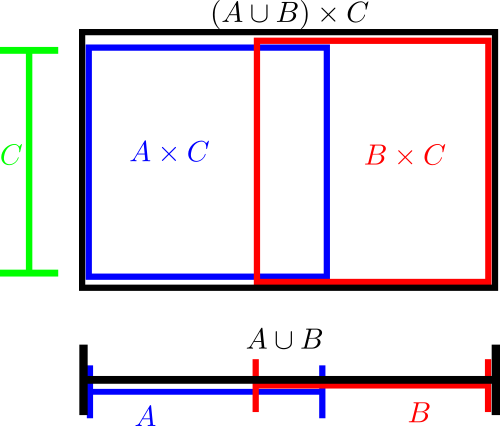
Cartesian product operations can be incorporated into these diagrams by appropriate combinations of one-dimensional and two-dimensional diagrams. Here for instance is a diagram that illustrates the identity :

In this blog post I would like to propose a similar family of diagrams to illustrate relationships between vector spaces (over a fixed base field , such as the reals) or abelian groups, rather than sets. The categories of (-)vector spaces and abelian groups are quite similar in many ways; the former consists of modules over a base field , while the latter consists of modules over the integers ; also, both categories are basic examples of abelian categories. The notion of a dimension in a vector space is analogous in many ways to that of cardinality of a set; see this previous post for an instance of this analogy (in the context of Shannon entropy). (UPDATE: I have learned that an essentially identical notation has also been proposed in an unpublished manuscript of Ravi Vakil.)

The inclusion-exclusion principle for commuting projections

The (classical) Möbius function is the unique function that obeys the classical Möbius inversion formula:

Proposition 1 (Classical Möbius inversion) Let be functions from the natural numbers to an additive group . Then the following two claims are equivalent:

• (i) for all .
• (ii) for all .

There is a generalisation of this formula to (finite) posets, due to Hall, in which one sums over chains in the poset:

Proposition 2 (Poset Möbius inversion) Let be a finite poset, and let be functions from that poset to an additive group . Then the following two claims are equivalent:

• (i) for all , where is understood to range in .
• (ii) for all , where in the inner sum are understood to range in with the indicated ordering.

(Note from the finite nature of that the inner sum in (ii) is vacuous for all but finitely many .)

Comparing Proposition 2 with Proposition 1, it is natural to refer to the function as the Möbius function of the poset; the condition (ii) can then be written as

Proof: If (i) holds, then we have

for any . Iterating this we obtain (ii). Conversely, from (ii) and separating out the term, and grouping all the other terms based on the value of , we obtain (1), and hence (i).

In fact it is not completely necessary that the poset be finite; an inspection of the proof shows that it suffices that every element of the poset has only finitely many predecessors .

It is not difficult to see that Proposition 2 includes Proposition 1 as a special case, after verifying the combinatorial fact that the quantity

is equal to when divides , and vanishes otherwise.

I recently discovered that Proposition 2 can also lead to a useful variant of the inclusion-exclusion principle. The classical version of this principle can be phrased in terms of indicator functions: if are subsets of some set , then

In particular, if there is a finite measure on for which are all measurable, we have

One drawback of this formula is that there are exponentially many terms on the right-hand side: of them, in fact. However, in many cases of interest there are “collisions” between the intersections (for instance, perhaps many of the pairwise intersections agree), in which case there is an opportunity to collect terms and hopefully achieve some cancellation. It turns out that it is possible to use Proposition 2 to do this, in which one only needs to sum over chains in the resulting poset of intersections:

Proposition 3 (Hall-type inclusion-exclusion principle) Let be subsets of some set , and let be the finite poset formed by intersections of some of the (with the convention that is the empty intersection), ordered by set inclusion. Then for any , one has

where are understood to range in . In particular (setting to be the empty intersection) if the are all proper subsets of then we have

In particular, if there is a finite measure on for which are all measurable, we have

Using the Möbius function on the poset , one can write these formulae as

and

Proof: It suffices to establish (2) (to derive (3) from (2) observe that all the are contained in one of the , so the effect of may be absorbed into ). Applying Proposition 2, this is equivalent to the assertion that

for all . But this amounts to the assertion that for each , there is precisely one in with the property that and for any in , namely one can take to be the intersection of all in such that contains .

Example 4 If with , and are all distinct, then we have for any finite measure on that makes measurable that

due to the four chains , , , of length one, and the three chains , , of length two. Note that this expansion just has six terms in it, as opposed to the given by the usual inclusion-exclusion formula, though of course one can reduce the number of terms by combining the factors. This may not seem particularly impressive, especially if one views the term as really being three terms instead of one, but if we add a fourth set with for all , the formula now becomes

and we begin to see more cancellation as we now have just seven terms (or ten if we count as four terms) instead of terms.

Example 5 (Variant of Legendre sieve) If are natural numbers, and is some sequence of complex numbers with only finitely many terms non-zero, then by applying the above proposition to the sets and with equal to counting measure weighted by the we obtain a variant of the Legendre sieve

where range over the set formed by taking least common multiples of the (with the understanding that the empty least common multiple is ), and denotes the assertion that divides but is strictly less than . I am curious to know of this version of the Legendre sieve already appears in the literature (and similarly for the other applications of Proposition 2 given here).

If the poset has bounded depth then the number of terms in Proposition 3 can end up being just polynomially large in rather than exponentially large. Indeed, if all chains in have length at most then the number of terms here is at most . (The examples (4), (5) are ones in which the depth is equal to two.) I hope to report in a later post on how this version of inclusion-exclusion with polynomially many terms can be useful in an application.

Actually in our application we need an abstraction of the above formula, in which the indicator functions are replaced by more abstract idempotents:

Proposition 6 (Hall-type inclusion-exclusion principle for idempotents) Let be pairwise commuting elements of some ring with identity, which are all idempotent (thus for ). Let be the finite poset formed by products of the (with the convention that is the empty product), ordered by declaring when (note that all the elements of are idempotent so this is a partial ordering). Then for any , one has

where are understood to range in . In particular (setting ) if all the are not equal to then we have

Morally speaking this proposition is equivalent to the previous one after applying a “spectral theorem” to simultaneously diagonalise all of the , but it is quicker to just adapt the previous proof to establish this proposition directly. Using the Möbius function for , we can rewrite these formulae as

and

Proof: Again it suffices to verify (6). Using Proposition 2 as before, it suffices to show that

for all (all sums and products are understood to range in ). We can expand

where ranges over all subsets of that contain . For such an , if we write , then is the greatest lower bound of , and we observe that vanishes whenever fails to contain some with . Thus the only that give non-zero contributions to (8) are the intervals of the form for some (which then forms the greatest lower bound for that interval), and the claim (7) follows (after noting that for any ).

Eigenvectors from Eigenvalues: a survey of a basic identity in linear algebra

Peter Denton, Stephen Parke, Xining Zhang, and I have just uploaded to the arXiv a completely rewritten version of our previous paper, now titled “Eigenvectors from Eigenvalues: a survey of a basic identity in linear algebra“. This paper is now a survey of the various literature surrounding the following basic identity in linear algebra, which we propose to call the eigenvector-eigenvalue identity:

Theorem 1 (Eigenvector-eigenvalue identity) Let be an Hermitian matrix, with eigenvalues . Let be a unit eigenvector corresponding to the eigenvalue , and let be the component of . Then

where is the Hermitian matrix formed by deleting the row and column from .

When we posted the first version of this paper, we were unaware of previous appearances of this identity in the literature; a related identity had been used by Erdos-Schlein-Yau and by myself and Van Vu for applications to random matrix theory, but to our knowledge this specific identity appeared to be new. Even two months after our preprint first appeared on the arXiv in August, we had only learned of one other place in the literature where the identity showed up (by Forrester and Zhang, who also cite an earlier paper of Baryshnikov).

The situation changed rather dramatically with the publication of a popular science article in Quanta on this identity in November, which gave this result significantly more exposure. Within a few weeks we became informed (through private communication, online discussion, and exploration of the citation tree around the references we were alerted to) of over three dozen places where the identity, or some other closely related identity, had previously appeared in the literature, in such areas as numerical linear algebra, various aspects of graph theory (graph reconstruction, chemical graph theory, and walks on graphs), inverse eigenvalue problems, random matrix theory, and neutrino physics. As a consequence, we have decided to completely rewrite our article in order to collate this crowdsourced information, and survey the history of this identity, all the known proofs (we collect seven distinct ways to prove the identity (or generalisations thereof)), and all the applications of it that we are currently aware of. The citation graph of the literature that this ad hoc crowdsourcing effort produced is only very weakly connected, which we found surprising:

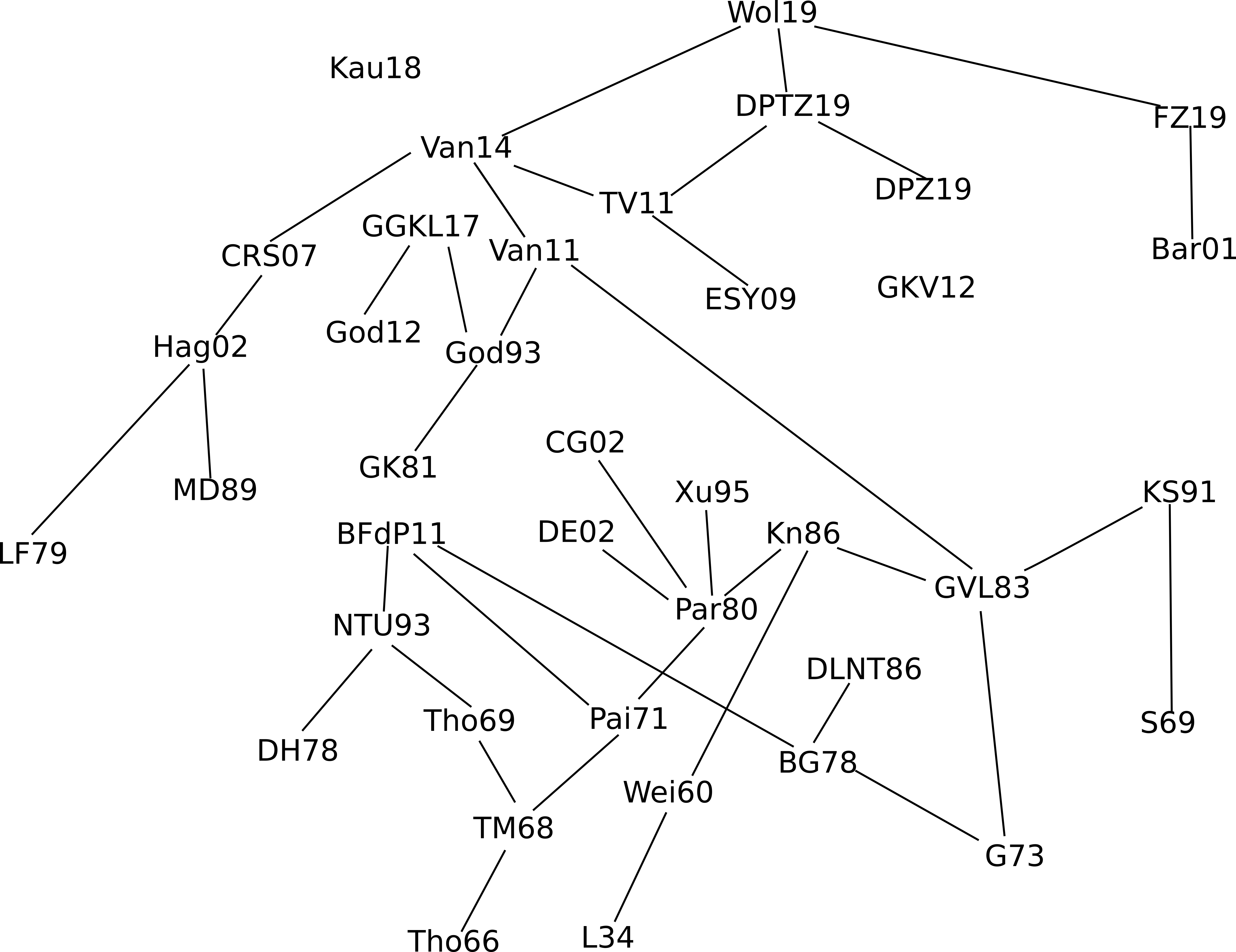
The earliest explicit appearance of the eigenvector-eigenvalue identity we are now aware of is in a 1966 paper of Thompson, although this paper is only cited (directly or indirectly) by a fraction of the known literature, and also there is a precursor identity of Löwner from 1934 that can be shown to imply the identity as a limiting case. At the end of the paper we speculate on some possible reasons why this identity only achieved a modest amount of recognition and dissemination prior to the November 2019 Quanta article.

Eigenvectors from eigenvalues

Peter Denton, Stephen Parke, Xining Zhang, and I have just uploaded to the arXiv the short unpublished note “Eigenvectors from eigenvalues“. This note gives two proofs of a general eigenvector identity observed recently by Denton, Parke and Zhang in the course of some quantum mechanical calculations. The identity is as follows:

Theorem 1 Let be an Hermitian matrix, with eigenvalues . Let be a unit eigenvector corresponding to the eigenvalue , and let be the component of . Then

where is the Hermitian matrix formed by deleting the row and column from .

For instance, if we have

for some real number , -dimensional vector , and Hermitian matrix , then we have

assuming that the denominator is non-zero.

Once one is aware of the identity, it is not so difficult to prove it; we give two proofs, each about half a page long, one of which is based on a variant of the Cauchy-Binet formula, and the other based on properties of the adjugate matrix. But perhaps it is surprising that such a formula exists at all; one does not normally expect to learn much information about eigenvectors purely from knowledge of eigenvalues. In the random matrix theory literature, for instance in this paper of Erdos, Schlein, and Yau, or this later paper of Van Vu and myself, a related identity has been used, namely

but it is not immediately obvious that one can derive the former identity from the latter. (I do so below the fold; we ended up not putting this proof in the note as it was longer than the two other proofs we found. I also give two other proofs below the fold, one from a more geometric perspective and one proceeding via Cramer’s rule.) It was certainly something of a surprise to me that there is no explicit appearance of the components of in the formula (1) (though they do indirectly appear through their effect on the eigenvalues ; for instance from taking traces one sees that ).

One can get some feeling of the identity (1) by considering some special cases. Suppose for instance that is a diagonal matrix with all distinct entries. The upper left entry of is one of the eigenvalues of . If it is equal to , then the eigenvalues of are the other eigenvalues of , and now the left and right-hand sides of (1) are equal to . At the other extreme, if is equal to a different eigenvalue of , then now appears as an eigenvalue of , and both sides of (1) now vanish. More generally, if we order the eigenvalues and , then the Cauchy interlacing inequalities tell us that

for , and

for , so that the right-hand side of (1) lies between and , which is of course consistent with (1) as is a unit vector. Thus the identity relates the coefficient sizes of an eigenvector with the extent to which the Cauchy interlacing inequalities are sharp.

Conversions between standard polynomial bases

(This post is mostly intended for my own reference, as I found myself repeatedly looking up several conversions between polynomial bases on various occasions.)

Let denote the vector space of polynomials of one variable with real coefficients of degree at most . This is a vector space of dimension , and the sequence of these spaces form a filtration:

A standard basis for these vector spaces are given by the monomials : every polynomial in can be expressed uniquely as a linear combination of the first monomials . More generally, if one has any sequence of polynomials, with each of degree exactly , then an easy induction shows that forms a basis for .

In particular, if we have two such sequences and of polynomials, with each of degree and each of degree , then must be expressible uniquely as a linear combination of the polynomials , thus we have an identity of the form

for some change of basis coefficients . These coefficients describe how to convert a polynomial expressed in the basis into a polynomial expressed in the basis.

Many standard combinatorial quantities involving two natural numbers can be interpreted as such change of basis coefficients. The most familiar example are the binomial coefficients , which measures the conversion from the shifted monomial basis to the monomial basis , thanks to (a special case of) the binomial formula:

thus for instance

More generally, for any shift , the conversion from to is measured by the coefficients , thanks to the general case of the binomial formula.

But there are other bases of interest too. For instance if one uses the falling factorial basis

then the conversion from falling factorials to monomials is given by the Stirling numbers of the first kind :

thus for instance

and the conversion back is given by the Stirling numbers of the second kind :

thus for instance

If one uses the binomial functions as a basis instead of the falling factorials, one of course can rewrite these conversions as

and

thus for instance

and

As a slight variant, if one instead uses rising factorials

then the conversion to monomials yields the unsigned Stirling numbers of the first kind:

thus for instance

One final basis comes from the polylogarithm functions

For instance one has

and more generally one has

for all natural numbers and some polynomial of degree (the Eulerian polynomials), which when converted to the monomial basis yields the (shifted) Eulerian numbers

For instance

These particular coefficients also have useful combinatorial interpretations. For instance:

• The binomial coefficient is of course the number of -element subsets of .
• The unsigned Stirling numbers of the first kind are the number of permutations of with exactly cycles. The signed Stirling numbers are then given by the formula .
• The Stirling numbers of the second kind are the number of ways to partition into non-empty subsets.
• The Eulerian numbers are the number of permutations of with exactly ascents.

These coefficients behave similarly to each other in several ways. For instance, the binomial coefficients obey the well known Pascal identity

(with the convention that vanishes outside of the range ). In a similar spirit, the unsigned Stirling numbers of the first kind obey the identity

and the signed counterparts obey the identity

The Stirling numbers of the second kind obey the identity

and the Eulerian numbers obey the identity

Word maps close to the identity

While talking mathematics with a postdoc here at UCLA (March Boedihardjo) we came across the following matrix problem which we managed to solve, but the proof was cute and the process of discovering it was fun, so I thought I would present the problem here as a puzzle without revealing the solution for now.

The problem involves word maps on a matrix group, which for sake of discussion we will take to be the special orthogonal group of real matrices (one of the smallest matrix groups that contains a copy of the free group, which incidentally is the key observation powering the Banach-Tarski paradox).  Given any abstract word of two generators and their inverses (i.e., an element of the free group ), one can define the word map simply by substituting a pair of matrices in into these generators.  For instance, if one has the word , then the corresponding word map is given by

for .  Because contains a copy of the free group, we see the word map is non-trivial (not equal to the identity) if and only if the word itself is nontrivial.

Anyway, here is the problem:

Problem. Does there exist a sequence of non-trivial word maps that converge uniformly to the identity map?

To put it another way, given any , does there exist a non-trivial word such that for all , where denotes (say) the operator norm, and denotes the identity matrix in ?

As I said, I don’t want to spoil the fun of working out this problem, so I will leave it as a challenge. Readers are welcome to share their thoughts, partial solutions, or full solutions in the comments below.