Today, Prof. Margulis continued his lecture series, focusing on two specific examples of homogeneous dynamics applications to number theory, namely counting lattice points on algebraic varieties, and quantitative versions of the Oppenheim conjecture. (Due to lack of time, the third application mentioned in the previous lecture, namely metric theory of Diophantine approximation, was not covered.)
— Counting lattice points in algebraic varieties —
Let be an algebraic variety defined over
. In general, the question of counting the lattice points
is pretty much intractible (even determining whether
is non-empty is essentially Hilbert’s tenth problem, known to be undecidable by Matiyasevich’s theorem). However, the problem looks much more tractable if V is homogeneous, in the sense that there exists a reductive subgroup G of
, defined over
, which preserves V and acts transitively on V (thus
for some
). A general question here would be to determine the asymptotics of the quantity
as
, where
is the number of lattice points in V in the ball TB of radius T.
Thanks to a classical theorem of Borel and Harish-Chandra, it is known in the above setting that the integer points of V split as the finite union of orbits of the discrete group
. So, modulo the problem of effectively computing these orbts (which is admittedly a non-trivial task), the question boils down to obtaining asymptotics for
as
for some orbit
for some
.
Naively, one expects a discrete count such as to asymptotically resemble its continuous counterpart (much as, say, the number of lattice points in a ball of radius R is known by elementary volume packing arguments going back to Gauss to asymptotically be equivalent to the volume of that ball). In this setting, the intuition would be formalised as follows. We can express the homogeneous space V as
, where H is the stabiliser of
. Then we can pull back
to
to create the ball-like region
. Also, making the mild assumption that the connected component
of G, H (where connectedness is in the algebraic geometry sense) have no non-trivial characters over
(this hypothesis is automatic when G is semisiple), it follows from the work of Borel and Harish-Chandra that the homogeneous space
, and the subspace
both support invariant probability measures
, which in turn naturally define an invariant measure
on G/H. The natural “discrete count is asymptotically equivalent to continuous count” conjecture would then be the assertion that
(1)
where means that
as
.
In principle, the computation of the continuous volume is “just” a computation of a several variable calculus integral, and so (1) provides an asymptotic for the growth of lattice points in the orbit
.
A significant result in this subject is the work of Eskin, Mozes, and Shah, who showed that the asymptotic (1) held under the assumption that is a maximal proper connected
-subgroup of G. The key step in their argument is to show that for any sequence
going to infinity, that the translated measures
converge weakly to
(i.e. become asymptotically equidistributed).
As a typical illustration of their results, consider the variety
of integer matrices with a fixed characteristic polynomial p, which should of course be monic of degree n and with integer coefficients. We will also take and assume p irreducible. Then as a corollary of the general theorem of Eskin, Mozes, and Shah,
is asymptotically
, where
is explicitly computable in terms of various algebraic number theory data arising from p. For instance, if p splits over
and has a root
such that
is the ring of integers in
, then
where D is the discriminant of p, R is the regulator of ,
is the volume of the d-dimensional unit ball, h is the class number of
, and
is a variant of the Riemann Xi function.
— Quantitative Oppenheim conjecture —
For the setting of the quantitative Oppenheim conjecture, one considers an indefinite quadratic form with some signature
for some p+q=n; we normalise
, and also normalise Q to have discriminant 1. We also fix a star-shaped region
around the origin (one can just take
to be the unit ball for sake of concreteness) and consider for fixed
, the discrete quantity
and the continuous quantity
.
Again, can be computed asymptotically, indeed it is not hard (basically just several variable calculus) to show that
where is the explicit quantity
where L is the light cone of Q, and A is the area element.
In analogy with (1) and with the Gauss circle problem, we would expect
(2)
for each fixed Q, , a, b. The usual volume packing argument does not work in the indefinite case because the set
is very “narrow”. Nevertheless, from the work of Dani and Margulis we have some results. Firstly, when Q is irrational and
, we have the lower bound
, (3)
thus there are asymptotically at least as many lattice points as predicted by (2). This bound is uniform over any compact set of irrational forms Q. In the case , we also have the bound
uniformly in and for Q in a compact set (and not necessarily irrational), where c depends only on this compact set and on
. (The condition
is necessary here, since otherwise the counterexamples to Meyer’s theorem in lower dimensions give examples when
stays bounded while
goes to infinity.)
A more recent result of Eskin, Margulis, and Mozes improves the lower bound (3) to the asymptotic (2) in the case when and Q is irrational. This leaves out the “exceptional” cases
. Perhaps surprisingly, the asymptotic (2) fails in such cases, in fact there are examples of forms Q in which
grows close to logarithmically in T. (More precisely, given any function
, there exists a form Q and a sequence of times
such that
.) The forms are actually quite explicit; in the
case they are given by
where
is very well approximated by rationals, and in the case
the are of the form
for similar
. (These sorts of examples originate with an observation of Sarnak.) In the above paper it was shown that the (2,2) counterexamples given here are “essentially” the “only” counterexamples of this signature, although the precise formal statement of this type is technical. The situation for (2,1) signature remains somewhat unclear. On the other hand, it is not too difficult to show that for generic Q (in particular, for almost every Q), one recovers the asymptotic (2). And for every Q in a given compact set K, there is a universal upper bound
in the non-exceptional cases
, with a logarithmic correction
in the exceptional cases
.
One reason for the failure of the asymptotic in these exceptional cases can apparently be traced back to the refusal of a certain integral to decay in the limit . Specifically, if one lets
be the unit circle in the standard light cone
, then it is a pleasant geometric exercise to observe that the integral
for
is in fact independent of g, and in particular does not go to zero as
, whereas the higher-dimensional analogues of this integral do decay.
One of the basic tools in proving these estimates is the Siegel transform, which maps absolutely integrable functions to absolutely integrable functions
by the formula
.
A classical observation of Siegel is that this transform is mass-preserving:
.
As a quick corollary, one recovers a classical theorem of Minkowski that any measurable subset A of of measure less than 1 is avoided by at least one unimodular lattice (just apply the above identity with
). It turns out that one needs a variant of this statement, namely that the proportion of lattices which avoid A has measure
. For this one needs some second moment estimates on
, which turn out to be classical (essentially going back to C. C. Rogers) for
) but are quite delicate for n=2, requiring in particular some facts about Eisenstein series and which were first worked out by Athreya and Margulis.
Using Siegel’s identity, one can reduce matters to understanding how the transform of a function f equidistributes over a shifted orbit
in
as
, where
is a one-parameter subgroup of
fixing Q,
,
is a compact subgroup of G, and the lattice
is fixed. (Concretely, one can take
,
to be the Lorentz boost that maps
to
and
to
, but leaves the other basis vectors
unchanged, and
is the stabiliser of
.
If was continuous and bounded, then the question is purely a dynamical one, involving how the orbit
equidistributes in
. Unfortunately
blows up when the lattice
approaches degeneracy, in the sense that there exists some intermediate dimension parallelopiped in the lattice of small measure. (Thus, for instance, one way one can degenerate is if one of the vectors of
approaches the origin.) This is formalised by a classical “Lipschitz principle”, bounding
by
for some geometric function
on
(essentially the reciprocal of the least measure of an parallelopiped in the lattice). To deal with this blowup, one basically needs some moment estimates on
in the cusp of
. In the non-exceptional case
, it turns out that one can get bounds on the moments
for any
, and in particular for some exponent s larger than 1, and this is enough to ignore the effect of the cusp. But in the exceptional case
one can only get moment estimates for
, which is not sufficient; but one has a substitute bound on
in this case which is enough to give control up to a
factor.

5 comments
Comments feed for this article
13 July, 2011 at 6:44 am
Conférence internationale Géométrie Ergodique (Orsay 2011) I « Disquisitiones Mathematicae
[…] mentioned above, I strongly recommend reading Terence Tao’s posts on this subject, specially these ones […]
2 July, 2012 at 8:40 am
Rex
How do we prove that the Siegel transform is mass-preserving?
Also, do you know of any standard references about this operator?
2 July, 2012 at 9:17 am
Terence Tao
See K.L. Siegel, Lectures on the Geometry of Numbers, Springer-Verlag, New York, 1989. One can, if one wishes, interpret Siegel’s formula as a definition of Haar measure on the quotient space , at which point the only issue is to verify that the measure is invariant and has total mass 1.
, at which point the only issue is to verify that the measure is invariant and has total mass 1.
3 July, 2012 at 6:52 am
Rex
Why does the sum over lattice points in the definition of exclude the origin?
exclude the origin?
Is this just some kind of convention, or is there an important reason why we cannot add into the sum?
into the sum?
3 July, 2012 at 7:42 am
Terence Tao
Well, the mass formula would fail then, since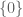 has measure zero in
has measure zero in  but would give a non-zero contribution on the
but would give a non-zero contribution on the 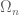 side.
side.
Note that the action of on
on  has two orbits. One is
has two orbits. One is 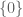 , and the other is
, and the other is  . Generally speaking, formulae in dynamics are cleaner if restricted to one orbit (or one orbit closure, or an ergodic measure) rather than a combination of such orbits.
. Generally speaking, formulae in dynamics are cleaner if restricted to one orbit (or one orbit closure, or an ergodic measure) rather than a combination of such orbits.