Well, participation in the IMO 2009 Q6 polymath project has exceeded my expectations; it appears that the collaborative effort has scored some partial successes toward a solution in the first 24 hours of its existence, but is not quite there yet.
As the thread has become overly long, I am following established polymath practice and starting a new thread here, hopefully to try to impose more order onto the chaos. In order to assist this effort, some of the participants may wish to summarise some of the “state of play” so far. (I am unable to do this due to being biased by the knowledge of a solution.)
The comment numbering system has not worked as smoothly as I had hoped, but it is still better than nothing. I propose that comments in this thread start at 200, so as not to collide with the previous thread.
Of course, all the rules of the polymath exercise (as discussed in the previous thread) continue to apply. I am pleased to see that virtually everyone participating has adhered to the collaborative spirit of the exercise, for instance in keeping criticism constructive and technical rather than pejorative and personal.
As an experiment, I have enabled one level of comment threading; thus one can reply to a specific comment in the thread below. If one does so, I would request that you number the comment by subsection, for instance the first response to comment 234 would be numbered 234.1, the next one 234.2, and so forth. There is a tradeoff here; the threading adds more structure to the comments, but the flip side of this is that it makes it harder to read off at a glance all the comments made since the last time one checks the thread. Hopefully participants will be able to use their discretion when to reply and when not to. [Update, Jul 21: Threading should work properly now, I didn’t set it properly before.]

172 comments
Comments feed for this article
25 July, 2009 at 9:27 am
Mark Bennet
I wonder if there are equivalent formulations. Here is one which is not so general as the original, but might be more confusing to solve.
A round table has n(n+1)/2 seats. n boys come in and discover that there are already (n-1) girls sitting at the table. Show that the boys can always arrange to sit down at vacant seats so that the distances between consecutive boys are all different.
26 July, 2009 at 4:00 am
Mark Bennet
Actually there may be proof strategies which are easier in the circular case (identifying the beginning and end of the path) if the grasshopper can start at any vacant space.
For example, the ‘mod n’ kind of proof – there is a residue class completely unused – promises to work quite straightforwardly with this set up.
And there may be counting approaches which benefit from the extra symmetry of the circle.
25 July, 2009 at 11:15 am
wenwen
I’ve a proof which seems to be correct. I don’t know if it appeared in the above discussions.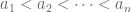 be the
be the  given positive integers.
given positive integers.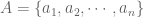 and
and 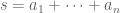 .
. be
be 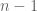 numbers the the grasshopper wants to avoid.
numbers the the grasshopper wants to avoid. .
.
Let
Denote
Let
Denote
Induction on . When n = 1,2,3, it's easy to check.
. When n = 1,2,3, it's easy to check. , it's true. We want to show that for
, it's true. We want to show that for  , it's true.
, it's true.
Assume now for
Case I.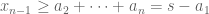
There exists a , such that
, such that 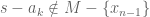 . So for the pair
. So for the pair  we can use the induction hypothesis to get permutation of
we can use the induction hypothesis to get permutation of 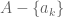 , say
, say 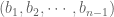 to avoid the set
to avoid the set 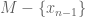 . Since
. Since 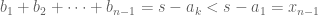 , so the permutation
, so the permutation 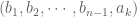 of
of  is good.
is good.
Case II.
Consider the pair , by the condition, we know that we can use the induction hypothesis to have one permutation of
, by the condition, we know that we can use the induction hypothesis to have one permutation of  , say
, say 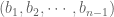 to avoid the set
to avoid the set 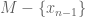 . If for any partial sum
. If for any partial sum 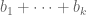 , it's NOT equal to
, it's NOT equal to  , the permutation
, the permutation  is what we want; if there is a $k$, such that
is what we want; if there is a $k$, such that 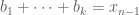 , we switch
, we switch  and
and 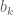 to get the following permutation
to get the following permutation  , it works since this switch provides a big jump to avoid every thing at the
, it works since this switch provides a big jump to avoid every thing at the 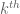 step.
step.
CaseIII.
In this case there must be a $1<k<n$, such that
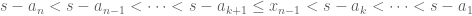
We first claim that we can require for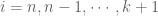 , we have
, we have 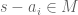 .(otherwise, if
.(otherwise, if  , we consider the pair
, we consider the pair 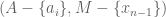 to get a permutation
to get a permutation 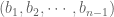 of
of 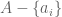 , and take
, and take 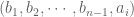 as the permutation we need.)
as the permutation we need.)
Now consider the set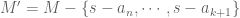 and it has exactly
and it has exactly 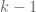 elements, so there is a
elements, so there is a  , such that
, such that 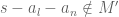 . We consider the pair
. We consider the pair  , it easy to see that we can use the induction hypothesis on this set to get a permutation
, it easy to see that we can use the induction hypothesis on this set to get a permutation 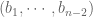 of
of 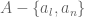 , then we can take the permutation
, then we can take the permutation  for
for  .
.
25 July, 2009 at 4:26 pm
Luka Lasic
@wenwen Case I. wonderful, Case II. wonderful,
Case III. wonderful long jump.
Change cases (1,2,3) -> (3,1,2), and X -> M.
26 July, 2009 at 7:37 am
Luka Lasic
PROBLEM {0,1,2} :
O:={0} and splits are: 0 -> (1,2) and 0->(2,1) and 1->(0,2) and 1->(2,0) and 2->(0,1) and 2->(1,0). Now:
A={(1,2),(2,1)}, and splits on first coordinates leads to:
1[A]={(0,2,2),(2,0,2),(0,1,1),(1,0,1)}, and splits on second coordinates leads to:
2[A]={(1,0,1),(1,1,0),(2,0,2),(2,2,0)}. Clearly, intersection of 1[A] and 2[A] are non-empty.
Recursively, 1[1[A]], 2[1[A]], 3[1[A]], 1[2[A]], 2[2[A]], 3[2[A]],
are pairwise with non-empty intersection, and analogous to infinity.
29 July, 2009 at 6:08 am
Gil Kalai
As some sort of control experiment I asked A. Nili and got this reply (I am not sure if it is identical to argument that was already presented):
Problem:
let a_1,a_2,…,a_n be n distinct positive real numbers,
and let b_1,b_2,…,b_{n-1} be n-1 distinct positive reals.
Prove that there is a permutation a_{i1},a_{i2},…,a_{in} of the
numbers a_i so that all initial sums a_{i1}+a_{i2}+…+a_{ij}
differ from all b_k’s.
Solution:
Proof by induction on n. Trivial for n=1, assuming for n-1, omit
the largest a and the largest b. By induction the remaining a’s can
be arranged so that their initial sums avoid all b’s but possibly
the largest. If the largest is obtained as
a_{i1}+a_{i2}+…+a_{ij}, replace a_{ij} by a_max and put a_{ij}
last (or anywhere after a_max), noting that all initial sums of
at least j a’s are now larger than the largest b.
29 July, 2009 at 6:58 am
Kristal Cantwell
“Proof by induction on n. Trivial for n=1, assuming for n-1, omit
the largest a and the largest b. By induction the remaining a’s can
be arranged so that their initial sums avoid all b’s but possibly
the largest. If the largest is obtained as”
the sum of the n-1 elements could also be a landmine in the n-1 case we don’t prove it we have it by hypothesis here we have the sum of n elements cannot be a mine by hypothesis.
In my
24 July, 2009 8:10 am proof I go along those lines and then I have to deal with the n-1 elements issue mentioned above. It can be dealt with. I think it is the fifth proof on the wiki.
29 July, 2009 at 7:58 am
Alex and Ecki
This is the easier part 1 of the proof 5 already in the wiki.
30 July, 2009 at 12:44 am
Gil
Hmm, right. I overlooked that…
2 August, 2009 at 9:33 am
A mini-polymath project « Euclidean Ramsey Theory
[…] https://terrytao.wordpress.com/2009/07/21/imo-2009-q6-mini-polymath-project-cont/ […]
7 August, 2009 at 9:49 am
E
Sadly I only got to see this problem today and it is seems hopeless to follow the discussion.
I was following a first lead on the problem sitting on my coach which seemed to me like a good one.
I would be happy to hear if this direction was discussed and what you guys think.
Let us first notice that since all the jumps are of distinct size we have n! different ways in which our grasshopper can take his course.
Secondly, a simple observation is that we must have at least two completely distinct paths since if we don’t then we can take an arbitrary path and choose our mines to match it exactly, by the assumption we’ve just made, any other path has at least one step that matches the first path and the theorem is disproven(sorry for my shaky English).
So we now know that we must have atleast two completely distinct possible paths. Obviously showing that we actually got two such paths proves the theorem.
Again, if we assume that we do not have such two paths, than every two paths have atleast one point in common, and with some simple combinatorics it is eazy to see that we get less than the N! possible different paths that we know exist.
My bet is that i’m missing something here. It took me less than an hour to come up with this “solution” while many people whos math talent and experience are superior to mine seem to have struggled with the problem.
BTW, did the discussion move somewhere else or something like that?
7 August, 2009 at 10:01 am
E
Okay, I was too hasty
“Obviously showing that we actually got two such paths proves the theorem.”
11 August, 2009 at 6:05 am
JM
Another solution, I think.
Let’s suppose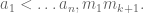
We make an observation: If we get up to or past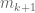 with
with  steps, then the
steps, then the
 -th step lands on a mine. (To see this, let
-th step lands on a mine. (To see this, let  be the steps
be the steps We can find a jump sequence clearing
We can find a jump sequence clearing 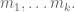 This jump sequence in fact avoids all mines: With
This jump sequence in fact avoids all mines: With 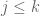 steps we can
steps we can ; the
; the  -th step doesnt land on a
-th step doesnt land on a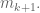 This allows us to construct a mine free trip for the original
This allows us to construct a mine free trip for the original
 , which we aren’t supposed to be able to.)
, which we aren’t supposed to be able to.)
with
only trip up on one of the mines
mine and goes past
Set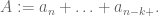 By considering
By considering 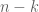 numbers
numbers 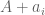 with
with 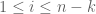 , the observation above tells us that there exists
, the observation above tells us that there exists 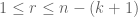
 Of course, we also have those
Of course, we also have those 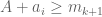 are in
are in 
with
Now consider the following numbers all
numbers all  :
:  and
and 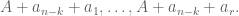 We can conclude that
We can conclude that 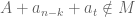 for some
for some 
We now use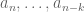 and
and  to jump
to jump 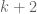 steps clearing
steps clearing  and
and 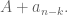 This trip doesn't land on any mine: if it did, it can
This trip doesn't land on any mine: if it did, it can -th step (anything before, distance covered is
-th step (anything before, distance covered is 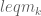 ). On the
). On the
 -th step it must land on
-th step it must land on 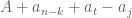 for some
for some 

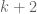 steps going safely beyond
steps going safely beyond  ,
,
only be on the
But then
So we have in fact a mine free trip of
which allows us to construct a solution for the original problem.
That proves the claim.
To finish off, by the claim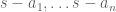 are all
are all 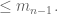 So we must
So we must We use jumps apart from
We use jumps apart from  to go clear mines upto
to go clear mines upto 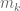 and round off with
and round off with 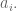
have
12 August, 2009 at 1:23 am
JM
Apart from the formatting problems, couple of paragraphs seem to have disappeared since my writing and it appearing. The solution should begin with:
Let’s suppose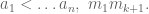
The soln still doesnt read well, but hopefully there is enough explanation for one to work through.
12 August, 2009 at 1:31 am
JM
Still doesnt work; last try before I give up :)
Let’s suppose a_1 < \ldots a_n, m_1 < … m_{k+1}.
12 August, 2009 at 6:23 am
Terence Tao
I think what is happening is that the parser is interpreting your < and > signs as HTML. One can fix this by using < and > instead. Alternatively, you can place your solution on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=Imo_2009_q6
17 October, 2009 at 3:42 am
Rajen Shah
I’m not sure if I’m missing something here:
There are n! different paths that could be taken (if we forget the restriction imposed by the set M).
Each element of M which is a sum of k numbers from a_1 up to a_n blocks out k!(n-k)! of these paths.
Now if we count up the maximum possible number of paths blocked, it is easy to see we can never block more than n! paths.
Does this not work?
17 October, 2009 at 4:46 am
Spencer
Hi Rajen,
I haven’t thought about the problem seriously myself but I don’t think that your observation provides a solution unless the sums formed from the a_i’s happen to all be distinct.
‘Coincidences’ between the sums will make it harder. For example, if the first few of the a_i are 3,4,6 and 7, then a mine at 10 = 3 + 7 = 4 + 6, blocks more paths than you have accounted for.
21 February, 2010 at 8:44 am
Bài toán số 6 trong IMO 2009 « Sharing
[…] link 3 […]
17 June, 2010 at 10:40 pm
Mark Bennet
Here is a non-technical version of an early solution, developed for use with a school group.
If n=1 there is one jump and no mines. Easy.
Assume cases up to n-1 are done.
Try to make the longest jump from the left hand side.
Case A: this jump clears at least one mine and lands on an unmined place. Thene the remainder is case n-1 and we are done.
Case B: the longest jump clears no mines, though it may land on one. Remove the leftmost mine, and take out the longest jump. Working from the right, now, we have a case of (n-1) and can make all the leaps in some order, clearing all the remaining mines.
Put back the leftmost mine.
If no jump lands on it, then we can add the longest jump at the left hand end, and we are done.
If a jump does land on it, then working from the right, replace that jump with the longest jump. Now up to the longest jump we have cleared all the mines and the remaining jumps can be added at the left hand end in any order to complete the task.
Case C: the longest jump clears at least one mine, but lands on a mine – so there is a mine at distance equal to the longest jump from the left hand end, with at least one mine to the left of this. Then any combination of two jumps from the left hand end and including the longest will clear at least two mines.
Consider the n-1 possibilities (from the left) of {short jump followed by longest jump}. None of these lands on the mine whose fixed position is known – so there are just n-2 more mines to avoid. Because the short jumps are all different lengths, all the positions landed on by this set of n-1 pairs are distinct. n-2 mines can only block n-2 of these possibilities, so there is at least one pair {short jump followed by longest jump} which does not land on a mine and which clears at least two mines. The rest is case n-2 and we are done.
15 August, 2010 at 3:30 pm
noname
I found a solution but it seems too much simple compared to other solutions so please let me know if I made a mistake.
Let S={A_1,…,A_n+1} and T={B_1,…,B_n}
Suppose the statement is true for n. We will prove it for n+1.
Let a k-sum to be sum of k elements of S. Now there are n+1 n-sums and each one is different from one other because elements of S assumed to be distinct. So at least one of the n-sums is not an element of T. Let A_k is not in this n-sum. Apply the statement for S/A_k and T/B_n . Grasshopper doesn’t land on any mine including B_n. By adding this order A_k we prove the statement.