In harmonic analysis and PDE, one often wants to place a function on some domain (let’s take a Euclidean space
for simplicity) in one or more function spaces in order to quantify its “size” in some sense. Examples include
- The Lebesgue spaces
of functions
whose norm
is finite, as well as their relatives such as the weak
spaces
(and more generally the Lorentz spaces
) and Orlicz spaces such as
and
;
- The classical regularity spaces
, together with their Hölder continuous counterparts
;
- The Sobolev spaces
of functions
whose norm
is finite (other equivalent definitions of this norm exist, and there are technicalities if
is negative or
), as well as relatives such as homogeneous Sobolev spaces
, Besov spaces
, and Triebel-Lizorkin spaces
. (The conventions for the superscripts and subscripts here are highly variable.)
- Hardy spaces
, the space BMO of functions of bounded mean oscillation (and the subspace VMO of functions of vanishing mean oscillation);
- The Wiener algebra
;
- Morrey spaces
;
- The space
of finite measures;
- etc., etc.
As the above partial list indicates, there is an entire zoo of function spaces one could consider, and it can be difficult at first to see how they are organised with respect to each other. However, one can get some clarity in this regard by drawing a type diagram for the function spaces one is trying to study. A type diagram assigns a tuple (usually a pair) of relevant exponents to each function space. For function spaces on Euclidean space, two such exponents are the regularity
of the space, and the integrability
of the space. These two quantities are somewhat fuzzy in nature (and are not easily defined for all possible function spaces), but can basically be described as follows. We test the function space norm
of a modulated rescaled bump function
(1)
where is an amplitude,
is a radius,
is a test function,
is a position, and
is a frequency of some magnitude
. One then studies how the norm
depends on the parameters
. Typically, one has a relationship of the form
(2)
for some exponents , at least in the high-frequency case when
is large (in particular, from the uncertainty principle it is natural to require
, and when dealing with inhomogeneous norms it is also natural to require
). The exponent
measures how sensitive the
norm is to oscillation, and thus controls regularity; if
is large, then oscillating functions will have large
norm, and thus functions in
will tend not to oscillate too much and thus be smooth. Similarly, the exponent
measures how sensitive the
norm is to the function
spreading out to large scales; if
is small, then slowly decaying functions will have large norm, so that functions in
tend to decay quickly; conversely, if
is large, then singular functions will tend to have large norm, so that functions in
will tend to not have high peaks.
Note that the exponent in (2) could be positive, zero, or negative, however the exponent
should be non-negative, since intuitively enlarging
should always lead to a larger (or at least comparable) norm. Finally, the exponent in the
parameter should always be
, since norms are by definition homogeneous. Note also that the position
plays no role in (1); this reflects the fact that most of the popular function spaces in analysis are translation-invariant.
The type diagram below plots the indices of various spaces. The black dots indicate those spaces for which the
indices are fixed; the blue dots are those spaces for which at least one of the
indices are variable (and so, depending on the value chosen for these parameters, these spaces may end up in a different location on the type diagram than the typical location indicated here).
(There are some minor cheats in this diagram, for instance for the Orlicz spaces and
one has to adjust (1) by a logarithmic factor. Also, the norms for the Schwartz space
are not translation-invariant and thus not perfectly describable by this formalism. This picture should be viewed as a visual aid only, and not as a genuinely rigorous mathematical statement.)
The type diagram can be used to clarify some of the relationships between function spaces, such as Sobolev embedding. For instance, when working with inhomogeneous spaces (which basically identifies low frequencies with medium frequencies
, so that one is effectively always in the regime
), then decreasing the
parameter results in decreasing the right-hand side of (1). Thus, one expects the function space norms to get smaller (and the function spaces to get larger) if one decreases
while keeping
fixed. Thus, for instance,
should be contained in
, and so forth. Note however that this inclusion is not available for homogeneous function spaces such as
, in which the frequency parameter
can be either much larger than
or much smaller than
.
Similarly, if one is working in a compact domain rather than in , then one has effectively capped the radius parameter
to be bounded, and so we expect the function space norms to get smaller (and the function spaces to get larger) as one increases
, thus for instance
will be contained in
. Conversely, if one is working in a discrete domain such as
, then the radius parameter
has now effectively been bounded from below, and the reverse should occur: the function spaces should get larger as one decreases
. (If the domain is both compact and discrete, then it is finite, and on a finite-dimensional space all norms are equivalent.)
As mentioned earlier, the uncertainty principle suggests that one has the restriction . From this and (2), we expect to be able to enlarge the function space by trading in the regularity parameter
for the integrability parameter
, keeping the dimensional quantity
fixed. This is indeed how Sobolev embedding works. Note in some cases one runs out of regularity before p goes all the way to infinity (thus ending up at an
space), while in other cases p hits infinity first. In the latter case, one can embed the Sobolev space into a Holder space such as
.
On continuous domains, one can send the frequency off to infinity, keeping the amplitude
and radius
fixed. From this and (1) we see that norms with a lower regularity
can never hope to control norms with a higher regularity
, no matter what one does with the integrability parameter. Note however that in discrete settings this obstruction disappears; when working on, say,
, then in fact one can gain as much regularity as one wishes for free, and there is no distinction between a Lebesgue space
and their Sobolev counterparts
in such a setting.
When interpolating between two spaces (using either the real or complex interpolation method), the interpolated space usually has regularity and integrability exponents on the line segment between the corresponding exponents of the endpoint spaces. (This can be heuristically justified from the formula (2) by thinking about how the real or complex interpolation methods actually work.) Typically, one can control the norm of the interpolated space by the geometric mean of the endpoint norms that is indicated by this line segment; again, this is plausible from looking at (2).
The space is self-dual. More generally, the dual of a function space
will generally have type exponents that are the reflection of the original exponents around the
origin. Consider for instance the dual spaces
or
in the above diagram.
Spaces whose integrability exponent is larger than 1 (i.e. which lie to the left of the dotted line) tend to be Banach spaces, while spaces whose integrability exponent is less than 1 are almost never Banach spaces. (This can be justified by covering a large ball into small balls and considering how (1) would interact with the triangle inequality in this case). The case
is borderline; some spaces at this level of integrability, such as
, are Banach spaces, while other spaces, such as
, are not.
While the regularity and integrability
are usually the most important exponents in a function space (because amplitude, width, and frequency are usually the most important features of a function in analysis), they do not tell the entire story. One major reason for this is that the modulated bump functions (1), while an important class of test examples of functions, are by no means the only functions that one would wish to study. For instance, one could also consider sums of bump functions (1) at different scales. The behaviour of the function space norms on such spaces is often controlled by secondary exponents, such as the second exponent
that arises in Lorentz spaces, Besov spaces, or Triebel-Lizorkin spaces. For instance, consider the function
, (3)
where is a large integer, representing the number of distinct scales present in
. Any function space with regularity
and
should assign each summand
in (3) a norm of O(1), so the norm of
could be as large as
if one assumes the triangle inequality. This is indeed the case for the
norm, but for the weak
norm, i.e. the
norm,
only has size
. More generally, for the Lorentz spaces
,
will have a norm of about
. Thus we see that such secondary exponents can influence the norm of a function by an amount which is polynomial in the number of scales. In many applications, though, the number of scales is a “logarithmic” quantity and thus of lower order interest when compared against the “polynomial” exponents such as
and
. So the fine distinctions between, say, strong
and weak
, are only of interest in “critical” situations in which one cannot afford to lose any logarithmic factors (this is for instance the case in much of Calderon-Zygmund theory).
We have cheated somewhat by only working in the high frequency regime. When dealing with inhomogeneous spaces, one often has a different set of exponents for (1) in the low-frequency regime than in the high-frequency regime. In such cases, one sometimes has to use a more complicated type diagram to genuinely model the situation, e.g. by assigning to each space a convex set of type exponents rather than a single exponent, or perhaps having two separate type diagrams, one for the high frequency regime and one for the low frequency regime. Such diagrams can get quite complicated, and will probably not be much use to a beginner in the subject, though in the hands of an expert who knows what he or she is doing, they can still be an effective visual aid.


33 comments
Comments feed for this article
11 March, 2010 at 11:51 pm
kunal
Nice post.
“…so we expect the function space norms to get smaller (and the function spaces to get larger) as one increases 1/p…”
– I guess what was meant is that “as one increases p”.
A similar typo is there for the sequence spaces, immediately after this line.
12 March, 2010 at 1:23 pm
Terence Tao
Actually, I believe the inclusions are correct as they stand. (Increasing 1/p is of course equivalent to decreasing p.) Note that the norms and the spaces go in different directions; making the norms smaller causes the spaces to become larger, and vice versa.
For historical reasons p is the exponent used to denote integrability, but in many ways 1/p is in fact the more natural quantity (particularly with regard to interpolation and dimensional analysis).
12 March, 2010 at 4:00 pm
mathchief
“Thus, one expects the function space norms to get smaller (and the function spaces to get larger) if one decreases s while keeping p fixed. Thus, for instance, W^{k,p} should contain W^{k-1,p}”
I think it should be the reverse way right? since decrease s by 1, therefore the norms gets smaller, the function may have W^{k,p} norm equal to \infty but has a finite W^{k-1,p} norm
[Corrected, thanks. Ironic that I had to do this after cautioning against precisely this confusion – T.]
12 March, 2010 at 4:02 pm
mathchief
BTW really nice article, the visualization of different spaces is so awesome, IMHO every analysis book should add the graph whenever introducing the function spaces lol
13 March, 2010 at 8:26 am
Jonathan Vos Post
Although two dimensional, the diagram is not a “periodic table” — yet is just as useful and illuminating! Great organizational and explanatory thread.
13 March, 2010 at 2:22 pm
anonymous
Really cool diagram Terry, thank you! I’m thinking about a 3-D version where the horizontal axes are 1/p and 1/q. This will help better visualize those spaces that depend on two integrability parameters. The third axis would still be smoothness. I’d also add modulation spaces into the mix, which fit nicely in your exposition too. Thanks again!
29 December, 2020 at 3:42 am
Anonymous
Very interesting diagram!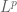 spaces,
spaces,  provides a nice algebra, with the usual pointwise multiplication. The resulted algebra is
provides a nice algebra, with the usual pointwise multiplication. The resulted algebra is 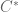 -algbra (in fact a von Neumann algebra). For
-algbra (in fact a von Neumann algebra). For 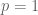 , we have a Banach algebra with convolution as multiplication. And for other
, we have a Banach algebra with convolution as multiplication. And for other  , there is no algebra.
, there is no algebra.
I have a question. Some of function space are known to be algrbras as well, some are not. For example, as it is well-known, in
It is interesting for me to have an interpretaion of this phenemenon, but I’m not able to do so
31 December, 2020 at 11:54 am
Terence Tao
Well, all the spaces for
spaces for 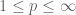 are Banach algebras with respect to pointwise multiplication; admittedly only the
are Banach algebras with respect to pointwise multiplication; admittedly only the  one is unital, but one could for instance adjoin a unit to create a unital Banach algebra
one is unital, but one could for instance adjoin a unit to create a unital Banach algebra  . So I don’t think there is any particularly simple relationship between the exponent of integrability of a space and its propensity to be a Banach algebra. (On the other hand,
. So I don’t think there is any particularly simple relationship between the exponent of integrability of a space and its propensity to be a Banach algebra. (On the other hand, 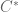 algebras are most naturally thought of as spaces with
algebras are most naturally thought of as spaces with 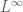 type norms (or operator norms, in the noncommutative case), as one sees from the Gelfand-Naimark theorem.)
type norms (or operator norms, in the noncommutative case), as one sees from the Gelfand-Naimark theorem.)
16 March, 2010 at 5:34 am
Andrew Bailey
Wow, really nice article. It’s given me a whole new perspective. Thanks. :-)
16 March, 2010 at 10:31 am
Anonymous
Dear Terry,
Dumb question: How is regularity defined on discrete spaces?
19 March, 2010 at 2:53 pm
Terence Tao
One can use discrete derivatives (i.e. divided differences) or the Fourier transform. In the discrete case, the Sobolev space hierarchy collapses (e.g.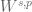 collapses to
collapses to 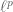 ), as the derivative operators are now bounded in
), as the derivative operators are now bounded in 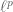 .
.
17 March, 2010 at 1:57 pm
timur
I have seen that some version of this diagram was called “the DeVore diagram”, in approximation theory talks or literature.
19 March, 2010 at 4:44 am
Ming Wang
What a nice diagram! How can I apply it to other function spaces, such as Morrey spaces and Campanato spaces?
22 March, 2010 at 10:42 pm
maxbaroi
I remember a crude pre-alpha-version of this diagram in 245C last semester. I’m glad you were able to finish it. It is extremely helpful.
27 March, 2010 at 6:15 am
Anonymous
Dear Terry,
Excellent post! If I may ask, what program did you use to draw the diagram?
27 March, 2010 at 8:37 am
Terence Tao
The diagram was initially drawn on Winfig.
2 April, 2010 at 10:02 pm
Amplitude-frequency dynamics for semilinear dispersive equations « What’s new
[…] sometimes acquires a reputation for being unduly technical as a consequence. However, as noted in a previous blog post, one can view function space norms as a way to formalise the intuitive notions of the […]
10 May, 2010 at 1:55 pm
Anonymous
Minor typo:
“The Sobolev spaces W^{s,p} of functions f of functions whose norm”
should be
“The Sobolev spaces W^{s,p} of functions f whose norm”
[Corrected, thanks – T.]
30 August, 2010 at 6:54 pm
A type diagram for function spaces (via What’s new) | Hello, world!
[…] In harmonic analysis and PDE, one often wants to place a function on some domain (let's take a Euclidean space for simplicity) in one or more function spaces in order to quantify its "size" in some sense. Examples include The Lebesgue spaces of functions whose norm is finite, as well as their relatives such as the weak $ … Read More […]
15 March, 2011 at 9:07 am
yucao
The picture is very nice. What kind of software did you use for the diagram?
15 March, 2011 at 9:56 am
Terence Tao
xfig (or more precisely, winfig).
16 July, 2011 at 7:53 pm
Nice picture « Hello, world!
[…] A type diagram for function space from Terence Tao: […]
11 September, 2015 at 11:36 am
Tati
Dear Professor Tao, is there any way to quantify how large or small e.g. the set of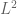 functions in the set of
functions in the set of  functions (defined on the same interval), or e.g. how small the set of differentiable functions in the set of all continuous functions (defined on the same interval).
functions (defined on the same interval), or e.g. how small the set of differentiable functions in the set of all continuous functions (defined on the same interval).
11 September, 2015 at 11:42 am
Terence Tao
The classical approach is through Baire Category; it is an instructive exercise to show for instance that![L^2([0,1])](https://s0.wp.com/latex.php?latex=L%5E2%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) is a meager subset of
is a meager subset of ![L^1([0,1])](https://s0.wp.com/latex.php?latex=L%5E1%28%5B0%2C1%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . Nowadays one also sees more quantitative ways to measure the smallness of a subset of a Banach space, e.g. covering numbers, Gelfand width, etc. One can also work in finite dimensions and ponder, for instance, the relative sizes of the unit octahedron in
. Nowadays one also sees more quantitative ways to measure the smallness of a subset of a Banach space, e.g. covering numbers, Gelfand width, etc. One can also work in finite dimensions and ponder, for instance, the relative sizes of the unit octahedron in 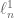 and the unit ball in
and the unit ball in  . The general area of high dimensional geometry addresses these sorts of questions, see e.g. Pisier’s book on the subject.
. The general area of high dimensional geometry addresses these sorts of questions, see e.g. Pisier’s book on the subject.
11 September, 2015 at 11:48 am
Tati
This is very helpful! Thanks so much!
6 November, 2015 at 6:28 pm
Anonymous
Let be an open set of
be an open set of  . I saw in Evan’s Partial Differential Equations
. I saw in Evan’s Partial Differential Equations
and
In Hunter’s Applied Analysis, consists of functions whose partial derivatives of order less than or equal to
consists of functions whose partial derivatives of order less than or equal to  are uniformly continuous in
are uniformly continuous in  .
.
Also, I’ve seen some people define as functions in
as functions in 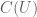 that can be extended as functions in
that can be extended as functions in  .
.
Leoni points out in his First Course in Sobolev Spaces that while the definitions of the spaces and $C^\infty(U)$ are standard, in the literature there are different definitions of the spaces
and $C^\infty(U)$ are standard, in the literature there are different definitions of the spaces  and
and  , and “unfortunately these definitions do not coincide”.
, and “unfortunately these definitions do not coincide”.
I’ve seen defined as in an undergraduate real analysis course that
defined as in an undergraduate real analysis course that
Would you clarify what is really going on with the spaces ? How do PDE people usually think about such issue when a general open domain is considered?
? How do PDE people usually think about such issue when a general open domain is considered?
[Sorry, I do not really understand the question here. As Leoni states, there is no consensus on the notation here: each paper or text simply uses the notations that are most convenient for the application at hand, and one has to read the notational conventions carefully in those cases. It’s also worth bearing in mind that notation is ultimately an artificial human invention, rather than an innate feature of the mathematics one is working on; sometimes, two writers happen to use the same symbol to denote two rather different concepts, but this does not necessarily mean that these concepts have any deeper connection to them. -T.]
7 November, 2015 at 7:17 am
Anonymous
Ah, sorry for the confusion. What really puzzles me is the definitions of ,
,  and
and  for general open subset
for general open subset  in
in  . (The classical regularity spaces
. (The classical regularity spaces 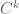 , as you put it in this post.)
, as you put it in this post.)
In Evan’s book,
where
In Hunter’s Applied Analysis, consists of functions that are uniformly continuous in
consists of functions that are uniformly continuous in  .
.
ect. (At least four different definitions appear as I asked in the previous question.)
My question is, do definitions of (
(  ,
,  ) completely depend on context (so that there is no “the” definition)? Do they have any “stronger”, “weaker” relationship to each other or are these definitions not comparable at all?
) completely depend on context (so that there is no “the” definition)? Do they have any “stronger”, “weaker” relationship to each other or are these definitions not comparable at all?
7 November, 2015 at 7:25 am
Terence Tao
In all of these cases, is a subspace of
is a subspace of 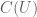 consisting of functions that somehow have “good behaviour at the boundary”, but the precise nature of “good behaviour” is different in different texts. There are some obvious inclusions between the different versions of
consisting of functions that somehow have “good behaviour at the boundary”, but the precise nature of “good behaviour” is different in different texts. There are some obvious inclusions between the different versions of  (e.g. if one is uniformly continuous, one is certainly also uniformly continuous on bounded subsets) but most likely the spaces are otherwise distinct from each other. Similarly for
(e.g. if one is uniformly continuous, one is certainly also uniformly continuous on bounded subsets) but most likely the spaces are otherwise distinct from each other. Similarly for  and
and  .
.
26 September, 2016 at 5:40 am
Anonymous
A recent question with an accepted answer on MO (http://mathoverflow.net/q/250444/14319) might be related to this discussion.
25 October, 2018 at 2:12 am
FUA Kap01-AB04 Klassische Banachräume | UGroh's Weblog
[…] Viele weitere Beispiele findet man in [Dunford–Schwartz](Chapter IV) und in der Übersicht von T. Tao: A Type Diagram for Function Spaces. […]
12 November, 2020 at 12:12 pm
Mary
I strongly agree in this point:
____
there is an entire “zoo of function spaces” one could consider, and it can be difficult at first to see how they are organised with respect to each other.
2 February, 2021 at 8:30 am
Uncertainty principle, Sobolev embedding, and norm estimates ~ MathOverflow ~ mathubs.com
[…] Tao offers a nice discussion of different function spaces in this blog. In the blog there is an explanation of the tradeoff between regularity $s$ and integrability $p$, […]
14 February, 2023 at 7:13 am
Anonymous
Can one add the space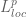 somewhere in the diagram?
somewhere in the diagram?