In most undergraduate courses, groups are first introduced as a primarily algebraic concept – a set equipped with a number of algebraic operations (group multiplication, multiplicative inverse, and multiplicative identity) and obeying a number of rules of algebra (most notably the associative law). It is only somewhat later that one learns that groups are not solely an algebraic object, but can also be equipped with the structure of a manifold (giving rise to Lie groups) or a topological space (giving rise to topological groups). (See also this post for a number of other ways to think about groups.)
Another important way to enrich the structure of a group is to give it some geometry. A fundamental way to provide such a geometric structure is to specify a list of generators
of the group
. Let us call such a pair
a generated group; in many important cases the set of generators
is finite, leading to a finitely generated group. A generated group
gives rise to the word metric
on
, defined to be the maximal metric for which
for all
and
(or more explicitly,
is the least
for which
for some
and
). This metric then generates the balls
. In the finitely generated case, the
are finite sets, and the rate at which the cardinality of these sets grow in
is an important topic in the field of geometric group theory. The idea of studying a finitely generated group via the geometry of its metric goes back at least to the work of Dehn.
One way to visualise the geometry of a generated group is to look at the (labeled) Cayley colour graph of the generated group . This is a directed coloured graph, with edges coloured by the elements of
, and vertices labeled by elements of
, with a directed edge of colour
from
to
for each
and
. The word metric then corresponds to the graph metric of the Cayley graph.
For instance, the Cayley graph of the cyclic group with a single generator
(which we draw in green) is given as
while the Cayley graph of the same group but with the generators (which we draw in blue and red respectively) is given as
We can thus see that the same group can have somewhat different geometry if one changes the set of generators. For instance, in a large cyclic group , with a single generator
the Cayley graph “looks one-dimensional”, and balls
grow linearly in
until they saturate the entire group, whereas with two generators
chosen at random, the Cayley graph “looks two-dimensional”, and the balls
typically grow quadratically until they saturate the entire group.
Cayley graphs have three distinguishing properties:
- (Regularity) For each colour
, every vertex
has a single
-edge leading out of
, and a single
-edge leading into
.
- (Connectedness) The graph is connected.
- (Homogeneity) For every pair of vertices
, there is a unique coloured graph isomorphism that maps
to
.
It is easy to verify that a directed coloured graph is a Cayley graph (up to relabeling) if and only if it obeys the above three properties. Indeed, given a graph with the above properties, one sets
to equal the (coloured) automorphism group of the graph
; arbitrarily designating one of the vertices of
to be the identity element
, we can then identify all the other vertices in
with a group element. One then identifies each colour
with the vertex that one reaches from
by an
-coloured edge. Conversely, every Cayley graph of a generated group
is clearly regular, is connected because
generates
, and has isomorphisms given by right multiplication
for all
. (The regularity and connectedness properties already ensure the uniqueness component of the homogeneity property.)
From the above equivalence, we see that we do not really need the vertex labels on the Cayley graph in order to describe a generated group, and so we will now drop these labels and work solely with unlabeled Cayley graphs, in which the vertex set is not already identified with the group. As we saw above, one just needs to designate a marked vertex of the graph as the “identity” or “origin” in order to turn an unlabeled Cayley graph into a labeled Cayley graph; but from homogeneity we see that all vertices of an unlabeled Cayley graph “look the same” and there is no canonical preference for choosing one vertex as the identity over another. I prefer here to keep the graphs unlabeled to emphasise the homogeneous nature of the graph.
It is instructive to revisit the basic concepts of group theory using the language of (unlabeled) Cayley graphs, and to see how geometric many of these concepts are. In order to facilitate the drawing of pictures, I work here only with small finite groups (or Cayley graphs), but the discussion certainly is applicable to large or infinite groups (or Cayley graphs) also.
For instance, in this setting, the concept of abelianness is analogous to that of a flat (zero-curvature) geometry: given any two colours , a directed path with colours
(adopting the obvious convention that the reversal of an
-coloured directed edge is considered an
-coloured directed edge) returns to where it started. (Note that a generated group
is abelian if and only if the generators in
pairwise commute with each other.) Thus, for instance, the two depictions of
above are abelian, whereas the group
, which is also the dihedral group of the triangle and thus admits the Cayley graph
is not abelian.
A subgroup of a generated group
can be easily described in Cayley graph language if the generators
of
happen to be a subset of the generators
of
. In that case, if one begins with the Cayley graph of
and erases all colours except for those colours in
, then the graph foliates into connected components, each of which is isomorphic to the Cayley graph of
. For instance, in the above Cayley graph depiction of
, erasing the blue colour leads to three copies of the red Cayley graph (which has
as its structure group), while erasing the red colour leads to two copies of the blue Cayley graph (which as
as its structure group). If
is not contained in
, then one has to first “change basis” and add or remove some coloured edges to the original Cayley graph before one can obtain this formulation (thus for instance
contains two more subgroups of order two that are not immediately apparent with this choice of generators). Nevertheless the geometric intuition that subgroups are analogous to foliations is still quite a good one.
We saw that a subgroup of a generated group
with
foliates the larger Cayley graph into
-connected components, each of which is a copy of the smaller Cayley graph. The remaining colours in
then join those
-components to each other. In some cases, each colour
will connect a
-component to exactly one other
-component; this is the case for instance when one splits
into two blue components. In other cases, a colour
can connect a
-component to multiple
-components; this is the case for instance when one splits
into three red components. The former case occurs precisely when the subgroup
is normal. (Note that a subgroup
of a generated group
is normal if and only if left-multiplication by a generator of
maps right-cosets of
to right-cosets of
.) We can then quotient out the
Cayley graph from
, leading to a quotient Cayley graph
whose vertices are the
-connected components of
, and the edges are projected from
in the obvious manner. We can then view the original graph
as a bundle of
-graphs over a base
-graph (or equivalently, an extension of the base graph
by the fibre graph
); for instance
can be viewed as a bundle of the blue graph
over the red graph
, but not conversely. We thus see that the geometric analogue of the concept of a normal subgroup is that of a bundle. The generators in
can be viewed as describing a connection on that bundle.
Note, though, that the structure group of this connection is not simply , unless
is a central subgroup; instead, it is the larger group
, the semi-direct product of
with its automorphism group. This is because a non-central subgroup
can be “twisted around” by operations such as conjugation
by a generator
. So central subgroups are analogous to the geometric notion of a principal bundle. For instance, here is the Heisenberg group
over the field of two elements, which one can view as a central extension of
(the blue and green edges, after quotienting) by
(the red edges):
Note how close this group is to being abelian; more generally, one can think of nilpotent groups as being a slight perturbation of abelian groups.
In the case of (viewed as a bundle of the blue graph
over the red graph
), the base graph
is in fact embedded (three times) into the large graph
. More generally, the base graph
can be lifted back into the extension
if and only if the short exact sequence
splits, in which case
becomes a semidirect product
of
and a lifted copy
of
. Not all bundles can be split in this fashion. For instance, consider the group
, with the blue generator
and the red generator
:
This is a -bundle over
that does not split; the blue Cayley graph of
is not visible in the
graph directly, but only after one quotients out the red fibre subgraph. The notion of a splitting in group theory is analogous to the geometric notion of a global gauge. The existence of such a splitting or gauge, and the relationship between two such splittings or gauges, are controlled by the group cohomology of the sequence
.
Even when one has a splitting, the bundle need not be completely trivial, because the bundle is not principal, and the connection can still twist the fibres around. For instance, when viewed as a bundle over
with fibres
splits, but observe that if one uses the red generator of this splitting to move from one copy of the blue
graph to the other, that the orientation of the graph changes. The bundle is trivialisable if and only if
is a direct summand of
, i.e.
splits as a direct product
of a lifted copy
of
. Thus we see that the geometric analogue of a direct summand is that of a trivialisable bundle (and that trivial bundles are then the analogue of direct products). Note that there can be more than one way to trivialise a bundle. For instance, with the Klein four-group
,
the red fibre is a direct summand, but one can use either the blue lift of
or the green lift of
as the complementary factor.







44 comments
Comments feed for this article
10 July, 2010 at 4:27 pm
Andrew L.
First off, I LOVE these “by the way” lecture posts of yours,Professor Tao. They’re a great resource for the entire mathematical community. It’s very comforting to know there’s a top notch researcher who seems just as passionate about teaching as you are. Keep up the great work.
The serious study of the geometric properties of groups and thier associated graph embeddings in Euclidean spaces-which was initiated by Klein and developed by so many great mathematicians,most notably Wilhelm Magnus and his students-is a fantasticaly rich topic that isn’t incorporated into traditional courses in algebra and geometry anywhere near as fully as it should be. The classic introduction is of course, GRAPHS AND THIER GROUPS by Grossman and Magnus. A much more advanced text that covers the graph theoretic aspects-including the deeper topological properties of the Cayley graph and it’s fundamental group structure touched on in your post-can be found in GRAPHS OF GROUPS ON SURFACES by Arthur T.White,currently in it’s 3rd edition.
Again,thanks for the great introduction to such an important topic.
10 July, 2010 at 5:26 pm
Theo
It’s a well-known fact that a connected topological group is generated by any open neighborhood of its identity element. (So it is tempting to think of a Lie group as _generated_ by its Lie algebra, after identifying the Lie algebra with an infinitesimal neighborhood of the identity. This is reasonable in models of mathematics where infinite numbers really exist. Moreover, the Baker-Campbell-Hausdorff series identifies the Lie algebra with the formal group, and over the BCH series converges for finite-dimensional Lie algebras in a non-trivial neighborhood of the origin, and so you really can identity a neighborhood of the Lie algebra with a neighborhood of the Lie group.) So it is tempting to take some sort of “formal neighborhood” of the identity element as my generating set
the BCH series converges for finite-dimensional Lie algebras in a non-trivial neighborhood of the origin, and so you really can identity a neighborhood of the Lie algebra with a neighborhood of the Lie group.) So it is tempting to take some sort of “formal neighborhood” of the identity element as my generating set  . Can I then think of the topology on $G$ as coming from some sort of “formal Cayley graph”? Maybe I will ask this over on MathOverflow.
. Can I then think of the topology on $G$ as coming from some sort of “formal Cayley graph”? Maybe I will ask this over on MathOverflow.
10 July, 2010 at 9:04 pm
Terence Tao
Yes, one can view topological groups and Lie groups as being continuous analogues of generated groups, and indeed a significant portion of geometric group theory is devoted to viewing the former as asymptotic limits of the latter (e.g. Gromov’s original proof of Gromov’s theorem on groups of polynomial growth definitely falls into this category). The literature on Hilbert’s fifth problem (which, roughly speaking, asks whether all locally compact topological groups come from Lie groups) don’t explicitly use Cayley graphs, but it seems to be lurking beneath the surface (particularly with those solutions to that problem that use nonstandard analysis).
10 July, 2010 at 7:52 pm
Jair
Fascinating stuff. I didn’t realize that groups were so closely connected with certain graphs. Thanks for posting this.
10 July, 2010 at 9:36 pm
alex
I like the commonsense explanation of normal groups that comes out of this presentation. By contrast, the usual definition ( g n g^{-1} \in G) is unintuitive despite its simplicity.
11 July, 2010 at 5:04 am
John Armstrong
So a Cayley graph is not associated with a group, but with a presented group. It’d be nice to have something that only depended on the group itself, and not the presentation. (And yes, I do know where this goes…)
12 July, 2010 at 7:48 am
Terence Tao
To be utterly pedantic, a presented group is a slightly richer object than a generated group (which, in turn, is richer than a raw group); a presented group is a group with a distinguished set of generating elements and a distinguished set of generating relations, whereas a generated group only has the former and not the latter. (So there are forgetful functors from the category of presented groups to the category of generated groups to the category of groups.) Cayley graphs are more naturally associated with generated groups than with presented groups.
In the case of infinite finitely generated groups, changing the choice of generators only affects the word metric by a bilipschitz distortion. As such, the asymptotic (coarse) geometry of the finitely generated group does not depend on the choice of generators (e.g. the concept of a finitely generated group of polynomial growth does not depend on the choice of generators). Much of geometric group theory focuses on this asymptotic geometry and so indeed one can focus primarily on groups themselves rather than on generated groups. However, if one wants to work more quantitatively and non-asymptotically (and specifically, if one wants to talk about results that are non-trivial even for finite groups) then the choice of generators becomes more important. For instance, as discussed above, a cyclic group can look one-dimensional, two-dimensional, or many-dimensional at various scales, depending on how many generators one selects and how commensurate they are to each other.
15 December, 2019 at 5:02 pm
Anonymous
quasi-isometry/ the geometry of the group.
not dependent on the choice of generators/ the presentation.
11 July, 2010 at 10:00 am
Anonymous
typo in the second paragraph: $y = s_1^{\epsilon_1} \ldots s_m^{\epsilon_m} y$ should be $y = s_1^{\epsilon_1} \ldots s_m^{\epsilon_m} x$. Thanks for the post.
[Corrected, thanks – T.]
12 July, 2010 at 1:35 pm
Anonymous
Could you elaborate on the third property (Homogeneity) of the Cayley Graph?
Is this saying that there aren’t two paths between x and y of the same color and direction along each step?
Thanks.
15 July, 2010 at 9:08 am
Terence Tao
No, this is already a consequence of the regularity hypothesis.
One way to view homogeneity is that it asserts that any graph theoretic statement that is true if one uses x as a starting vertex, is also true if one uses y as a starting vertex, so that all vertices “look the same” from a graph theoretic perspective. For instance, in the Z/9Z graph, no matter where one starts from, the operation of following three blue arrows is always equal to following one red arrow. If three blues equaled a red for one starting vertex x but not for another y, then the graph would not be homogeneous.
The formal definition of homogeneity requires the notion of a graph isomorphism,
http://en.wikipedia.org/wiki/Graph_isomorphism
12 July, 2010 at 10:47 pm
Artem
«Latex path not specified» in place of several formulas. About eight hours ago everything was OK.
Thanks for interesting post!
15 July, 2010 at 9:30 am
Anonymous
I am pleased by this post, and I would like to understand better why the group properties discussed here are geometric?
Is it because they are (geo)metric? But it’s a word metric, why isn’t it algebraic?
The notion of ‘ball’ is not geometric either. Is ‘(polynomial) growth’ a geometric concept? you just count how many words there are of length 1,2,3,.. in your generated group.
That a group is abelian is visible from a multiplication table (anyway visualisation of Cayley graphs is restricted to ‘small’ groups).
“Nevertheless the geometric intuition that subgroups are analogous to foliations is still quite a good one.”
It would be interesting to know how it could help. Why is it really geometric? The notion of ‘metric’ is not engaged here. Is it geometric because it is visualised and explained by means of symbolism embedded in Euclidean plain? Yes, this method is used in geometry, but not only in geometry, in analysis, for example, too.
The fact that “one can view topological groups and Lie groups as being continuous analogues of generated groups” gives another view on group but does not add geometric properties, it seems to me. please, tell me if I am wrong.
15 July, 2010 at 10:04 am
Terence Tao
Groups are both algebraic objects and geometric objects; it is not a dichotomy.
While metric geometry is certainly an important component of modern geometry, metrics are certainly not the only geometric objects of study. Riemannian geometry, for instance, is definitely very much concerned with volumes of balls, among other things. Differential geometry and its relatives (e.g. contact geometry) is similarly quite concerned with foliations, bundles, and connections. Kleinian geometry focuses on the notion of symmetry, which is very much a group-theoretic concept also. (The classical Euclidean geometry of points, lines, and planes can be viewed as a special case of all of the above modern types of geometry.)
Traditionally, geometry has focused mostly on continuous structures, but nowadays discrete geometries are also an important area of study, and Cayley graphs form a basic example of such.
16 July, 2010 at 6:23 am
Anonymous
Is it not a dichotomy in the sense that groups have algebraic and geometric properties or in the sense, the same properties of groups can be seen as algebraic and as geometric properties? or are there properties of groups which are certainly geometric but not algebraic? Because what is ‘geometric’ at the first glance, seems to be perfectly algebraic: e.g. metric, hyperbolicity can be formulated algebraically, Cayley graphs -aren’t they algebraic objects?
16 July, 2010 at 1:58 pm
Terence Tao
Almost every fundamental concept or object in mathematics can be interpreted in a number of different ways (algebraic, geometric, dynamical, analytical, etc.), and it is important to internalise as many of these as one can in order to truly understand these concepts. I recommend the discussion in Thurston’s article “On proof and progress in mathematics” for further reading. (Section 2 is the most relevant here, but the entire article is worthwhile.)
15 July, 2010 at 11:16 am
Anonymous
Naive question: How do you yourself distinguish algebraic objects from geometric objects? I didn’t find the relevant wikipedia article especially helpful in this regard.
15 July, 2010 at 7:09 pm
xiaodong xu
Dear Terry, you wrote
•(Connectedness) The graph is connected.
This may not be true for some Cayley graphs. For instance, Z/8Z and S={2}.
Yes?
16 July, 2010 at 8:09 am
Terence Tao
{2} does not generate Z/8Z.
16 July, 2010 at 3:49 am
westy31
Dear Terrence,
I thought it would be interesting to mention the relationship between Cayley graphs and tilings. I have some pictures on thi on my web page:
http://www.xs4all.nl/~westy31/Geometry/Geometry.html#Cayley
Basically, you can take any Cayley graph with 2 generators, and turn it into a tiling of a Riemann surface. Each tile corresponds to a vertex of the Cayley graph. Since any finite simple group can be generated by 2 generators, all finite simple groups are a tiling of a Riemann surface. Also, you can interpret the tiling itself as a Cayly graph, by labeling rotations around the vertices as generators.
One question that comes to mind if the genus of the surface has some group theoretic meaning.
Gerard
18 July, 2010 at 7:22 am
Jason Rute
Interesting article. In the second paragraph after the picture of S_3 you mention it can be split into “two red components” and “three blue components”. I believe you mean “two blue components” and “three red components”.
[Corrected, thanks – T.]
19 July, 2010 at 1:21 am
student
You wrote:
“In some cases, each colour {s \in S\backslash S’} will connect a {S’}-component to exactly one other {S’}-component; this is the case for instance when one splits {S_3} into three red components. In other cases, a colour {s} can connect a {S’}-component to multiple {S’}-components; this is the case for instance when one splits {S_3} into two blue components. ”
which should probably (???) read:
In some cases, each colour {s \in S\backslash S’} will connect a {S’}-component to exactly one other {S’}-component; this is the case for instance when one splits {S_3} into two blue components. In other cases, a colour {s} can connect a {S’}-component to multiple {S’}-components; this is the case for instance when one splits {S_3} into three red components.
[Oops! I implemented a previous fix incorrectly. Thanks, it should be correct now – T.]
25 July, 2010 at 5:40 am
Politopos. « US Patent Appl. 12213303: Comentarios.
[…] 3….y un post muy informativo sobre grafos de Cayley como “representación geometrica” de grupos: https://terrytao.wordpress.com/2010/07/10/cayley-graphs-and-the-geometry-of-groups/ […]
27 August, 2010 at 1:46 am
marry
Hi,
I am newly interested in cayley graph. I read note on cayley graphs. may be it is very clear but I could not understand how can I draw ,i.e. how can ı draw directed edge? you gave example for 6Z and S={1}. as you say, I use from x to sx. but only one element exists in S and then edge is from 1 to 1, 2 to 2… and so on. Can I misunderstand?
27 August, 2010 at 9:06 am
Terence Tao
In the case of an additive group such as rather than a multiplicative group
rather than a multiplicative group 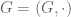 , one would connect x to s+x, rather than x to sx.
, one would connect x to s+x, rather than x to sx.
29 August, 2010 at 1:08 am
marry
Dear Prof. Tao,
firstly, thanks for answering my previous question.
I wonder that all inverse element of S is also S. Is this necessary or not?
in your note about cayley graphs you did not wrote but some books add this condition.
and you said that word metric is the maximal metric .What reason is maximal?
best regards,
30 August, 2010 at 8:46 am
Terence Tao
There are two types of Cayley graphs: directed Cayley graphs (the ones discussed here) and undirected Cayley graphs. The latter require a symmetric set of generators, and the former does not.
The word metric is maximal with respect to the pointwise order on metrics (in which one writes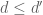 for two metrics d,d’ if one has
for two metrics d,d’ if one has 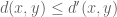 for all x,y) subject to the constraint that
for all x,y) subject to the constraint that  for all x in G and s in S. This is a succinct way to define the word metric, but perhaps not the most enlightening, which is why I also added a more explicit description of that metric.
for all x in G and s in S. This is a succinct way to define the word metric, but perhaps not the most enlightening, which is why I also added a more explicit description of that metric.
18 May, 2012 at 9:54 pm
Son
Dear prof. Tao,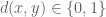 only? Only that would make sense to me because this is kind of defining a metric of orbit of
only? Only that would make sense to me because this is kind of defining a metric of orbit of  . What we care here is to establish the connection between
. What we care here is to establish the connection between  and its orbits. If the action of
and its orbits. If the action of 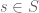 on
on  results in
results in  ,
, 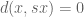 . Otherwise, it is
. Otherwise, it is 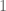 .
.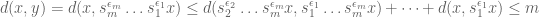 .
.
Would
If that’s the case,
That’s how I can make sense of this. Please correct me if I’m wrong.
31 August, 2010 at 3:21 am
marry
Dear prof. Tao,
you said that a directed coloured graph is a Cayley graph (up to relabeling) if and only if it obeys the above three properties. I understand one way of the proof. conversely for showing that cayley graph satisfy property of Homogeneity ,you use right multiplication xg. Can we choose left multiplication instead of right?
best regards,
27 August, 2011 at 11:35 am
254A, Notes 0 – Hilbert’s fifth problem and related topics « What’s new
[…] describes the geometry of the Cayley graph on formed by connecting to for each and . (See this previous post for more discussion of using Cayley graphs to study groups […]
11 May, 2012 at 10:51 am
Cayley graphs and the algebra of groups « What’s new
[…] is a sequel to my previous blog post “Cayley graphs and the geometry of groups“. In that post, the concept of a Cayley graph of a group was used to place some geometry on […]
18 November, 2013 at 9:49 pm
geometric conceptions of groups (and walks of graphs from groups); Heisenburg group | Peter's ruminations
[…] https://terrytao.wordpress.com/2010/07/10/cayley-graphs-and-the-geometry-of-groups/ […]
3 February, 2014 at 3:58 am
Imran
I want to ask a question…that If we have a finite presentation of a group, but order of the generators are unknown, then can we draw a cayley graph of that group?? if yes, then by which mean
3 August, 2014 at 7:01 am
Tuấn Bùi
Reblogged this on Tuấn Bùi and commented:
Archived!
14 October, 2014 at 7:15 pm
Anonymous
Does the undirected cayley graph representation of a group always have a hamiltonian cycle for any choice of generators?
15 October, 2014 at 7:02 am
Terence Tao
This turns out to be a well studied problem with many partial results, though still far from completely solved: http://www.sciencedirect.com/science/article/pii/0012365X95000725
20 February, 2015 at 3:20 am
Groups and Group Actions: Lecture 2 | Theorem of the week
[…] in various places, for example Fields medallist Terry Tao has written about them on his blog, e.g. here (warning: this post assumes knowledge of more advanced maths than first-year undergraduates usually […]
21 February, 2015 at 2:58 am
Anonymous
Another interesting example is the study of the subgroup of algebraic functions (of one complex variable over the Riemann sphere) generated by compositions of (all branches) of finitely many algebraic functions.
4 May, 2015 at 7:25 am
Valentino
I have a (probably) easy question.
Given a generating set S for a group G, I ask if the following proposition is true or not: “G has exactly one longest element wrt S if and only if S is a minimal generating set” ???
I know that this question can also be interpreted in terms of “minimal” Cayley graphs, but I can’t realize if it’s true or not.
21 September, 2015 at 3:26 am
tomcircle
Reblogged this on Math Online Tom Circle and commented:
Terence Tao’s wrote this easy-to-understand Group Theory. It is rare for mathematicians to be also a good writer in explaining difficult math in layman’s terms. Highly recommended!
20 February, 2016 at 7:53 am
peterisdaugulis
Dear Terrence,
have induced cycles (cycles without chords) of Cayley graphs been studied as essential relations for the given generators? Are there any references?
15 January, 2017 at 1:08 pm
Groups and graphs (and computation) | Bahçemizi Yetiştermeliyiz
[…] a group G, or more specifically a finite set S of generators for G, one can form the Cayley graph by taking the vertex set to be the set of group elements, and adding an edge iff for some […]
22 February, 2017 at 3:08 am
Groups and Group Actions: Lecture 2 | Theorem of the week
[…] in various places, for example Fields medallist Terry Tao has written about them on his blog, eg here (warning: this post assumes knowledge of more advanced maths than first-year undergraduates usually […]
16 November, 2017 at 6:15 pm
Graph operators on Discrete Groups – oolongteafan1
[…] https://terrytao.wordpress.com/2010/07/10/cayley-graphs-and-the-geometry-of-groups/ […]