The main purpose of this post is to roll over the discussion from the previous Polymath8 thread, which has become rather full with comments. As with the previous thread, the main focus on the comments to this thread are concerned with writing up the results of the Polymath8 “bounded gaps between primes” project; the latest files on this writeup may be found at this directory, with the most recently compiled PDF file (clocking in at about 90 pages so far, with a few sections still to be written!) being found here. There is also still some active discussion on improving the numerical results, with a particular focus on improving the sieving step that converts distribution estimates such as into weak prime tuples results
. (For a discussion of the terminology, and for a general overview of the proof strategy, see this previous progress report on the Polymath8 project.) This post can also contain any other discussion pertinent to any aspect of the polymath8 project, of course.
There are a few sections that still need to be written for the draft, mostly concerned with the Type I, Type II, and Type III estimates. However, the proofs of these estimates exist already on this blog, so I hope to transcribe them to the paper fairly shortly (say by the end of this week). Barring any unexpected surprises, or major reorganisation of the paper, it seems that the main remaining task in the writing process would be the proofreading and polishing, and turning from the technical mathematical details to expository issues. As always, feedback from casual participants, as well as those who have been closely involved with the project, would be very valuable in this regard. (One small comment, by the way, regarding corrections: as the draft keeps changing with time, referring to a specific line of the paper using page numbers and line numbers can become inaccurate, so if one could try to use section numbers, theorem numbers, or equation numbers as reference instead (e.g. “the third line after (5.35)” instead of “the twelfth line of page 54”) that would make it easier to track down specific portions of the paper.)
Also, we have set up a wiki page for listing the participants of the polymath8 project, their contact information, and grant information (if applicable). We have two lists of participants; one for those who have been making significant contributions to the project (comparable to that of a co-author of a traditional mathematical research paper), and another list for those who have made auxiliary contributions (e.g. typos, stylistic suggestions, or supplying references) that would typically merit inclusion in the Acknowledgments section of a traditional paper. It’s difficult to exactly draw the line between the two types of contributions, but we have relied in the past on self-reporting, which has worked pretty well so far. (By the time this project concludes, I may go through the comments to previous posts and see if any further names should be added to these lists that have not already been self-reported.)

132 comments
Comments feed for this article
14 September, 2013 at 10:23 am
Aubrey de Grey
There may be a case for closing (or highlighting, if it can’t be easily closed) one further ostensible open door, relating to Remark 7.10. That Remark arises from Terry’s post https://terrytao.wordpress.com/2013/09/02/polymath8-writing-the-paper-ii/#comment-243825 in which he established, after more detailed inspection, that the initially promising-looking use of Type II methods to establish a Type I constraint that works for some positive varpi unfortunately requires either a value of sigma too low to avoid the Type III case or else a Type II “level” (namely 4) that makes the overall complexity of the proof comparable to that of the Deligne-free Type I argument. However, what is not clear at first sight is whether elevation of the Type II arguments all the way through the unexplored levels 4, 5 and 6 has any chance of translating into Type I numerology that improves on the current best Type I constraint. It might be worth mentioning something about this option: if it can be easily disposed of by means that I have overlooked then maybe a sentence in Remark 7.10 would suffice, but otherwise it arguably merits a new paragraph in Section 11.
14 September, 2013 at 12:31 pm
Aubrey de Grey
Quick addendum: I guess that, for completeness, any such comment might best also note (if only to dismiss) the possibility that the repurposing of Type II methods to the Type I setting could be performed by more elaborate but numerically superior (in terms of the varpi thereby obtained) means than the replacement specified at the beginning of Remark 7.10.
15 September, 2013 at 12:28 pm
pigh3
Line 2 of Sec 4.5 should refer to Section 4.4, not 4.5.
[Corrected, thanks – T.]
15 September, 2013 at 6:05 pm
pigh3
1. 2nd display above (5.8), under the summation symbol, should be
should be 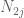 .
.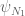 should be
should be 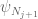 ?
?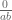 should be
should be 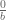 ?
?
2. Next display, in the middle of convolution,
3. 6 lines above Sec 6.1,
[Corrected, thanks – T.]
16 September, 2013 at 1:20 pm
RO'D
Katz’s name appears weirdly in [44] in the bibliography
[Corrected, thanks – T.]
16 September, 2013 at 6:38 pm
pigh3
1 line above (and also 5 lines below) (6.8), is it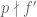 ?
?
[Fixed, thanks – T.]
17 September, 2013 at 5:53 pm
Eytan Paldi
The exact expression for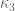 has a probabilistic interpretation from which I found a new upper bound for
has a probabilistic interpretation from which I found a new upper bound for 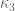 . I’m checking now the implication of this bound on
. I’m checking now the implication of this bound on 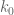 . I’ll send tomorrow the derivation of the new bounds for
. I’ll send tomorrow the derivation of the new bounds for 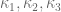 .
.
17 September, 2013 at 6:14 pm
pigh3
(6.15) through (6.16), all the should perhaps be
should perhaps be  ? (not the final
? (not the final  )
)
Right underneath, the interval should be (q/2, q/2].
[Corrected, thanks – T.]
18 September, 2013 at 11:34 am
Terence Tao
While working on the Deligne section of the paper, I discovered that it is possible to avoid explicitly using the deep theorem of Deligne, Laumon, and Katz which roughly speaking asserts that the Fourier transform of an admissible (Fourier) sheaf is again an admissible sheaf, with bounds on the conductor. To recall, the only place where we use this fact (other than in taking as a black box the existence of hyper-Kloosterman sheaves) is to establish square root cancellation for the sums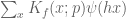 and
and 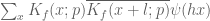 where
where
To do this we observed that the Fourier transform of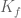 was basically
was basically 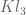 pulled back by a quadratic function, and then used Deligne-Laumon-Katz to write
pulled back by a quadratic function, and then used Deligne-Laumon-Katz to write 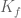 as the trace weight for an admissible sheaf with bounded conductor.
as the trace weight for an admissible sheaf with bounded conductor.
But if we take the Fourier transform first, we observe that the desired square root cancellation is equivalent to square root cancellation for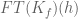 and
and 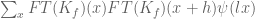 . So actually we don’t need
. So actually we don’t need 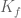 to be a good trace weight, it’s enough for
to be a good trace weight, it’s enough for 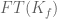 to be a good trace weight. Basically, we only need to perform Fourier transforms on the analytic side, not on the sheaf-theoretic side.
to be a good trace weight. Basically, we only need to perform Fourier transforms on the analytic side, not on the sheaf-theoretic side.
The way the paper is currently structured, though, it’s a bit tricky to take advantage of this simplification (and the simplification is modest from a length perspective, one can basically delete Section 8.6 and rewrite some subsequent theorems and proofs a little bit). Perhaps it is better to leave the structure of the paper as is but add a remark that one can avoid Deligne-Laumon-Katz if one really wanted to (but one still needs to construct the hyper-Kloosterman sheaf Kl_3, so one can’t escape DLK-type machinery completely).
18 September, 2013 at 12:59 pm
Philippe Michel
That is absolutely true ! and in fact I have written a first more elementary version of the proof as you suggest using Parseval to make the computation on the dual Fourier side (one can probably see this from digging through the older versions of deligne.tex in the dropbox folder; I will look to exhume it tomorrow); however I have chosen over the week-end to go for the stronger version -that the function itself is a trace function rather than only its fourier transform- after Friday discussions with Paul: indeed one could try to look for further improvement by exploiting averaging over some other parameters ($l$ for instance which for some configurations could be long enough wrt the factorization of $u$ – in place to do the vdc-method on the d variable- to perform a Polya-vinogradov completion on the other).
This explain also why the new proof is a bit less soft as its make explicit the dependency in the additional parameters of $f(x,y)$ ($a,b,c,d,e$) which are potentially going to vary. It is not clear whether this will work or whether this would be really worth the effort but at least part of the necessary material will be in place if necessary (and more importantly this is geometrically fun !). I think it is also good to keep with the stronger version because there might be other manipulations which do not rely on correlation of two functions ( admissible to Fourier analysis or iteration thereof) but on multiple -say quadruple type- correlation for which I don’t see how the Parseval could be applied (see the second Fouvry-Iwaniec paper in the list of references for an example).
And as you say we are already using serious stuff anyway. Another thing is that now the vdC method has been fully axiomatized to general statement (Prop 8.19 in which the initial datum are the trace functions and their sheaves) which could used by other for other problems
18 September, 2013 at 2:29 pm
Terence Tao
Yes, I agree that the current setup (based on the sheaf interpretation of the function itself rather than the Fourier transform) is more conceptually natural and better suited for future improvements; I’ve added a remark about the alternate route at Remark 8.19 and made some other small tweaks (e.g. taking advantage of symmetries to reduce the amount of calculation needed to compute the Fourier transform of K_f) but kept the overall structure unchanged.
20 September, 2013 at 11:46 am
Emmanuel Kowalski
Another reason to keep the Fourier transform is that, in fact, the existence / admissibility / conductor bound for the Fourier transform at the level we need can be done using arguments which are really quite a bit easier than the Riemann Hypothesis, as done in Section 8 of our preprint on conductor bounds
Click to access transforms.pdf
I think that the only thing needed in Polymath8 that this write-up does not explicitly state is the stability of (geometric) irreducibility, but this can be checked by the Plancherel formula and the “diophantine criterion for irreducibility” of Katz which we already state anyway (Lemma 5.10 in the paper; this depends on the Riemann Hypothesis). I’ll add this as an extra remark.
This does not give the full local analysis of singularities of the Fourier transform, but for most analytic applications, it will certainly be sufficient.
20 September, 2013 at 5:49 pm
pigh3
small typo: in 6th display of sec 9, “K;” should be “Kl”.
[Corrected, thanks – T.]
22 September, 2013 at 5:32 pm
Polymath8: Writing the paper, III | What's new
[…] main purpose of this post is to roll over the discussion from the previous Polymath8 thread, which has become rather full with comments. We are still writing the paper, but it appears to […]
22 September, 2013 at 5:34 pm
Terence Tao
I’m doing the usual rollover to refresh the thread; any comments on the polymath project that are not direct responses to comments already here should be made at the new thread.
28 September, 2013 at 4:56 am
Check in with Yitang Zhang « Pink Iguana
[…] Polymath8: Writing the paper, II, here. III, here. The paper is quite large now (164 pages!) but it is fortunately rather modular, and […]
15 November, 2018 at 4:12 pm
Ella Berum
Polymath8: Writing the paper, II | What
[…]The church today doesn’t need more programs
7 January, 2024 at 2:10 am
Anonymous
As of 2024, all links in all polymath 8 related blog posts are broken. Is the paper published?
7 January, 2024 at 2:58 am
frobitz13
The first paper (from polymath8a) is here:
https://msp.org/ant/2014/8-9/p03.xhtml
The second paper (from polymath8b) is here: https://link.springer.com/article/10.1186/s40687-014-0012-7