This is a well known problem (see for instance this survey) in the area of “quantum chaos” or “quantum unique ergodicity”; I am attracted to it both for its simplicity of statement (which I will get to eventually), and also because it focuses on one of the key weaknesses in our current understanding of the Laplacian, namely is that it is difficult with the tools we know to distinguish between eigenfunctions (exact solutions to ) and quasimodes (approximate solutions to the same equation), unless one is willing to work with generic energy levels rather than specific energy levels.
The Bunimovich stadium is the name given to any planar domain consisting of a rectangle bounded at both ends by semicircles. Thus the stadium has two flat edges (which are traditionally drawn horizontally) and two round edges, as this picture from Wikipedia shows:

Despite the simple nature of this domain, the stadium enjoys some interesting classical and quantum dynamics. The classical dynamics, or billiard dynamics on is ergodic (as shown by Bunimovich) but not uniquely ergodic. In more detail: we say the dynamics is ergodic because a billiard ball with randomly chosen initial position and velocity (as depicted above) will, over time, be uniformly distributed across the billiard (as well as in the energy surface of the phase space of the billiard). On the other hand, we say that the dynamics is not uniquely ergodic because there do exist some exceptional choices of initial position and velocity for which one does not have uniform distribution, namely the vertical trajectories in which the billiard reflects orthogonally off of the two flat edges indefinitely.
Rather than working with (classical) individual trajectories, one can also work with (classical) invariant ensembles – probability distributions in phase space which are invariant under the billiard dynamics. Ergodicity then says that (at a fixed energy) there are no invariant absolutely continuous ensemble other than the obvious one, namely the probability distribution with uniformly distributed position and velocity direction. On the other hand, unique ergodicity would say the same thing but dropping the “absolutely continuous” – but each vertical bouncing ball mode creates a singular invariant ensemble along that mode, so the stadium is not uniquely ergodic.
Now from physical considerations we expect the quantum dynamics of a system to have similar qualitative properties as the classical dynamics; this can be made precise in many cases by the mathematical theories of semi-classical analysis and microlocal analysis. The quantum analogue of the dynamics of classical ensembles is the dynamics of the Schrödinger equation , where we impose Dirichlet boundary conditions (one can also impose Neumann conditions if desired, the problems seem roughly the same). The quantum analogue of an invariant ensemble is a single eigenfunction
, which we normalise in the usual
manner, so that
. (Due to the compactness of the domain
, the set of eigenvalues
of the Laplacian
is discrete and goes to infinity, though there is some multiplicity arising from the symmetries of the stadium. These eigenvalues are the same eigenvalues that show up in the famous “can you hear the shape of a drum?” problem.) Roughly speaking, quantum ergodicity is then the statement that almost all eigenfunctions are uniformly distributed in physical space (as well as in the energy surface of phase space), whereas quantum unique ergodicity (QUE) is the statement that all eigenfunctions are uniformly distributed. In particular:
- If quantum ergodicity holds, then for any open subset
we have
as
, provided we exclude a set of exceptional k of density zero.
- If quantum unique ergodicity holds, then we have the same statement as before, except that we do not need to exclude the exceptional set.
(In fact, quantum ergodicity and quantum unique ergodicity say somewhat stronger things than the above two statements, but I would need tools such as pseudodifferential operators to describe these more technical statements, and so I will not do so here.)
Now it turns out that for the stadium, quantum ergodicity is known to be true; this specific result was first obtained by Gérard and Leichtman, although “classical ergodicity implies quantum ergodicity” results of this type go back to Schnirelman (see also Zelditch and Colin de Verdière). These results are established by microlocal analysis methods, which basically proceed by aggregating all the eigenfunctions together into a single object (e.g. a heat kernel, or some other function of the Laplacian) and then analysing the resulting aggregate semiclassically. It is because of this aggregation that one only gets to control almost all eigenfunctions, rather than all eigenfunctions. Here is a picture of a typical eigenfunction for the stadium (from Douglas Stone’s page):

In analogy to the above theory, one generally expects classical unique ergodicity should correspond to QUE. For instance, there is the famous (and very difficult) quantum unique ergodicity conjecture of Rudnick and Sarnak, which asserts that QUE holds for all compact manifolds without boundary with negative sectional curvature. This conjecture will not be discussed here (it would warrant an entire post in itself, and I would not be the best placed to write it). Instead, we focus on the Bunimovich stadium. The stadium is clearly not classically uniquely ergodic due to the vertical bouncing ball modes, and so one would conjecture that it is not QUE either. In fact one conjectures the slightly stronger statement:
- Scarring conjecture: there exists a subset
and a sequence
of eigenfunctions with
, such that
does not converge to
. Informally, the eigenfunctions either concentrate (or “scar”) in A, or on the complement of A.
Indeed, one expects to take A to be a union of vertical bouncing ball trajectories (from Egorov’s theorem (in microlocal analysis, not the one in real analysis), this is almost the only choice). This type of failure of QUE even in the presence of quantum ergodicity has already been observed for some simpler systems, such as the Arnold cat map. Some further discussion of this conjecture can be found here. Here are some pictures from Arnd Bäcker‘s page of some eigenfunctions (displaying just one quarter of the stadium to save space) which seem to exhibit scarring:

Of course, each of these eigenfunctions has a fixed finite energy, and so these numerics do not directly establish the scarring conjecture, which is a statement about the asymptotic limit as the energy becomes infinite.
One reason this conjecture appeals to me (apart from all the gratuitous pretty pictures one can mention while discussing it) is that there is a very plausible physical argument, due to Heller and refined by Zelditch, which indicates the conjecture is almost certainly true. Roughly speaking, it runs as follows. Using the rectangular part of the stadium, it is easy to construct (high-energy) quasimodes of order 0 which scar (concentrate on a proper subset A of ) – roughly speaking, these are solutions u to an approximate eigenfunction equation
for some
. For instance, if the two horizontal edges of the stadium lie on the lines y=0 and y=1, then one can take
and
for some large integer n and some suitable bump function
. Using the spectral theorem, one expects u to concentrate its energy in the band
. On the other hand, in two dimensions the Weyl law for distribution of eigenvalues asserts that the eigenvalues have an average spacing comparable to 1. If (and this is the non-rigorous part) this average spacing also holds on a typical band
, this shows that the above quasimode is essentially generated by only O(1) eigenfunctions. Thus, by the pigeonhole principle (or more precisely, Pythagoras’ theorem), at least one of the eigenfunctions must exhibit scarring.
[Update, Mar 28: As Greg Kuperberg pointed out, I oversimplified the above argument. The quasimode is so weak that the eigenfunctions that comprise it could in fact spread out (as per the uncertainty principle) and fill out the whole stadium. However, if one looks in momentum space rather than physical space, the scarring of the quasimode is so strong that it must persist to one of the eigenfunctions, leading to failure of QUE even if this may not quite be detectable purely in the physical space sense described above.]
The big gap in this argument is that nobody knows how to take the Weyl law (which is proven by the microlocal analysis approach, i.e. aggregate all the eigenstates together and study the combined object) and localise it to such an extremely sparse set of narrow energy bands. (Using the standard error term in Weyl’s law one can localise to bands of width O(n) around, say, , and by using the ergodicity one can squeeze this down to o(n), but to even get control on a band of with width
would require a heroic effort (analogous to establishing a zero-free region
for the Riemann zeta function). The enemy is somehow that around each energy level
, a lot of exotic eigenfunctions spontaneously appear, which manage to dissipate away the bouncing ball quasimodes into a sea of quantum chaos. This is exceedingly unlikely to happen, but we do not seem to have tools available to rule it out.
One indication that the problem is not going to be entirely trivial is that one can show (basically by unique continuation or control theory arguments) that no pure eigenfunction can be solely concentrated within the rectangular portion of the stadium (where all the vertical bouncing ball modes are); a significant portion of the energy must leak out into the two “wings” (or at least into arbitrarily small neighbourhoods of these wings). This was established by Burq and Zworski.
On the other hand, the stadium is a very simple object – it is one of the simplest and most symmetric domains for which we cannot actually compute eigenfunctions or eigenvalues explicitly. It is tempting to just discard all the microlocal analysis and just try to construct eigenfunctions by brute force. But this has proven to be surprisingly difficult; indeed, despite decades of sustained study into the eigenfunctions of Laplacians (given their many applications to PDE, to number theory, to geometry, etc.) we still do not know very much about the shape and size of any specific eigenfunction for a general manifold, although we know plenty about the average-case behaviour (via microlocal analysis) and also know the worst-case behaviour (by Sobolev embedding or restriction theorem type tools). This conjecture is one of the simplest conjectures which would force us to develop a new tool for understanding eigenfunctions, which could then conceivably have a major impact on many areas of analysis.
One might consider modifying the stadium in order to make scarring easier to show, for instance by selecting the dimensions of the stadium appropriately (e.g. obeying a Diophantine condition), or adding a potential or magnetic term to the equation, or perhaps even changing the metric or topology. To have even a single rigorous example of a reasonable geometric operator for which scarring occurs despite the presence of quantum ergodicity would be quite remarkable, as any such result would have to involve a method that can deal with a very rare set of special eigenfunctions in a manner quite different from the generic eigenfunction.
Actually, it is already interesting to see if one can find better quasimodes than the ones listed above which exhibit scarring, i.e. to improve the O(1) error in the spectral bandwidth. My good friend Maciej Zworski has offered a dinner in a good French restaurant for this precise problem, as well as a dinner in a very good French restaurant for the full scarring conjecture. (While I may not know as many three-star restaurants as Maciej, I can certainly offer a nice all-expenses-paid trip to sunny Los Angeles for anyone who achieves a breakthrough on any of the open problems listed here. ;-) ).

36 comments
Comments feed for this article
28 March, 2007 at 8:45 am
Greg Kuperberg
I am not sure whether this is a helpful suggestion for actually proving this conjecture, but let me ask whether the following stronger version appears to be the truth.
Suppose that you start with an eigenstate of a rectangle, whose Laplacian can of course be solved explicitly. Not just any eigenstate, but one whose momentum is almost entirely vertical; the horizontal quantum number is the smallest possible. Then suppose that you continuously bulge the sides of the rectangle, say by attaching half-ellipses whose horizontal semiradii grow from 0 to half the height of the rectangle. There should be a spectral flow. Do the eigenstates in question flow to counterexamples to QUE?
28 March, 2007 at 8:48 am
thomas1111
Very naive question: is there any chance to ever know about “the shape and size of specific eigenfunctions for a general manifold” since there might not be analytical ways of expressing them in closed form, except in highly non-generic cases (just like the Galois theory story for roots of polynomials) ?
(Aside comment: isn’t there a latex formula missing in the paragraph “The big gap…” after “but to even get control…”)
28 March, 2007 at 8:50 am
Greg Kuperberg
NB — there may be geometrically easier ways to do the spectral flow. The question of course has both quantum and classical interpretations. You can imagine a stadium drumhead, for example. If the semicircular sides are covered with heavy rubber mats, then the drumhead reduces to a rectangle. But now you can shave rubber mats continuously until they disappear. Again, the question is whether a vertical mode flows to a scarred state.
28 March, 2007 at 9:04 am
Terence Tao
Dear Thomas: thanks for the correction, I think I fixed it. It is true that, like many other PDE questions, exact closed-form solutions are probably impossible. But that doesn’t necessarily prevent us from establishing more “fuzzy” properties of these solutions, such as their size in various function space norms, or how they are distributed in space, indeed much of the previous century’s work in PDE was (and still is) devoted to these sorts of questions. For instance, we understand very well how large these eigenfunctions will be in the Sobolev norms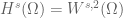 , which describe the regularity of these eigenfunctions, although our understanding of the
, which describe the regularity of these eigenfunctions, although our understanding of the 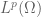 norms, which describe the distribution of these eigenfunctions, is still far from satisfactory.
norms, which describe the distribution of these eigenfunctions, is still far from satisfactory.
Greg: this is an interesting suggestion. There is a problem when two eigenvalues come close to colliding, at which point the spectral flow can become very unstable; a scarred state may end up switching identities with a non-scarred state that it nearly collides with (sort of a quantum version of an elastic collision). I haven’t done the requisite dimensional analysis back-of-the-envelope calculation, but I would imagine that the number of near-collisions one would experience over the lifetime of the deformation would be a positive power of the energy, making it almost hopeless to maintain control of the final state in terms of the initial state. One might hope that the effect of all these collisions cancel themselves out (some sort of quantum second law of thermodynamics), but this brings us back to the seemingly intractable problem of how to show that deterministic dynamical systems exhibit pseudorandom behaviour, which as I mentioned in the Navier-Stokes post is a basic problem which plagues a lot of modern analysis.
28 March, 2007 at 9:15 am
Greg Kuperberg
I would even have to learn how to do such a dimensional analysis, but even if it is unfavorable, it seems possible that the vertical modes are protected by their emergent translational symmetry. (That is, the mode locally looks more and more like f(x)sin(ky), which has a translational symmetry in the y direction.)
Life would be a little cruel if you can’t find a spectral flow that even works numerically. Spectral flow is related to one’s faith in the quasimodes in the first place.
28 March, 2007 at 9:27 am
Terence Tao
Greg, that’s a good point. Though the interesting thing is that the quasimode f(x) sin(ky) does not seem to be concentrated in a single pure mode, but is instead a superposition of O(1) pure modes; conversely, each pure mode consists only partly of the translation-symmetric quasimode but also has a significant fraction of chaotic junk as well. The basic problem is that in the quasimode, f(x) needs to vanish to high order near both open ends of the rectangle; however, to be a pure mode, f(x) “wants” to be an eigenfunction of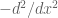 . These two facts are incompatible (since f of course needs to be non-zero). However, because smooth compactly supported functions have rapidly convergent Fourier series, one can express f(x) as a very rapidly convergent sum of pure modes of the interval, and so by analogy we expect something similar in the stadium.
. These two facts are incompatible (since f of course needs to be non-zero). However, because smooth compactly supported functions have rapidly convergent Fourier series, one can express f(x) as a very rapidly convergent sum of pure modes of the interval, and so by analogy we expect something similar in the stadium.
So the spectral dynamics should not be spread out over a huge-dimensional space, but instead should be focused on some low-dimensional “cabal” of O(1) modes, which trade fragments of the quasimode between themselves. This makes things a bit more promising, though it’s still not clear how to proceed. Perhaps one approach is not to focus on a single mode but rather on the space spanned by all the relevant modes (or maybe some associated projection operator, i.e. a mixed state rather than a pure state). This may be a bit more stable than trying to evolve a single mode.
Part of the problem stems from the fact that the operator , despite appearances, does not actually commute with the Laplacian
, despite appearances, does not actually commute with the Laplacian 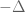 , due to effects coming from the non-horizontal portions of the boundary. One can localize that operator to within the rectangle with a cutoff function, but then it is the cutoff which doesn’t commute with the Laplacian. Indeed the uncertainty principle then forces a spectral spreading of O(1), as discussed in the main post, which by the Weyl law heuristic then incorporates a non-trivial number of pure modes (indeed, even in the rectangle, the quasimode f(x) sin ny is split up among the pure modes sin mx sin ny for m = O(1)). If one could tighten the spectral bandwidth from O(1) to o(1) then one might be in much better shape, but this is already looking difficult.
, due to effects coming from the non-horizontal portions of the boundary. One can localize that operator to within the rectangle with a cutoff function, but then it is the cutoff which doesn’t commute with the Laplacian. Indeed the uncertainty principle then forces a spectral spreading of O(1), as discussed in the main post, which by the Weyl law heuristic then incorporates a non-trivial number of pure modes (indeed, even in the rectangle, the quasimode f(x) sin ny is split up among the pure modes sin mx sin ny for m = O(1)). If one could tighten the spectral bandwidth from O(1) to o(1) then one might be in much better shape, but this is already looking difficult.
28 March, 2007 at 9:35 am
Greg Kuperberg
I can’t quite tell if you’re still saying that spectral flow stories are outright false (you won’t sustain scarring) or merely difficult to prove. You could also be saying that spectral flow is a spurious model on the grounds thta whathever you could prove with it, you could also prove without it.
28 March, 2007 at 9:38 am
Greg Kuperberg
Oh, sorry, I read the middle paragraph more closely; I get the discussion now.
28 March, 2007 at 9:59 am
Terence Tao
Greg, my guess is that you will have to somehow get either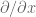 or
or  involved in the spectral flow equation (which will force one to leave the world of single pure modes and work with more mixed objects), otherwise one will be faced with the identity switching problem.
involved in the spectral flow equation (which will force one to leave the world of single pure modes and work with more mixed objects), otherwise one will be faced with the identity switching problem.
A model case may illustrate the issue. Let A and B be two Hermitian matrices of size n, and consider their direct sum , which is of size 2n. The spectrum of this sum is simply the union of the spectra of A and B. Now suppose we evolve A and B until one of the eigenvalues of A crosses one of the eigenvalues of B. What happens to the eigenstate of A under naive spectral flow in this case? Well, the flow becomes singular at the moment of collision.
, which is of size 2n. The spectrum of this sum is simply the union of the spectra of A and B. Now suppose we evolve A and B until one of the eigenvalues of A crosses one of the eigenvalues of B. What happens to the eigenstate of A under naive spectral flow in this case? Well, the flow becomes singular at the moment of collision.
But this is a highly non-generic case. Suppose we now add an epsilon of noise to the direct sum. This lets one avoid the codimension-2 set where eigenvalues collide; instead, the eigenvalues will bounce off of each other after getting within epsilon (or maybe square root of epsilon) of each other (the famous repulsion-of-eigenvalues effect). But then, if we evolve eigenvalues continuously, an eigenvalue which was previously close to an eigenvalue of A, would become something close to an eigenvalue of B instead after a collision; hence, an eigenstate close to an eigenstate of A will, after the collision, flow to an eigenstate close to that of B. The state which was close to that of A is now assigned to an eigenvalue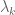 with a different value of k, because of the crossing. There has been an identity switch.
with a different value of k, because of the crossing. There has been an identity switch.
My guess is that a numerical scheme which somehow can detect when this switching has occurred (e.g. by using the above momentum operators) may be fairly stable. As long as only O(1) pure modes are present in the spectral band of the quasimode, things should be OK. As mentioned in the main post, though, the enemy is if the special energy levels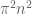 have some very weird “attractor” property, in that many more eigenvalues get attracted to these levels than Weyl’s law would predict. One can’t have too many (more than n) in this band, as that really would contradict Weyl’s law, but with our current understanding of the error term in Weyl’s law (and even with the conjectured best bounds on this term) one still can have far too many modes in this band for comfort. This shouldn’t happen, at least for generic values of n, but I have no idea how to prove that would be the case.
have some very weird “attractor” property, in that many more eigenvalues get attracted to these levels than Weyl’s law would predict. One can’t have too many (more than n) in this band, as that really would contradict Weyl’s law, but with our current understanding of the error term in Weyl’s law (and even with the conjectured best bounds on this term) one still can have far too many modes in this band for comfort. This shouldn’t happen, at least for generic values of n, but I have no idea how to prove that would be the case.
Incidentally, one can phrase this problem as a question of determining how stable the method of separation of variables is in solving PDE. This method trivially lets us determine the eigenfunctions of a rectangle; why shouldn’t some variant of it still give some control on eigenfunctions of a near-rectangle?
28 March, 2007 at 1:45 pm
Greg Kuperberg
I certainly understand that symmetric matrices with eigenvalue multiplicity have codimension 2, that Hermitian matrices with multiplicity have codimension 3, and that spectral flow can end up permuting the eigenvalues adversarilally. These principles show up, for example, in adiabatic quantum computing.
I think that you and may agree that there could be truths about spectral flows that could make this problem easier to solve, unlike for example the Navier-Stokes question, where a variety of truths are known to make the problem harder to solve.
28 March, 2007 at 2:03 pm
Terence Tao
Oops, you’re right; the codimension in the Hermitian case is indeed 3, not 2.
Certainly I rate this question as significantly easier than Navier-Stokes – not that that is really saying all that much. The problem here is one of linear constant coefficient elliptic PDE, rather than a nonlinear parabolic PDE, and the domain is about as simple as one can get without actually being able to get explicit closed-form solutions. The domain even has a little bit of symmetry, though this is unlikely to be terribly useful (and it does cause a minor amount of headache here, for instance many of the eigenvalues here will acquire some trivial multiplicity due to the symmetries).
Spectral flows are very pretty, but the fact that they don’t react well to eigenvalue collisions or multiplicity is somewhat disconcerting. It comes down to the fact that, from a functional calculus point of view, it doesn’t actually make much sense to talk about things like “the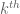 eigenfunction”, because this doesn’t depend smoothly on the operator when multiplicity occurs. Whereas aggregate objects such as heat kernels, resolvents, wave propagators, etc. are much more robust, and make a lot more sense from the functional calculus perspective. So we can control eigenmodes on the average by very stable and robust methods, but it isn’t obvious that we can do something similar for individual eigenmodes.
eigenfunction”, because this doesn’t depend smoothly on the operator when multiplicity occurs. Whereas aggregate objects such as heat kernels, resolvents, wave propagators, etc. are much more robust, and make a lot more sense from the functional calculus perspective. So we can control eigenmodes on the average by very stable and robust methods, but it isn’t obvious that we can do something similar for individual eigenmodes.
Perhaps one needs to transform the question to a very different looking question which looks more stable. For instance, it is tempting to perform a Fourier expansion inside the rectangle and a spherical harmonic expansion (i.e. a Fourier expansion in polar coordinates) in the wings. Matching the two boundaries leads to a problem which looks very vaguely like an Anderson localisation problem, which is a fairly stable phenomenon in generic cases. I played around with this a bit in the past but didn’t really get anywhere, though.
28 March, 2007 at 7:34 pm
Greg Kuperberg
Actually there is something that I don’t quite understand about the existence argument that you credit to Heller and Zelditch. Is it supposed to apply to rectangles? At first glance, most rectangles do satisfy QUE.
28 March, 2007 at 7:53 pm
Terence Tao
Hmm, you’re right, I oversimplified the argument a bit.
It’s true that for rectangles with irrational sidelengths, all eigenfunctions, being plane waves, are uniformly distributed in physical space. I was hiding however the full definition of QUE – one has to look at the distribution of the eigenfunctions not just in physical space, but in momentum space and more generally in phase space. The plane waves are incredibly highly concentrated in momentum space, and rectangles are not quantum ergodic (which is unsurprising given that they are also not classically ergodic).
The formal definition of quantum ergodicity and QUE is a little technical; one can ask that the Wigner transform of the eigenfunction, suitably normalised, converges weakly to the uniform distribution; or one can ask that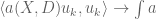 for all pseudo-differential operators (or quantum observables, if you will) a(X,D) of order 0, where
for all pseudo-differential operators (or quantum observables, if you will) a(X,D) of order 0, where  is the integral of the symbol of a on the energy surface (the cosphere bundle). More informally, you want to see “quantum chaos” – the eigenfunction should be in all positions and all momenta at once.
is the integral of the symbol of a on the energy surface (the cosphere bundle). More informally, you want to see “quantum chaos” – the eigenfunction should be in all positions and all momenta at once.
The Heller-Zelditch argument for the rectangle would start with a quasimode, which is highly concentrated in frequency space (aka momentum space), and conclude the existence of pure modes with the same property; this would count as scarring, albeit in frequency space rather than physical space. One could pull something similar off in the stadium, provided that there are not too many eigenvalues in the relevant spectral band.
28 March, 2007 at 11:29 pm
Greg Kuperberg
With these remarks, I only have more trouble believing the story of out-of-control spectral flow. That story makes a lot of sense for many kinds of spectral flow, for example an overly optimistic adiabatic quantum algorithm. But in this case, suppose that you have a particle in a convex region which is somehow a pregnant rectangle. (A regular hexagon, a stadium, etc.) If a state is highly localized in momentum space, perpendicular to the parallel sides, then the pregnant regions in position space have to be blank. But if these regions are blank, then it is stable as you reshape the pregnant sides. If you execute spectral flow from a perfect rectangle, then the momentum must delocalize either fairly quickly or not at all.
29 March, 2007 at 7:12 am
Terence Tao
Dear Greg, I suppose I should have said “concentrated” in frequency space rather than “localised”; the particle has a significant portion of its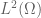 norm located in the vertical frequency, but also a significant portion outside. Look for instance at the second and third eigenfunctions on the final image of the main post. At a PDE level, this is coming from the compatibility condition between the eigenfunction equation on the half-open rectangle (which wants to concentrate vertically) and the semicircular wings (which want to distribute the mode more evenly in phase space). Physically, I guess a quantum particle in this mode spends part of its time resonating vertically, then leaks out to bounce around arbitrarily around the stadium for a while, then returns to resonating vertically. (Of course, one can’t really use classical language to describe a mode like this, so one has to take this analogy with the usual grain of quantum salt.)
norm located in the vertical frequency, but also a significant portion outside. Look for instance at the second and third eigenfunctions on the final image of the main post. At a PDE level, this is coming from the compatibility condition between the eigenfunction equation on the half-open rectangle (which wants to concentrate vertically) and the semicircular wings (which want to distribute the mode more evenly in phase space). Physically, I guess a quantum particle in this mode spends part of its time resonating vertically, then leaks out to bounce around arbitrarily around the stadium for a while, then returns to resonating vertically. (Of course, one can’t really use classical language to describe a mode like this, so one has to take this analogy with the usual grain of quantum salt.)
It’s because of this that I suspect that the spectral flow is going to be rather subtle. As we discussed earlier, the crossing of two eigenvalues of even two totally unrelated modes can cause a switch as long as there is even an epsilon of coupling between the dynamics of the two modes. One has to somehow restrict to the much smaller set of modes which exhibit at least some concentration in the desired vertical frequency before one would get a reasonable dynamics.
29 March, 2007 at 8:40 am
Greg Kuperberg
Sure, if you want me to speak quantumly: x and y momentum are commuting quantum random variables, so you may as well consider them to be classical random variables, unless you were to attempt a joint distribution with variables that they don’t commute with. (*) I agree that no eigenstate of the Hamiltonian can be completely localized in a bounded region around +k and -k in momentum space, nor even localized with exponential decay.
(*) And non-commutation with position is sufficiently gentle that there is a kind of joint distribution, the Wigner function.
However, from two of the example plots, it looks like there exist eigenstates with pretty good momentum localization, i.e., with adequate polynomial bounds. (I admit that I have no idea how good they are.) There also exist eigenstates with less good momentum localization.
I also admit that I have no idea how to rigorously prove any really good theorem in PDEs; I have no practice. That said, I’m going to provocative and conjecture that spectral flow, as you get just by changing the shape of the corral from a square to a stadium, works. I think that it can be simulated without much more difficulty than solving the Laplacian with one shape. If it is really true that the spectral flow is merely subtle and not provably anomalous, then maybe the thing to do is just try it and see. (Could that qualify as agreeing to disagree?)
29 March, 2007 at 9:02 am
Terence Tao
Actually, I can come up with a rigorous argument as to why spectral flow won’t work. The basic problem is that spectral flow preserves the index k of the eigenvalue, which when combined with Weyl’s law will force an energy shift, whilst the quasimode stays at a roughly fixed energy.
Let A(t) be a Hermitian operator depending on a time parameter t; in this case, A(0) might be the Laplacian on the rectangle and A(1) the Laplacian on the stadium, with some continuous deformation in between. (Yeah, I know, the domains aren’t the same. We can fix this in a number of ways, e.g. conformally mapping all domains to a single reference domain, or something.) Suppose is the
is the 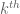 eigenvector and eigenvalue of A(0), normalised in
eigenvector and eigenvalue of A(0), normalised in 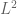 . If we then start spectral flow to create the time-evolved eigenvalues and eigenvectors
. If we then start spectral flow to create the time-evolved eigenvalues and eigenvectors 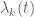 and
and 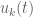 , one observes that barring an actual eigenvalue collision (which is unlikely, since this is a codimension 3 set that one is trying to hit with a dimension 1 trajectory), the eigenvalue
, one observes that barring an actual eigenvalue collision (which is unlikely, since this is a codimension 3 set that one is trying to hit with a dimension 1 trajectory), the eigenvalue 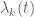 will retain its position as the
will retain its position as the 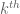 eigenvalue; for instance, we will have
eigenvalue; for instance, we will have  . If there is an eigenvalue collision, then of course the spectral flow becomes singular and the whole strategy is moot anyway.
. If there is an eigenvalue collision, then of course the spectral flow becomes singular and the whole strategy is moot anyway.
Now we have Weyl’s law, which asserts that the number of eigenvalues of a Laplacian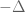 in a domain
in a domain  with eigenvalues less than
with eigenvalues less than  is asymptotically
is asymptotically  . This implies the asymptotic
. This implies the asymptotic  .
.
Now let’s start the spectral flow with the unit square and
the unit square and  , then
, then  and
and  . We flow this to time 1, where
. We flow this to time 1, where  is now the stadium. Because spectral flow preserves k, we still have
is now the stadium. Because spectral flow preserves k, we still have  , so by Weyl’s law the energy has dropped to
, so by Weyl’s law the energy has dropped to 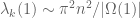 . But the stadium has area strictly larger than that of the square, and so the spectral flow has left one with an eigenstate of energy far lower than the energy band
. But the stadium has area strictly larger than that of the square, and so the spectral flow has left one with an eigenstate of energy far lower than the energy band ![{}[\pi^2 n^2 - O(1), \pi^2 n^2 + O(1)]](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Cpi%5E2+n%5E2+-+O%281%29%2C+%5Cpi%5E2+n%5E2+%2B+O%281%29%5D&bg=ffffff&fg=545454&s=0&c=20201002) where the quasimode
where the quasimode  lives in. Thus the spectral flow has necessarily flowed away from the quasimode.
lives in. Thus the spectral flow has necessarily flowed away from the quasimode.
Now one can try to repair this by flowing from the stadium to a rectangle of equal area to the stadium, which would be better, but I don’t think it fixes things perfectly. The basic problem is that in order for spectral flow to work, the number of eigenvalues less than the eigenvalue of the scarred state in the stadium needs to be exactly equal to the number of eigenvalues less than the eigenvalue of the scarred state in the rectangle. Due to the error term in Weyl’s law, one is unlikely to hit this number exactly on the nose.
p.s. because of the effects of the boundary of the stadium, the x and y momenta operators don’t quite commute, but it’s close enough that one can still meaningfully talk about a joint distribution as long as one doesn’t try to localise to too fine a scale (one is pretty safe as long as one tolerates uncertainties of more than O(1) in both momenta).
29 March, 2007 at 9:44 am
Greg Kuperberg
Actually, I can come up with a rigorous argument as to why spectral flow won’t work. The basic problem is that spectral flow preserves the index k of the eigenvalue, which when combined with Weyl’s law will force an energy shift, whilst the quasimode stays at a roughly fixed energy.
Sigh. I was provocative all right, but I only provoked you to rigorously disprove my thinking. :-( I agree, there is no reason to believe that the qualitative attributes of the eigenvalues are strictly compatible with their ordering.
You’re absolutely right, it takes more thought to properly select the right eigenstates under any kind of spectral flow. Even a low-dimensional space of eigenstates is not good enough, by the same ordering argument. It could perhaps be interesting if you thought of a joint spectral flow of some kind involving two or more commuting operators. It isn’t worth a numerical simulation without more thought.
p.s. because of the effects of the boundary of the stadium, the x and y momenta operators don’t quite commute
Okay, this one is a purely semantic point, but I maintain that d/dx and d/dy do commute with each other. What you are saying is that they don’t quite commute with the Hamiltonian. That is perfectly true, but what it means is that when the Hamiltonian is definite, d/dx and d/dy have a (joint) distribution.
29 March, 2007 at 10:44 am
Terence Tao
Okay, this one is a purely semantic point, but I maintain that d/dx and d/dy do commute with each other. What you are saying is that they don’t quite commute with the Hamiltonian. That is perfectly true, but what it means is that when the Hamiltonian is definite, d/dx and d/dy have a (joint) distribution.
This point confused me for a long time when I first learnt it, but just because d/dx and d/dy commute on a dense subspace of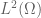 , e.g. the smooth functions supported on a compact subset of the interior, does not mean that their functional calculi commute with each other. You can see this already by thinking about the eigenfunction equations for d/dx and d/dy. (These operators are not elliptic and so don’t have discrete spectrum, but this exercise is illuminating nonetheless.) To be an eigenfunction for d/dx, the eigenfunction must look like a sine wave on each horizontal slice of the stadium. Similarly, to be an eigenfunction for d/dy, the eigenfunction must look like a sine wave on each vertical slice. Due to the funny geometry of the stadium and the Dirichlet boundary conditions, these two conditions are incompatible.
, e.g. the smooth functions supported on a compact subset of the interior, does not mean that their functional calculi commute with each other. You can see this already by thinking about the eigenfunction equations for d/dx and d/dy. (These operators are not elliptic and so don’t have discrete spectrum, but this exercise is illuminating nonetheless.) To be an eigenfunction for d/dx, the eigenfunction must look like a sine wave on each horizontal slice of the stadium. Similarly, to be an eigenfunction for d/dy, the eigenfunction must look like a sine wave on each vertical slice. Due to the funny geometry of the stadium and the Dirichlet boundary conditions, these two conditions are incompatible.
In fact there is a nice theorem of Fuglede which asserts that on a domain , the partial derivative operators
, the partial derivative operators  have a joint functional calculus if and only if
have a joint functional calculus if and only if 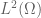 enjoys an orthonormal basis consisting entirely of (normalised) plane waves. He then conjectured that this latter condition holds if and only if
enjoys an orthonormal basis consisting entirely of (normalised) plane waves. He then conjectured that this latter condition holds if and only if  tiles Euclidean space by translations (note that the stadium manifestly does not have this property, whereas the rectangle does). This conjecture was proven for convex bodies in the plane by Iosevich, Katz, and myself, but is false in higher dimensions (a result of myself, as well as one of Kolountzakis and Matolcsi).
tiles Euclidean space by translations (note that the stadium manifestly does not have this property, whereas the rectangle does). This conjecture was proven for convex bodies in the plane by Iosevich, Katz, and myself, but is false in higher dimensions (a result of myself, as well as one of Kolountzakis and Matolcsi).
29 March, 2007 at 11:01 am
Greg Kuperberg
My conventions are a bit different from this, but I believe that they work. Instead of looking at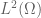 , I would still define
, I would still define  as operators on
as operators on  . Then they do commute exactly and have a meaningful joint distribution.
. Then they do commute exactly and have a meaningful joint distribution.
Now you could object that the Hamiltonian does not make sense on this larger Hilbert space. But you can extend it to an operator whose spectrum lies in
does not make sense on this larger Hilbert space. But you can extend it to an operator whose spectrum lies in ![[0,\infty]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) , by assigning infinite energy to any state outside
, by assigning infinite energy to any state outside  . Another way to describe
. Another way to describe  is that
is that  is a perfectly good bounded operator.
is a perfectly good bounded operator.
Another way to describe the momenta is that the projection from to
to 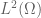 changes
changes  from a Hermitian operator to a POVM (on the smaller Hilbert space,
from a Hermitian operator to a POVM (on the smaller Hilbert space, 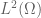 ). The POVMs still commute.
). The POVMs still commute.
Now, your operators are also perfectly valid mathematically, although I think that they are not self-adjoint (or rather, non-normal) due to the boundary conditions. If so, they are technically not allowed as quantum random variables. However, you may have reason to like them better otherwise for the purpose of obtaining estimates in analysis.
are also perfectly valid mathematically, although I think that they are not self-adjoint (or rather, non-normal) due to the boundary conditions. If so, they are technically not allowed as quantum random variables. However, you may have reason to like them better otherwise for the purpose of obtaining estimates in analysis.
29 March, 2007 at 11:06 am
Greg Kuperberg
The POVMs still commute.
Sorry, argh, they probably do not. But they have a mutual refinement, a positive operator-valued measure from momentum-space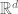 to
to 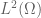 . That’s the real trick: POVMs don’t strictly have to commute to admit a mutual refinement.
. That’s the real trick: POVMs don’t strictly have to commute to admit a mutual refinement.
31 March, 2007 at 9:27 pm
Gil Kalai
Is there a way to define/explain quantum ergodicity and quantum unique ergodicity in the context of graph Laplacians? (I suppose that since these are asymptotic properties they apply to sequences of graphs rather than a single graph; like the notion of expanders.)
31 March, 2007 at 10:29 pm
Terence Tao
Dear Gil, I believe the analogous notions for graph Laplacians are as follows. Let be a graph sequence of increasingly large graphs; one should probably think of these graphs as having bounded degree, with polynomial growth of metric balls, otherwise the concepts below are likely to be trivial or useless. For each fixed k, let
be a graph sequence of increasingly large graphs; one should probably think of these graphs as having bounded degree, with polynomial growth of metric balls, otherwise the concepts below are likely to be trivial or useless. For each fixed k, let 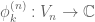 be the
be the 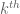 eigenfunction of
eigenfunction of  , normalised to have
, normalised to have  norm equal to 1. Then one would say that the graph sequence is quantum uniquely ergodic if for each k, the eigenfunction density
norm equal to 1. Then one would say that the graph sequence is quantum uniquely ergodic if for each k, the eigenfunction density  is asymptotically uniformly distributed on large balls
is asymptotically uniformly distributed on large balls 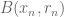 in the graph metric, thus for arbitrary choices of
in the graph metric, thus for arbitrary choices of 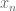 and
and 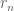 we have
we have
as n goes to infinity (with k kept fixed). Quantum ergodicity would be the same statement but one would be allowed to exclude a set of k’s of density zero. For instance, a graph sequence which was disconnected with multiple components of positive density would not be quantum ergodic or quantum uniquely ergodic in the above senses.
I believe (but haven’t checked the details) that the above notions of quantum ergodicity (ignoring for now the technical distinction between physical space and phase space) correspond to the continuous notions defined above if we discretise the domain in the obvious manner, namely replacing the domain by the finite set
in the obvious manner, namely replacing the domain by the finite set  for some large n, and then connecting any pair of adjacent vertices in this set (separated by either a horizontal or vertical displacement of 1/n) by an edge to form the graph
for some large n, and then connecting any pair of adjacent vertices in this set (separated by either a horizontal or vertical displacement of 1/n) by an edge to form the graph  .
.
Incidentally, there appears to be some literature on “quantum graphs”, for which notions of quantum ergodicity and quantum unique ergodicity can be defined, but this seems to be a slightly different concept.
1 April, 2007 at 11:02 pm
Gil Kalai
Thanks, Terry. Usually the graph of the discrete cube is an interesting example to look at/start with. Here, with the naive definition it has QUE because all entries of all eigenvalues are plus or minus one. I suspect that with the notion of “phase spece” you referred to, it might be decorated with many scarrs related to its faces to the extent of desrving the title “scarface”. So maybe the discrete cube is a good example to demonstrate these notions and extra subtelties.
2 April, 2007 at 8:36 am
Terence Tao
Dear Gil,
I don’t think I can transplant the notion of phase space properly to the graph theory setting; I would need some notion of “momentum” or “frequency” to assign to the eigenfunction, which seems to require a Riemannian geometry structure (which one needs to define the notion of a plane wave). We do have a metric coming from the graph, but it isn’t obviously Riemannian unless one adds additional structure to the graph (e.g. one embeds it into a Riemannian manifold, such as the stadium, but then we are leaving graph theory and returning to geometry). The faces are not exactly the problem; for the discretised torus one also gets eigenfunctions which are evenly distributed in physical space but are highly localised in momentum space. (I do like the term “scarface” though, I wish I could cook up some situation where I coud introduce the term naturally. :-) )
15 April, 2007 at 12:21 pm
barry Friedman
In the quantum case, is there some “physically observable” consequence for the existence of the scar states at “arbitrarily” high energy?
For classical billiards, such physical observables exist. For example, for the Sinai billiard, looking at the velocity autocorrelation function
(vacf) averaged over the microcanonical ensemble distinguishes the case of bounded and unbounded horizon. for unbounded horizon the vacf decays with a power law vs the exponential decay in the bounded horizon case. the difference in the 2 situations is the presence of arbitrarily long trajectories that don’t collide with the central obstacle. (analogous to the bouncing ball trajectories in the stadium). even though these initial conditions have zero measure, they still make themselves felt in certain averaged quantities.
Does something of this nature occur in the quantum case ?
16 April, 2007 at 10:13 am
Terence Tao
Dear Barry,
A good question! I’m not entirely sure as to the answer. The thing is that (a) the scarred states will be very infrequent, as we know that almost all of the eigenstates do not exhibit scarring, and (b) there are also a large number of scarred quasimodes which behave physically like scarred states under either the wave equation or Schrodinger equation for bounded amounts of time, and could thus “spoof” the scarred states on these intervals. However it may be that the very long time singularity propagation behaviour of either the wave or Schrodinger equation may hinge on the existence of scarred states; if there are many such states one could imagine that a wave which is initially singular on a periodic trajectory (e.g. take a horizontal wave front moving vertically) will retain some residual version of that singularity for indefinite periods of time, whereas in the absence of scarring this singularity will eventually be “evenly distributed” across phase space, whatever that means. I don’t have a rigorous version of this statement though.
3 May, 2007 at 8:32 pm
Dima Jakobson
Hi Terry, one can define classical dynamics for graphs, this will just be a random walk. One can also define directions, just look at oriented edges (take a line graph). You can put weights on them, this will define the metric etc. You can write laplacian as d*d, where d would be the difference operator (that’s how Kirckhoff’s theorem can be proved). About uniform distribution, one should (as you suggest) take a sequence of graphs of growing size, and call it ergodic if “almost all” eigenvectors become equidistributed (as the size of the graph grows). This seems like a nice “random graph” problem. Btway, here is my favorite question about the spectrum of random regular graphs: is it simple (you are not allowed to put weights on the edges, of course)?
About scarring in different systems: the best understood case seems to be (quantum) cat maps, where you have both examples of scars (due to De Bievre, Faure and Nonnenmacher), and “non-scarring” results of Kurlberg-Rudnick. In the continuous case, the best chance for scarring is either Bunimovich stadium or Donnelly’s examples; in other situations (e.g. for Sinai billiard or in strictly negative curvature) you have much less chance.
7 July, 2008 at 10:58 pm
Hassell’s proof of scarring for the Bunimovich stadium « What’s new
[…] series (now long since on hiatus), I featured one of my favorite problems, namely that of establishing scarring for the Bunimovich stadium. I’m now happy to say that this problem has been solved (for generic stadiums, at least, […]
26 January, 2009 at 7:40 am
Michael Nielsen » Doing science online
[…] Tao has hundreds of other posts, on topics like Perelman’s proof of the Poincare conjecture, quantum chaos, and gauge theory. Many posts contain remarkable insights, often related to open research problems, […]
28 April, 2016 at 2:41 am
Anonymous
Hope you’re still reading these – the figures on this article seem to be broken, hopefully they’re still kicking around somewhere and can be fixed.
[Unfortunately the sites linked to seem to no longer have the images. -T.]
29 April, 2016 at 1:13 pm
Anonymous
Everybody can still see the images via the (Internet Archive) Wayback Machine and Terry, if you want, throught it, you can also save a copy of each of them and restore them inside this post. [Just my two cents, hope this helps.]
13 November, 2016 at 6:14 pm
John Baez
By the way, the picture “Scarring eigenfunctions” has disappeared from this blog post, leaving those words.
22 January, 2017 at 10:33 am
Polygonal billiards | Bahçemizi Yetiştermeliyiz
[…] The Bunimovich stadium is an example of a dynamical system—a planar billiard, in fact, although not polygonal—which is known to be ergodic but not uniquely ergodic. […]
1 October, 2017 at 6:48 pm
Хаос: эффект бабочки, фигуры Хладни и тайны мироздания | ТЕХНОЛОГИИ, ИНЖИНИРИНГ, ИННОВАЦИИ
[…] Примеры профилей амплитуд колебаний в стоячих волнах в хаотических квантовых бильярдах «улитка Паскаля» и «стадион». […]
16 May, 2018 at 1:28 am
CL
A somehow related question from a non-mathematician:
Weyl’s conjecture gives us the asymptotic distribution of the eigenvalues $\lambda$ of the Laplace operator in a domain $\Omega$ with homogeneous Dirichlet boundary condition on $\partial \Omega$.
According to this conjecture, the asymptotic distribution of the eigenvalues depends only on the volume and perimeter of the domain. However, I recall having read somewhere that “chaotic” domains (like billiards) support more eigenvalues in the same interval $[\lambda_1,\lambda_2]$ than “regular” domains (like squares, rectangles, circles etc.).
Is this qualitative, somehow vague statement true in any sense? If so, is this due to the degeneracy of some eigenvalues in regular domains, or are there other, “deeper” reasons? I have read that the statistics of the eigenvalue distribution depends on the form and the degree of “chaoticity” of the domain, so maybe this is a plausible reason. Any hint to the literature would be greatly appreciated!