I’m continuing my series of articles for the Princeton Companion to Mathematics with my article on compactness and compactification. This is a fairly recent article for the PCM, which is now at the stage in which most of the specialised articles have been written, and now it is the general articles on topics such as compactness which are being finished up. The topic of this article is self-explanatory; it is a brief and non-technical introduction as to the incredibly useful concept of compactness in topology, analysis, geometry, and other areas mathematics, and the closely related concept of a compactification, which allows one to rigorously take limits of what would otherwise be divergent sequences.
The PCM has an extremely broad scope, covering not just mathematics itself, but the context that mathematics is placed in. To illustrate this, I will mention Michael Harris‘s essay for the Companion, ““Why mathematics?”, you may ask“.
What's new 
23 comments
Comments feed for this article
20 November, 2007 at 5:14 pm
Anonymous
Small typo: in the second line “each the” should be “each of the” .
20 November, 2007 at 5:22 pm
Antonio
Looks like a great article, as usual.
Small error: p. 3, 6th line of paragraph 3: “any compact space has a number of compactifications”. A compact space is already compact. :) Not sure what’s a nice pedagogical way of saying which spaces admit compactifications, without bringing in local compactness so soon.
20 November, 2007 at 8:20 pm
Richard
Thanks for emphasizing the very powerful ultrafilter construction of the Stone-Cech compactification. Correct me if I’m wrong, but I believe that this particular compactification was originally conceived using an approach other than ultrafilters. If so, whose idea was it to use ultrafilters? The earliest use of ultrafilters in this context that I’m aware of was by Robert Ellis in Lectures on Topological Dynamics (1969). (There the focus was on compactifications of discrete groups.) I’ve asked a now retired topologist — someone who has been around for a long time — and they did not know.
21 November, 2007 at 1:57 am
Emmanuel Kowalski
Here’s a typo on the last page line -9 : “in a certain compactifications…”; I’m not sure if the ‘a’ or the ‘s’ at the end of compactification should go…
Also I find interesting that you describe distribution spaces as compactifications; wouldn’t it be more natural to speak of completions here? (Of course there’s a lot of relations between the two concepts).
21 November, 2007 at 5:29 am
Adam
Is then the physical Lorentz weak L^2 also a compactification
(it predicts vortices in phenomena nonlocal in time)?
14 September, 2009 at 1:45 am
David Fremlin
Since he was writing primarily for mathematicians he could well have omitted most of the references to bad philosophy, which we can easily find for ourselves. But the actual content of his article, if you take the trouble to dig for it, is worth considering. In particular, he is on strong ground in maintaining that the concept of “set” (as used by mathematicians) is more fruitful than the concept of “essence” (as used by philosophers).
21 November, 2007 at 3:03 pm
Le fantôme de Descartes.
Michael Harris’s unvolutarily hilarious article chock-full of references to post-modernists like Derrida, Foucault and Lyotard looks like a cross between Sokal’s hoax and an article written by the mischievous random generator of social science texts:
http://www.elsewhere.org/pomo/
Here is a sample of Harris’s prose:
“I would like to argue that the nothing
designated by “set” is somehow different, and more fruitful, than the nothing designated by “essence.” ”
As we say in France: le ridicule ne tue pas , which explains Harris’s survival.
21 November, 2007 at 3:39 pm
Terence Tao
Thanks for all the corrections!
22 November, 2007 at 12:51 am
Confused student
Dear Terence,
your Princeton article explaining compactness as extended finiteness is fantastically illuminating.
Although your birational correspondence between the x-axis and the circle with origin deleted is completely correct, I don’t see how (i.e. from what point on the circle) it is a stereographic projection. Sorry to waste your time with such trivialities.
22 November, 2007 at 4:06 pm
Benoit Jubin
Confused student: the formula for the stereographic projection should be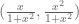
, and the projection is then from the north pole (0,1).
23 November, 2007 at 11:28 am
Confused student
Benoit: what you say is indeed correct, but then the north pole should be removed from the circle, not the origin.
23 November, 2007 at 11:40 am
Terence Tao
Dear confused student and Benoit:
Sorry for the confusion (I had shifted the real line up by one unit in order to take the projection at the origin). I’ve implemented Benoit’s fix (and replaced the origin with (0,1)).
14 January, 2008 at 5:39 am
Michael Harris
The comment of the colleague hiding beneath the modest pseudonym
“Le fantôme de Descartes” seemed to have no ambition other than to
be offensive, but it does suggest it might be useful to clarify the purposes
of my PCM article, in order to avoid misunderstandings. This has been
done here:
http://www.institut.math.jussieu.fr/~harris/onPCM.htm
The point of the quotation chosen to illustrate my style should be
reasonably clear in the context of my article, but I spell it out
in the above link.
6 October, 2008 at 12:01 am
David Corfield
Regarding Le fantôme de Descartes’s comment, a remark Michael Harris’ makes on my work in this piece (or at least the draft I saw) is one of the most perceptive I have ever received. And the tasks with which he charges philosophers, are precisely correct:
‘They also have a duty, it seems to me, to account for terms like “idea” and “intution” – and “conceptual” for that matter – used by human mathematicians (at least) to express their value judgments.’
5 November, 2008 at 5:15 pm
Concentration compactness and the profile decomposition « What’s new
[…] important topological concepts in analysis is that of compactness (as discussed for instance in my Companion article on this topic). There are various flavours of this concept, but let us focus on sequential compactness: a […]
24 November, 2008 at 3:41 am
K. P. Hart
A belated answer to Richard (20 nov, 2007): the use of ultrafilters in the construction of compactifications dates back to Wallman’s work but was made explicit in Gilman and Jerison’s Rings of continuous functions: the Cech-Stone compactification is the space of zero-set ultrafilters. See http://dutiaw37.twi.tudelft.nl/~kp/publications/the_papers/ency/d17-betaX.pdf.pdf and http://dutiaw37.twi.tudelft.nl/~kp/publications/the_papers/ency/d18-betaN-and-betaR.pdf for more information.
24 November, 2008 at 4:02 pm
Richard
K. P. Hart,
Thanks much for the information! It’s a shame when the origin of ideas gets lost over time, so I’m very happy to hear this. The name Wallman rings a bell, and I now have a vague recollection of something that may have been called a “Wallman compactification”, so I’m going to look into that. Ages ago, when in graduate school, a professor recommended that I read Rings of Continuous Functions. Maybe it’s time that I finally follow up on that recommendation!
25 November, 2008 at 4:41 am
K. P. Hart
Richard: you’re most welcome.
For those who got redirected to room 404: here is the correct link to the article on betaX. It’s from the Encyclopedia of General Topology, which also contains an article on Wallman compactifications.
2 November, 2010 at 2:38 am
Ray
Dear Prof. Tao
I have read this helpful article. In the last paragragh you mentioned a idea that one can view a straight line in the plane as the limit of increasingly large circles. I don’t understand why. Can you give me some hints for that? Thanks.
2 November, 2010 at 7:19 am
Terence Tao
Intuitively, one can see the convergence by placing, for each large radius R, a circle of that radius in the plane centred at (0,R). This circle (which is given by the equation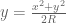
) will converge to the x-axis 
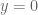in the limit as R tends to infinity.
A formalisation of this convergence is given by the notion of Gromov-Hausdorff convergence (and several other related notions of convergence would apply here too).
3 November, 2010 at 4:14 am
Ray
Dear Prof. Tao
when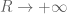 
. I can imagine a process that a circle is being pressed vertically, its major axis is getting larger and the minor axis is getting smaller at the same time. Obviously, the limit of the process is a line. However, I don’t think the process is what you wanted to discribe. Can you give me some further explanation? Thanks.
Thanks for the reply. But I can not understand the example that
3 November, 2010 at 7:31 am
Terence Tao
Here is a picture that depicts the process:
http://etc.usf.edu/clipart/42900/42929/circle-35_42929.htm
4 November, 2010 at 4:45 am
Ray
Yes. I get it. A circle of infinite radius is just a line. It can be explained by curvature. The curvature of a circle is 1/R. When
, the curvature tends to 0 everywhere. That means a straight line. Thanks for taking me new knowledge.