This is my second Milliman lecture, in which I talk about recent applications of ideas from additive combinatorics (and in particular, from the inverse Littlewood-Offord problem) to the theory of discrete random matrices.
In many areas of physics, chemistry, and computer science, one often has to study large matrices A, which for sake of discussion we shall take to be square, thus is an
matrix for some large integer n, and the
are real or complex numbers. In some cases A will be very structured (e.g. self-adjoint, upper triangular, sparse, circulant, low rank, etc.) but in other cases one expects A to be so complicated that there is no usable structure to exploit in the matrix. In such cases, one often makes the non-rigorous (but surprisingly accurate, in practice) assumption that A behaves like a random matrix, whose entries are drawn independently and identically from a single probability distribution (which could be continuous, discrete, or a combination of both). Each choice of distribution determines a different random matrix ensemble. Two particularly fundamental examples of continuous ensembles are:
- The real Gaussian random matrix ensemble, in which each
is distributed independently according to the standard normal distribution
. This ensemble has the remarkable feature of being invariant under the orthogonal group O(n); if R is a rotation or reflection matrix in O(n), and A is distributed as a real Gaussian random matrix, then RA and AR are also distributed as a real Gaussian random matrix. (This is ultimately because the product of n Gaussian measures
on
is a Gaussian measure
on
, which is manifestly rotation-invariant.)
- The complex Gaussian random matrix ensemble, in which the
are distributed according to a complex normal distribution
. This ensemble has the feature of being invariant under the unitary group U(n).
Two particularly fundamental examples of discrete ensembles are
- The Bernoulli ensemble, in which each
is distributed independently and uniformly in the set
, thus A is a random matrix of signs.
- The lazy (or sparse) Bernoulli ensemble, in which each
is independently equal to -1 or +1 with probability p/2, and equal to 0 with probability 1-p, for some fixed
, thus A is a sparse matrix of signs of expected density p.
The Bernoulli and sparse Bernoulli ensembles arise naturally in computer science and numerical analysis, as they form a simple model for simulating the effect of numerical roundoff error (or other types of digital error) on a large matrix. Continuous ensembles such as the Gaussian ensembles, in contrast, are natural models for matrices in the analog world, and in particular in physics and chemistry. [For reasons that are still somewhat mysterious, these ensembles, or more precisely their self-adjoint counterparts, also seem to be good models for various important statistics in number theory, such as the statistics of zeroes of the Riemann zeta function, but this is not the topic of my discussion here.] There are of course many other possible ensembles of interest that one could consider, but I will stick to the Gaussian and Bernoulli ensembles here for simplicity.
If A is drawn randomly from one of the above matrix ensembles, then we have a very explicit understanding of how each of the coefficients of the matrix A behaves. But in practice, we want to study more “global” properties of the matrix A which involve rather complicated interactions of all the coefficients together. For instance, we could be interested in the following (closely related) questions:
- Dynamics. Given a typical vector
, what happens to the iterates
in the limit
?
- Expansion and contraction. Given a non-zero vector x, how does the norm
of Ax compare with the norm
of x? What is the largest ratio
? The smallest ratio? The average ratio?
- Invertibility. Is the equation
solvable for every vector b? Do small fluctuations in b always cause small fluctuations in x, or can they cause large fluctuations? (In other words, is the invertibility problem stable?)
As any student of linear algebra knows, these questions can be answered satisfactorily if one knows the eigenvalues (counting multiplicity) and singular values
of the matrix A. (As the matrix A is not self-adjoint, the eigenvalues can be complex-valued even if the coefficients of A are real-valued; however, the singular values are always non-negative reals, because
is self- adjoint and positive semi-definite.) For instance:
- The largest eigenvalue magnitude
determines the maximal rate of exponential growth or decay of
(ignoring polynomial growth corrections coming from repeated eigenvalues), while the smallest eigenvalue magnitude
determines the minimal rate of exponential growth.
- The ratio
has a maximal value of
, a minimal value of
, and a root mean square value of
if the orientation of x is selected uniformly at random.
- The matrix A is invertible if and only if all eigenvalues are non-zero, or equivalently if
is positive.
- The stability of the invertibility problem is controlled by the condition number
.
So, one of the fundamental problems in the theory of random matrices is to understand how the eigenvalues and singular values of a random matrix A are distributed. (More generally, it is of interest to study the eigenvalues and singular values of A+B, where A is drawn from a standard random matrix ensemble, and B is a fixed deterministic matrix, but for simplicity we will not discuss this case here.) But how does one get a handle on these numbers?
The direct approach of working with the characteristic equation (or
) looks very unpromising; one is asking to find the roots of a large degree polynomial, most of whose coefficients depend in a hopelessly complicated way on the coefficients on A.
In the special cases of the Gaussian orthogonal and unitary ensembles, there is a massive amount of algebraic structure coming from the action of O(n) and U(n) that allows one to explicitly compute various multidimensional integrals, and this approach actually works! One gets a very explicit and useful explicit formula for the joint eigenvalue distribution (first worked out by Ginibre, I believe) this way. But for more general ensembles, such as the Bernoulli ensemble, such algebraic structure is not present, and so it is unlikely that any useful explicit formula for the joint eigenvalue distribution exists. However, one can still obtain a lot of useful information if, instead of trying to locate each eigenvalue or singular value directly, one instead tries to compute various special averages (e.g. moments) of these eigenvalues or singular values. For instance, from undergraduate linear algebra we have the fundamental formulae
and
connecting the trace and determinant of a matrix A to its eigenvalues, and more generally
(1)
and similarly for the singular values, we have
.
So, if one can easily compute traces and determinants of the matrix A (and various other matrices related to A), then one can in principle get quite a bit of control on the eigenvalues and singular values. It is also worth noting that the eigenvalues and singular values are related to each other in several ways; for instance, we have the identity
(2)
(which comes from comparing the determinants of A and ), the inequality
(3)
(which comes from looking at the ratio when x is an eigenvector), and the inequality
(4)
(which is easiest to see by using QR (or KAN) decomposition of the eigenvector matrix to rotate the matrix A to be upper triangular, and then computing the trace of ).
Let’s give some simple examples of this approach. If we take A to be the Gaussian or Bernoulli ensemble, then the trace of A has expectation zero, and so we know that the sum has expectation zero also. (Actually, this is easy to see for symmetry reasons: A has the same distribution as -A, and so the distribution of eigenvalues also has a symmetry around the origin.) The trace of
, by contrast, is the sum of the squares of all the matrix coefficients, and will be close to
(for the Bernoulli ensemble, it is exactly
); thus we see that
, and so by (4) we have
. So we see that the eigenvalues and singular values should be about
on the average. By working a little harder (e.g. by playing with very high moments of
) one can show that the largest singular value is also going to be
with high probability, which then implies by (3) that all eigenvalues and singular values will be
. Unfortunately, this approach does not seem to yield much information on the least singular value, which plays a major role in the invertibility and stability of A.
It is now natural to normalise the eigenvalues and singular values of A by , and consider the distribution of the set of normalised eigenvalues
. If one plots these normalised eigenvalues numerically in the complex plane for moderately large n (e.g. n=100), one sees a remarkable distribution; the eigenvalues appear to be uniformly distributed in the unit circle
. (For small n, there is a little bit of a clustering on the real line, just because polynomials with real coefficients tend to have a couple of real zeroes, but this clustering goes away in the limit as n goes to infinity.) This phenomenon is known as the circular law; more precisely, if we let n tend to infinity, then for every sufficiently nice set R in the plane (e.g. one could take R to be a rectangle), one has
.
(Technically, this formulation is known as the strong circular law; there is also a weak circular law, which asserts that one has convergence in probability rather than almost sure convergence. But for this talk I will ignore these distinctions.)
The circular law was first proven in the case of the Gaussian unitary ensemble by Mehta in 1967, using an explicit formula for the joint distribution of the eigenvalues. But for more general ensembles, in which explicit formulae were not available, progress was more difficult. The method of moments (in which one uses (1) to compute the sums of powers of the eigenvalues) is not very useful because of the cancellations caused by the complex nature of the eigenvalues; indeed, one can show that is roughly zero for every m, which is consistent with the circular law but also does not preclude, for instance, all the eigenvalues clustering at the origin. [For random self-adjoint matrices, the moment method works quite well, leading for instance to Wigner’s semi-circular law.]
The first breakthrough was by Girko in 1984, who observed that the eigenvalue distribution could be recovered from the quantities
(5)
for complex z (this expression is known as the Stieltjes transform of the normalised eigenvalue distribution of A). To compute this quantity, Girko then used the formula (2) to relate the determinant of with the singular values of this matrix. The singular value distribution could then be computed by the moment method (note that singular values, unlike eigenvalues, are real and non-negative, and so we do not have cancellation problems). Putting this all together and doing a large number of algebraic computations, one eventually obtains (formally, at least) a proof of the circular law.
There was however a technical difficulty with the above analysis, which was that the formula (2) becomes very unstable when the least singular value is close to zero (basically because of a division by zero problem). This is not merely a technical issue but is fundamental to the general problem of controlling eigenvalues of non-self-adjoint matrices : these eigenvalues can become very unstable near a region of pseudospectrum, which can be defined as a complex number z such that the least singular value of
is small. The classic demonstration of this comes from the perturbed shift matrices
.
For sake of discussion let us take n to be even. When , this matrix is singular, with least singular value
and with all n generalised eigenvalues equal to 0. But when
becomes positive, the least singular value creeps up to
, but the n eigenvalues move rapidly away from the origin, becoming
for
. This is ultimately because the zero set of the characteristic polynomial
is very sensitive to the value of
when that parameter is close to zero.
So, in order to make the circular law argument complete, one needs to get good lower bounds on the least singular value of the random matrix A (as well as variants of this matrix, such as ). In the case of continuous (non-Gaussian) ensembles, this was first done by Bai in 1997. To illustrate the basic idea, let us look at a toy problem, to show that the least singular value of a Gaussian orthogonal matrix A is usually non-zero (i.e. A is invertible with high probability). For this, we use some linear algebra. Let
denote the rows of A, which we can view as vectors in
. Then the least singular value of A vanishes precisely when
lie on a hyperplane. This implies that one of the vectors here is a linear combination of the other n-1; by symmetry, we conclude that the probability that the least singular value vanishes is bounded by n times the probability that
(say) is a linear combination of
. But
span a hyperplane at best; and
has a continuous distribution and so has only a zero probability of lying in the hyperplane. Thus the least singular value vanishes with probability zero. It turns out that this argument is robust enough to also show that the least singular value not only avoids zero, but in fact keeps a certain distance away from it; for instance, it is not hard to show with this method that the least singular value is at least
(say) with probability
, basically because each row vector is not only not a linear combination of the other rows, but in fact keeps a certain distance away from the space spanned by the other rows, with high probability.
For discrete random matrices, one runs into a new difficulty: a row vector such as is no longer continuously distributed, and so can in fact concentrate on a hyperplane with positive probability. For instance, in the Bernoulli case, a row vector X is just a random corner of the discrete cube
. There are certain hyperplanes which X can visit quite frequently; for instance, X will have a probability 1/2 of lying in the hyperplane
. In particular, there is a probability
that all rows
lie in this hyperplane, which would cause the Bernoulli matrix A to be non-invertible. (In terms of A itself, what is going on is that there is a
chance that the first column and second column coincide, which will of course destroy invertibility.) In particular, A now has a non-zero chance of being singular. [It is in fact conjectured that the singularity probability is close to this value, or more precisely equal to
. The best known upper bound currently for this probability is
, due to Bourgain, building upon earlier work of Kahn-Komlos-Szemeredi, and Vu and myself.]
One can hope to sum the singularity probability over all hyperplanes, but there are of course infinitely many hyperplanes in . Fortunately, only a few of these will have a particularly high chance of capturing X. The problem now hinges on getting a sufficiently strong control on the number of hyperplanes which are “rich” in the sense that they have a high probability of capturing X (or equivalently, that they have a large intersection with the discrete cube
).
This is where (finally!) the additive combinatorics comes in. Let be a normal vector to a given hyperplane V. (For instance, if
, one could take
.) Then V is rich if and only if the random variable
(6)
vanishes a large proportion of the time, where are independent signs. (One can view (6) as the result of an n-step random walk, in which the
step of the walk has magnitude
.) To put it another way, if
is associated to a rich hyperplane, then there are many additive relations amongst the coefficients
. What kinds of sets of numbers have such a strong amount of structure? (This problem is known as the inverse Littlewood-Offord problem; the forward Littlewood-Offord problem concerns how often (6) vanished for a given set of numbers
.)
Well, one way that many of the sums (6) could vanish is if many of the are themselves zero; for instance, we have already seen that if
, then half of the sums (6) vanish. But this is a rather degenerate case, and it is intuitively obvious that the more non-zero terms one has in the random walk, the less likely it is that the sum is going to vanish. Indeed, there is an observation of Erdős (a quick application of Sperner’s theorem) that if k of the coefficients
are non-zero,then (6) can only vanish at most
of the time. This bound is sharp; if, for instance,
and
, then the theory of random walks tells us that (6) is distributed in a roughly Gaussian and discrete fashion around the origin with standard deviation
, and so (6) should vanish about
of the time (and one can check this easily enough using Stirling’s formula). [In fact, this case is essentially the exact optimum, as follows from Erdős’ argument.]
So, now suppose that all the are non-zero. Then Erdős’ result tells us that (6) vanishes at most
of the time. But in most cases one can do a lot better; if, for instance, the
are linearly independent over the rationals, then (6) in fact never vanishes at all. It turns out that by intensively using the tools from additive combinatorics (including Fourier analysis and the geometry of numbers) one can obtain a satisfactory classification of the vectors
for which (6) has a high chance of vanishing; the precise description is technical, but basically in order for (6) to equal zero often, most of the coordinates of v must lie inside an generalised arithmetic progression of reasonably small size and dimension. Using such facts, it is possible to get good bounds on the singularity probability and on the least singular value of random discrete matrices such as Bernoulli matrices, leading in particular to the circular law for such discrete matrices (various formulations of this law have been recently obtained by Götze-Tikhomirov, Pan-Zhou, and Van and myself). [To get the best bounds on the singularity probability, one uses a slightly different argument, using Fourier analysis and additive combinatorics to compare the vanishing probability of a random walk with that of a lazy random walk, thus creating a relationship between the singularity of Bernoulli matrices and sparse Bernoulli matrices; see for instance my paper with Van on this topic.]
This theory for understanding singularity behaviour of discrete random matrices promises to have applications to some other areas of mathematics as well. For instance, the subject of smoothed analysis, in which the introduction of random noise to various numerical algorithms (such as the simplex method) increases the stability of the algorithm, can use this theory to extend the theoretical results in that subject from continuous noise models to discrete noise models (such as those created by roundoff error).
[Update, Dec 6: Terminology and typos corrected.]

15 comments
Comments feed for this article
6 December, 2007 at 6:40 am
Mark Meckes
This is a very nice talk. A correction about terminology: the terms Gaussian Orthogonal Ensemble and Gaussian Unitary Ensemble do not refer to the ensembles you defined above, but rather to their symmetric and Hermitian counterparts, respectively. In the GOE for instance, are independent for
are independent for 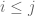 ;
;  are
are 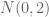 ;
;  are
are 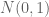 for
for 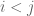 . Alternatively, if
. Alternatively, if  is the ensemble you defined with all independent
is the ensemble you defined with all independent 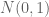 entries, then
entries, then 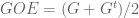 (up to the choice of normalization). The random matrix
(up to the choice of normalization). The random matrix  you defined is typically called simply a Gaussian random matrix.
you defined is typically called simply a Gaussian random matrix.
The way I prefer to think of these ensembles is that the distribution of is the standard (up to normalization) Gaussian measure on the space of real
is the standard (up to normalization) Gaussian measure on the space of real  matrices equipped with the Hilbert-Schmidt inner product, whereas the distribution of the GOE is the standard Gaussian measure on the subspace of real symmetric matrices. A similar remark holds for the complex counterpart of
matrices equipped with the Hilbert-Schmidt inner product, whereas the distribution of the GOE is the standard Gaussian measure on the subspace of real symmetric matrices. A similar remark holds for the complex counterpart of  and the GUE.
and the GUE.
The GOE/GUE as standardly defined are not invariant under multiplication by orthogonal/unitary matrices, but are invariant under conjugation by orthogonal/unitary matrices. There is a large literature on so-called orthogonal and unitary ensembles of random matrices, which generalize the GOE/GUE. These ensembles consist of real symmetric or Hermitian random matrices with dependent entries, which are invariant under orthogonal or unitary conjugation.
6 December, 2007 at 8:33 am
Terence Tao
Thanks for the corrections and comments!
6 December, 2007 at 8:58 am
Tom Smith
A small correction: in your “fundamental formula” for det(A-zI) you’ve got an extra “I” on the RHS, and similarly for det(AA* – zI). (I suppose one could regard this I as being the identity in R, ie 1, and hence parse the statement as correct; but it seems a bit of a stretch).
6 December, 2007 at 12:00 pm
Anonymous
Do you think methods like these could be extended to obtaining upper bounds on the probability that a given sequence of n numbers can be realized as the sequence of singular values of a random matrix? This would in particular be interesting for symmetric random matrices, as they might give bounds on probability that two random graphs are cospectral.
6 December, 2007 at 4:01 pm
Top Posts « WordPress.com
[…] Milliman Lecture II: Additive combinatorics and random matrices This is my second Milliman lecture, in which I talk about recent applications of ideas from additive combinatorics (and […] […]
6 December, 2007 at 10:26 pm
558
Can anyone say a little bit more about the statement below. I’m not sure how to show it.
it is not hard to show with this method that the least singular value is at least 1/n^2 (say) with probability 1-o(1), basically because each row vector is not only not a linear combination of the other rows, but in fact keeps a certain distance away from the space spanned by the other rows, with high probability.
6 December, 2007 at 11:30 pm
Terence Tao
Dear Tom: thanks for the correction!
Dear Anonymous: For continuous ensembles, it is likely that the joint distribution of eigenvalues or singular values is also continuous (though this is not entirely trivial to show), and so any given n-tuple would appear with probability 0. For discrete ensembles, the question is likely to be quite tricky. A related problem, which Van and I have thought about on occasion, is to get some non-trivial bound on how often the determinant of a Bernoulli matrix can equal some fixed non-zero value. (We understand the event where the determinant vanishes pretty well, but I can’t tell you too much about how often, say, det(A) is equal to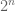 .)
.)
Dear 558: The other n-1 rows lie in a hyperplane, which have some unit normal vector w. Now, the distance from
lie in a hyperplane, which have some unit normal vector w. Now, the distance from  to the hyperplane is
to the hyperplane is 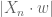 . Since the coefficients of
. Since the coefficients of  are Gaussian and independent, one can easily see that
are Gaussian and independent, one can easily see that  is also Gaussian (with a variance of n) and the claim follows. Note that if there are some linear dependencies amongst the
is also Gaussian (with a variance of n) and the claim follows. Note that if there are some linear dependencies amongst the  then the hyperplane will not be unique, but this is not a problem; the distance from
then the hyperplane will not be unique, but this is not a problem; the distance from  to the hyperplane still serves as a lower bound for the distance from
to the hyperplane still serves as a lower bound for the distance from  to the true span of the
to the true span of the  .
.
7 December, 2007 at 4:57 am
Paul Leopardi
Hi Terry,
Thanks for your lectures. The Bernoulli ensemble strongly reminds me of the Hadamard conjecture.
http://en.wikipedia.org/wiki/Hadamard_matrix
This is because the Hadamard conjecture asks about the maximum determinant of a square (-1,1) matrix of a given size, whereas the Bernoulli ensemble focuses your attention on probability distributions based on the set of all (-1,1) matrices of a given size.
I participated in Nick Witte’s AMSI Summer School course on random matrices in 2003. Since then I have been thinking on and off about a problem involving the reproducing kernel Gram matrices associated with polynomial interpolation on the sphere.
In [1] Womersley and Sloan define the Gram matrix G, which is real, symmetric and positive semi-definite, and examine the interpolation properties of sets of points on the sphere which maximize the determinant of G (“extremal fundamental systems”). In [2] Sloan and Womersley examine the quadrature properties of extremal fundamental systems.
What I’ve been thinking about in a vague way is: given (n+1)^2 points uniformly distributed on the 2-sphere, what is the distribution of G, and in what way can this be treated as an ensemble of random matrices? In particular, what can be said about the resulting distributions of eigenvalues, singular values, and determinants? What knowledge of the distribution is needed to obtain knowledge of the extremal values and vice-versa?
[1] Robert S. Womersley and Ian H. Sloan, How Good can Polynomial Interpolation on the Sphere be?, Advances in Computational Mathematics 14 (2001) 195-226.
[2] Ian H. Sloan and Robert S. Womersley, Extremal systems of points and numerical integration on the Sphere, Advances in Computational Mathematics 21 (2004) 102-125.
7 December, 2007 at 6:13 am
Mark Meckes
Regarding Terry’s response to Anonymous’s question: as Terry discussed, the invariance properties of Gaussian random matrices allow one to do quite a lot. In particular, whereas the distribution of the determinant of the Bernoulli ensemble is difficult to understand, the distribution of the determinant of a Gaussian random matrix can be determined exactly. (And for a fixed , not just asymptotically!) It turns out to be a product of independent chi-square random variables with different degrees of freedom.
, not just asymptotically!) It turns out to be a product of independent chi-square random variables with different degrees of freedom.
It’s not clear to me, however, whether it’s appropriate here to wave the magic wand of “universality” and use this result to make any conjectures about the determinant of the Bernoulli ensemble.
7 December, 2007 at 7:02 am
van vu
Dear Mark,
YEs, I think there are such conjectures. We (Terry and I) can prove some sort of universality result for ESDs. On the other hand,
at a very fine scale, the universality does not hold any more.
BEst, Van
7 December, 2007 at 8:46 am
Anonymous
Dear Terry,
Thanks for the enlightening lecture. Can these ideas be extended to matrices over finite fields? Also here there is the assumption that entries are iid. Suppose we want to get rid of this assumption and make some dependence among the entries.
Lets say only certian number of 1’s can appear in any row and certain number of 1’s in any column. Does this really complicate the problem?
Thanks.
7 December, 2007 at 11:06 am
No wai
Dear Prof Tao,
One of the most bizarre phenomenon in random matrix theory is the Tracy-Widom idea that , for example, the probability density function of the largest eigenvalue distribution in the GUE should be linked to (the tau functions) of certain integrable differential equations. In a sense, the appearance of these Painleve transcendants, with their remarkable analytic properties, is precisely what gives the conjectural links to zeta statistics.
Integrability provides perhaps the ultimate example of “structure” in nonlinear differential equations. On the other hand, your examples in this lecture are clearly using the “pseudostructure” methods of additive combinatorics.
This prompts the question: what is the natural “pseudostructured” equivalent of integrable differential equations?
8 December, 2007 at 3:36 pm
Terence Tao
Dear Paul,
It seems that information about the average case distribution of the determinant does not reveal too much information about the extreme case of the determinant, which is what is needed for Hadamard’s conjecture. For instance, Turan showed that the standard deviation of the determinant of a random Bernoulli matrix is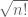 , which is significantly less than the value
, which is significantly less than the value  of the determinant of a Hadamard matrix. So this tells you (by Chebyshev’s inequality) that Hadamard matrices are only a small fraction of the set of all Bernoulli matrices, but doesn’t shed much light as to whether they exist at all.
of the determinant of a Hadamard matrix. So this tells you (by Chebyshev’s inequality) that Hadamard matrices are only a small fraction of the set of all Bernoulli matrices, but doesn’t shed much light as to whether they exist at all.
Dear anonymous: there are some results for the singularity of random Bernoulli matrices over finite fields, see e.g. this paper of Kahn and Komlos:
http://www.ams.org/mathscinet-getitem?mr=1833067
The methods are slightly different, though.
Dear No wai: I would say that the defining characteristic of structure is the presence of a group action that is large enough (or “transitive” enough) to completely determine the object being studied. For instance, with completely integrable systems it is the action of the maximal torus that can be viewed as conferring the structure. I guess one could call Hamiltonian systems that have a finite number of conservation laws but are not completely integrable to be “pseudostructured”, but it is not clear the extent to which this perspective is useful.
20 December, 2007 at 6:24 am
B.G
An interesting and accessible talk which makes me brainstorm for applications in my own field, that of time series prediction.
When studying a time-series where the time-evolution is approximated as (A + B) x_n = x_(n+1) where A is assumed to have gaussian elements, it might be useful to sample stretches of it to determine the parameters for the gaussian distribution and the eigenvalues, to get probabilities for future behaviour. (a runaway process for instance). I’m assuming that the process is non-stationary so that this sampling would have to be done on recent data.
But knowing only x_1,…x_k, does one run into the problem of invertibility stability? If it’s gaussian I should already know that the eigenvalues are O(sqrt(n)) but I would also need a test to determine if A really IS gaussian.
Can such a test be done without the invertibility stability creating trouble and are there special results or considerations when dealing with a time series?
2 February, 2019 at 10:37 am
Konstantin Tikhomrov: The Probability that a Bernoulli Matrix is Singular | Combinatorics and more
[…] are related posts on Tao’s blog What’s New. A post on Tao’s Milliman’s lecture on the additive combinatorics and random matrices; On the permamnent of random Bernoulli […]