I’ve just uploaded to the arXiv the paper “Global existence and uniqueness results for weak solutions of the focusing mass-critical non-linear Schrödinger equation“, submitted to Analysis & PDE. This paper is concerned with solutions to the focusing mass-critical NLS equation
, (1)
where the only regularity we assume on the solution is that the mass is finite and locally bounded in time. (For sufficiently strong notions of solution, the mass is in fact conserved, but part of the point with this paper is that mass conservation breaks down when the solution becomes too weak.) Note that the mass is dimensionless (i.e. scale-invariant) with respect to the natural scale invariance
for this equation. For various technical reasons I work in high dimensions
(this in particular allows the nonlinearity in (1) to be locally integrable in space).
In the classical (smooth) category, there is no ambiguity as to what it means for a function u to “solve” an equation such as (1); but once one is in a low regularity class (such as the class of finite mass solutions), there are several competing notions of solution, in particular the notions of a strong solution and a weak solution. To oversimplify a bit, both strong and weak solutions solve (1) in a distributional sense, but strong solutions are also continuous in time (in the space of functions of finite mass). A canonical example here is given by the pseudoconformally transformed soliton blowup solution
(2)
to (1), where Q is a solution to the ground state equation . This solution is a strong solution on (say) the time interval
, but cannot be continued as a strong solution beyond time zero due to the discontinuity at t=0. Nevertheless, it can be continued as a weak solution by extending by zero at t=0 and at
(or alternatively, one could extend for
using (2); thus there is no uniqueness for the initial value problem in the weak solution class. Note this example also shows that weak solutions need not conserve mass; all the mass in (1) concentrates into the spatial origin as
and disappears in the limit t=0).
There is a slightly stronger notion than a strong solution, which I call a Strichartz-class solution, in which one adds an additional regularity assumption . This assumption is natural from the point of view of Strichartz estimates, which are a major tool in the analysis of such equations.
There is a vast theory for the initial value problem for these sorts of equations, but basically one has the following situation: in the category of Strichartz class solutions, one has local existence and uniqueness, but not global existence (as the example (2) already shows); at the other extreme, in the category of weak solutions, one has global existence, but not uniqueness (as (2) again shows).
(This contrast between strong and weak solutions shows up in many other PDE as well. For instance, global existence of smooth solutions to the Navier-Stokes equation is one of the Clay Millennium problems that I have blogged about before, but global existence of weak solutions is quite easy with today’s technology and was first done by Leray back in 1933.)
In this paper, I introduce a new solution class, which I call the semi-Strichartz class; rather than being continuous in time, it varies right-continuously (in both the mass space and the Strichartz space) in time in the future of the initial time , and left-continuously in the past of
. With this tweak of the definition, it turns out that one has both global existence and uniqueness in this class. (For instance, if one started with the initial data u(-1) given by (2) at time t=-1, the unique global semi-Strichartz solution from this initial data would be given by (2) for negative times and by zero for non-negative times.) This notion of solution is analogous (but much, much simpler than) the notion of Ricci flow with surgery used by Hamilton and Perelman; basically, every time a singularity develops, the semi-Strichartz solution removes the portion of mass that was becoming discontinuous, leaving only the non-singular portion of the solution to continue onwards in time.
There are a number of other auxiliary results. For instance, I show that the mass in the semi-Strichartz class is conserved except at a finite number of “surgery times”, in which the mass drops by at least a fixed amount; in the spherically symmetric case, the mass must drop by at least the mass M(Q) of the ground state; this is consistent with the general philosophy of “quantisation of mass” for these equations. Outside of the surgery class, one has a Strichartz class solution. These results are proven by minor variations of the standard Strichartz theory (and in the spherically symmetric case, also use a global well-posedness result for masses below M(Q) of myself, Visan, and Zhang).
When I work in higher dimensions and assume spherical symmetry, I can use a decomposition of spherically symmetric waves into inward and outward components (that I used an earlier paper on NLS, as well as in a paper with Killip and Visan), there are some further results available. First of all, one can show that the notions of strong solution and Strichartz class solution are equivalent, and that weak solutions of sufficiently small mass are automatically strong. In particular, strong solutions are unique in this category (this type of result is known as unconditional uniqueness in the literature). Also, a weak solution is strong precisely when its mass function is continuous, and if the mass is continous, then it is in fact constant. So one can easily read off the nature of a solution just by inspecting how the mass changes in time.

10 comments
Comments feed for this article
19 July, 2008 at 6:22 pm
Global existence and uniqueness results for weak solutions of the focusing mass-critical non-linear Schrödinger equation | Techspedia™
[…] I’ve just uploaded to the arXiv the paper “Global existence and uniqueness results for weak solutions of the focusing mass-critical non-linear Schrödinger equation“, submitted to Analysis & PDE. This paper is concerned with solutions to the focusing mass-critical NLS equation , (1) where the only regularity we assume on the solution is that the mass is finite and locally bounded in time. (For sufficiently strong notions of solution, the mass is in fact conserved, but part of the poin The Rest Of The Story at Technorati … […]
22 July, 2008 at 10:34 pm
Fabrice Planchon
Dear Terry,
concerning unconditional well-posedness (UWP), there are a few results beyond Kato’s papers in the 90’s, most notably Furioli-Terraneo and recently Tsutsumi and one of his students. See e.g.
Click to access Tsutsumi2.pdf
Of course, UWP at scaling level for the L^2 critical NLS seems totally out of reach by these methods.
On the other hand, I am not aware of anything related to weak-strong uniqueness in the context of NLS, whereas for Navier-Stokes there is quite a litterature on it (see a CRAS note by Lions-Masmoudi for a short and elegant proof); so I quite like the result in that spirit in the radial case !
23 July, 2008 at 9:53 am
Terence Tao
Dear Fabrice,
Thanks for the comments and references! I had wondered what the precise analogue of the Navier-Stokes weak-strong uniqueness results for NLS would be, but I am not sure exactly what they should be, given that uniqueness for weak solutions to NLS can break down even for zero initial data. But what the radial case seems to show is that as long as one somehow excludes a significant amount of mass from being spontaneously created or destroyed, then one has uniqueness of weak solutions (in particular, one has uniqueness when the mass is uniformly small).
24 July, 2008 at 5:16 am
Fabrice Planchon
Hey,
It will look like I am trying to lenghten your references ;-), but I recalled 2 other things which I should mention to be fair: one is again on unconditional uniqueness, a CRAS note by Keith Rogers (probably overlaps Tsutsumi, but the interesting point is that he is using off-diagonal inhomogeneous estimates to get something). The other is actually a weak-strong uniquess result by Michael Struwe (in the supercritical setting and considering smooth solutions as the strong ones). Somehow one has to add some entropy condition on the weak solution, and reversibility suggests mass conservation, I guess…
29 July, 2008 at 1:24 pm
Terence Tao
Dear Fabrice: Thanks again for the references!
In the high-dimensional radial case, one can recover uniqueness of weak solutions as long as one imposes a monotonicity condition on the mass; this follows from one of the results in my paper. I suspect this to be true in the non-radial case, but this will need a lot more analysis.
29 July, 2008 at 2:45 pm
Peter
I’m not an analyst, so this might be a dumb question, but I’ll ask it anyway. It seems like in several of your posts, a result that assumes radial symmetry is easier than the same result without the assumption of symmetry. I guess it seems obvious that symmetry in general makes things easier, but is there some more specific or informative reason this happens with some of the results you’ve discussed? Also, radial symmetry seems to be more useful than other types of symmetry, is there a reason for this?
29 July, 2008 at 7:59 pm
Terence Tao
Dear Peter,
There are several advantages to assuming spherical symmetry. One is that many equations preserve spherical symmetry: spherically symmetric initial data leads to spherically symmetric solutions. (This is ultimately due to the fact that many equations enjoy a rotation invariance symmetry, as well as uniqueness for the initial value problem.) Another is that spherically symmetric states must necessarily have zero total momentum, and centre of mass at the origin; this tends to rule out many examples of singularity formation in which the position or momentum of the solution (or of key components of the solution) escape to infinity. (There is still the problem that the wavelength of the solution could concentrate to zero in finite time.) Related to this, spherically symmetric waves with bounded energy (or bounds on other energy-like quantities) tend to decay spatially away from the spatial origin, because in order for a spherically symmetric wave to have large amplitude at a point far away from the origin, it must in fact be large on the entire sphere that contains that point, which requires a large amount of energy.
Somewhat paradoxically, one advantage of imposing spherical symmetry on the solution is that it destroys some other symmetries that might otherwise be present in the equation, notably translation symmetry and Galilean or Lorentz invariance. The point is that symmetric problems often require symmetric proofs; for instance, solving a translation-invariant PDE in a translation-invariant class of initial data is likely to require translation-invariant techniques. Breaking such a symmetry removes this requirement and (in principle) allows a much larger range of techniques to be brought to bear on the problem (e.g. weighted estimates, which are generally not translation-invariant).
Another key advantage is that spherical symmetry allows for a dimensional reduction: if one expresses physical space in polar coordinates, the angular variable tends to behave trivially for spherically symmetric solutions (pretty much by definition) and so one can often transform a PDE in many spatial dimensions to a PDE in just one spatial dimension, which is often much simpler for a variety of reasons. (For instance, wave equations in one spatial dimension have extremely simple solutions compared to those in higher dimensions.)
From a more technical viewpoint, many estimates in harmonic analysis become easier to prove and/or stronger when assuming spherical symmetry; for instance, the Sobolev embedding theorem admits some very useful weighted generalisations in the spherically symmetric case.
It is really quite fortunate in nonlinear wave equations that we have the spherically symmetric model to play with as a test case; there are quite a few examples of major problems that looked hopeless to solve directly, until someone first tackled the much simpler spherically symmetric case, thus giving both a psychological boost to solving the original problem, as well as providing valuable clues and insight as to how to proceed (or perhaps more importantly, how not to proceed) in general.
23 February, 2009 at 12:56 pm
Tim Candy
Dear Prof. Tao
I was reading through your paper “Global existence and uniqueness results for weak solutions of the focusing mass-critical non-linear Schrödinger equation” and found the definition of a semi-Strichartz solution a little strange. I think perhaps you mean instead of
instead of 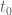 in the last line of the following on page 6,
in the last line of the following on page 6,
“…A semi-strong solution (resp. semi-Strichartz class solution) is a weak solution such that for every $\latex t \in I \cap [t_0,+∞) $ there exists
such that for every $\latex t \in I \cap [t_0,+∞) $ there exists  such that
such that  is a strong solution (resp. Strichartz class solution) when restricted to
is a strong solution (resp. Strichartz class solution) when restricted to  , and for…”
, and for…”
Since if we consider the solution (2) above then it satisfies this definition (picking ) if we either extend it to zero for
) if we either extend it to zero for  , or use (2) again in this region. Hence we dont have uniqueness.
, or use (2) again in this region. Hence we dont have uniqueness.
Tim
23 February, 2009 at 3:02 pm
Terence Tao
Dear Tim: Thanks for the correction!
6 February, 2023 at 6:02 am
Yunrui
In the proof of Thm1.18, it seems that Prop 1.11 is not used.
[This is correct – T.]