Jean-Pierre Serre (whose papers are, of course, always worth reading) recently posted a lovely lecture on the arXiv entitled “How to use finite fields for problems concerning infinite fields“. In it, he describes several ways in which algebraic statements over fields of zero characteristic, such as , can be deduced from their positive characteristic counterparts such as
, despite the fact that there is no non-trivial field homomorphism between the two types of fields. In particular finitary tools, including such basic concepts as cardinality, can now be deployed to establish infinitary results. This leads to some simple and elegant proofs of non-trivial algebraic results which are not easy to establish by other means.
One deduction of this type is based on the idea that positive characteristic fields can partially model zero characteristic fields, and proceeds like this: if a certain algebraic statement failed over (say) , then there should be a “finitary algebraic” obstruction that “witnesses” this failure over
. Because this obstruction is both finitary and algebraic, it must also be definable in some (large) finite characteristic, thus leading to a comparable failure over a finite characteristic field. Taking contrapositives, one obtains the claim.
Algebra is definitely not my own field of expertise, but it is interesting to note that similar themes have also come up in my own area of additive combinatorics (and more generally arithmetic combinatorics), because the combinatorics of addition and multiplication on finite sets is definitely of a “finitary algebraic” nature. For instance, a recent paper of Vu, Wood, and Wood establishes a finitary “Freiman-type” homomorphism from (finite subsets of) the complex numbers to large finite fields that allows them to pull back many results in arithmetic combinatorics in finite fields (e.g. the sum-product theorem) to the complex plane. (Van Vu and I also used a similar trick to control the singularity property of random sign matrices by first mapping them into finite fields in which cardinality arguments became available.) And I have a particular fondness for correspondences between finitary and infinitary mathematics; the correspondence Serre discusses is slightly different from the one I discuss for instance in here or here, although there seems to be a common theme of “compactness” (or of model theory) tying these correspondences together.
As one of his examples, Serre cites one of my own favourite results in algebra, discovered independently by Ax and by Grothendieck (and then rediscovered many times since). Here is a special case of that theorem:
Theorem 1 (Ax-Grothendieck theorem, special case) Let
be a polynomial map from a complex vector space to itself. If
is injective, then
is bijective.
The full version of the theorem allows one to replace by an algebraic variety
over any algebraically closed field, and for
to be an morphism from the algebraic variety
to itself, but for simplicity I will just discuss the above special case. This theorem is not at all obvious; it is not too difficult (see Lemma 5 below) to show that the Jacobian of
is non-degenerate, but this does not come close to solving the problem since one would then be faced with the notorious Jacobian conjecture. Also, the claim fails if “polynomial” is replaced by “holomorphic”, due to the existence of Fatou-Bieberbach domains.
In this post I would like to give the proof of Theorem 1 based on finite fields as mentioned by Serre, as well as another elegant proof of Rudin that combines algebra with some elementary complex variable methods. (There are several other proofs of this theorem and its generalisations, for instance a topological proof by Borel, which I will not discuss here.)
Update, March 8: Some corrections to the finite field proof. Thanks to Matthias Aschenbrenner also for clarifying the relationship with Tarski’s theorem and some further references.
— 1. Proof via finite fields —
The first observation is that the theorem is utterly trivial in the finite field case:
Theorem 2 (Ax-Grothendieck theorem in
) Let
be a finite field, and let
be a polynomial. If
is injective, then
is bijective.
Proof: Any injection from a finite set to itself is necessarily bijective. (The hypothesis that is a polynomial is not needed at this stage, but becomes crucial later on.)
Next, we pass from a finite field to its algebraic closure
.
Theorem 3 (Ax-Grothendieck theorem in
) Let
be a finite field, let
be its algebraic closure, and let
be a polynomial. If
is injective, then
is bijective.
Proof: Our main tool here is Hilbert’s nullstellensatz, which we interpret here as an assertion that if an algebraic problem is insoluble, then there exists a finitary algebraic obstruction that witnesses this lack of solution (see also my blog post on this topic). Specifically, suppose for contradiction that we can find a polynomial which is injective but not surjective. Injectivity of
means that the algebraic system
has no solution over the algebraically closed field ; by the nullstellensatz, this implies that for each
, there must exist an algebraic identity of the form
for some and some polynomial
that specifically witnesses this lack of solvability. Similarly, lack of surjectivity means the existence of an
such that the algebraic system
has no solution over the algebraically closed field ; by another application of the nullstellensatz, there must exist an algebraic identity of the form
for some polynomial that specifically witnesses this lack of solvability.
Fix as above, and let
be the subfield of
generated by
and the coefficients of
. Then we observe (thanks to our explicit witnesses (1), (2)) that the counterexample
descends from
to
;
is a polynomial from
to
which is injective but not surjective.
But is finitely generated, and every element of
is algebraic over the finite field
, thus
is finite. But this contradicts Theorem 2.
The complex case follows by a slight extension of the argument used to prove Theorem 3. Indeed, suppose for contradiction that there is a polynomial
which is injective but not surjective. As
is algebraically closed, we may invoke the nullstellensatz as before and find witnesses (1), (2) for some
.
Now let be the subfield of
generated by the rationals
and the coefficients
of
. Then we can descend the counterexample to
. This time,
is not finite, but we can descend it to a finite field (and obtain the desired contradiction) by a number of methods. One approach, which is the one taken by Serre, is to quotient the ring
generated by the above coefficients by a maximal ideal, observing that this quotient is necessarily a finite field. Another is to use a general mapping theorem of Vu, Wood, and Wood. We sketch the latter approach as follows. Being finitely generated, we know that
has a finite transcendence basis
over
. Applying the primitive element theorem, we can then express
as the finite extension of
by an element
which is algebraic over
; all the coefficients
are thus rational combinations of
. By rationalising, we can ensure that the denominators of the expressions of these coefficients are integers in
; dividing
by an appropriate power of the product of these denominators we may assume that the coefficients in
all lie in the commutative ring
, which can be identified with the commutative ring
generated by formal indeterminates
, quotiented by the ideal generated by the minimal polynomial
of
; the algebraic identities (1), (2) then transfer to this ring. Now pick a large prime
, and map
to random elements of
. With high probability, the image of
(which is now in
) is non-degenerate; we can then map
to a root of this image in a finite extension of
. (In fact, by using the Chebotarev density theorem (or Frobenius density theorem), we can place
back in
for infinitely many primes
.) This descends the identities (1), (2) to this finite extension, as desired.
Remark 4 This argument can be generalised substantially; it can be used to show that any first-order sentence in the language of fields is true in all algebraically closed fields of characteristic zero if and only if it is true for all algebraically closed fields of sufficiently large characteristic. This result can be deduced from the famous result (proved by Tarski, and independently, in an equivalent formulation, by Chevalley) that the theory of algebraically closed fields (in the language of rings) admits elimination of quantifiers. See for instance Section IV.23.4 of the Princeton Companion to Mathematics. There are also analogues for real closed fields, starting with the paper of Bialynicki-Birula and Rosenlicht, with a general result established by Kurdyka. Ax-Grothendieck type properties in other categories have been studied by Gromov, who calls this property “surjunctivity”.
— 2. Rudin’s proof —
Now we give Rudin’s proof, which does not use the nullstellensatz, instead relying on some Galois theory and the topological structure of . We first need a basic fact:
Lemma 5 Let
be an open set, and let
be an injective holomorphic map. Then the Jacobian of
is non-degenerate, i.e.
for all
.
Actually, we only need the special case of this lemma when is a polynomial.
Proof: We use an argument of Rosay. For the claim follows from Taylor expansion. Now suppose
and the claim is proven for
. Suppose for contradiction that
for some
. We claim that
in fact vanishes entirely. If not, then we can find
such that
; by permuting we may take
. We can also normalise
. Then the map
is holomorphic with non-degenerate Jacobian at
and is thus locally invertible at
. The map
is then holomorphic at
and preserves the
coordinate, and thus descends to an injective holomorphic map on a neighbourhood of the origin
, and so its Jacobian is non-degenerate by induction hypothesis, a contradiction.
We have just shown that the gradient of vanishes on the zero set
, which is an analytic variety of codimension
(if
is polynomial, it is of course an algebraic variety). Thus
is locally constant on this variety, which contradicts injectivity and we are done.
From this lemma and the inverse function theorem we have
Corollary 6 Injective holomorphic maps from
to
are open.
Now we can give Rudin’s proof. Let be an injective polynomial. We let
be the field generated by
and the coefficients of
; thus
is definable over
. Let
be the extension of
by
indeterminates
. Inside
we have the subfield
generated by
and the components of
.
We claim that is all of
. For if this were not the case, we see from Galois theory that there is a non-trivial automorphism
that fixes
; in particular, there exists a non-trivial rational (over
) combination
of
such that
. Now map
to a random complex number in
, which will almost surely be transcendental over the countable field
; this explicitly demonstrates non-injectivity of
, a contradiction.
Since , there exists a rational function
over
for each
such that
. We may of course assume that
have no common factors.
We have the polynomial identity . In particular, this implies that on the domain
(which is open by Corollary 6), the zero set of
is contained in the zero set of
. But as
and
have no common factors, this is impossible by elementary algebraic geometry; thus
is non-vanishing on
. Thus the polynomial
has no zeroes and is thus constant; we may then normalise so that
. Thus we now have
for some polynomial
, which implies that
for all
in the open set
. But
and
are both polynomials, and thus must agree on all of
. Thus
is bijective as required.
Remark 7 Note that Rudin’s proof gives the stronger statement that if a polynomial map from
to
is injective, then it is bijective and its inverse is also a polynomial.

33 comments
Comments feed for this article
7 March, 2009 at 11:01 am
fdreher
To move the problem from to the finite field
to the finite field  , you suggest a field homomorphism that maps the elements of a transcendence base to
, you suggest a field homomorphism that maps the elements of a transcendence base to  . But is it not true that a field homomorphism has to be injective?
. But is it not true that a field homomorphism has to be injective?
7 March, 2009 at 3:18 pm
Terence Tao
Ah, you’re right (one would instead need to map the basis elements to elements of high enough degree that one can still meaningfully define all the expressions being considered here, even if it is not, strictly speaking, a field homomorphism).
Actually I was silly; since we are working inside the algebraic closure of F, k is already finite, and this step is not even needed.
8 March, 2009 at 4:10 am
fdreher
As long as the problem is in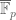 , there are no transcendent extensions. The situation is different in the complex case (if
, there are no transcendent extensions. The situation is different in the complex case (if 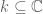 , but
, but 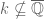 ), so this step (or something different altogether) is still needed to proof Theorem 1.
), so this step (or something different altogether) is still needed to proof Theorem 1.
8 March, 2009 at 4:34 am
Ricardo Menares
In the proof of the Ax-Grothendieck theorem for the complex numbers you give no explanation to descend from $k$ to the number field $G$ (k may very well be not a finite extension of $\mathbb{Q}$). I guess this happened because you erased the analog explanation for the positive characteristic case after fdreher’s comment (which is correct).
A way to deal with this is the following: define $k$ as the subring of $\mathbb{C}$ generated over $\mathbb{Z}$ by the coefficients of $P, Q, z_0, R$. Let $I$ be a maximal ideal of $k$. Then use the fact that $k/I$ is a finite field (Serre gives the reference Bourbaki, Algèbre commutative. Chapitre V. Entiers, p.68, cor.1 ). Equations (1) and (2) still hold in this finite field, contradicting Theorem 2.
It seems to me that you don’t even have to worry about the characteristic of the finite field being big enough, because the finitary versions of all the polynomials are well defined and (1) and (2) prevent them from being trivial.
And thanks for this great blog.
8 March, 2009 at 9:29 am
Terence Tao
Fair enough. Serre’s approach is probably the slickest, but I think I fixed the approach I had in mind (in which one “models” transcendental elements by elements in a finite field), by using some ideas of Vu, Wood, and Wood and working with the ring generated by the coefficients rather than the field. The two approaches ultimately seem to be very similar, though. (I don’t have the Bourbaki reference handy; is it easy to give a self-contained proof of the finiteness of k/I? Algebra is, unfortunately, not my strongest suit.)
8 March, 2009 at 3:59 pm
gowers
Terry, I too very much like the Ax-Grothendieck theorem, which I first came across when editing a beautiful article by David Marker on this kind of thing for the Princeton Companion. I hope you’ll forgive the plug …
8 March, 2009 at 6:06 pm
john mangual
this result has the same feel of the Hasse principle which says you solve a quadratic form over Q, by solving them over the p-adic numbers for each prime p and use the chinese remainder theorem.
Maybe your obstruction strategy is like proving that given a variety V in $\latex \mathbb{C}^n$, the set is also an affine variety. Varieties are the zero sets of polynomials and there is no reason a priori we should find polynomials which vanish precisely where g(p) is nonzero. But… if
is also an affine variety. Varieties are the zero sets of polynomials and there is no reason a priori we should find polynomials which vanish precisely where g(p) is nonzero. But… if 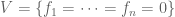 can adjoin a new variable, y, and say
can adjoin a new variable, y, and say 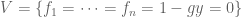 and this is a variety. (This example comes from a draft by David Cox on Toric Varieties)
and this is a variety. (This example comes from a draft by David Cox on Toric Varieties)
However this example is much crazier. Above, we showed the nonvanishing of something equals the vanishing of something else. Instead we do the same thing with existence and pulling a variety quite out of thin air.
8 March, 2009 at 6:12 pm
john mangual
Rather… is in bijection with the variety
is in bijection with the variety 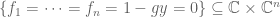 by the projection map.
by the projection map.
9 March, 2009 at 3:45 am
Ricardo Menares
Here’s a proof of the finiteness of the field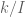 coming from algebra, using the nullstellensatz:
coming from algebra, using the nullstellensatz:
Step 1.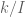 has positive characteristic: if not, then the map
has positive characteristic: if not, then the map  is injective. As
is injective. As 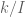 is finitely generated over
is finitely generated over 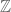 , we conclude that the rational field
, we conclude that the rational field 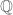 has the same property, and this is impossible (if only a finite number of rational numbers are allowed as generators, then there are only a finite number of primes that can appear in the denominators of the algebraic
has the same property, and this is impossible (if only a finite number of rational numbers are allowed as generators, then there are only a finite number of primes that can appear in the denominators of the algebraic 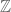 -span of such a generator set).
-span of such a generator set).
Step 2. Pass to an algebraic closure to use the nullstellensatz: let be the characteristic of
be the characteristic of 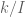 , so we have an embedding
, so we have an embedding  . Let
. Let  be an embedding in the algebraic closure compatible with the embedding
be an embedding in the algebraic closure compatible with the embedding  .
.
Write![k = \mathbb{Z}[\alpha_1, \ldots, \alpha_n]](https://s0.wp.com/latex.php?latex=k+%3D+%5Cmathbb%7BZ%7D%5B%5Calpha_1%2C+%5Cldots%2C+%5Calpha_n%5D&bg=ffffff&fg=545454&s=0&c=20201002) , where the
, where the 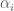 are complex numbers. We have a surjection
are complex numbers. We have a surjection ![\overline{F_p}[x_1, \ldots, x_n] \rightarrow \overline{k/I}](https://s0.wp.com/latex.php?latex=%5Coverline%7BF_p%7D%5Bx_1%2C+%5Cldots%2C+x_n%5D+%5Crightarrow+%5Coverline%7Bk%2FI%7D&bg=ffffff&fg=545454&s=0&c=20201002) defined by the rule
defined by the rule  (it’s crucial here that
(it’s crucial here that 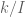 is finitely generated over
is finitely generated over 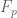 ).
).
Let $J$ be the kernell of the homomorphism above. We have![L:= \overline{F_p}[x_1, \ldots, x_n]/J](https://s0.wp.com/latex.php?latex=L%3A%3D+%5Coverline%7BF_p%7D%5Bx_1%2C+%5Cldots%2C+x_n%5D%2FJ&bg=ffffff&fg=545454&s=0&c=20201002) isomorphic to
isomorphic to  . In particular,
. In particular,  is a field, so
is a field, so  is a maximal ideal and the nullstellensatz then implies that $L$ is isomorphic to
is a maximal ideal and the nullstellensatz then implies that $L$ is isomorphic to  . Hence the
. Hence the  mod $I$ are algebraic over
mod $I$ are algebraic over 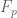 , showing the result.
, showing the result.
To compare with your approach based on Vu, Wood, and Wood, I would say you choose the finite field over which you “model” the trascendental elements by puting a non triviality condition on the model of the minimal polynomial of the primitive element you need. This allows for some effectivity, in the sense that if you know the polynomials giving equations (1) and (2) then you can devise some test to choose the prime (I think the primitive element theorem can be made effective too). On the other hand, in the algebraic approach above the choice of the finite field is determined by the choice of the maximal ideal (thus relying on the axiom of choice), and I don’t know if this can be explicitely done.
(I think the primitive element theorem can be made effective too). On the other hand, in the algebraic approach above the choice of the finite field is determined by the choice of the maximal ideal (thus relying on the axiom of choice), and I don’t know if this can be explicitely done.
9 March, 2009 at 10:23 pm
Terence Tao
Dear Ricardo: thanks for the proof, and the interesting comparison between approaches!
10 March, 2009 at 12:56 am
anon
@Ricardo Menares: “As k/I is finitely generated over \mathbb{Z}, we conclude that the rational field \mathbb{Q} has the same property”: This is true for modules over Noetherian rings, but is it also true for algebras over Noetherian rings?
10 March, 2009 at 6:02 am
anon
But one can solve it using the general Nullstellensatz in Eisenbud, Theorem 4.19 because $\mathbf{Z}$ is Jacobson by Eisenbud, Lemma 4.20.
10 March, 2009 at 9:42 am
Utpal Sarkar
Hi Ricardo,
Is there an easy argument to show that the map![\overline{\mathbb{F}_p}[x_1,\ldots,x_m]\longrightarrow\overline{k/I}](https://s0.wp.com/latex.php?latex=%5Coverline%7B%5Cmathbb%7BF%7D_p%7D%5Bx_1%2C%5Cldots%2Cx_m%5D%5Clongrightarrow%5Coverline%7Bk%2FI%7D&bg=ffffff&fg=545454&s=0&c=20201002) is surjective (this is clear for
is surjective (this is clear for ![\mathbb{F}_p[x_1,\ldots,x_m]\longrightarrow k/I](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5Bx_1%2C%5Cldots%2Cx_m%5D%5Clongrightarrow+k%2FI&bg=ffffff&fg=545454&s=0&c=20201002) )?
)?
One could alternatively reason that since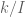 is a field that is finitely generated as an algebra over
is a field that is finitely generated as an algebra over 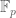 , it actually is finite over
, it actually is finite over 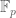 (this holds in general for field extensions).
(this holds in general for field extensions).
16 April, 2009 at 9:42 am
Tricki now live « What’s new
[…] an article on using finite fields to prove results about infinite fields which is loosely based on my own post on the topic, which is in turn based on an article of Serre.) It seems to already be growing at a reasonable […]
3 May, 2009 at 8:39 pm
Terry Hughes
Terry,
If you like this theorem, perhaps you would be interested in some partial converses to it proved by Ken McKenna a while ago. Here are two:
1) A generically surjective polynomial map of n-dimensional affine space over a finitely generated extension of Z or Z/(p)[t] is bijective with a polynomial inverse raional over the same ring (and therefore bijective on affine space of the algebraic closure).
2) A generically surjective rational map of n-dimensional affine space over a Hilbertian field is generically bijective with a rational inverse defined over the same field.
Both proofs use model theory. McKenna used (1) to show some curious facts about the distribution of integral points of a hypothetical polynomial map defined over the integers with Jacobian equal to 1 that did not satisfy the Bieberbach conjecture. He never published, but some of the material was eventually included in a paper by Lou Van den Dries in Manuscripta Mathematica some years back.
9 December, 2009 at 12:23 pm
L Spice
I’m probably being silly, but I was confused by your proof that an injective polynomial self-map on the algebraic closure of a finite field is bijective. Rather than using the full power of the Nullstellensatz, why not just observe that
on the algebraic closure of a finite field is bijective. Rather than using the full power of the Nullstellensatz, why not just observe that  is an injective polynomial map on all the finite fields containing its coefficients, hence is bijective on any such field, and then proceed by taking limits?
is an injective polynomial map on all the finite fields containing its coefficients, hence is bijective on any such field, and then proceed by taking limits?
11 December, 2009 at 1:15 pm
Terence Tao
Ah yes, that would work too :-)
24 January, 2010 at 5:05 am
Jacobian conjecture « Simple or not simple?
[…] Tao, Terence (2009-03-07). “Infinite fields, finite fields, and the Ax-Grothendieck theorem”. What’s New. […]
5 March, 2011 at 7:49 pm
Random
Minor correction: in the proof of Corollary 5, z should be mapped to a random vector in C^n, not a random complex number.
[Corrected, thanks – T.]
22 May, 2011 at 9:12 am
More On Coloring The Plane « Gödel’s Lost Letter and P=NP
[…] A powerful meta-principle that I have discussed before is the close connection between questions about complex numbers and finite fields. For a much better explanation than I could give, please see the discussion a while ago by Terence Tao here. […]
12 September, 2012 at 3:36 pm
Definable subsets over (nonstandard) finite fields, and almost quantifier elimination « What’s new
[…] first studied systematically by Ax (in the same paper where the Ax-Grothendieck theorem, discussed previously on this blog, was established), with important further contributions by Kiefe, by Fried-Sacerdote by Cherlin-van […]
20 November, 2012 at 6:31 pm
The closed graph theorem in various categories « What’s new
[…] several complex variables, it is a classical theorem (see e.g. Lemma 4 of this blog post) that a holomorphic function from a domain in to is locally injective if and only if it is a […]
23 April, 2013 at 1:32 pm
TH
Hello there,
it seems to me that you have to consider polynomial maps (i.e. n-tuples of polynomials) instead of just polynomials, as you do. Then the equations coming from the Nullstellensatz have to be adapted accordingly (which is not hard), etc.
Best regards –
26 September, 2013 at 9:36 am
Koushik Ghosh
Is there some counterexample for the following “weaker jacobian conjecture for holomorphic functions” replace polynomials with holomorphic functions and instead of asking for invertibility asking just injectivity of the holomorphic map if the jacobian does not vanish or is a non-zero constant
26 September, 2013 at 9:41 am
Koushik Ghosh
The jacobian conjecture gets reduced to asking injectivity of polynomial map from the rudin’s theorem if the jacobian is a nonzero constant.So,I am asking if the same holds if polynomials are replaced by holomorphic.
4 February, 2015 at 6:07 am
Théorème d’Ax-Grothendieck | Huhuw's Blog
[…] https://terrytao.wordpress.com/2009/03/07/infinite-fields-finite-fields-and-the-ax-grothendieck-theo… […]
11 October, 2019 at 1:37 am
Loeb
Is There an example in positive characteristic
Of a bijection polynomial map which is not
An automorphism.
3 June, 2020 at 6:38 am
Mark R.
Apologies if my understanding is a bit weak, but in your proof of Theorem 3 (Ax-Grothendieck theorem for algebraic closures of finite fields), if I’m understanding correctly, and
and  are both lists of
are both lists of  indeterminates; if so, what would
indeterminates; if so, what would  mean in that context?
mean in that context?
And kinda related, why do (1) and (2) each only involve one witness (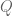 and
and  ) rather than a list of
) rather than a list of  witness polynomials? Aren’t
witness polynomials? Aren’t 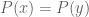 and
and  both systems of polynomial equations?
both systems of polynomial equations?
For this latter, I’m guessing the fix is quite easy (just replace them with many polynomials), but for , I can’t seem to find a fix. I’m unable to find a single polynomial equation
, I can’t seem to find a fix. I’m unable to find a single polynomial equation  that is equivalent to
that is equivalent to 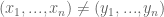 .
.
Thank you!
3 June, 2020 at 4:08 pm
Terence Tao
Oops, you are right, one needs to use a system of equations rather than one equation, involving for
for  . I’ve adjusted the text accordingly. Also the witnesses are not scalar polynomials, but themselves vector valued (
. I’ve adjusted the text accordingly. Also the witnesses are not scalar polynomials, but themselves vector valued ( take values in
take values in  ).
).
4 June, 2020 at 3:15 pm
Mark R.
Thanks for clarifying the text. And you’re right, \(Q_j\) and \(R\) are indeed vector-valued (I missed it), so it makes sense now. Thanks again. Great writeup, I learned a lot!
27 November, 2020 at 4:13 pm
Thomas
The notes here http://www.cmls.polytechnique.fr/perso/laszlo/aussois/Notes10.pdf (in french…) do elaborate on your remark 4 and also provide a much easier proof for theorem 3 (Nullstellensatz looks overly complicated, but I may have missed something).
5 June, 2022 at 11:02 pm
Teorema di Ax-Grothendieck - Wikipedia - SAPERELIBERO
[…] Terence (2009-03-07). “Campi infiniti, campi finiti e teorema di Ax-Grothendieck”. Cosa c’è di nuovo. Archiviato dall’originale l’11 marzo 2009. Recuperato […]
4 December, 2023 at 4:50 am
sfeesh
In the sentence starting with “Now let {k=Q[{\mathcal C}]} be the subfield of {{\bf C}}…” I think it should be {k = {\bf Q}[{\mathcal C}]}. Normally I wouldn’t be so pedantic, but boldface and non-boldface Q’s are being used in the same sentence.
[Corrected, thanks – T.]