The Agrawal-Kayal-Saxena (AKS) primality test, discovered in 2002, is the first provably deterministic algorithm to determine the primality of a given number with a run time which is guaranteed to be polynomial in the number of digits, thus, given a large number , the algorithm will correctly determine whether that number is prime or not in time
. (Many previous primality testing algorithms existed, but they were either probabilistic in nature, had a running time slower than polynomial, or the correctness could not be guaranteed without additional hypotheses such as GRH.)
The AKS test is of some relevance to the polymath project “Finding primes“, so I thought I would sketch the details of the test (and the proof that it works) here. (Of course, full details can be found in the original paper, which is nine pages in length and almost entirely elementary in nature.) It relies on polynomial identities that are true modulo when
is prime, but cannot hold for
non-prime as they would generate a large number of additional polynomial identities, eventually violating the factor theorem (which asserts that a polynomial identity of degree at most
can be obeyed by at most
values of the unknown).
Our starting point is Fermat’s little theorem, which asserts that
for every prime and every
. This theorem suggests an obvious primality test: to test whether a number
is prime, pick a few values of
and see whether
. (Note that
can be computed in time
for any fixed
by expressing
in binary, and repeatedly squaring
.) If the statement
fails for some
, then
would be composite. Unfortunately, the converse is not true: there exist non-prime numbers
, known as Carmichael numbers, for which
for all
coprime to
(
is the first example). So Fermat’s little theorem cannot be used, by itself, to establish primality for general
, because it is too weak to eliminate all non-prime numbers. (The situation improves though for more special types of
, such as Mersenne numbers; see my earlier post on the Lucas-Lehmer test for more discussion.)
However, there is a stronger version of Fermat’s little theorem which does eliminate all non-prime numbers. Specifically, if is prime and
is arbitrary, then one has the polynomial identity
where is an indeterminate variable. (More formally, we have the identity
in the ring
of polynomials of one variable
over the finite field
of
elements.) This identity (a manifestation of the Frobenius endomorphism) clearly implies (1) by setting
; conversely, one can easily deduce (2) from (1) by expanding out
using the binomial theorem and the observation that the binomial coefficients
are divisible by
for all
. Conversely, if
(i.e. in
) for some
coprime to
, then by comparing coefficients using the binomial theorem we see that
is divisible by
for all
. But if
is divisible by some smaller prime
, then by setting
equal to the largest power of
that divides
, one sees that
is not divisible by enough powers of
to be divisible by
, a contradiction. Thus one can use (3) (for a single value of
coprime to
) to decide whether
is prime or not.
Unfortunately, this algorithm, while deterministic, is not polynomial-time, because the polynomial has
coefficients and will therefore take at least
time to compute. However, one can speed up the process by descending to a quotient ring of
, such as
for some
. Clearly, if the identity
holds in
, then it will also hold in
, thus
The point of doing this is that (if is not too large) the left-hand side of (4) can now be computed quickly (again by expanding
in binary and performing repeated squaring), because all polynomials can be reduced to be of degree less than
, rather than being as large as
. Indeed, if
, then one can test (4) in time
.
We are not done yet, because it could happen that (4) holds but (3) fails. But we have the following key theorem:
Theorem 1 (AKS theorem) Suppose that for all
, (4) holds, and
is coprime to
. Then
is either a prime, or a power of a prime.
Of course, coprimality of and
can be quickly tested using the Euclidean algorithm, and if coprimality fails then
is of course composite. Also, it is easy to quickly test for the property that
is a power of an integer (just compute the roots
for
), and such powers are clearly composite. From all this (and (2), one soon sees that theorem gives rise to a deterministic polynomial-time test for primality. One can optimise the powers of
in the bounds for
(as is done in the original paper), but we will not do so here to keep the exposition uncluttered.
Actually, we don’t need (4) satisfied for all that many exponents to make the theorem work; just one well-chosen
will do. More precisely, we have
Theorem 2 (AKS theorem, key step) Let
be coprime to
, and such that
has order greater than
in the multiplicative group
(i.e. the residues
for
are distinct). Suppose that for all
, (4) holds, and
is coprime to
. Then
is either a prime, or a power of a prime.
To find an with the above properties we have
Lemma 3 (Existence of good
) There exists
coprime to
, such that
has order greater than
in
.
Proof: For each , the number
has at most
prime divisors (by the fundamental theorem of arithmetic). If one picks
to be the first prime not equal to any of these prime divisors, one obtains the claim. (One can use a crude version of the prime number theorem to get the upper bound on
.)
It is clear that Theorem 1 follows from Theorem 2 and Lemma 3, so it suffices now to prove Theorem 2.
Suppose for contradiction that Theorem 2 fails. Then is divisible by some smaller prime
, but is not a power of
. Since
is coprime to all numbers of size
we know that
is not of polylogarithmic size, thus we may assume
for any fixed
. As
is coprime to
, we see that
is not a multiple of
(indeed, one should view
as being much larger than
).
Let be a field extension of
by a primitive
root of unity
, thus
for some factor
(in
) of the
cyclotomic polynomial
. From the hypothesis (4), we see that
in for all
, where
. Note that
is coprime to every integer less than
, and thus
.
Meanwhile, from (2) one has
in for all such
. The two equations give
Note that the power
of a primitive
root of unity
is again a primitive
root of unity (and conversely, every primitive
root arises in this fashion) and hence we also have
in for all
.
Inspired by this, we define a key concept: a positive integer coprime to
is said to be introspective if one has
in for all
, or equivalently if
, where
is the ring homomorphism that sends
to
.
We have just shown that are all introspective;
is also trivially introspective. Furthermore, if
and
are introspective, it is not hard to see that
is also introspective. Thus we in fact have a lot of introspective integers: any number of the form
for
is introspective.
It turns out in fact that it is not possible to create so many different introspective numbers, basically the presence of so many polynomial identities in the field would eventually violate the factor theorem. To see this, let be the multiplicative group generated by the quantities
for
. Observe that
for all
. We now show that this places incompatible lower and upper bounds on
. We begin with the lower bound:
Proof: Let be a product of less than
of the quantities
(allowing repetitions), then
lies in
. Since
, there are certainly at least
ways to pick such a product. So to establish the proposition it suffices to show that all these products are distinct.
Suppose for contradiction that , where
are different products of less than
of the
. Then, for every introspective
,
as well (note that
). In particular, this shows that
are all roots of the polynomial
. But this polynomial has degree less than
, and the
are distinct by hypothesis, and we obtain the desired contradiction by the factor theorem.
Proposition 5 (Upper bound on
) Suppose that there are exactly
residue classes modulo
of the form
for
. Then
.
Proof: By the pigeonhole principle, we must have a collision
for some with
. Setting
and
, we thus see that there are two distinct introspective numbers
of size most
which are equal modulo
. (To ensure that
are distinct, we use the hypothesis that
is not a power of
.) This implies that
, and thus
for all
. But the polynomial
has degree at most
, and the claim now follows from the factor theorem.
Since has order greater than
in
, we see that the number
of residue classes
of the form
is at least
. But then
, and so Propositions 4, 5 are incompatible.
Update, Aug 12: A thorough discussion of the AKS algorithm by Andrew Granville for Bull. Amer. Math. Soc. can be found here.

31 comments
Comments feed for this article
11 August, 2009 at 12:57 pm
Henry
I like that this proof illustrates how fast (i.e. polynomial) computability fails to be analogous to general computability. If one has an “elementary” proof that a witness with some computably checkable property exists, the proof can generally be turned into a computation of that witness. (This can be made formal: if the proof can be formulated, even in a theory like full second order arithmetic, it can be converted to a computation of the witness.)
Yet, when given a composite number, the AKS primality test gives a fairly simple demonstration, in polynomial time, that there is some factor, but no way to quickly find what that factor is. Interestingly, the test does give a witness to something, and it’s the task of converting that witness into a factor which cannot be carried out quickly (in polynomial time).
11 August, 2009 at 1:06 pm
windfarmmusic
In the parenthetical at the end of the first paragraph, it seems like ‘faster’ should read ‘slower’. [Fixed, thanks – T.]
11 August, 2009 at 1:08 pm
windfarmmusic
Never mind!
11 August, 2009 at 1:37 pm
theoreticalminimum
Note: The url to the AKS paper has a backward slash after “primality” which has to be removed to get the correct url. [Fixed, thanks – T.]
11 August, 2009 at 10:50 pm
cipher3d
Thanks for this excellent explanatory post, Terry. Why is it, though, that number theoretic algorithms complexity is always done in terms of the logarithm of the number sizes? That is, the complexity of AKS on input n is polylogarithmic in n.
12 August, 2009 at 1:39 am
anoymous
I guess because you want to have a running time polynomial in the input size, i.e., the number of bits you need to write down the input. For a single number it is
12 August, 2009 at 6:55 am
Leandro
Just a minor typo: right after equation (1), it says:
“..pick a few values of and see..”. I think you mean:
“..pick a few values of $n$ and see..”.
[Actually, I meant here, but thanks for the correction. -T.]
here, but thanks for the correction. -T.]
12 August, 2009 at 7:29 am
David Speyer
“Why is it, though, that number theoretic algorithms complexity is always done in terms of the logarithm of the number sizes?”
Anonymous’s answer, that this is the size of the input, is good. One should also note that it is the efficiency of the “easy” operations: addition, multiplication, division with remainder, GCD and so forth. Since these are the building blocks of our algorithms, it makes sense to study those algorithms which are not much worse than the pieces they are built from.
12 August, 2009 at 10:43 am
Anonymous
Dear Terry,
probably, the main question that one needs to solve is the following:
suppose that we have all the set of a’s that violate (4) and thus gurantee that p is a composite and not a prime power. What do you think: can we somehow use this set to obtain a factor of p?
12 August, 2009 at 10:02 pm
Kenny Easwaran
Very nice explanation of the results! I started to get a bit confused about half way through with the big-O notations. For instance, you state Theorem 1 as:
The first sentence looks like it can be true for all while of course the second isn’t. After all, there is some constant such that (4) holds for all
while of course the second isn’t. After all, there is some constant such that (4) holds for all 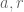 less than that constant times
less than that constant times 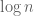 , namely 0.
, namely 0.
I suppose the right way to understand this is that the big-O expressions are all taken to introduce existential quantifiers over constants somewhere early on, with scope over the entire theorem, rather than just scope over the specific equation the big-O statement is in. And you’re also supposed to understand the scope of this quantifier with respect to various other quantifiers appropriately too. Thus, the more formal statement of Theorem 1 must say
Switching the initial existential and universal quantifiers yields a statement that is trivially true (just choose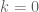 if
if  is prime or a power of a prime and
is prime or a power of a prime and  otherwise).
otherwise).
Perhaps the fact that this existential quantifier gets widest scope is implicit in the fact that it’s called a constant, but it gets more unclear when you cross sentence boundaries. Because there are other examples with the same format as the statement of Theorem 1 here where the quantifier clearly isn’t meant to have wide scope over both sentences. For instance
This doesn’t mean that there is some exponent on the polynomial that would mean cryptography is weak – rather it means that any exponent on the polynomial would work.
14 August, 2009 at 11:46 am
Jonathan Vos Post
Thank you for the clarity in showing that PRIME is in P. Now, is SEMIPRIME in P? By definition, a semiprime is a product of exactly two primes, not necessarily distinct. They matter because of an important class of cryptosystems, in a multibillion dollar industry. The complication: there exist specific semiprimes in the literature that have been proven to be semiprimes, without any prime factorization know. We don’t know the complexity class for prime factorization. So what is the complexity class for determining if a given integer is or is not a semiprime? Several experts in number theory and quantum computing have told me that mine is an interesting question, but probably very difficult. I mention quantum computing because SEMIPRIME might be in a qc complexity class of interest. What do you think?
6 December, 2009 at 1:30 am
Four Derandomization Problems « Combinatorics and more
[…] about primality certificate. and the AKS deterministic algorithm for primality is described in this post by Terry Tao (among other places). It was a beautiful combination of number theoretic ideas and derandomization […]
3 November, 2010 at 7:47 am
Manindra Agrawal and Carlos Gustavo (Gugu) Moreira share 2010 TWAS prize in Mathematics « Disquisitiones Mathematicae
[…] algorithm to decide primality of natural numbers (for a nice exposition on this subject see this post by Terence Tao), and the works of Gugu (Annales de l’IHP, 1996), and Gugu and J.-C. Yoccoz (Annals of Math. […]
22 February, 2011 at 12:18 pm
Ricardo Menares
Small typo: in the paragraph above (4) it should be (Z/NZ[x])/(X^r-1) instead of F_p[x]/(X^r-1)
[Corrected, thanks – T.]
27 September, 2011 at 8:58 am
amateur
Hello I think that binomial test is also suitable for factoring.
binomial test – phrase used from pdf in chapter 11
Click to access prime.pdf
Just see next links and you will understand:
1. key : -sieve of eratosthenes connected to triangles line N, and thus giving factors for that line N, for either composite number (or prime)
2-key :–sieve of eratosthenes connected to remainders of binomial coefficients in pascal triangle by modulo n. (compare triangle from video and pascal triangle in mod N)

Finally you will see that every midterm binomial coeficients, which are not divisible by N, correlate to factor of number N by its position and its value.
So bolded statement in next jpg is wrong

30 September, 2011 at 1:20 am
amateur
There is one more think that is of interest (for me). Aditional way of checking factors of explicit number N (for example 341 )is that you calculate mod 341 while building pascal triangle to line 341.
You will se that numbers 11 and 31 have midterm values that are divisble by 341 so mod 341 is 0.
Line 341 also gives interesting results

The only problem finding factors of 341 this way is that mod 341 doesnt take its full function for smaller numbers (lines) and these factors my be “fake” for 341 (see again first picture: fake factor 2,3,5,7)
3 October, 2011 at 12:45 am
amateur
“You will se that numbers 11 and 31 have midterm values that are divisible by 341 so mod 341 is 0.”
Wrongly put
“You will se that lines 11 and 31 have midterm values that are divisible by 11 or 31 in pascal triangle mod 341.
31 October, 2011 at 3:23 pm
gabriel b
this is so complex that i can’t understand anything. anyway i’ve made a simple program to find prime numbers by ‘brute force dividing’ that is pretty fast and completely foolproof, it would be good to use a program based on this AKS primality test that i see so much fuss about on the internet to compare the speed difference between this approach and my simple one.
i saw some project on sourceforge about this where you could download
the program and i did but i can’t see any working executable there, nor any indications, so maybe it isn’t ”the real thing”, anyway if someone knows about one executable implementation of this AKS method of discovering primes please respond to this question saying something because i’m going to be notified by e-mail.
25 November, 2011 at 4:25 am
Number Theory: Lecture 22 « Theorem of the week
[…] (The Higher Arithmetic) both have material on pseudoprimes and primality testing. Terry Tao has a blog post about the AKS primality test, with various links to further […]
25 November, 2011 at 8:00 am
amateur bojan vasiljevic
How to find factors of 2 almost primes?
N=a*b
We know that digit sum of N = digit sum of a * digit sum of b
digit sum arithmetic: http://www.applet-magic.com/Digitsum.htm
example: digit sum 341 = digit sum (3+4+1) = 8
= digit sum (31) * digit sum (11) =4*2=8
As it shown in the next picture if there exists such N that there is N=a*b (not including that a or b might be 1 and N) than a remainder of mod N with the respect to its position equals N
see picture and last line of pascal triangle in mod 341 where cell of value 31 is showed in 11s position. 31*11=431

so the algorithm for finding factors is very similiar to aks
We have mod N. Diferrence here is that aditional mod (in aks is mod (x to the power of r) -1 ) is mod 9 (digit sum equivalence). So binomial quoeficent in mod N and then (mod N * position) mod 9
And at last we check those cells with the respect of their position.
Example
For 341 we check all the cells where (value*position) mod 9=8 ( because digit sum(341)=8)
25 November, 2011 at 3:27 pm
amateur bv
Here is the case picture for number 341 where pascal triangle is in mod 341, so we look at line 341 all cells where (cell value * cell position) mod 9 = 8.
25 November, 2011 at 5:05 pm
bv
Now im interested in digt sum for binomial coefficients…..
29 February, 2012 at 2:15 pm
amateur bv
An Algorithm For Factoring Integers that uses method very similar to AKS.
They say asymptotic computational complexity of their method is unknown!?…..
http://www.google.si/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0CBsQFjAA&url=http%3A%2F%2Feprint.iacr.org%2F2012%2F097.pdf&ei=laFOT77KLIresgbXh7C7Dw&usg=AFQjCNGIlesJ5E6NVf3Bu2wyOYErxB-lAA
An Algorithm For Factoring Integers
Yingpu Deng and Yanbin Pan
29 November, 2013 at 4:04 am
Number Theory: Lecture 22 | Theorem of the week
[…] (The Higher Arithmetic) both have material on pseudoprimes and primality testing. Terry Tao has a blog post about the AKS primality test, with various links to further reading. Andrew Granville wrote an […]
19 September, 2016 at 12:51 pm
Blog 2 – Algorithms – Site Title
[…] Tao, Terence. “The AKS Primality Test.” Whtats New. WordPress, 23 Feb. 2011. Web. 19 Sept. 2016. https://terrytao.wordpress.com/2009/08/11/the-aks-primality-test/ […]
14 November, 2016 at 6:23 pm
Blog 6-Mathematics and Computer Science – Site Title
[…] Tao, Terence. “The AKS Primality Test.” Whtats New. WordPress, 23 Feb. 2011. Web. 19 Sept. 2016. https://terrytao.wordpress.com/2009/08/11/the-aks-primality-test/ […]
7 April, 2020 at 7:48 am
anonowski
“[…] where {\phi_m: F \rightarrow F} is the ring homomorphism that sends {X} to {X^m}.”
How do we know that this gives a well defined ring homomorphism?
7 April, 2020 at 11:57 am
Terence Tao
Ah, one needs to specify that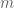 is coprime to
is coprime to  , so that
, so that 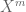 is also a primitive
is also a primitive 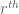 root of unity. I’ve added this to the post.
root of unity. I’ve added this to the post.
20 April, 2020 at 4:06 pm
Anonymous
Can we tell primality of (x+1)(x+2)-x when x is an integer?
12 February, 2022 at 10:44 am
Gautam Tripathi
Regarding this comment…
“But if {n} is divisible by some smaller prime {p}, then by setting {i} equal to the largest power of {p} that divides {n}, one sees that {\binom{n}{i}} is not divisible by enough powers of {p} to be divisible by {n}, a contradiction.”
Isn’t setting {i} to any prime factor of {n} sufficient to show that {\binom{n}{i}} is not divisible by {n}?
20 November, 2023 at 1:51 am
Anonymous
I think so too, since is nonzero modulo
is nonzero modulo  : if you set
: if you set  equal to
equal to 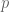 , then the binomial fraction
, then the binomial fraction  is divisible by at most
is divisible by at most  , where
, where 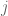 is the largest exponent of
is the largest exponent of 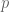 in the factorisation of
in the factorisation of 