For sake of concreteness we will work here over the complex numbers , although most of this discussion is valid for arbitrary algebraically closed fields (but some care needs to be taken in characteristic
, as always, particularly when defining the orthogonal and symplectic groups). Then one has the following four infinite families of classical Lie groups for
:
- (Type
) The special linear group
of volume-preserving linear maps
.
- (Type
) The special orthogonal group
of (orientation preserving) linear maps
preserving a non-degenerate symmetric form
, such as the standard symmetric form
(this is the complexification of the more familiar real special orthogonal group
).
- (Type
) The symplectic group
of linear maps
preserving a non-degenerate antisymmetric form
, such as the standard symplectic form
- (Type
) The special orthogonal group
of (orientation preserving) linear maps
preserving a non-degenerate symmetric form
(such as the standard symmetric form).
For this post I will abuse notation somewhat and identify with
,
with
, etc., although it is more accurate to say that
is a Lie group of type
, etc., as there are other forms of the Lie algebras associated to
over various fields. Over a non-algebraically closed field, such as
, the list of Lie groups associated with a given type can in fact get quite complicated; see for instance this list. One can also view the double covers
and
of
,
(i.e. the spin groups) as being of type
respectively; however, I find the spin groups less intuitive to work with than the orthogonal groups and will therefore focus more on the orthogonal model.
The reason for this subscripting is that each of the classical groups has rank
, i.e. the dimension of any maximal connected abelian subgroup of simultaneously diagonalisable elements (also known as a Cartan subgroup) is
. For instance:
- (Type
) In
, one Cartan subgroup is the diagonal matrices in
, which has dimension
.
- (Type
) In
, all Cartan subgroups are isomorphic to
, which has dimension
.
- (Type
) In
, all Cartan subgroups are isomorphic to
, which has dimension
.
- (Type
) in
, all Cartan subgroups are isomorphic to
, which has dimension
.
(This same convention also underlies the notation for the exceptional simple Lie groups , which we will not discuss further here.)
With two exceptions, the classical Lie groups are all simple, i.e. their Lie algebras are non-abelian and not expressible as the direct sum of smaller Lie algebras. The two exceptions are
, which is abelian (isomorphic to
, in fact) and thus not considered simple, and
, which turns out to “essentially” split as
, in the sense that the former group is double covered by the latter (and in particular, there is an isogeny from the latter to the former, and the Lie algebras are isomorphic).
The adjoint action of a Cartan subgroup of a Lie group on the Lie algebra
splits that algebra into weight spaces; in the case of a simple Lie group, the associated weights are organised by a Dynkin diagram. The Dynkin diagrams for
are of course well known, and can be found for instance here.
For small , some of these Dynkin diagrams are isomorphic; this is a classic instance of the tongue-in-cheek strong law of small numbers, though in this case “strong law of small diagrams” would be more appropriate. These accidental isomorphisms then give rise to the exceptional isomorphisms between Lie algebras (and thence to exceptional isogenies between Lie groups). Excluding those isomorphisms involving the exceptional Lie algebras
for
, these isomorphisms are
-
;
-
;
-
;
-
.
There is also a pair of exceptional isomorphisms from (the form of)
to itself, a phenomenon known as triality.
These isomorphisms are most easily seen via algebraic and combinatorial tools, such as an inspection of the Dynkin diagrams (see e.g. this Wikipedia image). However, the isomorphisms listed above can also be seen by more “geometric” means, using the basic representations of the classical Lie groups on their natural vector spaces ( for
respectively) and combinations thereof (such as exterior powers). (However, I don’t know of a simple way to interpret triality geometrically; the descriptions I have seen tend to involve some algebraic manipulation of the octonions or of a Clifford algebra, in a manner that tended to obscure the geometry somewhat.) These isomorphisms are quite standard (I found them, for instance, in this book of Procesi), but it was instructive for me to work through them (as I have only recently needed to start studying algebraic group theory in earnest), and I am recording them here in case anyone else is interested.
— 1. —
This is the simplest correspondence. is the group of transformations
that preserve the volume form;
is the group of transformations
that preserve the symplectic form. But in two dimensions, the volume form and the symplectic form are the same.
— 2. —
The group naturally acts on
. But it also has an obvious three-dimensional action, namely the adjoint action
on the Lie algebra
of
complex matrices of trace zero. This action preserves the Killing form
due to the cyclic nature of the trace. The Killing form is symmetric and non-degenerate (this reflects the simple nature of ), and so we see that each element of
has been mapped to an element of
thus giving a homomorphism from to
. The group
has dimension
, and
has dimension
, so
and
have the same dimension. The kernel of the map is easily seen to be the centre
of
, and so this is a double cover of
by
(thus interpreting
as the spin group
).
A slightly different interpretation of this correspondence, using quaternions, was discussed in this recent blog post.
— 3. —
The group naturally acts on
. Like
, it has an adjoint action (on the
-dimensional Lie algebra
), but this is not the action we will use for the
correspondence. Instead, we will look at the action on the
-dimensional exterior power
of
, given by the usual formula
Since , the volume form on
induces a bilinear form
on
; since
is even, this form is symmetric rather than anti-symmetric, and it is also non-degenerate. An element of
preserves the volume form and thus preserves the bilinear form, giving a map from
to
This is a homomorphism from to
. The group
has dimension
, and
has dimension
, so
and
have the same dimension. As before, the kernel is seen to be
, so this is a double cover of
by
(thus interpreting
as the spin group
).
— 4. —
This is basically a restriction of the correspondence. Namely, the group
acts on
in a manner that preserves the symplectic form
, and hence (on taking a wedge product) the volume form also. Thus
is a subgroup of
, and as discussed above, thus acts orthogonally on the six-dimensional space
. On the other hand, the symplectic form
can itself be thought of as an element of
, and is clearly fixed by all of
; thus
also stabilises the five-dimensional orthogonal complement
of
inside
. Note that
is non-degenerate (here we crucially use the fact that the characteristic is not two!) and so
is also non-degenerate. We have thus mapped
to
This is a homomorphism from to
. The group
has dimension
, while
has dimension
, so
and
have the same dimension. Once again, one can verify that the kernel is
, so this is a double cover of
by
(thus interpreting
as the spin group
).
Remark 1 In characteristic two, the above map from
to
disappears, but there is a somewhat different identification between
and
for any
in this case. Namely, in characteristic two, inside
with a non-degenerate symmetric form
, the set of null vectors (vectors
with
) forms a
-dimensional hyperplane, and the restriction of the symmetric form to that hyperplane becomes a symplectic form (which, in characteristic two, is defined to be an anti-symmetric form
with
for all
). This provides the claimed identification between
and
.
— 5. —
The group acts on
by tensor product:
Each individual factor preserves the symplectic form
on
, and so the pair
preserves the tensor product
, which is the bilinear form on
defined as
As each factor is anti-symmetric and non-degenerate, the tensor product
is symmetric and non-degenerate. Thus we have mapped
into
The group has dimension
, and
has dimension
, so
and
have the same dimension. As before, the kernel can be verified to be
, and so this is a double cover of
by
(thus interpreting
as the spin group
).
Remark 2 All of these exceptional isomorphisms can be treated algebraically in a unified manner using the machinery of Clifford algebras and spinors; however, I find the more ad hoc geometric approach given here to be easier to visualise.
Remark 3 In the above discussion, we relied heavily on matching dimensions to ensure that various homomorphisms were in fact isogenies. There are some other exceptional homomorphisms in low dimension which are not isogenies due to mismatching dimensions, but are still of interest. For instance, there is a way to embed the six-dimensional space
into the
-dimensional space
, by letting
act on
and
act on
, so that
acts on the six-dimensional tensor product
in the obvious manner; this preserves the tensor product of the symplectic form on
and the symmetric form on
, which is a non-degenerate symplectic form on
, giving the homomorphism (with the kernel once again being
). These sorts of embeddings were useful in a recent paper of Breuillard, Green, Guralnick, and myself, as they gave examples of semisimple groups that could be easily separated from other semisimple groups (such as
inside
) due to their irreducible action on various natural vector spaces (i.e. they did not stabilise any non-trivial space).

8 comments
Comments feed for this article
11 March, 2011 at 6:18 pm
Allen Knutson
You claim D_1 = C, but it’s actually C^x. [Ha! Good catch – T.]
12 March, 2011 at 12:54 am
Three Dimensional Algebraic Curves | Gaurav Happy Tiwari
[…] Exceptional isogenies between the classical Lie groups (terrytao.wordpress.com) […]
15 March, 2011 at 6:36 pm
Ben Wieland
A Cartan is not “any maximal connected abelian subgroup.” That works in a compact group, where every abelian subgroup is a subgroup of a Cartan. In a linear algebraic group there are not only diagonalizable elements, but also unipotent elements and subgroups of them. Cartans in algebraic groups are not contained in larger abelian subgroups, but there are unipotent subgroups that are not contained in them and which have much larger dimension. I think people usually define them as maximal tori, that is, as (abelian subgroups) consisting only of diagonalizable elements, but Cartan had a different definition involving self-normalization.
typos: the natural representation of A_n is C^n+1, not C^n; in the last line outside a remark, a “times” should be a “\times”
[Ah, that was a subtlety I was not aware of! Thanks for the corrections – T.]
29 March, 2011 at 1:49 pm
An erratum to “Strongly dense free subgroups of semisimple Lie groups” « What’s new
[…] that is double-covered by this group) in characteristic . This group (which has Dynkin diagram , as discussed in this previous post) has one maximal rank proper semisimple subgroup up to conjugacy, namely , which is the stabiliser […]
31 July, 2012 at 3:58 pm
Qiaochu Yuan
Sorry for the silly question, but what are you doing exactly when you do those dimension counts? You have nice homomorphisms between complex Lie groups of the same dimension with discrete kernel. These are clearly locally isomorphisms near the identity but I am not sure why it follows that they are surjective. Are you using a general fact about complex Lie groups? Complex manifolds? Varieties?
31 July, 2012 at 4:03 pm
Qiaochu Yuan
Oh, I see; it follows that the maps are open, and all of these groups are connected.
27 April, 2013 at 9:25 pm
Notes on the classification of complex Lie algebras | What's new
[…] resulting algebras are either isomorphic to other algebras on this list, or cease to be simple; see this previous post for further […]
8 November, 2013 at 10:28 am
Po Lam Yung
In the proof of the isomorphism between and
and  , the form
, the form 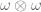 constructed there (see the second display equation in section 5) doesn’t seem to be bilinear. e.g. if one scales
constructed there (see the second display equation in section 5) doesn’t seem to be bilinear. e.g. if one scales  by 2, the right hand side of the equation mentioned above seem to scale by 4. Did I overlook something?
by 2, the right hand side of the equation mentioned above seem to scale by 4. Did I overlook something?
[Oops, I should have taken tensor product instead of direct sum here. Corrected, thanks – T.]