I’ve been meaning to return to fluids for some time now, in order to build upon my construction two years ago of a solution to an averaged Navier-Stokes equation that exhibited finite time blowup. (I recently spoke on this work in the recent conference in Princeton in honour of Sergiu Klainerman; my slides for that talk are here.)
One of the biggest deficiencies with my previous result is the fact that the averaged Navier-Stokes equation does not enjoy any good equation for the vorticity , in contrast to the true Navier-Stokes equations which, when written in vorticity-stream formulation, become
(Throughout this post we will be working in three spatial dimensions .) So one of my main near-term goals in this area is to exhibit an equation resembling Navier-Stokes as much as possible which enjoys a vorticity equation, and for which there is finite time blowup.
Heuristically, this task should be easier for the Euler equations (i.e. the zero viscosity case of Navier-Stokes) than the viscous Navier-Stokes equation, as one expects the viscosity to only make it easier for the solution to stay regular. Indeed, morally speaking, the assertion that finite time blowup solutions of Navier-Stokes exist should be roughly equivalent to the assertion that finite time blowup solutions of Euler exist which are “Type I” in the sense that all Navier-Stokes-critical and Navier-Stokes-subcritical norms of this solution go to infinity (which, as explained in the above slides, heuristically means that the effects of viscosity are negligible when compared against the nonlinear components of the equation). In vorticity-stream formulation, the Euler equations can be written as
As discussed in this previous blog post, a natural generalisation of this system of equations is the system
where is a linear operator on divergence-free vector fields that is “zeroth order” in some sense; ideally it should also be invertible, self-adjoint, and positive definite (in order to have a Hamiltonian that is comparable to the kinetic energy
). (In the previous blog post, it was observed that the surface quasi-geostrophic (SQG) equation could be embedded in a system of the form (1).) The system (1) has many features in common with the Euler equations; for instance vortex lines are transported by the velocity field
, and Kelvin’s circulation theorem is still valid.
So far, I have not been able to fully achieve this goal. However, I have the following partial result, stated somewhat informally:
Theorem 1 There is a “zeroth order” linear operator
(which, unfortunately, is not invertible, self-adjoint, or positive definite) for which the system (1) exhibits smooth solutions that blowup in finite time.
The operator constructed is not quite a zeroth-order pseudodifferential operator; it is instead merely in the “forbidden” symbol class
, and more precisely it takes the form
for some compactly supported divergence-free of mean zero with
being rescalings of
. This operator is still bounded on all
spaces
, and so is arguably still a zeroth order operator, though not as convincingly as I would like. Another, less significant, issue with the result is that the solution constructed does not have good spatial decay properties, but this is mostly for convenience and it is likely that the construction can be localised to give solutions that have reasonable decay in space. But the biggest drawback of this theorem is the fact that
is not invertible, self-adjoint, or positive definite, so in particular there is no non-negative Hamiltonian for this equation. It may be that some modification of the arguments below can fix these issues, but I have so far been unable to do so. Still, the construction does show that the circulation theorem is insufficient by itself to prevent blowup.
We sketch the proof of the above theorem as follows. We use the barrier method, introducing the time-varying hyperboloid domains
for (expressed in cylindrical coordinates
). We will select initial data
to be
for some non-negative even bump function
supported on
, normalised so that
in particular is divergence-free supported in
, with vortex lines connecting
to
. Suppose for contradiction that we have a smooth solution
to (1) with this initial data; to simplify the discussion we assume that the solution behaves well at spatial infinity (this can be justified with the choice (2) of vorticity-stream operator, but we will not do so here). Since the domains
disconnect
from
at time
, there must exist a time
which is the first time where the support of
touches the boundary of
, with
supported in
.
From (1) we see that the support of is transported by the velocity field
. Thus, at the point of contact of the support of
with the boundary of
, the inward component of the velocity field
cannot exceed the inward velocity of
. We will construct the functions
so that this is not the case, leading to the desired contradiction. (Geometrically, what is going on here is that the operator
is pinching the flow to pass through the narrow cylinder
, leading to a singularity by time
at the latest.)
First we observe from conservation of circulation, and from the fact that is supported in
, that the integrals
are constant in both space and time for . From the choice of initial data we thus have
for all and all
. On the other hand, if
is of the form (2) with
for some bump function
that only has
-components, then
is divergence-free with mean zero, and
where . We choose
to be supported in the slab
for some large constant
, and to equal a function
depending only on
on the cylinder
, normalised so that
. If
, then
passes through this cylinder, and we conclude that
Inserting ths into (2), (1) we conclude that
for some coefficients . We will not be able to control these coefficients
, but fortunately we only need to understand
on the boundary
, for which
. So, if
happens to be supported on an annulus
, then
vanishes on
if
is large enough. We then have
on the boundary of .
Let be a function of the form
where is a bump function supported on
that equals
on
. We can perform a dyadic decomposition
where
where is a bump function supported on
with
. If we then set
then one can check that for a function
that is divergence-free and mean zero, and supported on the annulus
, and
so on (where
) we have
One can manually check that the inward velocity of this vector on exceeds the inward velocity of
if
is large enough, and the claim follows.
Remark 2 The type of blowup suggested by this construction, where a unit amount of circulation is squeezed into a narrow cylinder, is of “Type II” with respect to the Navier-Stokes scaling, because Navier-Stokes-critical norms such
(or at least
) look like they stay bounded during this squeezing procedure (the velocity field is of size about
in cylinders of radius and length about
). So even if the various issues with
are repaired, it does not seem likely that this construction can be directly adapted to obtain a corresponding blowup for a Navier-Stokes type equation. To get a “Type I” blowup that is consistent with Kelvin’s circulation theorem, it seems that one needs to coil the vortex lines around a loop multiple times in order to get increased circulation in a small space. This seems possible to pull off to me – there don’t appear to be any unavoidable obstructions coming from topology, scaling, or conservation laws – but would require a more complicated construction than the one given above.

68 comments
Comments feed for this article
2 February, 2016 at 3:22 am
Anonymous
Is it possible that there is some (still unknown) obstruction for the existence of a “good” operator ?
?
2 February, 2016 at 9:08 am
Terence Tao
In principle yes, but I feel this is more a limitation of my methods than the presence of an inherent obstruction. The issue is that I do not have any usable control on the solution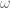 other than the conservation of circulation, which is a fairly powerful conservation law but is not fully coercive. As a consequence, I can only control a small fraction of the degrees of freedom of the dynamics – enough to control the carefully designed operator
other than the conservation of circulation, which is a fairly powerful conservation law but is not fully coercive. As a consequence, I can only control a small fraction of the degrees of freedom of the dynamics – enough to control the carefully designed operator  when applied to
when applied to  on the boundary of
on the boundary of  , but little else (for instance, I do not have any good control on the coefficients
, but little else (for instance, I do not have any good control on the coefficients  which briefly appear in the analysis). But morally one expects the solution to blowup in a specific fashion, basically like a laminar flow through
which briefly appear in the analysis). But morally one expects the solution to blowup in a specific fashion, basically like a laminar flow through  at time
at time  . If one writes down some plausible looking estimates suggested by such a flow model, then the contributions to the dynamics formed by adding terms to
. If one writes down some plausible looking estimates suggested by such a flow model, then the contributions to the dynamics formed by adding terms to  to make it invertible, positive definite, and self-adjoint (e.g. a copy of
to make it invertible, positive definite, and self-adjoint (e.g. a copy of 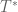 , and also a small multiple of the identity) should be negligible; similar heuristics suggest that a viscosity term could also be added. But it could be that the fluid departs radically from the laminar flow model, in particular it might prematurely develop some sort of near-singularity in which a large amount of very turbulent behaviour appears, at which point the solution inside
, and also a small multiple of the identity) should be negligible; similar heuristics suggest that a viscosity term could also be added. But it could be that the fluid departs radically from the laminar flow model, in particular it might prematurely develop some sort of near-singularity in which a large amount of very turbulent behaviour appears, at which point the solution inside  could reach an essentially arbitrary state (subject only to the energy conservation law, which is supercritical with respect to the blowup ansatz and thus increasingly useless as one approaches the putative blowup time) and so I was not able to get any usable control on the degrees of freedom not already controlled by circulation.
could reach an essentially arbitrary state (subject only to the energy conservation law, which is supercritical with respect to the blowup ansatz and thus increasingly useless as one approaches the putative blowup time) and so I was not able to get any usable control on the degrees of freedom not already controlled by circulation.
This all comes down to a basic problem when trying to rigorously establish a blowup result in PDE; paradoxically, in order to show that a solution behaves so badly as to create a singularity in finite time, one often needs to first show the solution is good in the sense that it obeys a number of nontrivial estimates, as one often needs to demonstrate that certain “error terms” in the dynamics are negligible compared to the “main terms” that one is trying to use to induce blowup. For instance, one may need to keep the solution uniformly bounded in some rescaled or renormalised coordinates in order to show that it blows up in unrescaled coordinates. There are rare cases (like the one here, or in various “virial identity” based blowup arguments) where there are no error terms in the key estimates and one can then get blowup without needing good control on all aspects of the solution; but the price one pays for this is that one does not get a good understanding of the nature of the blowup, and in particular how stable it is with respect to perturbations of the equation.
4 February, 2016 at 2:15 am
Dejan Kovacevic
Blowups in fluids are never manifested in reality, regardless of time. Unforutunatelly, asumption and mathematical formulation that fluid can be incompressible, does not have a match in Reality of Nature and as such is core cause of all difficulties and blowups in mathematics relying on such formulation.
Until that simple fact is recognized, I am afraid that lots of effort and
time might be wasted.
[See page 13 of my slides. The regularity question for Navier-Stokes is an idealised mathematical version of the physically relevant question of whether the Navier-Stokes equations are truly a good model for physical, almost incompressible fluids such as water. -T.]
7 February, 2016 at 2:48 pm
Dejan Kovacevic
Thanks for the reference to slide 13, however, I believe that it is not so much question of Navier-Stokes as a model, but of incompressible fluid condition used in NS context.
Idealized mathematical model goes beyond limits of physical reasonability as it includes expression of pure abstraction of ‘incompressible fluid’ (emphasising here that there is significant difference from ‘incompressible flow’), which is far from a ‘good enough approximation’ as almost incompressible water is unlimited number of times more compressible than non-compressible fluid. In this case, idealized model embodied in incompressible fluid is not achievable in reality and must result with non-realistic abstract results such as singularities, blowups and similar.
In any real fluid there is fluid constituting physical particle which interacts with directly neighbouring particles. Therefore, by nature of such interaction, density of fluid is not constant as fluid particle tends to ‘flow’ towards area of lower fluid density or oscillates in an limited volume of space in which density is not constant either, depending where particular fluid particle is at any point in time.
My point- we should look into source of problems, which in my opinion is incompressible fluid condition, not NS equation itself. Everybody is trying to prove or disprove NS problem statement , which includes incompressible fluid condition. However, not all questions are right questions as some questions are simply wrong, so regardless of what one tries to prove or disprove, there is no correct answer to the wrong question.
We should question question itself which I believe is wrong and which is embodied in ‘incompressible fluid’ condition.
Thanks!
Dejan
16 February, 2016 at 4:19 pm
Bill Rider
I really think Dejan is making an important and quite valid points. NS is a good model, incompressibility may not be. In other words no real fluid under turbulent motion is actually divergence free. As such we may find that solving the incompressible NS equations yields no progress on the very important problem of turbulence. For example any discussion of the Hamiltonian character of the Euler equations is clearly meaningless for real flows, which have an intrinsically dissipative character. Indeed dissipation is the essence of turbulence.
27 February, 2016 at 2:14 pm
Anonymous
Bill Rider, a couple of naive questions come to mind: 1) does turbulence appear in numerical solutions to NSE? I thought that it did. 2) Does turbulence appear in experiments with superfluids? I’m not sure. Thanks.
29 February, 2016 at 7:23 pm
Bill Rider
I’ll respond to anonymous’ questions two questions.
Turbulence only occurs the NSE equations when the viscous aspects of the equations are resolved ala DNS. It does not appear a priori in the inviscid Euler, in other words the viscous effects are essential to get the turbulent effects. Treating the Euler equations as anything akin to Hamiltonian produces nothing like turbulence. I really think this line of investigation is a complete dead end. The fact is that our knowledge of turbulence has been quite static since Kolmogorov who probably made the largest advances in the past Century through what are largely dimensional scaling arguments (-5/3 spectrum, the 2/3 and 4/5 laws).
If we are not progressing in a field its reasonable to ask whether or not our physical model is correct. The entire critique hinges on this question, does incompressible flow contain the right equations for turbulence? Incompressibility is intrinsically unphysical in several regards: thermodynamics are removed, the sound speeds are infinite and true fluid flows of any dynamic significance are not identically divergence-free, they are divergence-free asymptotically. Turbulence is a dissipative phenomena where one of the key aspects of Kolmogorov’s theory, perhaps the most profound result is the amount of dissipation in a turbulent flow asymptotically being independent of Reynolds number. The unphysical nature of incompressibility is never fully articulated in the literature, but it probably should be. Incompressibility is certainly useful in many cases especially engineering, but its derivation from compressible flow is in the adiabatic limit to second order, turbulence is a third oder effect and decisively non-adiabatic in its character.
The key to any argument here is that compressible flows produce singularities without any difficulty under any circumstance dominated inertially. We only think of shocks in the high Mach number version of fluids. If we look at the formation criteria for shocks, the mechanisms are completely independent of Mach number. The singularities will always form if the viscous forces are small compared to the inertial. Always.
Superfluids are real fluids and those experiments, real fluids are thermodynamic fluids with real sound speeds albeit with quantum effects. The trick with superfluids turbulence is getting the very small viscosity (almost vanishing we never get to absolute zero, just close) and the very large Reynolds numbers. Its just a way of achieving an idealized turbulent state experimentally.
If I look at Frisch’s book the statement that turbulence is contained in the incompressible equations is stated axiomatically, not proven. Lack of progress in turbulence theory ought to bring this axiomatic assumption in to question. Until it does I fear progress will be dismal.
1 March, 2016 at 1:11 am
Anonymous
K41 (an absolute non-compressible theory) says that the dissipation rate in turbulence is independent of Re. Why is this significant? Assuming it is true, should we find turbulence in the Euler? But this contradicts what you advocated. Incompressibility holds consistently for both NS and Euler?!
1 March, 2016 at 6:56 am
Dejan Kovacevic
In my humble opinion, and as per my previous posting, I fully agree with Bill that line of investigation is a complete dead end, however, I would not limit such conclusion just to turbulent flows. Non-physical nature of incompressible fluid and continuity hypothesis in that context I believe represent major barrier in modeling fluid dynamics corresponding to what is happening in nature.
Let’s take an example of sound propagating through fluid, or waves in general. In the essence of sound (wave) propagation is gradient of fluid density, which for incompressible fluids has to be zero, therefore model based on such strict limitation cannot really represent such important aspect of fluid reality.
Take a look at this nicely captured sound waves (within a barrel):
In the essence of those images are gradients of fluid density distribution. Using incompressible fluid model would result with perfectly pitch-black images, and could not represent that significant aspect of fluid dynamics.
I believe that continuum mechanics which does not capture aspects of physical reality embodied in characteristics of molecules and their mutual interactions, cannot represent accurately fluid dynamics which in reality has some important aspects of behavior not captured so far. However, I believe that it is possible to, in mathematically smooth fashion capture all that is important.
In my humble opinion, I would think that instead of single “Continuum Hypothesis”, principles of “Local Causality”, “Remote Causality” (ie. Gravity) and related mathematical “Continuum Model” would accurately represent fluid dynamics.
1 March, 2016 at 4:04 am
Anonymous
Why shocks in high-Ma-number flows are singularities?
1 March, 2016 at 5:00 am
Bill Rider
I’ll answer both anonymous questions:
For K41 the significance is that the dissipation independent of Re implies the presence of singularities. That is profound. We should find these singularities in Euler, but a special sort of Euler equations. There is a big difference between Euler with no viscosity and Euler with vanishing viscosity. Moreover the limit of dissipation for the dynamic Euler equation is not zero dissipation, but a finite amount of dissipation proportional to the magnitude of the large scale inertially dominated flow. This is not what the Math community is studying hence my critique. The way the community is doing this for turbulence is quite frankly baffling.
The easy one, shocks have the same invariance to the value of viscosity as turbulence modulo a constant and dimensional-temporal effects. They have the same cubic dependence on the large scale flow as K41’s 4/5 law. In other words, the dissipation rate depends only on the large scale inertial flow and not the value of viscosity. They are singular in the sense that the steepness of the gradient only appears on scales where viscous forces are important. One key difference is that the valid solutions to shocks from the inviscid compressible Euler are found in the vanishing viscosity limit. The solutions without viscosity are nonsense. Shocks produce the same nonzero limiting behavior as K41 predicts, the Euler limit is not zero dissipation, but a finite amount.
Dynamically interesting systems never approach the dynamics described by Hamiltonian descriptions, which effectively remove dissipation (and time’s arrow).
IMHO this is exactly the sort of singular behavior we should be looking for in turbulence.
1 March, 2016 at 8:33 am
Bill Rider
Dejan,
I believe the issue with sound waves is whether they are dynamically important. Incompressibility renders them irrelevant by fiat. Sound waves are essential for shock waves, and viewed as immaterial for turbulence. I think they are actually the soul of turbulence, i.e., the “dog” and vorticity is simply the “tail”. We have been almost completely focused on the side-effect of the physics instead of the actual physics itself. Sound waves and thermodynamics are intimately connected, and I think the second law has a dominant role in this discussion. Again incompressibility removes most of this by fiat.
2 March, 2016 at 12:25 am
Anonymous
Shocks are addressed in compressible flow theory. There are numerous examples where the flow is really incompressible, such as turbulence in your coffee cup, fume wake left behind your car and wind loading by tornadoes. Incompressibility must be a valid assumption in these practical scenarios as in designs and CFD simulations.
Do your shock singularities contain infinite energy? Can you explain if the answer is no.
What is this limit of vanishing viscosity? (Do you mean the Euler (zero viscosity) and the vanishing viscosity in the Navier-Stokes?) Can you quote a numerical value, say, for air/water, as your critique aims at unphysical approaches?
It is a misinterpretation that K41 predicts singularity. Frisch’s book on this issue is more or less misleading. His discussion on the drag Re-independence in bluff body flows is incomplete.
2 February, 2016 at 5:34 am
Anonymous
Just before the first double integral of omega_z there is “that he integrals”
[Corrected, thanks – T.]
2 February, 2016 at 5:35 am
Anonymous
Is the link for the slides correct? I seem to get lost.
[Corrected, thanks – T.]
2 February, 2016 at 12:24 pm
Gil Kalai
(The links for the slides still dont work…)
[Hopefully fixed for real now – T.]
3 February, 2016 at 2:24 am
Anonymous
Thank you for this post and the slides.
2 February, 2016 at 6:57 am
Anonymous
Thanks for the very interesting post! There seems to be a small typo in the introduction: one too many “assertion” in
“Indeed, morally speaking, the assertion that finite time blowup solutions of Navier-Stokes assertion”.
[Corrected, thanks – T.]
3 February, 2016 at 1:16 am
Anonymous
Can such a blowup be considered as a new type of turbulence (which also has a similar approximate self-replication behavior at many scales, but without blowup)?
3 February, 2016 at 9:37 am
Terence Tao
I view this blowup example as closer to a neck pinch (the fine scale behaviour is concentrated in a small cube, as opposed to being dispersed throughout space as is the case with turbulent flow).
4 February, 2016 at 1:54 am
Anonymous
Suppose that there is a solution for this blowup example. Is it possible (if the asymptotic behavior of this solution near the neck pinch blowup is known) to go backward(!) in time and get a good estimate for the required initial data ?
4 February, 2016 at 8:44 am
Terence Tao
I would imagine the backwards flow near the blowup solution to be so unstable as to rule out being able to derive anything useful from the initial data from the blowup asymptotics, other than what can be deduced directly from the conservation laws. This backwards evolution moves high frequencies back into low frequencies, which is a very rare type of evolution (basically the rare flows that go against the second law of thermodynamics). It would be like taking, say, a bomb exploding into fragments, and then reversing the order of time to have fragments imploding back into a bomb. This is a valid solution of the equations of Newtonian mechanics, but is incredibly unstable – any perturbation of the fragments as initial data will lead to a final state that has no resemblance to an unexploded bomb.
4 February, 2016 at 9:07 am
Anonymous
OK. but at least this argument seems to show that the required initial data is (in some sense) “rare”.
3 February, 2016 at 7:25 am
arch1
“…constant in both space and time or…” – should the “or” be a “for”?
[Corrected, thanks -T.]
3 February, 2016 at 10:10 am
Anonymous
Is there any known upper bound for the number of conservation laws (i.e. time-invariant independent functionals of the fluid state)? Is it possible that there are some unknown conservation laws which can be used ?
3 February, 2016 at 10:51 am
Terence Tao
There is some literature on attempting to classify the conservation laws that are of a certain form (e.g. arising from an infinitesimal symmetry via Noether’s theorem), see e.g. http://www.hindawi.com/journals/ijmms/1989/147865/abs/ or http://www.ams.org/mathscinet-getitem?mr=672198 . But it is difficult to rule out the possibility of a more exotic conservation law. (To give a silly example, any arbitrary function of the orbit of the Euler flow in phase space would be conserved by the flow.) Also, there may be more general a priori bounds on quantities that are not precisely conserved, but are still bounded uniformly in time. (For instance, I showed some time ago that global regularity for periodic Navier-Stokes was equivalent to the existence of an a priori bound on the H^1 norm of the solution that depended only on the initial H^1 norm.)
There have been one or two unusual conservation laws found for Euler that are not on the standard list (energy, circulation, helicity, etc.), e.g. in the recent preprint http://arxiv.org/abs/1509.05832 , but they do not look easy to exploit.
21 June, 2016 at 1:41 pm
Ravi Shankar
Hello,
In case it is helpful, I wanted to let you know that the preprint you mentioned has been updated with a new result. In addition to an a priori lower bound involving the energy (equation (58)), there is a nonexistence result on periodic solutions that follows from this conservation law.
Best,
Ravi Shankar
22 June, 2016 at 8:48 am
Terence Tao
Thanks for this. I wanted to clarify one point in your claim about nonexistence of periodic solutions to Euler – are you referring to periodic solutions in Lagrangian coordinates only, or can you also rule out periodic solutions in Eulerian coordinates also? It seems to me that one could have a solution to the Euler equations which is periodic in the latter sense but not the former – tafter some finite time T, the velocity field returns (in Eulerian coordinates) to what it was at time zero, but all the labels might have changed in the process (i.e. each particle could be in a different location from its initial position), so that the solution is not periodic in Lagrangian coordinates.
22 June, 2016 at 1:16 pm
Ravi Shankar
I only claim nonexistence in Lagrangian coordinates. I agree that a time-periodic solution in Eulerian coordinates seems conceivable. Examples with finite energy are surprisingly hard to come by though (e.g. it would not be a potential flow, u(x,t) = grad phi(x,t), since there are no nontrivial harmonic distributions phi(x,t) with L2 gradients).
3 February, 2016 at 4:01 pm
Martin
For some critical cases of nonlinear Schrödinger and wave equations, the global existence problem is solved in a probabilistic way: almost surely, w.r.t. an invariant measure, the solution to a given initial datum exists globally in time. So there is blow up, but in reality one never hits one of these solutions.
Could such or a related scenary be realistic for Navier-Stokes as well?
3 February, 2016 at 7:56 pm
Terence Tao
It’s unlikely that Navier-Stokes, being time-irreversible and non-Hamiltonian, has any non-trivial invariant measures; this seems hard to reconcile with the monotone decreasing nature of energy and of the parabolic smoothing, for instance. In fact the parabolic smoothing even makes it challenging to conceive of a quasi-invariant measure, even for the linear heat equation. But perhaps there is some other way to obtain an almost sure global existence result; that would certainly be fantastic.
The Euler equations are Hamiltonian, and one could conceivably attempt to establish an almost sure global existence result using, say, a Gibbs measure. It may be that the equation is just too nonlinear for the existing techniques for this to work, though.
3 February, 2016 at 9:12 pm
Anonymous
Hi,
Your initial vorticity omega(0) is divergence-free, so d(eta(r))/dr must be zero for EVERY (r,theta,z). But your normalisation says function eta cannot be a constant. What sort of function eta you have in mind? Thanks.
3 February, 2016 at 11:14 pm
Terence Tao
The divergence of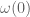 is
is 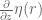 , which vanishes for any choice of
, which vanishes for any choice of 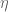 .
.
4 February, 2016 at 7:06 am
arch1
In cylindrical coordinates r is nonnegative, so why do you speak in the proof sketch of an even function eta of r supported on [-1, 1]?
4 February, 2016 at 7:31 am
Terence Tao
This is to keep the function smooth at the origin (by making all the odd order Taylor coefficients vanish at
smooth at the origin (by making all the odd order Taylor coefficients vanish at 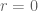 ). For instance, a function such as
). For instance, a function such as  for
for  is smooth on
is smooth on 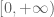 , but does not give a smooth function in cylindrical coordinates.
, but does not give a smooth function in cylindrical coordinates.
4 February, 2016 at 5:02 pm
Anonymous
Why is the function positive? May a negative be specified?
4 February, 2016 at 6:19 pm
Terence Tao
Yes; the positivity of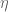 makes for a nicer picture with vortex lines only going in one direction, but the argument in fact would work with
makes for a nicer picture with vortex lines only going in one direction, but the argument in fact would work with 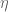 that changed sign (so long as the total circulation was still non-zero).
that changed sign (so long as the total circulation was still non-zero).
5 February, 2016 at 2:46 am
Anonymous
Is it possible that the existence of a finite blowup solution for a certain class of such problems is undecidable?
5 February, 2016 at 11:18 am
Terence Tao
As far as we know, this is a possibility. Certainly there exist PDE or even ODE which can simulate arbitrary Turing machines (see e.g. the discussion on this MathOverflow post) and from this it is not difficult to extract a PDE or ODE for which the global regularity problem is undecidable. On the other hand, Navier-Stokes global regularity on a torus for data of energy bounded by a fixed threshold E is decidable for each E; see the remarks section of this paper of mine.
5 February, 2016 at 1:25 pm
asdf
Link that should point to a MathOverflow post leads to an arxiv preprint about expander graphs. Should it point here instead?
[Link corrected, thanks – T.]
5 February, 2016 at 11:55 pm
Anonymous
One of the obvious flaws is: Kelvin’s circulation theorem has been wrongly applied. The integral over r and theta (displayed after ‘From the choice of initial data we thus have’) just states the instantaneous circulation due to (unknown) vorticity component omega_z at time t>0. You have not shown anything on the dynamics of vector omega(r,theta,z,t) for given initial data.
6 February, 2016 at 8:51 am
Terence Tao
Because of the divergence-free nature of the vorticity (allowing one to use Stokes’ theorem), one does not need complete control of the vorticity at later times to be able to use the circulation law, especially since in this situation the vorticity is confined to the region .
.
For a given choice of
of  and
and  , the circulation
, the circulation  is the circulation through a disk of the form
is the circulation through a disk of the form  for some large
for some large  (since the vorticity will vanish when
(since the vorticity will vanish when  is large enough). As time evolves, say from time
is large enough). As time evolves, say from time  to time
to time  , this disk will evolve in a largely unknown fashion; but for
, this disk will evolve in a largely unknown fashion; but for  large enough, the boundary of the disk will stay outside of the support of the vorticity, so from Stokes’ theorem the circulation of the evolved disk at time
large enough, the boundary of the disk will stay outside of the support of the vorticity, so from Stokes’ theorem the circulation of the evolved disk at time  will equal the circulation of a disk of the form
will equal the circulation of a disk of the form 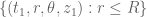 for arbitrary
for arbitrary 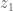 (again assuming
(again assuming  large enough). Note that the evolved disk and the new disk do not necessarily have the same boundary, but one can glue the two boundaries together by an additional surface that lies outside of
large enough). Note that the evolved disk and the new disk do not necessarily have the same boundary, but one can glue the two boundaries together by an additional surface that lies outside of  , which introduces no additional circulation.
, which introduces no additional circulation.
It is also an instructive exercise to derive the vanishing of the derivatives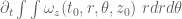 and
and  directly from the vorticity equation (1), the divergence-free nature of the vorticity, and integration by parts, without appeal to the circulation theorem.
directly from the vorticity equation (1), the divergence-free nature of the vorticity, and integration by parts, without appeal to the circulation theorem.
6 February, 2016 at 3:46 am
Anonymous
Assuming the existence of a finite time blowup solution (suggested by the above construction) with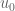 a known(!) asymptotic “main term” of the solution
a known(!) asymptotic “main term” of the solution  sufficiently near the blowup time
sufficiently near the blowup time  (i.e.
(i.e. 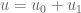 with
with  near
near  ).
).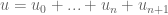 with known(!)
with known(!)  and
and 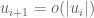 for
for 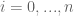 near
near  ?
? ), the relative remainder term
), the relative remainder term 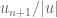 is expected to decay near
is expected to decay near  sufficiently fast to allow (via backwards evolution) the actual existence of
sufficiently fast to allow (via backwards evolution) the actual existence of 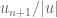 (and thereby
(and thereby  itself!) sufficiently near the blowup time
itself!) sufficiently near the blowup time  .
.
Is it possible (e.g. as done in the formal derivation of Puiseux series) to continue this formal(!) asymptotic series to
If so, then (for sufficiently large
6 February, 2016 at 9:01 am
Terence Tao
This type of construction works well for ODE-type blowup mechanisms in which the solution essentially only depends on one coordinate of spacetime (such as the time coordinate ), but for more general blowup situations (such as the neck pinch one suggested here, which is broadly like a self-similar blowup solution) one still has to do some PDE in the spatial (or rescaled spatial) directions to ensure that this series is well-behaved. For instance, for many evolution equations one can try to consider self-similar solutions, e.g. for Navier-Stokes one could consider solutions of the form
), but for more general blowup situations (such as the neck pinch one suggested here, which is broadly like a self-similar blowup solution) one still has to do some PDE in the spatial (or rescaled spatial) directions to ensure that this series is well-behaved. For instance, for many evolution equations one can try to consider self-similar solutions, e.g. for Navier-Stokes one could consider solutions of the form 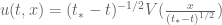 for some divergence-free
for some divergence-free  and all times
and all times  . Here, the behaviour in the time variable
. Here, the behaviour in the time variable  as it approaches the blowup time
as it approaches the blowup time  is completely explicit, but the difficulty still remains of constructing the spatial function
is completely explicit, but the difficulty still remains of constructing the spatial function  , which needs to obey a certain elliptic PDE. For instance, in this specific example it is known that there are no non-trivial bounded, finite energy
, which needs to obey a certain elliptic PDE. For instance, in this specific example it is known that there are no non-trivial bounded, finite energy  obeying this particular self-similar ansatz (thanks to the work of Necas-Ruzicka-Sverak and Tsai; this also follows from the celebrated later work of Escuriaza, Seregin, and Sverak that essentially rules out any reasonable “Type II blowup” scenario for Navier-Stokes).
obeying this particular self-similar ansatz (thanks to the work of Necas-Ruzicka-Sverak and Tsai; this also follows from the celebrated later work of Escuriaza, Seregin, and Sverak that essentially rules out any reasonable “Type II blowup” scenario for Navier-Stokes).
7 February, 2016 at 2:24 pm
Gil Kalai
How is this new blow-up result related to the program of showing blow-up by showing that the system supports computation? (In particular, do the new systems for which blow up is demonstrated support computation?)
7 February, 2016 at 6:23 pm
Terence Tao
I didn’t need to make the fluid perform any computation for this particular blowup mechanism. The reason why some sort of computation was needed in the averaged Navier-Stokes blowup was that I needed to program a delay between the transfer of energy from one scale to the next, and the transfer from that scale to the scale after that; otherwise the energy dispersed so widely that the viscosity effects dissipated the energy before it could go all the way to infinitely high frequencies to create the blowup. In the current situation there is no viscosity (and also no energy conservation law); the blowup is driven instead by the circulation conservation law and doesn’t really care if the fluid is dispersing its energy into many different frequencies. So it’s not directly advancing the blowup program I proposed from the averaged Navier-Stokes paper, but it does show that the circulation conservation law is not an insurmountable barrier to that program.
7 February, 2016 at 6:53 pm
Gil Kalai
Thanks, Terry. But can you still make the fluid perform computation in this case? While not needed for blowup in this case, it can be of some separate interest (also because in other scenarios computation is a tool toward blowup).
8 February, 2016 at 8:16 am
Terence Tao
My guess is that for any natural number , one can choose the dynamical operator
, one can choose the dynamical operator  so that it can behave (for a suitable preparation of inputs at various spatial scales) like a Turing machine that runs for time
so that it can behave (for a suitable preparation of inputs at various spatial scales) like a Turing machine that runs for time  , because it looks plausible that one can design
, because it looks plausible that one can design  at various spatial locations to simulate logic gates (and the circulation conservation law will come in handy, as it allows one to largely ignore most of the dynamics as long as the support of the vorticity is contained in a set that can be understood, much as in the blog post here). But again one is relying on the fact that one has a wide latitude to select the nonlinearity
at various spatial locations to simulate logic gates (and the circulation conservation law will come in handy, as it allows one to largely ignore most of the dynamics as long as the support of the vorticity is contained in a set that can be understood, much as in the blog post here). But again one is relying on the fact that one has a wide latitude to select the nonlinearity  (in effect “hard-wiring” the desired program into the dynamics), and in particular not requiring the equation to obey an energy or momentum conservation law (a particular convenience of not having such laws is that this allows one to violate Newton’s third law by allowing one portion of the fluid to act on another without causing a backreaction).
(in effect “hard-wiring” the desired program into the dynamics), and in particular not requiring the equation to obey an energy or momentum conservation law (a particular convenience of not having such laws is that this allows one to violate Newton’s third law by allowing one portion of the fluid to act on another without causing a backreaction).
15 February, 2016 at 2:25 pm
Anonymous
On which basis one can choose what fluid can functionally do? What computation by fluid even means? Do we have a freedom of choice what fluid can do for us? If so, why not assume that T can compute and resolve this issue and we are all done.
8 February, 2016 at 4:11 pm
Anonymous
In the question session of your talk you mention a work on Navier-Stokes with a stochastic forcing related to Kolmogorov’s law that can be interpreted as an almost sure global well-posedness result. Would you be able to provide an exact reference ? Thanks in advanced.
8 February, 2016 at 8:36 pm
Terence Tao
The result I had in mind was that of Cheskidov, Friedlander, and Shvydkoy: http://arxiv.org/abs/1112.5376
10 February, 2016 at 8:40 am
Philip
Are there characteristic fields, which are analogous to characteristic lines (which are ODE) from linear transport? The characteristic field is a PDE, and describes a level of some other equation.
10 February, 2016 at 9:24 am
Terence Tao
Probably the closest such thing is the notion of a bicharacteristic in microlocal analysis, which transports the singularities and other high frequency dynamics in linear Hamiltonian PDE. In the high frequency limit (or, after a rescaling, the semiclassical limit), a linear Hamiltonian PDE converges in a certain sense to a Hamiltonian flow (closely related to how the Schrodinger equation in quantum mechanics converges to Hamilton’s laws of motion as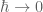 ), and the bicharacteristics are the characteristics of that latter flow in phase space.
), and the bicharacteristics are the characteristics of that latter flow in phase space.
11 February, 2016 at 12:09 pm
Fan
I know this is not the right place to advertise, but I just heard a talk (http://www.math.princeton.edu/events/seminars/ergodic-theory-statistical-mechanics/new-interactions-between-analysis-and-number) that suggests some hidden structure in the Ulam sequence : Let
: Let  . Then numerics suggest that there is an $\latex x \approx 2.57$ such that
. Then numerics suggest that there is an $\latex x \approx 2.57$ such that  . This is very unusual for a random Fourier series, which basically grows like
. This is very unusual for a random Fourier series, which basically grows like  when $\latex x$ is away from 0. Do you know any explanation related to that or can it be a suitable polymath project?
when $\latex x$ is away from 0. Do you know any explanation related to that or can it be a suitable polymath project?
11 February, 2016 at 9:13 pm
Anonymous
Why does vorticity vanish at large R? Are you saying that the other two components, omega_r and omega_theta, are always zero in the evolved disk? How do you know that the vortex lines linked to omega_z are normal to the disk for all time t>0?
12 February, 2016 at 9:49 am
Terence Tao
By the definition of , the vorticity (which is transported by the velocity field u thanks to (1), and thus propagates at finite speed) is contained inside the hyperboloid
, the vorticity (which is transported by the velocity field u thanks to (1), and thus propagates at finite speed) is contained inside the hyperboloid  for times
for times  up to
up to  , and in particular vanishes for large values of
, and in particular vanishes for large values of  .
.
The non-normal components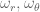 of the vorticity need not vanish (or equivalently, the vortex lines need not be orthogonal to the disk), but the circulation
of the vorticity need not vanish (or equivalently, the vortex lines need not be orthogonal to the disk), but the circulation  only depends on the normal component of the vorticity, which in this case is
only depends on the normal component of the vorticity, which in this case is 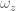 .
.
12 February, 2016 at 9:16 pm
Anonymous
Near/by your blow-up time, the velocity u cannot be finite and thus vorticity will “propagate” to infinity.
The components of o_r and o_theta must contribute to the circulation used in Kelvin’s theorem (which is not your definition).
12 February, 2016 at 9:31 pm
Terence Tao
If the solution blows up, we are done – this is precisely the conclusion of Theorem 1! The argument actually proceeds by contradiction, assuming that the solution does not blow up (which is basically equivalent to the velocity staying bounded, after dealing with some minor technical issues at spatial infinity).
There are two equivalent ways to define the circulation through a loop : one is as a line integral
: one is as a line integral  , and the other is as a surface integral
, and the other is as a surface integral 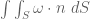 , where
, where  is any surface that has
is any surface that has  as its (oriented) boundary. The two integrals are equal by Stokes’ theorem, and so either can be used in the statement of Kelvin’s circulation theorem. In my post, I am applying Kelvin’s theorem with
as its (oriented) boundary. The two integrals are equal by Stokes’ theorem, and so either can be used in the statement of Kelvin’s circulation theorem. In my post, I am applying Kelvin’s theorem with  equal (at some initial time) to a disk of the form
equal (at some initial time) to a disk of the form  , which measures the circulation through the circle
, which measures the circulation through the circle 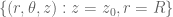 .
.
12 February, 2016 at 3:10 am
Anonymous
What is an annulus 1 << r + |z| << 1?
12 February, 2016 at 9:50 am
Terence Tao
In Euclidean coordinates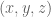 , this would be a region of the form
, this would be a region of the form  (or more precisely, a region that both contains and is contained in annuli of the form
(or more precisely, a region that both contains and is contained in annuli of the form 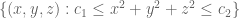 for various
for various 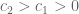 ).
).
15 February, 2016 at 1:22 am
Anonymous
Velocity u(x,t) is never indefinite despite undetermined vorticity and the loose function c(t). So the exposition of the blow-up can be rigorously sought in the realm of philosophy where finite-time singularities and the invariance principle of total vorticity must cause no contradiction, as the law of energy conservation has been overthrown by acrobatics.
15 February, 2016 at 2:04 pm
Anonymous
Absolutelly correct. Topic discussed is not in realm of physically possible. It is pure abstraction far from anything that has in common with fluids, although sounds like it.
8 March, 2016 at 5:05 am
Finite time blowup for high dimensional nonlinear wave systems with bounded smooth nonlinearity | What's new
[…] is not covered by our arguments. Nevertheless (as with previous finite-time blowup results discussed on this blog), one can view this result as a barrier to trying to prove regularity for equations such as in […]
20 April, 2016 at 5:16 am
claesjohnson
I made a comment on my blog:
http://claesjohnson.blogspot.se/2016/04/turbulent-euler-solutions-and-clay.html
Regards, Claes Johnson
20 April, 2016 at 10:22 pm
claesjohnson
To be meaningful the Clay Navier-Stokes problem needs to be reformulated to include the crucial aspect of turbulence:
http://claesjohnson.blogspot.se/2016/04/reformulation-of-clay-navier-stokes.html
I would appreciate your comment on this aspect: Is it meaningful/possible to exclude turbulence from the Clay problem?
Regards, Claes
23 May, 2016 at 4:33 pm
Erik Skjetne
Great inspiration to read your blog!
Finite time t→T blow up of the three dimensional incompressible Navier-Stokes flow velocity or vorticity may be attained by an infinite sequence, in finite time, of flow structure (e.g. neighborhood of a vorticity maximum) volume V contractions to a singularity with almost no leakage of kinetic energy in the process. Volume-contractions cannot be material, since the fluid is incompressible.
However, blow up of vorticity by vortex stretching implies that maximum and minimum eigenvalues of the fluid rate of strain tensor S split into ± ∞ (eigenvalues sum to zero by mass balance); indeed an extreme anisotropic fluid deformation. In the inertia dominated limit of the Navier-Stokes vorticity equation (the first equation above), the vorticity vector deforms as a small material fluid vector, and as a result the fluid deformation carries over to the deformation of the vorticity flow structure.
In the inertia-dominated limit (Euler eq.), the vorticity flow structure itself may deform exactly as the fluid and become incompressible! If so, the flow structure cannot reach a volume singularity and this would provide a universal kinematic barrier for blowup the Navier-Stokes equation.
What do you think about the reasoning above, any clear flaws?
23 June, 2016 at 3:14 am
Anonymous
What is known about the possibility of real analytic blowup solutions?
29 June, 2016 at 6:45 am
Finite time blowup for Lagrangian modifications of the three-dimensional Euler equation | What's new
[…] presented (for three different choices of vector potential operator ). The first is a variant of one discussed previously on this blog, in which a “neck pinch” singularity for a vortex tube is created by using a […]