Here is a curious question posed to me by Apoorva Khare that I do not know the answer to. Let be the free group on two generators
. Does there exist a metric
on this group which is
- bi-invariant, thus
for all
; and
- linear growth in the sense that
for all
and all natural numbers
?
By defining the “norm” of an element to be
, an equivalent formulation of the problem asks if there exists a non-negative norm function
that obeys the conjugation invariance
for all , the triangle inequality
for all , and the linear growth
for all and
, and such that
for all non-identity
. Indeed, if such a norm exists then one can just take
to give the desired metric.
One can normalise the norm of the generators to be at most , thus
This can then be used to upper bound the norm of other words in . For instance, from (1), (3) one has
A bit less trivially, from (3), (2), (1) one can bound commutators as
In a similar spirit one has
What is not clear to me is if one can keep arguing like this to continually improve the upper bounds on the norm of a given non-trivial group element
to the point where this norm must in fact vanish, which would demonstrate that no metric with the above properties on
would exist (and in fact would impose strong constraints on similar metrics existing on other groups as well). It is also tempting to use some ideas from geometric group theory (e.g. asymptotic cones) to try to understand these metrics further, though I wasn’t able to get very far with this approach. Anyway, this feels like a problem that might be somewhat receptive to a more crowdsourced attack, so I am posing it here in case any readers wish to try to make progress on it.

104 comments
Comments feed for this article
16 December, 2017 at 11:42 pm
Tobias Fritz
As a rather trivial observation, it may be worth noting that conjugation invariance is automatic,
16 December, 2017 at 11:52 pm
Alexander Shamov
> What is not clear to me is if one can keep arguing like this to continually improve the upper bounds on the norm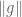 of a given non-trivial group element
of a given non-trivial group element  to the point where this norm must in fact vanish
to the point where this norm must in fact vanish
If has a nontrivial image in the abelianization then its norm definitely doesn’t have to be zero – for example, one could get a seminorm by pulling back the log of the spectral radius in a faithful representation of the abelianization of
has a nontrivial image in the abelianization then its norm definitely doesn’t have to be zero – for example, one could get a seminorm by pulling back the log of the spectral radius in a faithful representation of the abelianization of 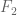 .
.
17 December, 2017 at 12:34 am
Lior Silberman
Take the direct sum of the representation and the inverse to ensure the spectral radius satisfies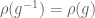 . More generally, one may take any norm on
. More generally, one may take any norm on 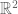 , restrict it to
, restrict it to 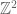 , and pull it back to
, and pull it back to 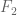 .
.
It may now be worth considering the norms on the Heisenberg group.
17 December, 2017 at 1:43 am
Will Sawin
There is no such norm on the Heisenberg group, because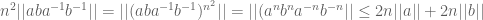 .
.
17 December, 2017 at 8:33 am
Lior Silberman
Great! This shows that every norm on a nilpotent group pulls back from the abelianization. Solvable groups are next, and I think there the situation is the same.
Can we find an example of a norm that doesn’t come from the abelianization?
17 December, 2017 at 2:07 am
Tobias Fritz
In other words, every pseudonorm on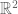 yields a linear-growth pseudometric on
yields a linear-growth pseudometric on 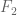 by pulling back along the abelianization map
by pulling back along the abelianization map 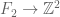 .
.
Suppose that we can show that any linear-growth pseudometric on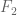 satisfies
satisfies  . Then in fact every linear-growth pseudometric comes from
. Then in fact every linear-growth pseudometric comes from 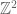 as above. To see this, let’s show first that every commutator
as above. To see this, let’s show first that every commutator  must have zero (psuedo-)norm; this is again by pulling back the norm along the homomorphism
must have zero (psuedo-)norm; this is again by pulling back the norm along the homomorphism 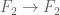 that takes
that takes 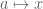 and
and  , and using the assumption. Therefore by the triangle inequality, every element of the commutator subgroup has vanishing norm, and hence the norm of an element only depends on its image in the abelianization
, and using the assumption. Therefore by the triangle inequality, every element of the commutator subgroup has vanishing norm, and hence the norm of an element only depends on its image in the abelianization 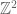 . Now it’s straightforward to see that this induces a linear-growth pseudonorm on $\mathbb{Z}^2$ which uniquely extends to a pseudonorm on $\mathbb{R}^2$ in the usual sense.
. Now it’s straightforward to see that this induces a linear-growth pseudonorm on $\mathbb{Z}^2$ which uniquely extends to a pseudonorm on $\mathbb{R}^2$ in the usual sense.
17 December, 2017 at 2:54 am
Anonymous
A natural closely related question is about uniqueness (or the number of) such metrics.
17 December, 2017 at 8:45 am
duetosymmetry
Consider making the Cayley graph of F2 in the typical way, and putting this into R^2 so that element a marches one step in the +x direction, b marches one step in the +y direction, and the opposite directions for their inverses. Then take the L1 norm on this space.
Does this satisfy the desired properties?
17 December, 2017 at 9:45 am
Terence Tao
You’ve described the pullback of a metric on , which is also being discussed in other comments. Unfortunately this metric has a kernel so is only a seminorm on
, which is also being discussed in other comments. Unfortunately this metric has a kernel so is only a seminorm on 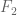 , for instance the commutator
, for instance the commutator 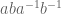 will have norm zero.
will have norm zero.
A norm on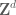 with these properties can be seen to induce a norm on the real completion
with these properties can be seen to induce a norm on the real completion 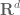 (for any vector
(for any vector 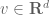 , define
, define ![\|v\| := \lim_{n \to \infty} \frac{1}{n} \| [nv] \|](https://s0.wp.com/latex.php?latex=%5C%7Cv%5C%7C+%3A%3D+%5Clim_%7Bn+%5Cto+%5Cinfty%7D+%5Cfrac%7B1%7D%7Bn%7D+%5C%7C+%5Bnv%5D+%5C%7C&bg=ffffff&fg=545454&s=0&c=20201002) where
where ![[nv]](https://s0.wp.com/latex.php?latex=%5Bnv%5D&bg=ffffff&fg=545454&s=0&c=20201002) is the nearest lattice point to
is the nearest lattice point to  (breaking ties arbitrarily)). If another group element acts by conjugation on a copy of
(breaking ties arbitrarily)). If another group element acts by conjugation on a copy of 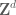 then it will induce a norm-preserving action of
then it will induce a norm-preserving action of 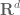 , and thus lie in the finite group
, and thus lie in the finite group  , which forces the action to be virtually trivial. I think this is enough to show that norms on finitely generated solvable groups with the stated properties have to come from the abelianisation (possibly after first passing to a finite index subgroup).
, which forces the action to be virtually trivial. I think this is enough to show that norms on finitely generated solvable groups with the stated properties have to come from the abelianisation (possibly after first passing to a finite index subgroup).
17 December, 2017 at 10:44 am
Lior Silberman
I’ve been thinking about this. Minor quibble is that the norm need not be the Euclidean one (though the isometry group is always compact). A major quibble is that a finitely generated solvable group can have infinitely generated subgroups (e.g. the lamplighter, though there I think I can show all norms are trivial on the lamps).
17 December, 2017 at 11:48 am
Terence Tao
Ah, good points! For the lamplighter, I assume you mean the lamplighter group over rather than
rather than 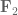 , since the torsion in the latter case would immediately make all the norms in the commutator vanish. But I don’t know how to proceed over
, since the torsion in the latter case would immediately make all the norms in the commutator vanish. But I don’t know how to proceed over  . The norm on the commutator group
. The norm on the commutator group  is shift-invariant, and the norms of vectors in this group such as
is shift-invariant, and the norms of vectors in this group such as  grow linearly in
grow linearly in  if
if  denotes the shift, but this doesn’t seem to pin down the structure further.
denotes the shift, but this doesn’t seem to pin down the structure further.
17 December, 2017 at 12:01 pm
Lior Silberman
Yes, I’m thinking of the lamplighter where $Z$ acts by translation. The norm on the lamps is a translation-invariant norm, bounded wrt the
where $Z$ acts by translation. The norm on the lamps is a translation-invariant norm, bounded wrt the 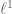 norm. The point is that if the norm on the lamps is non-zero then the conjugates of
norm. The point is that if the norm on the lamps is non-zero then the conjugates of  by a configuration of lamps of large norm have large norm, but this needs to be bounded because conjugates have the same norm.
by a configuration of lamps of large norm have large norm, but this needs to be bounded because conjugates have the same norm.
17 December, 2017 at 12:02 pm
Terence Tao
Never mind, I figured it out. If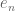 is the basis for
is the basis for  and the lamplighter is generated by
and the lamplighter is generated by 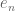 and an additional generator
and an additional generator  with
with 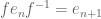 , then
, then 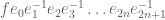 squares to something of bounded word length and thus has bounded norm (all generators
squares to something of bounded word length and thus has bounded norm (all generators 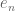 are conjugate and thus have the same norm), and hence
are conjugate and thus have the same norm), and hence  and
and  differ by bounded distance for any
differ by bounded distance for any 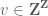 , hence
, hence  and
and 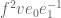 must have the same norm. But this implies that
must have the same norm. But this implies that 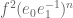 and
and 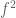 have the same norm, hence
have the same norm, hence 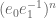 is bounded, but it must grow linearly, contradiction.
is bounded, but it must grow linearly, contradiction.
None of this sort of trickery seems to be available in the free group, though…
18 December, 2017 at 2:28 pm
Lior Silberman
Not applicable to the free group, but this lamplighter group is kind of a free solvable group on two generators, so this argumetn is enough to show that every norm on a solvable group comes from the abelianization.
17 December, 2017 at 9:52 am
Lior Silberman
Worth noting that in any group the elements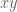 and
and 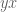 are conjugate, so the norm of non-commutators must arise from a norm on the abelianization.
are conjugate, so the norm of non-commutators must arise from a norm on the abelianization.
17 December, 2017 at 11:46 am
Will Sawin
I don’t think “non-commutators” is a rigorous concept here. The key point is that conjugation shows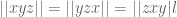 but not anything about how this compares to
but not anything about how this compares to 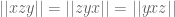 , even though all six agree on the abelianization.
, even though all six agree on the abelianization.
17 December, 2017 at 12:06 pm
Andy Putman
I haven’t had time to carefully read through all the comments, but I thought I’d throw out the following simple idea. Let be any generating set for
be any generating set for 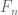 that is closed under conjugation (such an
that is closed under conjugation (such an  must be infinite) and define the
must be infinite) and define the  -norm on
-norm on 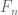 to be the word length with respect to
to be the word length with respect to  . It is clear that this satisfies conjugation-invariance and the triangle inequality, so the key is finding an
. It is clear that this satisfies conjugation-invariance and the triangle inequality, so the key is finding an  where the norm satisfies linear growth. There are a whole ton of possible choices of
where the norm satisfies linear growth. There are a whole ton of possible choices of  that might work. One attractive possibility is taking
that might work. One attractive possibility is taking  to be the set of primitive elements, that is, elements that form part of a free basis.
to be the set of primitive elements, that is, elements that form part of a free basis.
An interesting observation is that the above “primitive element norm” is actually invariant under all automorphisms of the free group (not just inner automorphisms).
17 December, 2017 at 1:09 pm
Lior Silberman
The element is primitive, so you won’t get linear growth this way.
is primitive, so you won’t get linear growth this way.
17 December, 2017 at 1:11 pm
Andy Putman
Good point Lior! Another possibility would be to take to be the set of all conjugates of the usual free basis for
to be the set of all conjugates of the usual free basis for 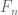 .
.
17 December, 2017 at 1:15 pm
Tobias Fritz
Terry’s original bound of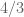 shows that if you use a word metric, then your generating set
shows that if you use a word metric, then your generating set  must be closed under commutators.
must be closed under commutators.
17 December, 2017 at 1:23 pm
Andy Putman
Is that so? His 4/3 bound concerned the norm not of a general commutator, but rather of the commutator of two elements in the standard free basis. But I agree that in my suggested the norm of [a,b] would be 2, and thus would violate Terry’s bound.
the norm of [a,b] would be 2, and thus would violate Terry’s bound.
One obvious thing to try to do would be to symmetrize a (conjugation-invariant) word norm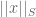 by letting
by letting 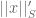 equal the limit as
equal the limit as  goes to infinity of
goes to infinity of  (this limit clearly exists). We then clearly have
(this limit clearly exists). We then clearly have 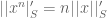 , and the triangle inequality holds. What might go wrong is that it is possible for
, and the triangle inequality holds. What might go wrong is that it is possible for 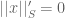 for some nontrivial
for some nontrivial  .
.
17 December, 2017 at 1:39 pm
Tobias Fritz
Well, Terry’s estimate in its general form is![||[x,y]||\leq\tfrac{2}{3}(||x|| + ||y||)](https://s0.wp.com/latex.php?latex=%7C%7C%5Bx%2Cy%5D%7C%7C%5Cleq%5Ctfrac%7B2%7D%7B3%7D%28%7C%7Cx%7C%7C+%2B+%7C%7Cy%7C%7C%29&bg=ffffff&fg=545454&s=0&c=20201002) for arbitrary
for arbitrary 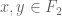 , using verbatim the same argument for the proof. Since an element is in
, using verbatim the same argument for the proof. Since an element is in  if and only if its word norm is 1, we can conclude that
if and only if its word norm is 1, we can conclude that  implies
implies ![[x,y]\in S](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%5Cin+S&bg=ffffff&fg=545454&s=0&c=20201002) .
.
I had also considered your suggestion of taking , but it wasn’t clear to me how to prove the triangle inequality. This is straightforward (and standard) in the commutative case, but in a noncommutative group I don’t know what to do with
, but it wasn’t clear to me how to prove the triangle inequality. This is straightforward (and standard) in the commutative case, but in a noncommutative group I don’t know what to do with  , and would suspect the triangle inequality to be violated in general. Any thoughts?
, and would suspect the triangle inequality to be violated in general. Any thoughts?
For example, stable commutator length seems to be a quantity of this type, defined on the commutator subgroup of a group where is taken to be the set of commutators. Does it satisfy the triangle inequality?
is taken to be the set of commutators. Does it satisfy the triangle inequality?
17 December, 2017 at 5:59 pm
Andy Putman
You’re absolutely right about the triangle inequality. I’m not sure what I was thinking.
18 December, 2017 at 4:26 am
Will Sawin
It seems likely not. It’s known that if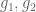 are elements of infinite order in (the commutator subgroups of) groups
are elements of infinite order in (the commutator subgroups of) groups  , then
, then 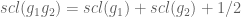 where
where  is taken in the free product
is taken in the free product  (Theorem 2.93 in scl by Danny Calegari, originally due to Christophe Bavard, though apparently not with a correct proof). So in particular the triangle inequality fails in the free group on four generators
(Theorem 2.93 in scl by Danny Calegari, originally due to Christophe Bavard, though apparently not with a correct proof). So in particular the triangle inequality fails in the free group on four generators  for the product of a commutator in the free group on
for the product of a commutator in the free group on 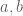 and one in the free group on
and one in the free group on 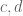 .
.
17 December, 2017 at 7:50 pm
Anonymous
Perhaps the existence of an invariant norm satisfying (1)-(3) may be proved by a method similar to the proof of the existence of Haar measure?
17 December, 2017 at 9:15 pm
Siddhartha Gadgil
Some simple remarks:![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=545454&s=0&c=20201002) , there is one for all elements.
, there is one for all elements.
* The maximum, or supremum of a set of linear semi-norms with norms of generators bounded above by 1 is a linear semi-norm.
* Hence we have a canonical semi-norm, the largest linear semi-norm for which the generators have norm at most one.
* The question is thus reduced to whether this is a norm, or equivalently whether for a specific element g in the free group, there exists a linear semi-norm which is positive on g.
* I would guess that if there is such a semi-norm for the commutator
17 December, 2017 at 11:01 pm
Siddhartha Gadgil
A very speculative construction of such a norm:
We take a linear combination of two terms associated to a word , with the second having a very small coefficient.
, with the second having a very small coefficient. such that a letter is matched to an inverse letter (i.e., pairs of indices
such that a letter is matched to an inverse letter (i.e., pairs of indices 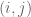 such that
such that  and
and  are inverses). For such matchings, we consider the number of crossings (pair of pairs
are inverses). For such matchings, we consider the number of crossings (pair of pairs 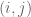 and
and  with
with 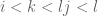 after flips if necessary). We associate to the word the minimum number of crossings over all matchings.
after flips if necessary). We associate to the word the minimum number of crossings over all matchings.
(1) The norm in the abelianisation.
(2′) Consider maximal matchings of the letters of
(2) We need to make (2') linear by taking powers and limits as usual.
The minimal number of crossings does satisfy the triangle inequality. What we need is the norm after the linearization correction also does so.
18 December, 2017 at 12:22 am
cjerdonek
I could be off here, but why doesn’t it work to take a compact hyperbolic surface with geodesic boundary whose fundamental group is the free group on two generators (e.g. a “pair of pants”), and then define the norm to be the length of the free geodesic representing the element?
18 December, 2017 at 12:50 am
Siddhartha Gadgil
This fails the triangle inequality (I assume you mean the geodesic representing a conjugacy class)
18 December, 2017 at 12:49 am
Siddhartha Gadgil
An addendum: one can clearly do a Kobayashi-style construction to get the triangle inequality, so the question is whether after all this we get positivity.
18 December, 2017 at 2:23 am
Siddhartha Gadgil
Just a clean up of the above, the main idea is to consider the following function of a word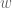 in the free group:
in the free group:
(1) Consider partial matchings of the letters without crossing and so that letters can only be matched with their inverse.
(2) For such a matching, we count the number of letters that are unmatched.
(3) Minimize this over all such partial matchings
This may even be a linear norm – if not I conjecture that after the usual constructions to make it linear and a norm, we still get positivity (related stuff is in arXiv:0809.3110)
Incidentally, for the commutator![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=545454&s=0&c=20201002) , the value of the function is exactly 2, the Tao bound.
, the value of the function is exactly 2, the Tao bound.
18 December, 2017 at 4:59 am
Tobias Fritz
What are “the usual constructions” to make it linear and a norm?
Over in the other thread, we ran into the problem that it’s not clear whether linearizing via retains the triangle inequality. And as Will pointed out, stable commutator length is essentially a counterexample (taking it to be infinite on elements that are not commutators).
retains the triangle inequality. And as Will pointed out, stable commutator length is essentially a counterexample (taking it to be infinite on elements that are not commutators).
On the other hand, when starting with a linear quantity and enforcing the triangle inequality by taking shortest paths, it’s also not obvious why linearity would be preserved, or is it?
So in general, it may be that one has to iterate both constructions, resulting in an infinite regress.
18 December, 2017 at 5:50 am
Siddhartha Gadgil
That’s true, one may in general have to iterate infinitely often, so the key is to understand to what extent linearity fails for the “unmatched letters” function, and control the process. Triangle inequality clears holds (but will be in general broken by linearization).
18 December, 2017 at 9:16 am
Terence Tao
A small observation: the linear growth and conjugation invariance axioms for the norm can be replaced without loss of generality to just the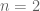 case
case  of the linear growth axiom. This implies
of the linear growth axiom. This implies  for
for  a power of two, while the triangle inequality gives
a power of two, while the triangle inequality gives  for all positive
for all positive  ; since any natural number is eventually upper bounded by a power of two, the triangle inequality again then gives
; since any natural number is eventually upper bounded by a power of two, the triangle inequality again then gives 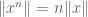 for all positive
for all positive  . Finally, replacing
. Finally, replacing 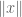 with
with 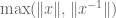 gives the negative
gives the negative  cases of the linear growth axiom, and Tobias’s observation then recovers the conjugation invariance axiom.
cases of the linear growth axiom, and Tobias’s observation then recovers the conjugation invariance axiom.
Equivalently, the problem may be reduced to the following. Is there a function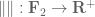 such that
such that 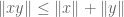 for all
for all 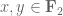 with equality whenever
with equality whenever 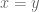 , such that
, such that 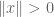 for all non-identity
for all non-identity  ?
?
18 December, 2017 at 11:56 am
Anonymous
It seems that one can take the norm of to be the minimal length over all the words conjugate to it. (the norm of the identity is defined to be 0).
to be the minimal length over all the words conjugate to it. (the norm of the identity is defined to be 0).
18 December, 2017 at 11:00 am
Anonymous
Let be the Levenshtein distance defined on the set of all strings on 5 alphabets
be the Levenshtein distance defined on the set of all strings on 5 alphabets 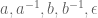 . Note that
. Note that  represents the empty string. Let further identify
represents the empty string. Let further identify 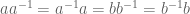 with
with  . Under this identification, each element of
. Under this identification, each element of 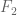 can be uniquely identified with a string with minimum length. For example, the string
can be uniquely identified with a string with minimum length. For example, the string 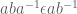 is
is  . Under this identification, I think the Levenshtein distance is well defined on
. Under this identification, I think the Levenshtein distance is well defined on 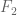 and has all the desired properties.
and has all the desired properties.
18 December, 2017 at 12:35 pm
Lior Silberman
Interesting idea, but it can’t work as stated: edit distance is always an integer while as noted above commutators have norm at most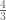 .
.
18 December, 2017 at 2:03 pm
Terence Tao
Ultimately the problem is that there are words (such as
(such as 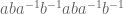 ) for which one can efficiently edit
) for which one can efficiently edit  to the identity in a manner that is cheaper than editing the two copies of
to the identity in a manner that is cheaper than editing the two copies of  to the identity separately.
to the identity separately.
Here is another idea I had for constructing a norm, coming from functional analysis. If one assigns unitary operators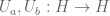 on a Hilbert space, then this generates a unitary representation
on a Hilbert space, then this generates a unitary representation 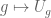 on the free group. It is then tempting to define
on the free group. It is then tempting to define  to be some conjugation invariant operator norm of the difference
to be some conjugation invariant operator norm of the difference 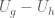 , such as a Schatten p-norm
, such as a Schatten p-norm 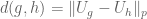 . The problem is that this doesn’t obey the doubling property. However, it comes close to obeying doubling near the origin of the spectrum, so one could imagine trying some sort of asymptotic Schatten p-norm such as
. The problem is that this doesn’t obey the doubling property. However, it comes close to obeying doubling near the origin of the spectrum, so one could imagine trying some sort of asymptotic Schatten p-norm such as 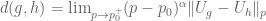 for a suitable exponent
for a suitable exponent  , where
, where 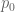 is some sort of critical exponent whose Schatten class the differences
is some sort of critical exponent whose Schatten class the differences 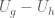 just fail to live in, as this sort of limit will be insensitive to the portion of the spectrum away from the origin, and one recovers doubling after taking a limit. Unfortunately the problem is that the commutator
just fail to live in, as this sort of limit will be insensitive to the portion of the spectrum away from the origin, and one recovers doubling after taking a limit. Unfortunately the problem is that the commutator ![[U_g,U_h] - 1](https://s0.wp.com/latex.php?latex=%5BU_g%2CU_h%5D+-+1&bg=ffffff&fg=545454&s=0&c=20201002) tends to have much better Schatten properties than
tends to have much better Schatten properties than 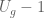 or
or 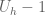 (the former is essentially the Lie bracket of the latter, up to conjugation) and so all the implementations of this idea I tried produced a seminorm that vanished on commutators, much as with previous constructions. But maybe some variant of this construction will work (I’m pretty sure one needs an infinite dimensional representation though, for finite dimensional reps the doubling condition is way too limiting.)
(the former is essentially the Lie bracket of the latter, up to conjugation) and so all the implementations of this idea I tried produced a seminorm that vanished on commutators, much as with previous constructions. But maybe some variant of this construction will work (I’m pretty sure one needs an infinite dimensional representation though, for finite dimensional reps the doubling condition is way too limiting.)
18 December, 2017 at 8:52 pm
dcohen
What’s wrong with taking two generic positive symmetric matrices instead, and considering the logarithm of the condition number?
18 December, 2017 at 9:07 pm
dcohen
or actually two generic matrices without restrictions
19 December, 2017 at 7:53 pm
alexmaplegm
Why do you expect this to to obey the triangle inequality?
18 December, 2017 at 9:52 pm
dcohen
sorry, symmetry is required obviously for the condition number to work, obviously
18 December, 2017 at 3:27 pm
Anonymous
Is it clear that such metric exists on words with length bounded by let’s say 100?
19 December, 2017 at 7:49 am
Anonymous
This problem of assigning norm values to words of bounded length (for any given fixed bound) can be formulated as a linear programming problem – for which the existence of admissible norm values can be decided.
19 December, 2017 at 9:56 am
Anonymous
Exactly. I just wondered if somebody ran it for small values.
19 December, 2017 at 10:32 am
Lior Silberman
There are about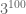 elements in the ball of radius
elements in the ball of radius 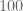 , so we won’t be checking that by computer. On the other hand, even the
, so we won’t be checking that by computer. On the other hand, even the 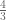 bound on commutators was obtained above by considering
bound on commutators was obtained above by considering ![[a,b]^3](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%5E3&bg=ffffff&fg=545454&s=0&c=20201002) which has word length
which has word length 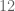 . In short, I find it hard to believe that you’ll get something non-trivial at radii which are computationally accessible. That said, I’d be very happy to be proven wrong.
. In short, I find it hard to believe that you’ll get something non-trivial at radii which are computationally accessible. That said, I’d be very happy to be proven wrong.
19 December, 2017 at 1:24 pm
Pace Nielsen
By putting together the two bounds Terry gave, we get that commutators of the generators are bounded in norm by 5/4, which improves over 4/3.
and that last quantity has norm at most 2 (by Terry’s second argument). This idea might be useful to push things further.
has norm at most 2 (by Terry’s second argument). This idea might be useful to push things further.
19 December, 2017 at 1:53 pm
Anonymous
Perhaps there is a generalization of such identities for higher powers of the commutators (or some recursive relations among consecutive powers) to push the bound arbitrarily close to 1 ?
19 December, 2017 at 1:59 pm
Tobias Fritz
This is exciting! There are indeed commutator formulas that could be related, but previously I hadn’t seen concretely how we could apply them to derive better bounds. Perhaps Pace’s new observation can provide some guidance here.
19 December, 2017 at 2:33 pm
Terence Tao
Ad hoc iteration of this seems to give further improvements. Firstly, the argument bounding in the blog post more generally gives
in the blog post more generally gives
for any , and similarly for other words that are similar to
, and similarly for other words that are similar to 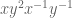 , such as
, such as 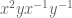 . Your argument then gives
. Your argument then gives
(side note: curious that the LHS is symmetric in but the RHS is not) and in particular
but the RHS is not) and in particular
improving over the more obvious upper bound of 2 coming from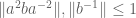 .
.
On the other hand, your argument also gives
which is a small improvement over the previous bound of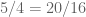 . It looks like some further improvement is possible by additional iteration, though I’m not seeing a fully systematic way to keep doing this. As mentioned previously, a completely brute force search is likely to be computationally infeasible, but maybe there is still some scope for computer assisted location of bounds here?
. It looks like some further improvement is possible by additional iteration, though I’m not seeing a fully systematic way to keep doing this. As mentioned previously, a completely brute force search is likely to be computationally infeasible, but maybe there is still some scope for computer assisted location of bounds here?
19 December, 2017 at 3:51 pm
Lior Silberman
If I haven’t made an error, I think we have the identity![[x,y]^k = (xyx)\left(x^{-2}y^{-1}xy[x^{-1},y^{-1}]^{k-3}\right)(xyx)^{-1} (x^2yx^{-1}y^{-1})](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%5Ek+%3D+%28xyx%29%5Cleft%28x%5E%7B-2%7Dy%5E%7B-1%7Dxy%5Bx%5E%7B-1%7D%2Cy%5E%7B-1%7D%5D%5E%7Bk-3%7D%5Cright%29%28xyx%29%5E%7B-1%7D+%28x%5E2yx%5E%7B-1%7Dy%5E%7B-1%7D%29&bg=ffffff&fg=545454&s=0&c=20201002) and hence
and hence ![\Vert [x,y]\Vert \leq \frac13\left(\Vert x^{-2} y^{-1} xy\Vert + \Vert x^2 y x^{-1}y^{-1}\Vert\right)](https://s0.wp.com/latex.php?latex=%5CVert+%5Bx%2Cy%5D%5CVert+%5Cleq+%5Cfrac13%5Cleft%28%5CVert+x%5E%7B-2%7D+y%5E%7B-1%7D+xy%5CVert+%2B+%5CVert+x%5E2+y+x%5E%7B-1%7Dy%5E%7B-1%7D%5CVert%5Cright%29&bg=ffffff&fg=545454&s=0&c=20201002) that is
that is
19 December, 2017 at 4:10 pm
Apoorva Khare
Does the 7/4 show up for the word you are using too, Lior, or is it for a commutator like Terry wrote? (I had obtained the same identity, but wasn’t sure how to beat 2 for that word.)
19 December, 2017 at 4:29 pm
Apoorva Khare
@Lior: could you please elaborate on the use of 7/4 here? (I had worked out the same identity, but didn’t see how to plug in 7/4 in it instead of 2.)
19 December, 2017 at 8:14 pm
Lior Silberman
You’re right — it should have been 2.
19 December, 2017 at 3:16 pm
Apoorva Khare
This is very exciting! I’ll just add a few remarks here.
(1) The observation that Terry made about linear growth being equivalent to “doubling” (norm(x^2) = 2*norm(x)) can also be found in the preprint http://arxiv.org/abs/1610.03037
(2) The preprint explores how *abelian* groups with linear growth embed into “minimal” vector spaces, and those into “minimal” Banach spaces – whence the linear growth is just the property of the norm. Two corresponding questions in the non-abelian setting would be:
(i) Do such non-abelian groups with linear growth exist in the first place? In particular, if they do, restrict to the subgroup generated by two non-commuting elements a,b.
(ii) Would such a group embed into a “geodesically” closed group, say a connected Lie group?
The latter question can be answered negatively: by Lemma 7.5 in Milnor’s 1976 Advances paper
http://www.sciencedirect.com/science/article/pii/S0001870876800023
every such group would be (compact) x (abelian); but the (compact) has torsion so much be trivial, and then (abelian) cannot work. So there are no such Lie groups, whence no embedding. This leaves the former question.
(3) A small typo, in Terry’s latest computation involving 19/16: the last b^{-1} should be b. [Corrected – T.]
19 December, 2017 at 4:19 pm
António Machiavelo
A very simple remark that may be worth noticing is that, for all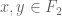 , one has
, one has 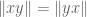 . This follows from the fact that, for all
. This follows from the fact that, for all  ,
,  .
.
19 December, 2017 at 4:38 pm
Apoorva Khare
Taking a step back, notice that *all* bounds obtained so far on the norm of [a,b], are above 1. And we want to get this estimate down to zero!
What kind of technique or result would (at least) push the bound below 1? Do we think that current techniques will do so?
19 December, 2017 at 4:56 pm
Apoorva Khare
(PS. Perhaps stating the obvious: can this in fact be done at all?)
19 December, 2017 at 5:25 pm
Anonymous
Perhaps a related question is about possible derivation (by similar methods) of some nontrivial (i.e. positive) lower(!) bounds on commutators norms.
19 December, 2017 at 5:22 pm
Pace Nielsen
I have to get home soon, so I ran out of time to work out exactly what happens, but I thought I’d share another observation now so people can play with it:
Thus, the bound on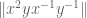 improves as the bound on
improves as the bound on  improves. This quantity improves as the bound on
improves. This quantity improves as the bound on 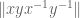 improves, and this in turn improves as bounds on the first quantity improve. [There is also the possibility that simultaneously playing with
improves, and this in turn improves as bounds on the first quantity improve. [There is also the possibility that simultaneously playing with  might help too.] I got at down to 37/32 after one iteration of this idea.
might help too.] I got at down to 37/32 after one iteration of this idea.
19 December, 2017 at 7:10 pm
Terence Tao
One could start automating this to some extent. We are finding a number of inequalities of the form
or
for various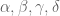 . For instance (1) holds for
. For instance (1) holds for  , while (2) holds for
, while (2) holds for  . We now also have a number of rules that allow one to convert existing bounds to other ones. For instance your argument shows that if (1) holds for
. We now also have a number of rules that allow one to convert existing bounds to other ones. For instance your argument shows that if (1) holds for 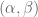 then (2) holds for
then (2) holds for  . Swapping
. Swapping  we also know that if (1) holds for
we also know that if (1) holds for 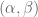 then (1) also holds for
then (1) also holds for  . Lior’s identity shows that if (2) holds for
. Lior’s identity shows that if (2) holds for  then (1) holds for
then (1) holds for  . My previous argument shows (I think) that if (1) holds for
. My previous argument shows (I think) that if (1) holds for 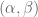 and (2) holds for
and (2) holds for  , then (1) holds for
, then (1) holds for  . Perhaps one could start collecting more implications like this and then use a computer to iterate and optimise?
. Perhaps one could start collecting more implications like this and then use a computer to iterate and optimise?
19 December, 2017 at 8:29 pm
Anonymous
One may try also to derive similar lower bounds on the norms (which may be used to prove that such a metric can’t exist if after optimization they become larger than the corresponding optimized upper bounds)
19 December, 2017 at 8:47 pm
Lior Silberman
Assuming we expect![\Vert[x,y]\Vert=0](https://s0.wp.com/latex.php?latex=%5CVert%5Bx%2Cy%5D%5CVert%3D0&bg=ffffff&fg=545454&s=0&c=20201002) I’d replace
I’d replace 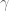 with
with 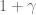 .
.
Also, we know that if (1) holds for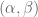 it also holds for
it also holds for  . This is a contracting map with fixed point
. This is a contracting map with fixed point 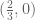 .
.
Did I make a mistake?
19 December, 2017 at 8:56 pm
Lior Silberman
Of course I did. The fixed point is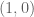 .
.
19 December, 2017 at 8:57 pm
Apoorva Khare
That looks right to me! I was working very crudely it seems.
Now just start with e.g. (0,2), and one gets to (2/3,0). We are below 1!
19 December, 2017 at 9:01 pm
Apoorva Khare
Aha, even I got carried away. But then my original point remains: can we check starting with (0,2) that we might come below 1? Or use Terry’s bound at some point.
The fixed point is (1,0), but as long as we can approach it from below…
(Sorry, I’m attending a conference in honor of Thangavelu here, so cannot work it out right now…)
19 December, 2017 at 9:16 pm
Lior Silberman
But the following is correct: iterating gives the fixed point
gives the fixed point 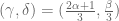 .
.
Using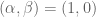 we get
we get  which is exciting to me because that’s the bound consistent with
which is exciting to me because that’s the bound consistent with ![\Vert[x,y]\Vert = 0](https://s0.wp.com/latex.php?latex=%5CVert%5Bx%2Cy%5D%5CVert+%3D+0&bg=ffffff&fg=545454&s=0&c=20201002) .
.
19 December, 2017 at 9:57 pm
Lior Silberman
Something is wrong somewhere: if the fixed point really were correct then using the admissible value
really were correct then using the admissible value 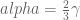 gives the transformation
gives the transformation  with fixed point
with fixed point 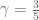 . It follows that we can take
. It follows that we can take 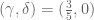 and
and  .
.
Unfortunately, it should be impossible to take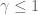 because there exist norms vanishing on the commutators and for those
because there exist norms vanishing on the commutators and for those
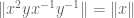 independently of
independently of  .
.
19 December, 2017 at 10:16 pm
Terence Tao
The problem is that the pair is a pair for the
is a pair for the 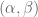 inequality, not the
inequality, not the  inequality, so the iteration doesn’t work.
inequality, so the iteration doesn’t work.
I’ve written up the arguments that I was able to check were correct, and put then on a fresh blog post. Given the large number of comments on this thread, it is probably best for everyone to move over to the new post (as per the polymath projects, which I guess this question has become a de facto version of).
19 December, 2017 at 9:05 pm
Anonymous
The pair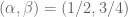 is equivalent to
is equivalent to 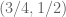 which (by taking their mean) implies the pair
which (by taking their mean) implies the pair  which is better than
which is better than 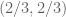 .
.
19 December, 2017 at 8:09 pm
Apoorva Khare
Very nice – in that case I think we can cross below the magic bound of 1 at least, in Equation (1)! Here’s how: let A = \alpha + \beta, C = \gamma + \delta.
Start with (1) for \alpha = 1/2, \beta = 3/4, so A = 5/4.
By iteratively applying Lior and Pace alternately, we converge to A = 1, C = 3/2.
But now once we get close enough to these values, apply Terry’s previous argument. This will get us close to A = 7/8, which means we are below 1.
(If I did the math correctly.)
19 December, 2017 at 8:15 pm
Apoorva Khare
Oops, I was using the wrong bound. My crude estimates suggest we will get to something not close to 7/8 (as I’d just written), but to something bounded *above* by 9/8. Exactly what it is (i.e. \leq 1 or not) should be computable by examining not just A,C, but what \alpha and \beta become in the limit.
19 December, 2017 at 9:22 pm
Anonymous
Here’s a proof that we can assume the norm is invariant to natural symmetries (so we get for instance that ).
).
Let be the “inversing
be the “inversing  ” map (e.g.
” map (e.g.  ) and
) and 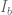 be analogous. Let
be analogous. Let  be the “switch” map, switching
be the “switch” map, switching  and
and 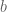 (e.g.
(e.g.  ). Then
). Then 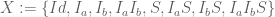 is invariant to left multiplication by any of its elements.
is invariant to left multiplication by any of its elements.
So, if we have any norm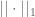 , we can form a norm
, we can form a norm 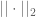 by
by 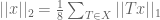 . Since for any
. Since for any  and any
and any  ,
, 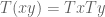 , it is easy to see that
, it is easy to see that 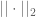 also satisfies the requirements (cf Terry’s simplification in one of the comments) and is invariant to any
also satisfies the requirements (cf Terry’s simplification in one of the comments) and is invariant to any  .
.
19 December, 2017 at 9:31 pm
Siddhartha Gadgil
Looks like some computer searching does give a bound on the commutator that is below 1. If correct I will get “proofs” output by the same code soon.
19 December, 2017 at 9:42 pm
Pace Nielsen
We can get below 1 (as others seem to have recognized). Here is one way:
We previously derived . Plugging this into the general argument Terry gave, which was used to get the bound 19/16, yields
. Plugging this into the general argument Terry gave, which was used to get the bound 19/16, yields  .
.
Now, if , then
, then 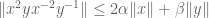 . So, plugging this into the formula above we reach
. So, plugging this into the formula above we reach 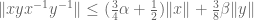 . By symmetry, we have the corresponding inequality with those same coefficients switched. Thus if we set
. By symmetry, we have the corresponding inequality with those same coefficients switched. Thus if we set 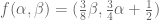 , the output is a valid set of new
, the output is a valid set of new 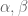 coefficients. Starting with
coefficients. Starting with 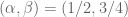 the fifth iteration has a sum below 1. It appears to converge to about
the fifth iteration has a sum below 1. It appears to converge to about  .
.
19 December, 2017 at 10:04 pm
Lior Silberman
The map is evidently contracting, so the iterates will converge to the fixed point which is
is evidently contracting, so the iterates will converge to the fixed point which is 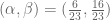 .
.
19 December, 2017 at 10:06 pm
Lior Silberman
Adding that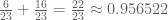 .
.
19 December, 2017 at 10:16 pm
Bi-invariant metrics of linear growth on the free group, II | What's new
[…] Terence Tao on Bi-invariant metrics of linear… […]
19 December, 2017 at 11:03 pm
dcohen
Let’s first build such a “norm” on the kernel of the natural map from
of the natural map from 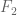 to
to 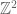 . An element in
. An element in  is an equivalence class of closed loops based at
is an equivalence class of closed loops based at  on
on 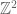 , two loops being equivalent if they are the same “modulo backtracking”. Now consider the area enclosed by the loop, more precisely the integral over
, two loops being equivalent if they are the same “modulo backtracking”. Now consider the area enclosed by the loop, more precisely the integral over 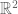 of the absolute value of the winding number. This only depends on the equivalence class and satisfies the conditions. To extend this norm to
of the absolute value of the winding number. This only depends on the equivalence class and satisfies the conditions. To extend this norm to 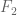 , one can set the norm of the elements outside
, one can set the norm of the elements outside  to be the norm of their image in
to be the norm of their image in 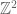 .
.
19 December, 2017 at 11:51 pm
Terence Tao
Unfortunately once one enlarges , one ceases to be a norm. For instance, with your construction, the word
, one ceases to be a norm. For instance, with your construction, the word  has norm
has norm 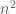 , but by the triangle inequality it can only have norm
, but by the triangle inequality it can only have norm  once one is allowed to use the generators outside of
once one is allowed to use the generators outside of  , leading to a contradiction when
, leading to a contradiction when  is large. (There is also a secondary issue, namely that there are some non-trivial elements of
is large. (There is also a secondary issue, namely that there are some non-trivial elements of  that continue to have zero norm because the winding numbers all cancel each other out.) The obstructions here are related to those showing that there are no seminorms on nilpotent groups other than those coming from the abelianisation.
that continue to have zero norm because the winding numbers all cancel each other out.) The obstructions here are related to those showing that there are no seminorms on nilpotent groups other than those coming from the abelianisation.
However, this does raise an interesting question: what additional conditions of a norm on are sufficient to permit an extension to all of
are sufficient to permit an extension to all of 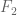 ? The question may be easier if one looks at the kernel of a map to
? The question may be easier if one looks at the kernel of a map to  rather than to
rather than to  (e.g. the homomorphism that sends
(e.g. the homomorphism that sends  to
to  and annihilates
and annihilates 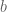 ).
).
20 December, 2017 at 12:10 am
Tobias Fritz
And again, this is an example of a seminorm that arises by pullback from the abelianization: if and
and  are closed loops, then the oriented area enclosed by
are closed loops, then the oriented area enclosed by  is zero.
is zero.
20 December, 2017 at 8:00 pm
Siddhartha Gadgil
One can get a bound on the commutator of 0.816 with a brutal proof (not optimized by any means). The proof (computer generated but formatted to be readable) is at
https://github.com/siddhartha-gadgil/Superficial/wiki/A-commutator-bound
Comments welcome. Someone cleverer may extract useful inequalities from this (or find an error).
20 December, 2017 at 9:40 pm
Pace Nielsen
This was beautiful! My intuition was, before scouring your file, that we now have strong evidence that the norm will be forced to equal zero on commutators. Thus, elements like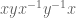 should have norm the same as
should have norm the same as  . Our job is then to bound the norm of words like
. Our job is then to bound the norm of words like 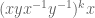 (for larger and larger values of
(for larger and larger values of  ) nearer and nearer the norm of
) nearer and nearer the norm of  .
.
I was surprised, when reading your file, that this seems to be the path that the computer has taken, with a few additional ideas thrown in. The first 43 lines establish
and lines 44 to 73 establish
(which, incidentally, gives a new value). Lines 74 to 119, using these previous bounds, establishe a similar type of bound on
value). Lines 74 to 119, using these previous bounds, establishe a similar type of bound on 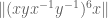 . And the last few lines use this information to bound the norm of a commutator.
. And the last few lines use this information to bound the norm of a commutator.
This was very well done!
We can improve the first computation to the bound
as follows. Let be an extremely large power. Then (following what the computer did), when we expand
be an extremely large power. Then (following what the computer did), when we expand 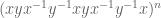 it has two
it has two  ‘s on the edges, which we peel off, and the rest looks like
‘s on the edges, which we peel off, and the rest looks like
where the dots in the middle means that this pattern repeats inwardly. [Note: When writing powers in variables I’m just using the standard conjugation notation.] This pattern continues until we reach the very middle, where there are a bounded number of terms that don’t fit this pattern. Thus,
I’ll take a look at the computer’s bound on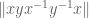 to see if we can get a similar improvement.
to see if we can get a similar improvement.
P.S. I’ll probably post anything I find to the newer thread Terry created.
21 December, 2017 at 8:50 am
Terence Tao
Pace, I’m not able to verify the identity for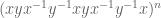 you’ve claimed above. Could you elaborate on what “repeating inwardly” means, perhaps by supplying the next few terms in the
you’ve claimed above. Could you elaborate on what “repeating inwardly” means, perhaps by supplying the next few terms in the 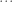 ?
?
EDIT: Never mind, I figured it out (thanks also to Pace for simultaneously communicating this), as you keep going inwards you keep on conjugating further, so your expansion is of the form
where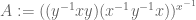 and
and 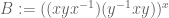 .
.
20 December, 2017 at 9:49 pm
Lior Silberman
Wow. How did you find this? There’s no way you did a computation on the entire ball of radius 500.
20 December, 2017 at 10:18 pm
Pace Nielsen
Now to explicate lines 44-73. The pattern found by the computer gives the bounds
This is derived in a manner similar to what I did above. Taking a very large power of , and dropping the last
, and dropping the last  , it has the pattern
, it has the pattern
where again the dots means the pattern repeats inward (with some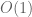 terms in the middle). Now
terms in the middle). Now  has norm bounded by
has norm bounded by  so the result follows.
so the result follows.
21 December, 2017 at 2:35 am
Tobias Fritz
What amazing developments!
Especially this inward-repetition method seems quite powerful. So why not apply it to the commutator itself? Like this, I think I can show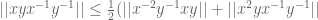 . The reason is that a high power of the commutator gives the inward repeating pattern
. The reason is that a high power of the commutator gives the inward repeating pattern
ignoring edge and centre terms. This pattern is the same as
Since per pattern, this corresponds to four copies of the commutator, we obtain the claimed bound.
I’ve lost track of the current best bounds on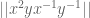 , so I’m not sure about how this compares with the other results that we have so far. But I’ll keep trying to get down to
, so I’m not sure about how this compares with the other results that we have so far. But I’ll keep trying to get down to  .
.
21 December, 2017 at 2:53 am
Tobias Fritz
Whoops, I meant half of that,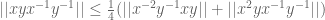 .
.
In terms of yesterday’s Proposition 1, this now genuinely improves upon (iii): If (2) holds for , then (1) holds for
, then (1) holds for  .
.
Since we (and especially me) have already made so many small mistakes that resulted in incorrect claims, I’d appreciate it if somebody else could double-check this.
21 December, 2017 at 5:22 am
Apoorva Khare
I did double-check this part. It worked out the same for me.
21 December, 2017 at 3:15 am
António Machiavelo
As I have noted in a small note on the continuation of this post, is bounded from below by the max of the norms of
is bounded from below by the max of the norms of  .
.
21 December, 2017 at 9:16 am
Pace Nielsen
I think that you showed it is it is bounded below by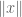 . (Your argument, and the quantity to be bounded, is not symmetric in arbitrary
. (Your argument, and the quantity to be bounded, is not symmetric in arbitrary  .)
.)
21 December, 2017 at 11:18 am
António Machiavelo
Yes, you are right, of course. I should have been more careful with this last post.
21 December, 2017 at 12:05 am
Siddhartha Gadgil
I should clarify how the computer found these – I tried various constructions of norms, which were all obstructed by lack of linearity on elements , so I explicitly looked at such elements. In particular the k=6 I had earlier found was useful.
, so I explicitly looked at such elements. In particular the k=6 I had earlier found was useful.
The bound has improved since then (to about .75), but with longer proofs. The code is open sourced in the same repository where this proof is, i.e. at https://github.com/siddhartha-gadgil/Superficial, specifically the package https://github.com/siddhartha-gadgil/Superficial/tree/master/src/main/scala/freegroups but has to be run in a console.
21 December, 2017 at 12:15 am
Pace Nielsen
You can avoid , and get the better bound
, and get the better bound 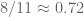 , using the recent idea of Tobias. Take the 11th power of
, using the recent idea of Tobias. Take the 11th power of 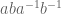 and note this is a product of four equal length monomials, each conjugate to something that looks like
and note this is a product of four equal length monomials, each conjugate to something that looks like 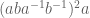 . By the work above, each is bounded in norm by 2.
. By the work above, each is bounded in norm by 2.
21 December, 2017 at 12:29 am
Lior Silberman
Ah —![[x,y]^kx](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%5Ekx&bg=ffffff&fg=545454&s=0&c=20201002) is the point. I was looking at
is the point. I was looking at ![x^k[x,y]](https://s0.wp.com/latex.php?latex=x%5Ek%5Bx%2Cy%5D&bg=ffffff&fg=545454&s=0&c=20201002) and this wasn’t fruitful.
and this wasn’t fruitful.
21 December, 2017 at 12:40 am
Siddhartha Gadgil
Thanks. I did use , but what I did not use was
, but what I did not use was 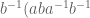 , which I should do. Another change I am making is taking the closure under various symmetries.
, which I should do. Another change I am making is taking the closure under various symmetries.
21 December, 2017 at 4:54 am
Tobias Fritz
Using the inward-repetition technique on powers of the commutator as above, I can also show that![(2k+2)||[x,y]||\leq ||[x,y]^kx|| + ||x^{-1}[x^{-1},y^{-1}]^k||](https://s0.wp.com/latex.php?latex=%282k%2B2%29%7C%7C%5Bx%2Cy%5D%7C%7C%5Cleq+%7C%7C%5Bx%2Cy%5D%5Ekx%7C%7C+%2B+%7C%7Cx%5E%7B-1%7D%5Bx%5E%7B-1%7D%2Cy%5E%7B-1%7D%5D%5Ek%7C%7C&bg=ffffff&fg=545454&s=0&c=20201002) in pretty much the same way.
in pretty much the same way.
Applying this for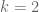 together with
together with ![||[x,y]^2x||\leq 2](https://s0.wp.com/latex.php?latex=%7C%7C%5Bx%2Cy%5D%5E2x%7C%7C%5Cleq+2&bg=ffffff&fg=545454&s=0&c=20201002) , which seems to be the result from above, gives a new best bound of
, which seems to be the result from above, gives a new best bound of ![||[x,y]||\leq\tfrac{2}{3}](https://s0.wp.com/latex.php?latex=%7C%7C%5Bx%2Cy%5D%7C%7C%5Cleq%5Ctfrac%7B2%7D%7B3%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
21 December, 2017 at 6:58 am
Sean Eberhard
Should that be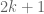 ? (I gather you’re using
? (I gather you’re using ![[x,y]^{2k+1} = [x,y]^k x ([x^{-1}, y^{-1}]^k x^{-1})^{y^{-1}})](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%5E%7B2k%2B1%7D+%3D+%5Bx%2Cy%5D%5Ek+x+%28%5Bx%5E%7B-1%7D%2C+y%5E%7B-1%7D%5D%5Ek+x%5E%7B-1%7D%29%5E%7By%5E%7B-1%7D%7D%29&bg=ffffff&fg=545454&s=0&c=20201002) ?)
?)
21 December, 2017 at 7:19 am
Tobias Fritz
Thank you for checking! What I was using is the inward-repetition method which was extracted by Pace from Siddhartha’s computer calculations. For large , the power
, the power ![[x,y]^n](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%5En&bg=ffffff&fg=545454&s=0&c=20201002) will consist of nestings of
will consist of nestings of
plus a bunch of boundary and centre terms that can be neglected in the limit . Here,
. Here,  is fixed as
is fixed as  varies. It may help to write this out as
varies. It may help to write this out as
in order to see explicitly that each nesting comprises exactly commutator terms. So it seems to me that the
commutator terms. So it seems to me that the  is correct.
is correct.
21 December, 2017 at 7:17 am
Sean Eberhard
Or rather, I can see that![\|[x,y]\|/4 \leq \|[x,y]^k x \|/(4k+3)](https://s0.wp.com/latex.php?latex=%5C%7C%5Bx%2Cy%5D%5C%7C%2F4+%5Cleq+%5C%7C%5Bx%2Cy%5D%5Ek+x+%5C%7C%2F%284k%2B3%29&bg=ffffff&fg=545454&s=0&c=20201002) (assuming wlog that the norm has some basic symmetry, so that we can write the RHS simply). The reason is that a large power of
(assuming wlog that the norm has some basic symmetry, so that we can write the RHS simply). The reason is that a large power of ![[x,y]](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D&bg=ffffff&fg=545454&s=0&c=20201002) can be decomposed into a sequence of expressions of the form
can be decomposed into a sequence of expressions of the form ![([x,y]^k x)^y](https://s0.wp.com/latex.php?latex=%28%5Bx%2Cy%5D%5Ek+x%29%5Ey&bg=ffffff&fg=545454&s=0&c=20201002) or
or ![([x^{-1}, y^{-1}]^k x^{-1})^{y^{-1}}](https://s0.wp.com/latex.php?latex=%28%5Bx%5E%7B-1%7D%2C+y%5E%7B-1%7D%5D%5Ek+x%5E%7B-1%7D%29%5E%7By%5E%7B-1%7D%7D&bg=ffffff&fg=545454&s=0&c=20201002) (plus as you say some small edge effects), and each such term contributes
(plus as you say some small edge effects), and each such term contributes  letters without any cancellation.
letters without any cancellation.
21 December, 2017 at 7:32 am
Tobias Fritz
Aha, that’s interesting, too! It’s slightly weaker and generalizes the bound that I found yesterday to .
.
21 December, 2017 at 9:07 am
Tobias Fritz
[This was a response to a comment of myself that I had deleted. -T]
You also have to repeat the outer conjugation by on the inside, since it’s intended to be part of the repeating pattern. Like that, one nesting of the pattern should correspond to the explicit words on the left and right that I had written down here.
on the inside, since it’s intended to be part of the repeating pattern. Like that, one nesting of the pattern should correspond to the explicit words on the left and right that I had written down here.
Does this clear it up? At least this was the issue that had gotten me confused for a while as I was studying Pace’s considerations.
21 December, 2017 at 4:23 pm
Metrics of linear growth – the solution | What's new
[…] the tradition of “Polymath projects”, the problem posed in the previous two blog posts has now been solved, thanks to the cumulative effect of many small contributions by […]
25 January, 2018 at 10:27 pm
Spontaneous Polymath 14 – A success! | The polymath blog
[…] project, now called polymath 14 that took place over Terry Tao’s blog. A problem was posed by Apoorva Khare was presented and discussed and openly and collectively solved. (And the […]