Since the release of my preprint with Tim, Ben, and Freddie proving the Polynomial Freiman-Ruzsa (PFR) conjecture over , I (together with Yael Dillies and Bhavik Mehta) have started a collaborative project to formalize this argument in the proof assistant language Lean4. It has been less than a week since the project was launched, but it is proceeding quite well, with a significant fraction of the paper already either fully or partially formalized. The project has been greatly assisted by the Blueprint tool of Patrick Massot, which allows one to write a human-readable “blueprint” of the proof that is linked to the Lean formalization; similar blueprints have been used for other projects, such as Scholze’s liquid tensor experiment. For the PFR project, the blueprint can be found here. One feature of the blueprint that I find particularly appealing is the dependency graph that is automatically generated from the blueprint, and can provide a rough snapshot of how far along the formalization has advanced. For PFR, the latest state of the dependency graph can be found here. At the current time of writing, the graph looks like this:

The color coding of the various bubbles (for lemmas) and rectangles (for definitions) is explained in the legend to the dependency graph, but roughly speaking the green bubbles/rectangles represent lemmas or definitions that have been fully formalized, and the blue ones represent lemmas or definitions which are ready to be formalized (their statements, but not proofs, have already been formalized, as well as those of all prerequisite lemmas and proofs). The goal is to get all the bubbles leading up to and including the “pfr” bubble at the bottom colored in green.
In this post I would like to give a quick “tour” of the project, to give a sense of how it operates. If one clicks on the “pfr” bubble at the bottom of the dependency graph, we get the following:

Here, Blueprint is displaying a human-readable form of the PFR statement. This is coming from the corresponding portion of the blueprint, which also comes with a human-readable proof of this statement that relies on other statements in the project:

(I have cropped out the second half of the proof here, as it is not relevant to the discussion.)
Observe that the “pfr” bubble is white, but has a green border. This means that the statement of PFR has been formalized in Lean, but not the proof; and the proof itself is not ready to be formalized, because some of the prerequisites (in particular, “entropy-pfr” (Theorem 6.16)) do not even have their statements formalized yet. If we click on the “Lean” link below the description of PFR in the dependency graph, we are lead to the (auto-generated) Lean documentation for this assertion:

This is what a typical theorem in Lean looks like (after a procedure known as “pretty printing”). There are a number of hypotheses stated before the colon, for instance that is a finite elementary abelian group of order
(this is how we have chosen to formalize the finite field vector spaces
), that
is a non-empty subset of
(the hypothesis that
is non-empty was not stated in the LaTeX version of the conjecture, but we realized it was necessary in the formalization, and will update the LaTeX blueprint shortly to reflect this) with the cardinality of
less than
times the cardinality of
, and the statement after the colon is the conclusion: that
can be contained in the sum
of a subgroup
of
and a set
of cardinality at most
.
The astute reader may notice that the above theorem seems to be missing one or two details, for instance it does not explicitly assert that is a subgroup. This is because the “pretty printing” suppresses some of the information in the actual statement of the theorem, which can be seen by clicking on the “Source” link:

Here we see that is required to have the “type” of an additive subgroup of
. (Lean’s language revolves very strongly around types, but for this tour we will not go into detail into what a type is exactly.) The prominent “sorry” at the bottom of this theorem asserts that a proof is not yet provided for this theorem, but the intention of course is to replace this “sorry” with an actual proof eventually.
Filling in this “sorry” is too hard to do right now, so let’s look for a simpler task to accomplish instead. Here is a simple intermediate lemma “ruzsa-nonneg” that shows up in the proof:

The expression refers to something called the entropic Ruzsa distance between
and
, which is something that is defined elsewhere in the project, but for the current discussion it is not important to know its precise definition, other than that it is a real number. The bubble is blue with a green border, which means that the statement has been formalized, and the proof is ready to be formalized also. The blueprint dependency graph indicates that this lemma can be deduced from just one preceding lemma, called “ruzsa-diff“:

“ruzsa-diff” is also blue and bordered in green, so it has the same current status as “ruzsa-nonneg“: the statement is formalized, and the proof is ready to be formalized also, but the proof has not been written in Lean yet. The quantity , by the way, refers to the Shannon entropy of
, defined elsewhere in the project, but for this discussion we do not need to know its definition, other than to know that it is a real number.
Looking at Lemma 3.11 and Lemma 3.13 it is clear how the former will imply the latter: the quantity is clearly non-negative! (There is a factor of
present in Lemma 3.11, but it can be easily canceled out.) So it should be an easy task to fill in the proof of Lemma 3.13 assuming Lemma 3.11, even if we still don’t know how to prove Lemma 3.11 yet. Let’s first look at the Lean code for each lemma. Lemma 3.11 is formalized as follows:

Again we have a “sorry” to indicate that this lemma does not currently have a proof. The Lean notation (as well as the name of the lemma) differs a little from the LaTeX version for technical reasons that we will not go into here. (Also, the variables are introduced at an earlier stage in the Lean file; again, we will ignore this point for the ensuing discussion.) Meanwhile, Lemma 3.13 is currently formalized as

OK, I’m now going to try to fill in the latter “sorry”. In my local copy of the PFR github repository, I open up the relevant Lean file in my editor (Visual Studio Code, with the lean4 extension) and navigate to the “sorry” of “rdist_nonneg”. The accompanying “Lean infoview” then shows the current state of the Lean proof:

Here we see a number of ambient hypotheses (e.g., that is an additive commutative group, that
is a map from
to
, and so forth; many of these hypotheses are not actually relevant for this particular lemma), and at the bottom we see the goal we wish to prove.
OK, so now I’ll try to prove the claim. This is accomplished by applying a series of “tactics” to transform the goal and/or hypotheses. The first step I’ll do is to put in the factor of that is needed to apply Lemma 3.11. This I will do with the “suffices” tactic, writing in the proof

I now have two goals (and two “sorries”): one to show that implies
, and the other to show that
. (The yellow squiggly underline indicates that this lemma has not been fully proven yet due to the presence of “sorry”s. The dot “.” is a syntactic marker that is useful to separate the two goals from each other, but you can ignore it for this tour.) The Lean tactic “suffices” corresponds, roughly speaking, to the phrase “It suffices to show that …” (or more precisely, “It suffices to show that … . To see this, … . It remains to verify the claim …”) in Mathematical English. For my own education, I wrote a “Lean phrasebook” of further correspondences between lines of Lean code and sentences or phrases in Mathematical English, which can be found here.
Let’s fill in the first “sorry”. The tactic state now looks like this (cropping out some irrelevant hypotheses):

Here I can use a handy tactic “linarith“, which solves any goal that can be derived by linear arithmetic from existing hypotheses:

This works, and now the tactic state reports no goals left to prove on this branch, so we move on to the remaining sorry, in which the goal is now to prove :

Here we will try to invoke Lemma 3.11. I add the following lines of code:

The Lean tactic “have” roughly corresponds to the Mathematical English phrase “We have the statement…” or “We claim the statement…”; like “suffices”, it splits a goal into two subgoals, though in the reversed order to “suffices”.
I again have two subgoals, one to prove the bound (which I will call “h”), and then to deduce the previous goal
from
. For the first, I know I should invoke the lemma “diff_ent_le_rdist” that is encoding Lemma 3.11. One way to do this is to try the tactic “exact?”, which will automatically search to see if the goal can already be deduced immediately from an existing lemma. It reports:

So I try this (by clicking on the suggested code, which automatically pastes it into the right location), and it works, leaving me with the final “sorry”:

The lean tactic “exact” corresponds, roughly speaking, to the Mathematical English phrase “But this is exactly …”.
At this point I should mention that I also have the Github Copilot extension to Visual Studio Code installed. This is an AI which acts as an advanced autocomplete that can suggest possible lines of code as one types. In this case, it offered a suggestion which was almost correct (the second line is what we need, whereas the first is not necessary, and in fact does not even compile in Lean):

In any event, “exact?” worked in this case, so I can ignore the suggestion of Copilot this time (it has been very useful in other cases though). I apply the “exact?” tactic a second time and follow its suggestion to establish the matching bound :

(One can find documention for the “abs_nonneg” method here. Copilot, by the way, was also able to resolve this step, albeit with a slightly different syntax; there are also several other search engines available to locate this method as well, such as Moogle. One of the main purposes of the Lean naming conventions for lemmas, by the way, is to facilitate the location of methods such as “abs_nonneg”, which is easier figure out how to search for than a method named (say) “Lemma 1.2.1”.) To fill in the final “sorry”, I try “exact?” one last time, to figure out how to combine and
to give the desired goal, and it works!

Note that all the squiggly underlines have disappeared, indicating that Lean has accepted this as a valid proof. The documentation for “ge_trans” may be found here. The reader may observe that this method uses the relation rather than the
relation, but in Lean the assertions
and
are “definitionally equal“, allowing tactics such as “exact” to use them interchangeably. “exact le_trans h’ h” would also have worked in this instance.
It is possible to compactify this proof quite a bit by cutting out several intermediate steps (a procedure sometimes known as “code golf“):

And now the proof is done! In the end, it was literally a “one-line proof”, which makes sense given how close Lemma 3.11 and Lemma 3.13 were to each other.
The current version of Blueprint does not automatically verify the proof (even though it does compile in Lean), so we have to manually update the blueprint as well. The LaTeX for Lemma 3.13 currently looks like this:
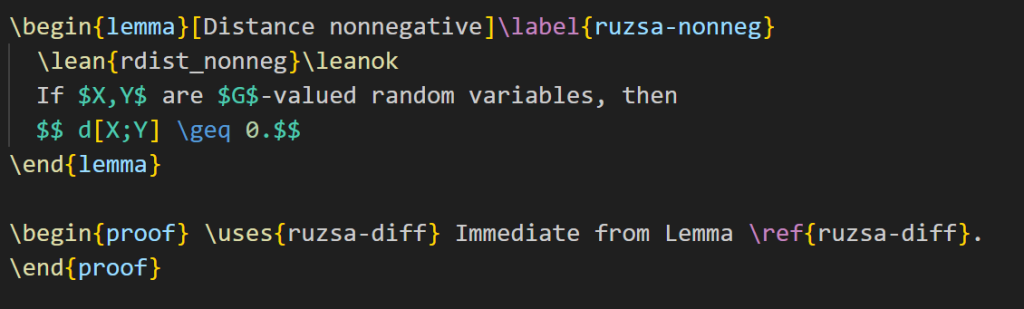
I add the “\leanok” macro to the proof, to flag that the proof has now been formalized:

I then push everything back up to the master Github repository. The blueprint will take quite some time (about half an hour) to rebuild, but eventually it does, and the dependency graph (which Blueprint has for some reason decided to rearrange a bit) now shows “ruzsa-nonneg” in green:

And so the formalization of PFR moves a little bit closer to completion. (Of course, this was a particularly easy lemma to formalize, that I chose to illustrate the process; one can imagine that most other lemmas will take a bit more work.) Note that while “ruzsa-nonneg” is now colored in green, we don’t yet have a full proof of this result, because the lemma “ruzsa-diff” that it relies on is not green. Nevertheless, the proof is locally complete at this point; hopefully at some point in the future, the predecessor results will also be locally proven, at which point this result will be completely proven. Note how this blueprint structure allows one to work on different parts of the proof asynchronously; it is not necessary to wait for earlier stages of the argument to be fully formalized to start working on later stages, although I anticipate a small amount of interaction between different components as we iron out any bugs or slight inaccuracies in the blueprint. (For instance, I am suspecting that we may need to add some measurability hypotheses on the random variables in the above two lemmas to make them completely true, but this is something that should emerge organically as the formalization process continues.)
That concludes the brief tour! If you are interested in learning more about the project, you can follow the Zulip chat stream; you can also download Lean and work on the PFR project yourself, using a local copy of the Github repository and sending pull requests to the master copy if you have managed to fill in one or more of the “sorry”s in the current version (but if you plan to work on anything more large scale than filling in a small lemma, it is good to announce your intention on the Zulip chat to avoid duplication of effort) . (One key advantage of working with a project based around a proof assistant language such as Lean is that it makes large-scale mathematical collaboration possible without necessarily having a pre-established level of trust amongst the collaborators; my fellow repository maintainers and I have already approved several pull requests from contributors that had not previously met, as the code was verified to be correct and we could see that it advanced the project. Conversely, as the above example should hopefully demonstrate, it is possible for a contributor to work on one small corner of the project without necessarily needing to understand all the mathematics that goes into the project as a whole.)
If one just wants to experiment with Lean without going to the effort of downloading it, you can playing try the “Natural Number Game” for a gentle introduction to the language, or the Lean4 playground for an online Lean server. Further resources to learn Lean4 may be found here.

44 comments
Comments feed for this article
18 November, 2023 at 5:02 pm
Anonymous
Wow! Although I don’t understand a word you are saying, it looks very exciting!!
18 November, 2023 at 5:07 pm
Anonymous
Congratulations! This is an extremely important event: A top ranked pure mathematician, in a very short time, has mastered the Lean 4 automated proof checker and applied it to a new result. This is an existence proof for pure mathematicians to routinely codify their proofs in verifiable way, as a part of daily methodology, in the same sense that writing equations in LaTeX has become a standard practice.
18 November, 2023 at 8:14 pm
Anonymous
This tour brought me a lot of joy. Bright days are ahead
18 November, 2023 at 11:38 pm
Anonymous
Thank you so much for writing so well this tour! A lot of this seems natural and one can see how undergraduates can contribute without mastering all the math yet.
19 November, 2023 at 12:00 am
Anonymous
Lean syntax was made flexible to accept people coming over from different programming languages, but it still weirds me out seeing python-esque style with meaningful tabulation over c-style with {brackets}
it always seems so much more convinient to know when one goal has ended and another begins – just find “}”
19 November, 2023 at 12:02 am
Anonymous
same for when definition is over and proof begins – just skip to the “{“
20 November, 2023 at 12:44 am
Anonymous
Haskell-esque, you mean :)
19 November, 2023 at 1:04 am
Formalizations in LEAN – SPP 2026
[…] edit (Nov. 19th): Terence Tao is now also formalizing his recent proof of the Polynomial Freiman-Ruzsa conjecture over F_2: Link. […]
19 November, 2023 at 5:59 am
Anonymous
The blueprint tool was designed and implemented by Patrick Massot. It’s a tremendous contribution; it played an essential role in the sphere eversion project as well as the LTE.
[Reference to Patrick now added to the post, thanks – T.]
19 November, 2023 at 1:17 pm
Anonymous
Your example with the `rdist_nonneg` lemma was really didactic. Not only it provides a simple case to understand how the reasoning can be translated to the Lean 4 syntax, but also showcase how the formalization may be rewritten in a more ‘succinct’ manner.
I have mixed feelings. Although I understand the pros of being able to “script” the proof efficiently (here, in the sense of using less keystrokes), I also feel that a formalization that can be mapped more easily to the original argument would be preferable. On the other hand, if the goal of any formalization is to simply have a digitally verifiable version of the proof, then we should maybe leave the steps of our thought process to the realm of natural language only. Honestly, I don’t actually know were I currently stand in this discussion.
Anyway, thanks for the post. It’s always a joy!
19 November, 2023 at 1:36 pm
Anonymous
It’s a tradeoff. One one hand shorter proofs take less space in the source, making it easier to read the statements and definitions, and can improve checking time.
On the other hand short proofs can be harder to understand for humans.
There are caveats to both. There’s tooling to get readable documentation that hides the proofs, and the utility of human understanding of individual proofs in a proof assistant is limited.
19 November, 2023 at 1:53 pm
Terence Tao
For what it is worth, the compactified proof still translates into Mathematical English in a straightforward, though somewhat ungainly, fashion: “The non-negativity of![d[X; Y]](https://s0.wp.com/latex.php?latex=d%5BX%3B+Y%5D&bg=ffffff&fg=545454&s=0&c=20201002) follows by linear arithmetic from the outcome of transitivity of
follows by linear arithmetic from the outcome of transitivity of 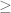 applied to Lemma 3.11 and the non-negativity of the absolute value of
applied to Lemma 3.11 and the non-negativity of the absolute value of ![H[X]-H[Y]](https://s0.wp.com/latex.php?latex=H%5BX%5D-H%5BY%5D&bg=ffffff&fg=545454&s=0&c=20201002) “. In the future I would imagine that the proof would instead look something like `immediate diff_ent_le_dist”, as a translation of “The non-negativity of
“. In the future I would imagine that the proof would instead look something like `immediate diff_ent_le_dist”, as a translation of “The non-negativity of ![d[X;Y]](https://s0.wp.com/latex.php?latex=d%5BX%3BY%5D&bg=ffffff&fg=545454&s=0&c=20201002) is immediate from Lemma 3.11″, although Lean doesn’t quite have the “immediate” tactic coded yet :). [But it is getting there; see for instance the aesop tactic.]
is immediate from Lemma 3.11″, although Lean doesn’t quite have the “immediate” tactic coded yet :). [But it is getting there; see for instance the aesop tactic.]
19 November, 2023 at 2:04 pm
Formalizing the proof of PFR in Lean4 using Blueprint | John's blog
[…] in my feed today: Formalizing the proof of PFR in Lean4 using Blueprint: a short tour by Terence Tao. I would like to learn […]
19 November, 2023 at 4:38 pm
Anonymous
This looks very interesting. However there appears to be no documentation fro blueprint. How did you learn to use it? Did Patrick have to guide you?
20 November, 2023 at 4:17 pm
Terence Tao
It’s mostly Yael Dillies who (rather heroically) got blueprint up and running within the first 48 hours of the project (I believe they may have had some prior experience with an earlier version of the software). It is still in development (I think the correct term may be “beta release”?) but I assume at some point a stable documented version of the software will be available. In the meantime one basically has to ask around on the Lean Zulip for technical support for the software (we reported one minor bug already, so are sort of functioning as “beta testers” for this software).
1 December, 2023 at 5:38 am
Anonymous
Hello Terence! This is my first comment here. Sorry for doing it anonymously.
I admire the breadth of your mathematical interests. I wonder how it is possible to acquire so much knowledge. I think it would be wonderful if you wrote a post about your personal method of study. Do you prefer to thoroughly read one good book on some subject or cursorily read several books on it? Do you read a book once or reread it? Do you always enter every proof or just read statements for the majority of theorems? Or maybe you skip the proofs on the first reading and examine them later?
19 November, 2023 at 10:19 pm
Marton’s “Polynomial Freiman-Ruzsa” Conjecture was Settled by Tim Gowers, Ben Green, Freddie Manners and Terry Tao | Combinatorics and more
[…] of the proof see this post in Terry Tao’s blog. A subsequent post on Terry Tao’s blog describes a project for formalizing the proof using […]
19 November, 2023 at 11:14 pm
Anonymous
mathstodon is full of bloggy bits
1 December, 2023 at 4:49 am
Anonymous
Is it?
2 December, 2023 at 2:22 am
Anonymous
Yes, it’s very bloggy.
20 November, 2023 at 1:12 am
ppalme
Continuous improvement and advancement at it finest. What a wonderful way to plan and document the connections and status of the arguments of a proof. I assume this will be as well applied in hindsight to all the existing proofs or counter-examples in mathematics. Thank you so much for sharing.
23 November, 2023 at 3:54 pm
CPK
Hey Terry, this will be an unrelated question but i was just wondering if you were considering getting into AI research? It looks like we are very close to produce extremely strong AI and the humanity can use your help in handling this challenge.
1 December, 2023 at 5:33 pm
Anonymous
Interesting. I really like the spirit of the project. It seems that lot of aspects could be improved technically, and the most tempting one is to have AI (LLM) write the blueprint pretty much automatically. For this, it needs to come up with a good name for each lemma (they are great at this) , and to understand the dependencies. The real goal is that AI would do the translation to lean, but it is much more challenging.
About the graph, I saw that it uses pygraphviz . I have a feeling the look of this graph could be improved, maybe by using python-igraph.
Eyal
5 December, 2023 at 12:54 am
Terence Tao
The project has now completed its primary goals; the entire dependency graph is now green. More discussion at https://leanprover.zulipchat.com/#narrow/stream/412902-Polynomial-Freiman-Ruzsa-conjecture/topic/Project.20completed!.20.20Thoughts.20and.20reflections.3F
5 December, 2023 at 2:40 pm
Anonymous
So happy to sea this
5 December, 2023 at 11:10 pm
A slightly longer Lean 4 proof tour | What's new
[…] my previous post, I walked through the task of formally deducing one lemma from another in Lean 4. The deduction was […]
6 December, 2023 at 4:07 am
AI颠覆数学研究!陶哲轩借AI破解数学猜想,形式化成功惊呆数学圈 – 比特币中国
[…] Formalizing the proof of PFR in Lean4 using Blueprint: a short tour […]
6 December, 2023 at 7:48 am
Quanta Magazine - Hill News
[…] a mathematician at Paris-Saclay University, to organize the efforts to translate from what Tao called “Mathematical English” into computer code. Blueprint can, among other things, create a chart […]
6 December, 2023 at 11:22 am
F r i e d e r
I’m surprised no one has mentioned how big of a leap this is compared to the vision from 2017 of Thomas Hales of including _fabstract_s in research papers (https://formalabstracts.github.io) which seemed very ambitious at the time. For longer research papers that is still a viable option though, and hopefully may get more traction in the future.
8 December, 2023 at 4:16 am
A a miniature longer Lean 4 proof tour – I NEWS ps
[…] my earlier submit, I walked by the responsibility of formally deducing one lemma from one different in Lean 4. The […]
8 December, 2023 at 3:30 pm
Anonymous
I’m curious: how much did this formalization process increase your confidence in the correctness of the proof?
9 December, 2023 at 6:49 pm
Terence Tao
Well, in this particular case my three coauthors and I proofread the argument multiple times, and in fact also rewrote it multiple times during a process of optimizing the constants, so we already had an unusually high amount of confidence in the argument, and also the argument has a “robust” feel to it, in that even if there was a serious error in one step, this might cause the constants in our final arguments to degrade a bit, but not destroy the result entirely. I guess it did increase to 100% the confidence that the specific exponent of 12 in our final result is rigorously justified. Now we even have a bit of margin of error here, as the exponent was recently improved to 11, and we plan to formalize that argument also.
The formalization did pick up one very minor error in our writeup – one of our lemmas had omitted by mistake the hypothesis that the ambient group be
be 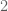 -torsion – but this error caused no damage to the paper as a whole (all the groups we actually need in our argument are 2-torsion).
-torsion – but this error caused no damage to the paper as a whole (all the groups we actually need in our argument are 2-torsion).
12 December, 2023 at 8:46 am
Terence Tao
A small update to the project. While the primary goal of verifying the PFR conjecture is completed, participants expressed interest in continuing the project to formalize some other related results, including (a) an application of PFR to characterize “Approximate homomorphisms”, (b) an application of PFR to obtain a “Weak PFR over the integers”, and (c) a refinement of the PFR constant from 12 to 11. All of these are currently underway (although there was a technical snag with (b), which was that our theory of entropy that we had formalized was restricted to random variables taking values in finite sets, and now we need to extend the theory to random variables taking values in sets such as the integers). One consequence of this is that the blueprint graph may temporarily look a little less than full-green, but one can still check that all the nodes leading up to the original “pfr” bubble are green. And we have an examples file which, when compiled, verifies that the pfr conjecture was established using only the standard type-theoretic axioms of Lean (the axiom of choice, propositional extensionality, and the quotient axiom. [My rough understanding is that these axioms are equivalent to ZFC with universes, though I may be slightly inaccurate on this point.]
14 December, 2023 at 2:27 am
Anonymous
Hi, Prof. Tao, I am curious what is the particular reason to pick this pfr paper to formalize instead of other papers? Are you going to formalize future published papers or it is just an experiment?
16 December, 2023 at 8:35 am
Terence Tao
Partly it was timing; the paper came out soon after I learned the basics of programming in Lean. Partly it was because the paper was relatively elementary, with the main non-trivial mathematical theory required being the theory of Shannon entropy, which was not already in Mathlib (but thanks to the PFR project, there will be thousands of lines of code of lemmas on entropy lemmas, probability kernels, Ruzsa calculus, and related topics that will be ported to Mathlib over the next few months). I was also interested to see how a large scale formalization project operated; the lessons learned from this medium-scale project could help improve larger-scale formalization projects (such as Buzzard’s five-year plan to formalize the proof of Fermat’s last theorem).
At the present level of technology, it is not feasible to formalize every single paper in every single field, but I think it may become realistic to strategically formalize some high profile results in fields that are not built on an immense amount of prior mathematical work (besides the core undergraduate mathematics curriculum, which by now has been largely formalized), or to partially formalize portions of papers (e.g., to formally state, but not prove, the main result, or to formalize a key calculation in the result conditionally on accepting all the other lemmas and cited results in the paper as “black boxes”; this could help gain confidence in the correctness of the paper if the black boxes are all “standard” but the key calculation sensitive to sign errors etc.).
16 December, 2023 at 6:02 am
echolocked
Seems Lean provides a way to fill/check the gaps only when given a well structured blue-prints built by human. Am I missing it or Lean actually provides automatic search for proofs from hypothesis to conclusion?
16 December, 2023 at 8:54 am
Terence Tao
Lean is basically a programming language that is particularly well suited to formal verification tasks. It has some automatic search features (with such names as `apply?`, `exact?`, `hint`, `aesop`, and so forth), but only at very granular levels (it can basically help with suggesting the next tactic to try in a
the next line of code in a formal proof). But there are promising experiments to couple formal verifiers such as Lean with more expressive AI (e.g., GPT), which can propose larger-scale proofs (or proof strategies) which are not guaranteed to work, but which can be tested with the formal verification languages in a feedback loop until a valid proof is obtained. At the current state of technology I think these can handle Lean proofs that require about a dozen lines of code or so, and could perhaps be able to handle problems at the level of an undergraduate math homework problem, but further advances would be needed I think before they can consistently handle something on the level of (say) a Math Olympiad problem, or a graduate math qualifying exam problem.
3 January, 2024 at 6:40 am
Anonymous
In his article “On proof and progress in mathematics”, Thurston said that
In not too many years, I expect that we will have interactive computer programs that can help people compile significant chunks of formally complete and correct mathematics (based on a few perhaps shaky but at least explicit assumptions), and that they will become part of the standard mathematician’s working environment.
How far is Lean 4 from such a goal?
Analysis and algebra in the undergraduate curriculum by now have been largely formalized. The “simi-formal” language students are required to used in their homework are in principle translatable to formal code, and more importantly, the formal code can be translated back to the simi-formal language that human can read.
How about subjects like topology and geometry where even the most “rigorous” arguments often use pictures/figures extensively? Would Lean help in such fields too? Algebraic topology seems to be the only language to go to formalism. Is it feasible to imagine, the formal code could be translated back to the pictorial language that is enlightening for human understanding?
21 January, 2024 at 7:09 pm
Terence Tao
I am not an expert in topology, but for instance sphere eversion has been formalized in Lean: https://leanprover-community.github.io/sphere-eversion/ . Even though the construction is usually presented pictorially, it can be converted to a purely text-based blueprint, which was then formalized.
29 February, 2024 at 6:11 am
A-Team of Math: Unraveling the Critical Link Between Addition and Sets" - Best books shelves
[…] scientist at Paris-Saclay University, to organize the effort to translate the language Tao described as “Mathematical the language of English” in computer […]
3 March, 2024 at 6:11 am
Anonymous
Beautiful work, I have a doubt about this: “Note how this blueprint structure allows one to work on different parts of the proof asynchronously; it is not necessary to wait for earlier stages of the argument to be fully formalized to start working on later stages, although I anticipate a small amount of interaction between different components as we iron out any bugs or slight inaccuracies in the blueprint”. Isn’t it dangerous to prove lemmas that come after without having already proven the lemmas that come before? An error in a previous lemma or in the proof structure that necessitates a different path could make the later proof useless as a different path is needed to achieve the final result.
17 March, 2024 at 6:01 pm
Terence Tao
I have found that as long as the blueprint was written with a reasonable amount of care, and one is guided by good intuition (e.g., coming from motivating examples), this sort of major refactoring does not occur (but if it did, it was a sign that the informal proof was actually not as well understood as people thought, which is also a useful outcome of such a project).
Minor refactoring, on the other hand, has ended up being rather straightforward to achieve in practice – say, adding a hypothesis that some variable has to be non-zero in a lemma (because the proof breaks otherwise), and then making sure that all upstream lemmas then manage to state this non-zero nature. I have found that in Lean, the time taken to refactor an already formalized lemma is significantly faster than the time taken to formalize the lemma in the first place, and in fact in some cases such a formal refactoring was faster than what a human refactoring would be. For instance, there was a point where a constant 12 improved to a constant 11 in one theorem, and hundreds of lines of downstream code then had to be refactored to reflect this update. With a standard LaTeX writeup this would be a rather tedious and error prone process: but with Lean, one can simply replace 12 with 11 in the theorem, and the compiler will then dutifully point out the dozen or so lines that now do not compile properly, which can then be quickly adjusted with a number of spot fixes without having to do any of the tedious line-by-line checking one would do in a human refactoring.
4 April, 2024 at 2:06 pm
Marton’s conjecture in abelian groups with bounded torsion | What's new
[…] still open. The result has been formalized in the proof assistant language Lean, as discussed in this previous blog post. As a consequence of this result, many of the applications of the previous theorem may now be […]
15 April, 2024 at 2:02 am
Theorem Proving using Machine Learning – Lean 4 – A Guide To Mathematical Studies
[…] Formalizing the proof of PFR in Lean4 using Blueprint: a short tour A slightly longer Lean 4 proof tour […]