Last updated: Feb 24, 2024
Hardback, 530 pages (ISBN-13: 9780521853866; ISBN-10: 0521853869)
Paperback, 512 pages (ISBN-13: 9780521136563)
This book covers the basic tools in additive combinatorics: sum set estimates, inverse theorems, graph theory techniques, crossing numbers, algebraic methods, Szemerédi’s theorem.
- Sample chapters (contents, probabilistic method, sum set estimates, additive geometry)
— Deleted scenes —
— Precursor material —
- Gowers’ proof of Szemeredi’s theorem for progressions of length 4
- Non-commutative sum set estimates
- The Roth-Bourgain theorem
- Math 254A (some highlights of arithmetic combinatorics)
- Math 262 (Topics in Combinatorics)
— Errata —
- p. xi: Reference [116] should be [113].
- p. xiv: “Chevalley-Waring” should be “Chevalley-Warning”.
- p. 1, last display:
should be
.
- p. 3, after Lemma 1.2: “with probability n” should be “with probability 1”.
- p. 4, after Question 1.4, “Kleiman” should be “Kleitman”.
- p. 5: In Q. 1.1.3,
should be
(two occurrences). In Q. 1.1.5,
and
should be
and
respectively.
- p. 6: Exercise 1.1.8 is missing. This exercise reads: “Let
be an additive set. Show that there exists a subset
of cardinality
such that
. (Hint: translate
randomly by independent elements of
, and use the first moment method.)”
- p. 8: In the fourth display,
should be
.
should be
.
- p. 9: In Exercise 1.2.4, the inequality should be reversed.
- p. 11: In the paragraph after (1.17),
should be
.
- p. 14: In the 9th line from below,
should be
(two places); similarly before (1.23) on P. 15. In the final display,
should be
(not
as stated previously).
- p. 15: In the first display, the first
sign should be
.
- p. 17: In the first line, Corollary 1.8 should be Corollary 1.9. In Exercise 1.3.1, n needs to be even and
needs to be odd. In Exercise 1.3.4, the first expectation should be a probability. In Exercises 1.3.5 and 1.3.6,
needs to be positive.
- p.18: In Exercise 1.3.8, the expectation should be
and the variance should be
. In Exercise 1.3.11,
should be
.
- p. 21: In Definition 1.21,”we say that
is a
-complementary base of
” should be”we say that
is a
-complementary base of order
of
“.
- p. 22, before second display: Lemma 1.53 should be Theorem 1.53.
- p. 23: Near top: “the event that
is good” should be “the event that
is good”. In the last line of the proof of Lemma 1.24,
should be
.
- p. 24: In the last display, the third
should be
.
- p. 25: In the first display,
should be
.
- p. 36: In the first line of the proof of Theorem 1.39, add “Without loss of generality we may assume
. In the third display on the last line,
should be
.
- p. 37: In the first display,
should be |A|.
- p. 38: In the RHS of the display in Corollary 1.42 RHS of the formula,
should be
.
- p. 40: In the RHS of the last display
should be
.
- p. 41: In the first display,
should be
.
- p. 44: One line before the third display,
should be
.
- p. 47: In the penultimate equation in the proof of Proposition 1.51, the summation
should be
, and one should observe that the integrand vanishes for
. In the last equation,
should be
. The last sentence of the proof should then say “Direct computation then shows that
and
, and the claim follows”.
- p. 57: In the bounds for
,
should be
(two occurrences). Similarly,
should be
(two occurrences).
- p. 58: In Exercise 2.2.5,
should be
.
- p. 68: In Exercise 2.3.14,
should be
, and
should be
. Replace “though the set
may be symmetric around a non-zero origin
” with “where by symmetry here we mean that
”. (The point is that
might not actually exist and be unique for some groups.)
- p. 69: In Exercise 2.3.20, a square root is missing from the left-hand side.
- p. 76: In Exercise 2.4.4, Corollary 2.19 should be Corollary 2.20.
- p. 77: In Exercise 2.4.7,
should be
.
- p. 78: In, Exercise 2.4.11, Proposition 2.4.11 should be Proposition 2.27.
- p. 79: In (2.20),
should be
.
- p. 80: In the first paragraph,
should be
. In the second display of the proof of Lemma 2.30, the \frac{}{} should be a / (and in particular should not enclose the left-hand side of the inequality). Near top: “the iterated sum and difference sets of
and
” should be the iterated sum and difference sets of
and
“.
- p. 82: In Exercise 2.5.3, add
after
. In Exercise 2.5.4, “is can be used” should be “can be used”.
- p. 85: In, Lemma 2.23, “there exists a set
” should be “there exists a set
“.
- p. 86: In the first display of the proof of Lemma 2.34,
should be G.
- p. 87: In the fourth display, the
on the LHS and RHS should be
. In the last sentence in the statement of Theorem 2.35,
should be
.
- p. 95: Lemma 2.41, while correct, does not imply Corollary 2.42 as stated (since
does not control
). Thanks to Mei-Chu Chang for pointing out the problem. Replace “As
, this implies” by “A similar argument (see [Proposition 4.5, 362]) gives”. Rename Corollary 2.42 as Proposition 2.42, replace “
” by “
” in the first sentence, replace “
” by “
” in the second sentence, and replace “
” by “
” in the display.
- p. 96: “verstion” should be “version”.
- p. 97: In Theorem 2.48 (ii),
should be
.
- p. 107: before Corollary 2.62, “Corollary 2.60” should be “Theorem 2.60”.
- p. 112, bottom: “in Section 4.4” should be “to Section 4.4”.
- p. 114, line 3: the last
should be an
.
- p. 115, fourth line of Lemma 3.4:
should be
.
- p. 116, proof of Corollary 3.6: “induce” should be “induct”. In the last two sentences of this proof,
should be
(three occurrences).
- p. 117, proof of Theorem 3.7: “induce” should be “induct”.
- p. 118: Exercise 3.1.1
should be
- p. 120: In the second display,
should be
.
- p. 121, after the proof of Lemma 3.11, “an progression” should be “a progression”.
- p. 122, after first display: “for all real
” should be “for all non-negative reals
“. In the next sentence, “for any integer
” should be “for any positive integer
“, and “
” should be “
“.
- p. 123, proof of Theorem 3.13:
should be
. On the same line, “whch” should be “which”.
- p. 124:
should be
(two occurrences). In the first display and two lines further down,
should be
. In the second-to-last display,
should be
. In the last paragraph,
should be
.
- p. 128: In the proof of Proposition 3.19,
should be
. In the next paragraph, the inclusion
should be
, and the constraint
may be relaxed to
.
- p. 129: In the proof of Proposition 3.20, “induce” should be “induct”. Remove the “that” before “(using Fatou’s lemma)”. In the next display,
should be
.
- p. 130: In Exercise 3.4.5, “amd” should be “and”. In Exercise 3.4.6, all occurrences of
should be
.
- p. 131: Delete the sentence beginning with “The lower bound is trivial…” from the proof of Lemma 3.21.
- Page 132: In the statement of Lemma 3.24, one needs to add the hypothesis that all the sums in
are distinct.
- p. 133: On the second display,
should be
. Just before the third display,
should be
. In Corollary 3.25,
should be
. In the next display, delete
.
- p. 134: In Lemma 3.27, Blichtfeld should be Blichfeldt.
- p. 139: In the last display, |B| should be
.
- p. 140: In the proof of Theorem 3.34,
should be
.
- p. 141-142: Throughout the statement and proof of Lemma 3.36,
should be replaced with
, and
replaced with
. In the last two equations in the display, replace
and
both by
.
- p. 144: In the last pragraph of the proof of Theorem 3.38, the superfluous ) should be deleted.
- p. 145: In Theorem 3.40, replace “If
and
is not proper” with “If
,
is not proper, and
is torsion-free”. In the proof, “We induce on
” should be “We induct on
”. On the last line, “unless
is torsion-free” should be deleted.
- p. 147: In the second paragraph, “
” should be “
“.
- p. 155: In Q 4.1.7,
should be
. In Q 4.1.10, the range of
should be
rather than C.
- p. 157: In (4.14),
should be
.
- p. 158: In the proof of Lemma 4.10,
should be
. Between the second-to-last and third-to-last lines of the long display in that proof, insert the lines “
” and “
”.
- p. 159: In Exercise 4.2.2, “let
the dual exponent” should be “let
be the dual exponent”.
- p. 162: In the proof of Lemma 4.14,
should be
. In the third line of Corollary 4.15,
should belong to
rather than
, and
should be
. (Remark: the order estimate only gives the qualitative result
for
sufficiently large, but the small values of
can be done by hand.) In the last word of the last sentence,
should be
.
- p. 164, in Q. 4.3.10, “
” should be “
“.
- p. 165, bottom paragraph: “combinatorialinformation” should be “combinatorial information”.
- p. 170, proof of Lemma 4.25:
should be 2, and the condition
should be
.
- p. 171, in Q 4.4.6,
should be
.
- p. 173: In the proof of Proposition 4.29, (4.31) should be (4.30). In the second and last displays,
should be
.
- p. 174: In the third display,
should be
.
- p. 175: In the four summations involving
,
should range over Z rather than S. After the second display,
and
should be
and
respectively, and similarly on the third display.
- p. 176: In the last display,
should be
.
- p. 177: In the first display,
should be
. In the third display,
should be
. In the penultimate display,
should be
. “If take” should be “Taking”. In the last display,
should be =.
- p. 179: In Exercise 4.5.4,
should be
.
- p. 181: In the proof of Lemma 4.35, “incrementing k+1” should be “incrementing k”.
- p. 182, middle: “
” should be “
“. After the fourth display,
should be
. In the last display, the upper limit of the integral should be infinite.
- p. 183: In the last four displayed equations, all
signs should be
. In (4.38),
is missing from the RHS. In the sixth display,
should be
.
- p. 184: In the fourth and fifth displays,
should appear on the right-hand side. (Also, to avoid ambiguity, one may wish to rewrite
in the fifth display as
.)
- p. 185: In the proof of Proposition 4.39,
should be
.
- p. 186: In Proposition 4.40,
can be improved to
(though the existing bound is certainly correct). In the line before the last display,
should be
.
- p. 187: In Theorem 4.41,
should be
.
- p. 190: In the first display, 1/2 should be 1/6.
- p. 191: The second equality in the third line should be an inequality
.
- p. 193: In the third line of the first display,
should be
. In the second and final displays (and in the first display of p194 and the second, third, and fourth displays in p195),
should be
(seven occurrences).
- p. 194: In the first display,
should be
. After the second display,
should equal latex \delta^2$ rather than
.
- p. 195, first line:
should be
. In the first display,
should be M.
- p. 196: After the proof of Theorem 4.47, “, non-empty set E” should be “. One then considers a non-empty set E”. A few lines afterwards, “replace” should be “replaces”. In Exercise 4.7.1,
should be
.
- p. 200: “induce” should be “induct” (four occurrences). In the fourth line of the proof,
should be
.
- p. 203: the subscript
should be
(three occurrences).
- p. 208: In the sixth line of the last display,
should be replaced by
(here we use the bound
), and similarly for the seventh through ninth lines (and the tenth line should be deleted). [Update: this is slightly inaccurate, see revised erratum below.]
- p. 209: In Exercise 5.1.2, Lemma 5.1 should be Lemma 5.2. In Exercise 5.1.6, “Schirelmann” should be “Schnirelmann”.
- p. 210: In Exercise 5.1.9,
should equal
rather than p.
- p. 211: In the proof of Lemma 5.13, “induce” should be “induct” (two occurrences). “Frieman” should be “Freiman”.
- p. 212: In the proof of Lemma 5.14,
should be
.
- p. 213: In the proof of Proposition 5.15,
should be
,
should be
, and
should be
.
- p. 214: In the proof of Corollary 5.16, “induce” should be “induct”.
- p. 215, middle, “closed unit interval” should be “closed unit ball”. In the proof of Lemma 5.18, “induce” should be “induct”.
- p. 216, middle: “some origin
” should be “we see that
contains a set
symmetric around some origin
“.
- p. 217: In the first paragraph, P’ should be symmetric around a rather than around a’. In the proof of Theorem 5.20, “induce” should be “induct”.
- p. 218, fourth line:
should be
. Similarly on the sixth line. Also, on that line,
should be
.
- p. 219: Before the third display, (5.14) should be (5.13).
- p. 221: In the first example,
should be
. In the fourth line of the fifth example,
should be
.
- p. 225: In the first line,
should be
. A period is missing before “Fortunately” in the sentence after the first display.
- p. 226: In Exercise 5.3.7, the range of
should be
rather than
.
- p. 229: In the proof of Theorem 5.30, Corollary 2.23 should be Lemma 5.26. In the last line of this proof, P should be Frieman isomorphic to Q, rather than to P. In Lemma 5.31,
should be
.
- p. 230: In the first display,
should be
. In the second display,
should be
.
- p. 231: In the fifth line,
should be
. In Theorem 5.33, the hypothesis
should be included, and the first paragraph of the proof of Theorem 5.33 should be deleted. Throughout this proof,
should be
.
- p. 236: In Proposition 5.41, “Frieman” should be “Freiman”. In Corollary 5.42, K should be d.
- p. 237: In Exercise 5.5.1, Hom should be
.
- p. 240: In Theorem 5.44, “Then there a” should be “Then there is a”
- p. 241: The end of proof box on the fourth line should be moved to the end of the first paragraph in page 244.
- p. 243: In the last line,
should be
.
- p. 247: In Exercise 6.1.2, “symmetruc” should be “symmetric”, and one should assume
.
- p. 248: In Exercise 6.1.4, the denominator
should be
.
- p. 249: In the second line from the bottom, Ruzsa[297] should be Ruzsa[303].
- p. 250: In the first display,
should be r (and in the previous line,
should have radius
rather than r).
- p. 253: In Remark 6.8, “We say that S” should be “We say that S is”.
- p. 255: In the proof of Theorem 6.9, “induce” should be “induct”, “vacuoust” should be “vacuous”, and “(with
)” should be deleted. “
” should be “
“. Shortly afterwards, “latter” should be “former”.
- p. 256: In the proof of Corollary 6.12, “induce” should be “induct”, and “
contains a” should be “
contains an” (two occurrences). “complete the induction and than the proof” should be “closes the induction and completes the proof”.
- p. 257: In the first line, “
monochromatic” should be “
-monochromatic”. In Theorem 6.15,
should be
. In Proposition 6.16,
should be
, “exists distinct classes” should be “exist distinct classes”, and “
” should be “non-zero
“. In the proof of Proposition 6.16, “induce” should be “induct”, and “inducing” should be “inducting”.
- p. 258: In the last paragraph of the proof of Proposition 6.16,
should be
.
- p. 259, first paragraph: “the bound…which follow…are” should be “the bound…which follows…is”. “being of growing” should be “growing”.
- p. 260, in Exercise 6.3.3,
should be
.
- p. 263: In the statement of Corollary 6.20, the
in the denominator in the last line should be
. In the second paragraph of the proof. the denominator
should be
.
- p. 264: In the second paragraph, the denominator
should be
. In the penultimate display,
should be
. In the proof of Corollary 6.20,
should be
(two occurrences), and
should be
(one occurrence). In the proof of Theorem 2.29,
should be
(four occurrences).
- p. 265: In Theorem 6.21, the first “then” should be an “and”. In the third display,
should be
.
- p. 268: In the first line, “smallest” should be “largest”. In the line before Example 6.26, the right parenthesis should be deleted. In the fifth paragraph,
should be
.
- p. 271: In the last paragraph of 6.5.2,
should be
(two occurrences).
- p. 272, first display:
should be
.
- p. 276: In the first bullet point, “can occur” should be “is”. In the second sentence after these bullet points, “has” should be “have”.
- p. 278: In the proof of Corollary 7.4,
should be
. In the proof of Lemma 7.6, “induce” should be “induct”.
- p. 279: In the third paragraph, Theorem 6.31 should be Theorem 6.32.
- p. 280: In Exercise 7.1.4, Proposition 7.9 should be Lemma 7.9. In Exercise 7.1.1, Lemma 7.3 should be Lemma 7.2.
- p. 286: In the first display, there should be no m on the LHS.
- p. 289: In the third line,
should be
.
- p. 290: In the display before (7.4),
should be
.
- p. 292: In Exercise 7.3.2,
should be
.
- p. 294: In statement of Proposition 7.21, add “Furthermore, each of the
lies in the set
“.
- p. 295: After the third display, the
s should be
s.
- p. 298: In the last paragraph,
should be
.
- p. 300: In the fourth line of the proof of Corollary 7.28,
should be
(two occurrences).
- p. 308: In the third paragraph, Andrew’s should be Andrews’.
- p. 309: In the second paragraph, the accent on Szemerédi is misplaced. The proof of Theorem 8.1 (as well as the explicit choice of constants) is due to Chazelle, Sharir, and Welzl (see M. Aigner and G. Ziegler, Proofs from the Book, Springer-Verlag,
Heidelberg, (2004), viii+239 pp.) - p. 310: In the second display,
should be
.
- p. 312: In the dual formulation of Corollary 8.5, there is a “:” missing in the set notation.
- p. 314: In Ex 8.2.6, “exactly two points” should be “at least two points”. (It is however an interesting question as to whether the exercise is correct as stated.) In Exercise 8.2.10, a-a should be a-a’.
- p. 316: In Theorem 8.15,
should be
(two occurrences).
- p. 318: On the sixth line, a right parenthesis is missing in
. In Exercise 8.3.4,
should be
. In Exercise 8.3.5,
should be
.
- p. 322: In (8.6)
should be
.
- p. 324: In Exercise 8.4.3,
should be
.
- p. 325: Exercise 8.4.7 is heuristically correct, but the rigorous implementation of this exercise is somewhat subtle; see this post for details.
- p. 330: In the proof of Theorem 9.2, “induce” should be “induct”.
- p. 331: After the end of the proof, “Combinatorial Nullstelensatz” should be “combinatorial Nullstellensatz”.
- p. 332: In Exercise 9.1.2, the
in
should be
. In Exercise 9.1.3, the Hilbert nullstellensatz of course only applies when F is algebraically closed. In Exercise 9.1.4,
should be
.
- p. 333: In Lemma 9.3,
should be
.
- p. 338: In the proof of Theorem 9.11, “induce” should be “induct”.
- p. 341: In Question 9.2.6,
should be
.
- p. 342: In Theorem 9.17,
should be
, and
should be
. In the last sentence of the proof of Theorem 9.16, “
” should be “
“.
- p. 343: In the first display, the right-hand side should just be
. In the next paragraph,
should be
, and in the paragraph after that,
should be
. In the first line of the last display,
should be
. In Lemma 9.18, the second sentence should start “Then” rather than “The”. In the 5th line (the line before 2nd display)
should be
.
- p. 344: In proof of Corollary 9.19, “the multiplicatively invertible” should be “the set of multiplicatively invertible”. After the end of the proof of Lemma 9.18, “additive group” should be “an additive group”. In Theorem 9.20, “be power of
” should be “be a power of
“.
- p. 345: In Exercise 9.3.3, “Let
” should be “Set
“, and
should be
.
- p. 348: In the proof of Theorem 9.24,
should be
.
- p. 350: In Lemma 9.27,
should be
.
- p. 352-353: In the proof of Lemma 9.31: all occurrences of
should be
, etc. Also,
should be
. In Theorem 9.32, [266] should be [267]. In Exercise 9.5.3,
should be
.
- p. 354: Right before Theorem 9.36, “made a significant progress” should be “made significant progress”. In the third line of Exercise 9.5.4,
should be
. In the RHS of (9.14),
should be
. Right after Theorem 9.36,
should be
.
- p. 355: In Remark 9.38, “combining” should be “combined”. In the first display,
should be
. In the last sentence of the proof of Theorem 9.36,
should be
.
- p. 356: In Exercise 9.6.3,
should be
, and “induce” should be “induct”.
- p. 358: In the 3rd display
should be
.
- p. 362, bottom line: “as follows” should be “are as follows”.
- p. 363, middle: delete “and using Exercise 9.4.1”. Somewhat further down,
should just be
.
- p. 364, in the proof of Lemma 9.48, “least common multiple” should be “greatest common divisor”.
- p. 365: In Theorem 9.5.2, add the condition “
is nonzero”.
- p. 366: In the last line of the proof of Theorem 9.53, max should be min. In the first paragraph of the proof of Corollary 9.54, “keeping
fixed” should be “keeping
fixed”.
- p. 367: In Exercise 9.8.3
should be
(two occurrences).
- p. 368: In Exercise 9.8.8, delete “, and let
be distinct integers in
“. In the second display of Exercise 9.8.11, the sup should be an inf.
- p. 370: In Examples 10.3,
should be
. In Theorem 10.5, the phrase “… with
coprime to
” should be added at the end of the first sentence.
- p. 371: In Exercise 10.0.4, Exercise 6.3.7 should be Theorem 6.17. In the third line of Exercise 10.0.5, “color class” should be “color classes”.
- p. 375: In the second and third displays,
should be
. In the line afterwards, (4.3) should be (4.2).
- p. 376: In the second line before the exercises, one of the “that”s should be removed.
- p. 377: In Exercise 10.1.6, “aproper” should be “a proper”.
- p. 378: Corollary 10.10 should be Proposition 10.10, and similarly in page 380.
- p. 379: In the third display of the proof of Lemma 10.15,
should be
. In the third line of the proof of Theorem 10.12 (which should be Proposition 10.12),
should be
. In the second line of the proof of Theorem 10.12, “induce” should be “induct”.
- p. 380: In the proof of Proposition 10.17, “induce” should be “induct”. In the line after the top display, it should say “
” rather than “
“.
- p. 381: In the second line,
should be
. (In the next two displays, the 4 is correct.) In the third line, add “and
in
” just before “, such that”. In the third and fourth displays,
should be
.
- p. 382: in the paragraph after statement of Theorem 10.20: replace”
and
” with just “
“.
- p. 383: in the third display, the first = sign should be
, while
should be
|.
- p. 384: in Lemma 10.22,
needs to be between 0 and 1.
- p. 385: in third display,
should be
, and similarly on the next two lines. In the next display, the sum
should be enclosed in parentheses.
- p. 386: Exercise 10.2.1 is redundant (being essentially the union of 10.0.8 and 10.0.11) and should be deleted.
- p. 387: In the first line, Theorem 10.12 should be Proposition 10.12; in the fourth line, Corollary 10.10 should be Proposition 10.10.
- p. 388, fifth line of proof of Lemma 10.25: insert “, since” after “On the other hand”. In the third-to-last line, “the sum” should be “the summand”.
- p. 389: in top line, “
is bounded” should be “
is bounded by 1″. In third line,
should be
. In Exercise 10.3.1, add the hint “(You may want to first establish the weaker but easier bound
.)”
- p. 390: In Proposition 10.28, one should have
rather than
.
- p. 391: The conclusion of Lemma 10.29 should be
rather than
(one wants a density increment, not a density decrement). To get this, one has to add “also, observe that the expression inside the norm has mean zero” just before the final display, replace the
norm on the final display with a supremum (with no absolute values), and remove the absolute values on the first display of the next page.
- p. 394: In the second, third, and fourth display, the indicator functions should be applied to x instead of r. Also, in the fourth equation,
should be
.
- p. 398: About half-way down on the page, “to be introduce” should be “to be introduced”.
- p. 402: in the last two displays,
should be
.
- p. 407: In Remark 10.44, “Gowers shown” should be “Gowers has shown”.
- p. 418: In “choices of
“, the parenthesis should be deleted.
- p. 439: In the second line,
should be
. In the fourth line,
should be
. In the proof of Proposition 11.12, “induce” should be “induct”.
- p. 454: In the line before Theorem 11.27, the brackets \{ \} around
are missing.
- p. 462: In the last line, “in” should be
.
- p. 465: “and some k-pseudorandom measure
, then” should be “for some k-pseudorandom measure
. Then”.
- p. 474: In the proof of Lemma 12.6, “induce” should be “induct”. In Theorem 12.5, “constants” should be “constant”.
- p. 500: In [288], “arithemtic” should be “arithmetic”.
- p. 503: Reference [352] should be redirected to [380].
- p. 505:
should be
, and O(f(n)) needs to be in math mode.
- p. 506: “Chevalley-Waring” should be “Chevalley-Warning”, and Blichtfeld should be Blichfeldt.
— Errata to the revised edition —
- p.6. In Exercises 1.1.6, 1.1.7,
should be
.
- p. 7: in the display after (1.10), add an additional right parenthesis before the equality sign.
- p. 12. In Example 1.12, “Legendre’s theorem” should be “Lagrange’s theorem”.
- p. 15. In the final display,
(or
) should be
(this supersedes the previous erratum for this line).
- p. 16. In the final display,
should be
. On the next line, “Corollary 1.10 (or Corollary 1.8)” should read “Corollary 1.9”.
- p.17. In Exercise 1.3.4,
should be
. Also add “The variance of a complex variable
is defined to be
.
- p.18. In Exercise 1.3.10, add “with
not both equal to
” before the first comma.
- p. 23: In (1.30), third summation,
should be
.
- p. 26: In the penultimate paragraph,
should be
.
- p. 30. In the third display,
should be
(say), and the third equality should be a
sign.
- p. 35, first line: a right parenthesis ) missing before
.
- p. 36-37: The proof of Theorem 1.39 requires a number of significant changes. After the first paragraph, add “We will show first that with probability 1, that any natural number
has at most a bounded number of representations as the sum of
elements of
between
and
; the treatment of the remaining sums in which at least one term is less than
is left as an exercise.” Then, in the definition of
and also in the computation of
, insert the lower bound
in the sum. On the first line of page 37, and in Exercise 1.7.2, replace
with
for some
. Extend Exercise 1.7.2 by adding “Then complete the proof of Theorem 1.39 by using similar arguments to treat the contribution of sums in which some of the summands have size less than
for some sufficiently small
, by using an induction hypothesis to bound the number of representations by sums of fewer than
elements of size less than
.”
- p. 42: Exercise 1.8.1 contains a number of inaccuracies (namely, “
” should be “
, and “no two elements” should be “no two distinct elements” (and so
should really be
here)), and is in any case a consequence of Theorem 6.2, and so should probably be deleted (it is rather difficult to establish this exercise with the tools developed up to that point).
- p. 45: After equation (1.45), the assertion
should instead be
, where
is the logarithmic integral.
- p. 48: in the first bound of Exercise 1.10.3, the error term of
should be
.
- p.54: After the proof of Lemma 2.1, “Corollary 5.13” should be “Lemma 5.13”.
- p. 58: In Exercise 2.2.6,
should be
. (This error is not present in the first edition.)
- Page 61. In the penultimate bullet point of Proposition 2.7, add the requirement
. After Proposition 2.7, “
,
, or
respectively” should be “
,
, or
respectively”.
- p.62: In (2.7), after Definition 2.8,
should be
.
- p. 63: In the sixth line of the first display,
should be
.
- p. 66: In Exercise 2.3.2,
should be
. In Exercise 2.3.7, replace the first bound with
and the second bound with
.
- p. 70: In the statement of Ruzsa’s covering lemma, insert “at most” after “In particular,
can be covered by”.
- p. 71: In the proof of the Green-Ruzsa covering lemma, “the size of
” should be “the size
of
“.
- p. 73: In Corollary 2.22, replace “covered by
” with “covered by at most
“. Similarly in the proof of the corollary.
- p. 74: In Corollary 2.23, add the hypothesis
, and replace the exponent
by
.
- p. 76: In Exercise 2.4.5,
can be improved to
. In the final inequality in Exercise 2.4.8, the quantities
and
should be swapped.
- p. 83: In Exercise 2.5.5, the small K case is somewhat more difficult than the hint suggests, since if
for some small
then a direct application of Exercise 2.5.4 will give losses of
rather than
. One way to proceed is to first use the lossy argument, apply Exercise 2.4.4 to locate a relevant finite group, and then use ad hoc arguments to refine the error. In Exercises 2.5.6 and 2.5.7, the reference [80] should instead be to “G. Elekes, I. Ruzsa, The structure of sets with few sums along a graph”, J. Combin. Theory Ser. A 113 (2006), no. 7, 1476–1500. Finally, in Exercise 2.5.7, the graph G should be assumed to be symmetric.
- p. 88: In the definition of
,
should be
.
- p. ???: Exercise 2.6.6 is false as stated; the conclusion needs to be weakened, in that the indicated translates of
only cover
of
rather than all of
. Furthermore, the proof requires Exercise 6.5.1. Hence this exercise should be moved to Section 6.5, with a hint to use Exercise 6.5.1 and the Ruzsa covering lemma (Theorem 2.35 is not directly required, though the strategy of proof can still be useful).
- p. 100: In Corollary 2.52, A should be assumed to be a finite subset, rather than a finite subfield.
- p. 104: the last paragraph here (from “Now let
…” onwards) can be deleted, and replaced by the much shorter “Since
and
contains both 0 and 1, we have
“.
- p. 116: In the proof of Corollary 3.6,
should be
, and “for some
” should be “for some
.
- p. 118: In the proof of Corollary 3.9, some explanation should be added as to why the torsion group is finite. This follows first from the observation that any subgroup of a finitely generated abelian group is also finitely generated (this follows from viewing the group as the image of a lattice and using Lemma 3.4), and that finitely generated abelian torsion groups are finite (because there are only finitely many distinct ways to combine the generators together).
- p. 121: After Lemma 3.11, “exponentially in |A|” should be “exponentially in K”.
- p. 128: In the proof of 3.19, the normalisation
should not be used; instead, one should normalise
(and the comment that it suffices to show
should be deleted). The second display should then be restricted to the range
(note that Lemma 3.18 requires all sets involved to be non-empty), and one should also mention the weighted arithmetic mean-geometric mean inequality at the end of the proof.
- p. 131: In the second paragraph of the proof of Lemma 3.21, “translates of
” should be “translates of
“.
- p. 132: In Lemma 3.23, the hypothesis that the cosets
for
are disjoint should be added.
- p. 133: The Kronecker approximation theorem should more accurately be called a simultaneous Dirichlet approximation theorem.
- p. 134: In the first line, “with” should be “within”.
- p. 135: In the definition of
,
should be
.
- p. 136, in the first line, “directional basis for A” should be “directional basis for B”.
- p. 142: In the proof of Lemma 3.36,
and
should be
and
respectively (for consistency).
- p. 143?: Exercise 3.5.3 is false. In its place, one can put the following example (from this reference): Let
be the convex hull of the four points
for a natural number
. Show that
has cardinality
, but
has cardinality at least
. Thus one cannot remove the symmetry hypotheses from Lemma 3.21.
- p. 154: In display (4.9) there is a full stop missing.
- p. 155: In Exercise 4.1.5, “pairwise independent” should be “pairwise uncorrelated”. In Exercise 4.1.7,
should be
. In Exercise 4.1.8,
should be
. In Exercise 4.1.4, “for all
” should be “for all
“.
- p. 156: In the second display (defining
),
should be
.
- p. 158: In the proof of Lemma 4.10, in the final display, the last equals sign should be a
sign. An additional sentence of explanation should be added: “The penultimate inequality follows from Plancherel’s theorem, followed by Minkowski’s inequality to estimate the
norm of f.”
- p. 162: In the last line, “sum of two elements” should be “sum of two squares”.
- p. 163: In Exercise 4.3.4, “is contained in a coset” should read “is a coset”. In Exercise 4.3.14, Polya should be Pólya (and similarly for the corresponding entry in the index). In Exercise 4.3.2,
should be
. In the discussion of Lemma 4.16,the term
in the approximation for
after the display should be deleted. In the statement of Lemma 4.16,
should be
.
- p. 165: In Exercise 4.3.15, the transformation
needs to be assumed to be symmetric.
- p. 166: In Lemma 4.20, the additional hypothesis
should be added.
- p. 168-169: Before Proposition 4.23, “dispense with” should be “almost dispense with”. In Proposition 4.23, the proper progression
should be the proper coset progression
, where
is a subgroup of
(i.e. the multiples of
for some factor
of
). The last sentence of the proposition is redundant and can be deleted. In the proof, one first handles the case when
has order
in
, in which case the first display of p.169 is an equality, and one obtains a progression of rank
. In the general case, when
has order
for some
dividing
, one then passes from
to
by quotienting out the group
generated by
, and then applies the previous case.
- p. 170: In the proof of Lemma 4.25, “find thus find” should be “thus find”.
- p. 171: In Exercise 4.4.7, “lower” should be “increase”.
- p. 174: In Remark 4.31, the sentence “The converse statement is true up to logarithmic factors; see exercises.” should be deleted.
- p. 176-177: The denominator
in (4.34) can be improved to
, by setting
equal to
instead of
in page 177 (changing the fourth and fifth displays appropriately).
- p. 179: In Exercise 4.5.8,
should be
. In Exercise 4.5.7,
should be
.
- p. 180: Exercise 4.5.11 does not work as stated and should be deleted.
- p. 181: In Lemma 4.35, add “
is an integer, ” after “where”. In the proof, “incrementing
” should be “incrementing
to
“. “all dissociated subsets of
” should be “all dissociated subsets of
“.
- p. 183: In the statement of Lemma 4.37, the second “an” should be “a”.
- p. 187: In the statement of Theorem 4.41, the upper bound for
should be
rather than just
.
- p. 188: At the end of the proof of Theorem 4.41, add the following parenthetical remark: “The upper bound on
required for Corollary 2.62 is supplied by (4.37) and the lower bound on
.” In Exercise 4.6.2:
should be
(two occurrences).
- p. 189: In the discussion after Theorem 4.42, the bound
should be $latex E(A,A) >= P(A) |A|^3$.
- p. 191: In the third equation of the display, the
norms should be
(and the final term
should just be
.
- p. 193: Lemma 4.46 has a redundant “such that”.
- p. 194: In Theorem 4.47, the
should be
, and
should be
.
- p. 196: A right parenthesis is missing after the reference to Green [149]. In the penultimate line in the proof of Theorem 4.47, as well as in the sentence immediately after this proof, and in the second sentence on page 197,
should be
.
- p. 199: In the second sentence in the paragraph before the statement of Lemma 5.3, “Lemma” should be uncapitalised.
- p. 201: In the second-t0-last displayed equation,
should be
.
- p. 208: The sixth line of the long display should be
(here we use
). The seventh line should be
. The eighth line should be
. The final line remains as
(here we again use
).
- p. 211: In the statement of Lemma 5.13, “let suppose” should be just “suppose”.
- p. 226: In Exercise 5.3.4, the hypothesis “
” is missing. In exercise 5.3.2,
should be
.
- p. 236: In the proof of Proposition 5.41, all occurrences of
should be
.
- p. 239: The example in Exercise 5.5.17 is incorrect; the set
should be
in
, where
is the standard basis and one adopts the convention
; “quadrilateral” should be “pentagon” and
and
should be replaced by
throughout.
- p. 241: In the last line of the first display in the proof of Lemma 5.45,
should be
.
- p. 242: Before (5.19), a right parenthesis should be inserted after $\mathrm{Tor}(Z)$.
- p. 248: In the proof of Theorem 6.1, “probablistic” should be “probabilistic”.
- p. 249: In the second paragraph of the proof of Theorem 6.2, all occurrences of
should be
.
- p. 254: In exercise 6.2.8, the adjective “triangle-free” should be deleted. In Exercise 6.2.3, the final period should be inside the parenthesis.
- p. 260: In Exercise 6.3.5,
should be replaced with
, with the note “where
is the restricted sumset of
with itself” added.
- p. 263: In the final display, the right parenthesis after
should be deleted. Similarly for the first display on page 264.
- p. 271: In Section 6.5.2,
should be
(two occurrences).
- p. 272: The definition of
needs to be moved from page 273 to just before Lemma 6.34.
- p. 273: In Exercise 6.4.2, “Claim 6.31 and Claim 6.4” should be “equations (6.3) and (6.4)”.
- p. 279: In Proposition 7.7,
should be
.
- p. 281: In the last paragraph, “
is odd” should be “
is odd”.
- p. 285: Corollary 5.25 should be Lemma 5.25.
- p. 286: In the second paragraph, the condition
should be replaced by
, and the phrase “by Markov’s inequality” should be dropped. Similarly, in the third and fifth displays, the first occurrence of
in each should be
.
- p. 291: In the definition of
after the first display, a
is needed at the end of the integral. In the first paragraph, add “but still bounded” after “sufficiently large”.
- p. 292: In Exercise 7.3.4, the comma should be an apostrophe.
- p. 293:
should be elements of
rather than
. In Example 7.19, “which have volume” should be “which has volume”.
- p. 294: After the first proof of (7.20), “lower dimension its” should be “lower its dimension”.
- p. 299: In the first display,
should be
.
- p. ???: In Section 7.7 and in reference [101], the accent in Esseen should be dropped.
- p. 313: In Theorem 8.10, “at most
lines” should be “at most
curves”.
- p. 315: In the proof of Theorem 8.14,
should be
.
- p. 316: In the third to last line,
should be
.
- p. 331: In the third and fifth displays, the summation should run up to
rather than
. In the proof of Theorem 9.2,
should be
.
- p. 333: In the proof of Lemma 9.3, “P vanishes on contains” should be “P vanishes on a set which contains”.
- p. 346: “Cauchy’s theorem” should be “Lagrange’s theorem”.
- p. 358: In the second display of the proof of Lemma 9.43,
should be
.
- p. 363: in the last paragraph “the finite field
” should be “the ring
of formal polynomials with coefficients in the finite field
“.
- p. 370: In the last paragraph, the reference “Meshulam [248]” should instead be “Brown and Buhler [BB] (see also Frankl, Graham, and Rodl [FGR]”, where [BB] is “T. C. Brown and J. C. Buhler, Lines imply spaces in density Ramsey theory, J. Combin. Theory Ser. A 36 (1984), 214-220.”, and [FGR] is “P. Frankl, R. Graham, and V. Rodl, On subsets of abelian groups with no 3-term arithmetic progresion, J. Combin. Theory Ser. A 45 (1987), 157-161.”
- p. 371: In Exercise 10.0.3, add “The upper density of a subset
of the integers is defined as
.”.
- p. 372: In Exercise 10.0.8, add the hypothesis that no non-zero element of the groups containing
or
has order less than
.
- p. 386: In the first display,
should be
.
- p. 388: In Lemma 10.25, there should be no absolute value signs around
. In the last display,
should be
, and in the first display on page 389,
should be
.
- p. 388, 390-391: The Kronecker approximation theorem should more accurately be called a simultaneous Dirichlet approximation theorem.
- p. 391: In Lemma 10.29,
should be
, there should be an additional hypothesis of
. The bound
should be
, and the bound
should be
. In the third display of the proof, the right-hand side of 1 should be
, and in the fifth display, the right-hand side should be
.
- p. 394: in the second display,
should be
.
- p. 396: In each of the two displays after “From (10.16), we have”, there is an extra right parenthesis on the right-hand side that should be deleted.
- p. 397: In Exercise 10.4.2, Lemma 10.15 should be Lemma 10.29.
- p. 402: In (10.21),
should be
, and similarly in the folowing display.
- Page ???: In the statement of Theorem 10.31, the bound for
should be
rather than
.
- p. 405: In Exercise 10.5.1,
should be
.
- p. 412: In the second case of Corollary 10.50 the word ‘and’ should be inserted.
- p. 413: In Exercise 10.7.2,
should be
. In the second display,
should similarly be
(which is permissible since
).
- p. 414: In the first paragraph, “motivation” should be “motivations”.
- p. 430: In the last line, a right parenthesis is missing after $\exp(O(\eta^{-O(1)})$.
- p. 435: In the penultimate display,
should be
.
- p. 436: In the equation before (11.21),
should be
, and the right brace should be deleted.
- p. 437: In the definition of
,
should be
.
- p. 439. In proposition 11.12, In the last line, a right parenthesis is missing after $\exp(O(\eta_k^{-O_k(1)})$.
- P. 449: In the sixth line from the bottom, “positive upper progressions” should be “positive upper density”. In the first display in the proof of Theorem 11.23,
should be
.
- p. 450: In the last line of the proof, “non-zero
” should be “non-zero
“.
- p. 452: In Theorem 11.25,
should be
.
- p. 465: In the definition of
,
should be
; also, on the last line, “to order to” should be “in order to”.
- p. 477: In the top line, “an positive” should be “a positive”.
- p. 492: [98] and [100] refer to the same article; [98] should be deleted and redirected to [100].
Thanks to Eric Aas, Ryan Alweiss, Andrea, Louigi Addario-Berry, Khodakhast Bibak, Thomas Bloom, Lin Bo, Richard Brent, Walter Bridges, Adam Brown, Tom Brown, Andres Caicedo, Rafael Tesoro Carretero, Kestutis Cesnavicius, Mei-Chu Chang, Sheng-Fu Chiu, David Colvert, Paul Delhanty, RFZ, Mikhail Gabdullin, Moubariz Garaev, Stephen Ge, Marcel Goh, Paul Hagelstein, Le Thai Hoang, Zach Hunter, Ce Jin, Tom Koornwinder, Jarek Kuben, Nitish Kumar, Pham Lam, Choongbum Lee, Mark Lewko, Victor Lie, Chao-Ming Lin, Yang Liu, Isabel Lugo, Freddie Manners, Heiko Mattern, Vicky Neale, Danny Nguyen, Lam Pham, Gyan Prakash, Firdavs Rakhmonov, Aditya Guha Roy, Juanjo Rué, Sean, Mark Sellke, Tomer Shalev, Olof Sisask, Justin W. Smith, Sai Teja Somu, Srivastan, Thomas, Matthew Tointon, Sam van Gool, Marco Vitturi, and Mate Weirdl for corrections.

270 comments
Comments feed for this article
19 January, 2021 at 1:04 am
adityaguharoy
On page 62 line 1, equation number 2.7 the right hand side should be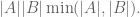 The comma inside the minimum is missing.
The comma inside the minimum is missing.
19 January, 2021 at 1:15 am
N is a number
Can you please give an idea motivating the name “additive energy” in page 61 ?
[See https://mathoverflow.net/questions/223954/where-did-the-term-additive-energy-originate -T.]
21 January, 2021 at 9:41 am
Aditya Guha Roy
Related to an already mentioned errata on page 162, there is a typo in the last line. On the last two lines of that page, I think it should say that 0 can only be represented as a sum of two squares in only one way. The squares is mentioned as elements in the book.
[Correction added, thanks – T.]
22 January, 2021 at 6:27 am
Aditya Guha Roy
Just some nitpicking : in the statement of lemma 4.20 (size bounds) on page 166, one should have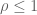 in order to ensure that
in order to ensure that  .
.
[This correction has already been noted – T.]
25 January, 2021 at 9:07 pm
adityaguharoy
On page 61 in the 5th point of the statement of Proposition 2.7 (vanishing of the Ruzsa distance), I think we should have for all non-negative integers
for all non-negative integers 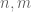 with
with 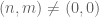 because if both
because if both 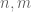 are equal to zero, then
are equal to zero, then  whence
whence  .
.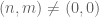 is missing in the text.
is missing in the text.
The condition
[Erratum added, thanks – T.]
25 January, 2021 at 9:13 pm
adityaguharoy
The result for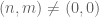 follows from
follows from ![\sigma [A] = 1](https://s0.wp.com/latex.php?latex=%5Csigma+%5BA%5D+%3D+1&bg=ffffff&fg=545454&s=0&c=20201002) by an application of the exact sum set theorem (Proposition 2.2 in the book).
by an application of the exact sum set theorem (Proposition 2.2 in the book).
27 January, 2021 at 4:24 am
adityaguharoy
On line 8 of page 63 the sum should be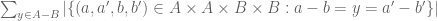 .
.
[A version of this correction is already implemented – T.]
1 February, 2021 at 9:24 pm
Aditya Guha Roy
In Corollary 2.23 shouldn’t we need the condition that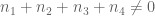 because if each
because if each  then the LHS of the display on the last line of page 73 will be
then the LHS of the display on the last line of page 73 will be 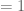 (since those sets contain the identity element
(since those sets contain the identity element  ) while the RHS will be
) while the RHS will be 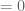 .
.
Another thing: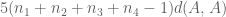 because when we apply equation 2.17 with the mentioned trivial estimates we would get
because when we apply equation 2.17 with the mentioned trivial estimates we would get ![\frac{|n_1 A - n_2 A - n_3 A +n_4 A|}{|n_1 A - n_2 A|^{1/2} |n_3 A - n_4 A|^{1/2}} \le \frac{ \delta [A] ^{5(n_1+n_2+n_3+n_4 - 1} |A| }{ | A |^{1/2} |A|^{1/2} }](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%7Cn_1+A+-+n_2+A+-+n_3+A+%2Bn_4+A%7C%7D%7B%7Cn_1+A+-+n_2+A%7C%5E%7B1%2F2%7D+%7Cn_3+A+-+n_4+A%7C%5E%7B1%2F2%7D%7D+%5Cle+%5Cfrac%7B+%5Cdelta+%5BA%5D+%5E%7B5%28n_1%2Bn_2%2Bn_3%2Bn_4+-+1%7D+%7CA%7C+%7D%7B+%7C+A+%7C%5E%7B1%2F2%7D+%7CA%7C%5E%7B1%2F2%7D+%7D&bg=ffffff&fg=545454&s=0&c=20201002) where the numerator comes from equation 2.17 and the denominator comes from the trivial estimate
where the numerator comes from equation 2.17 and the denominator comes from the trivial estimate 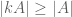 for any integer non-zero integer $k.$
for any integer non-zero integer $k.$
On the display on the last line of page 73 shouldn’t the right hand side be
But somehow I see that if the latter is also true then we need the former condition to be strengthened to because having
because having 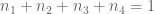 will give the same problem.
will give the same problem.
[Erratum added. The small optimisation of the $-1$ factor has been omitted from this preliminary estimate to reduce clutter. -T]
16 March, 2021 at 11:36 am
Zach Hunter
On the erratum for page 15, I am confused why you say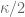 should be replaced by
should be replaced by 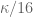 instead of 16. I have not worked out the constants for
instead of 16. I have not worked out the constants for 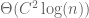 , so maybe
, so maybe 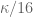 also works, but I would think that 16 is the simpler constant…
also works, but I would think that 16 is the simpler constant…
[Corrected, thanks – T.]
8 April, 2021 at 11:01 pm
Marcel Goh
Hi Prof. Tao, I am wondering if the measure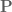 constructed at the top of page 450 is measure-preserving. It needs to be to apply Theorem 11.23, but it is not immediately obvious to me why it is. I can sort of see how one might argue that shifting the index by 1 inside the formula wouldn’t change the
constructed at the top of page 450 is measure-preserving. It needs to be to apply Theorem 11.23, but it is not immediately obvious to me why it is. I can sort of see how one might argue that shifting the index by 1 inside the formula wouldn’t change the  or
or 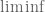 of the sequence of averages that we apply
of the sequence of averages that we apply  to. But since
to. But since  is only guaranteed to be sandwiched between the two limits, if the inner sequence is not convergent, are we always sure that
is only guaranteed to be sandwiched between the two limits, if the inner sequence is not convergent, are we always sure that  applied to the sequence is shift-invariant? Would you be able to spell this out a bit more? Thanks in advance!
applied to the sequence is shift-invariant? Would you be able to spell this out a bit more? Thanks in advance!
18 April, 2021 at 9:39 pm
Terence Tao
For any set of integers,
of integers, ![{\bf P}_{[-N_j, N_j]}(B)](https://s0.wp.com/latex.php?latex=%7B%5Cbf+P%7D_%7B%5B-N_j%2C+N_j%5D%7D%28B%29&bg=ffffff&fg=545454&s=0&c=20201002) and
and ![{\bf P}_{[-N_j, N_j]}(B+1)](https://s0.wp.com/latex.php?latex=%7B%5Cbf+P%7D_%7B%5B-N_j%2C+N_j%5D%7D%28B%2B1%29&bg=ffffff&fg=545454&s=0&c=20201002) differ by
differ by 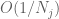 , and hence their generalised limits
, and hence their generalised limits  will agree.
will agree.
25 May, 2021 at 5:03 am
Zach Hunter
On page 51, when describing Goldbach’s conjecture, you write $2\textbf{P}$ rather than $2P$.
25 May, 2021 at 5:59 am
Aditya Guha Roy
I think is used to denote the set of all prime numbers, thus the notation.
is used to denote the set of all prime numbers, thus the notation.
25 May, 2021 at 6:14 am
Aditya Guha Roy
Please ignore my comment above, because on page 12 (line number 6 from below), it is mentioned that the set of primes will be denoted by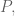 and in a previous section it is stated that
and in a previous section it is stated that  shall be used to denote the probability of an event.
shall be used to denote the probability of an event.
Apologies for any inconvenience caused due to my comment above.
25 May, 2021 at 6:05 am
N is a number
Prof. Tao, in exercise 1.1.4 on page 5 of the book you mention the term “popularity principle” for the mentioned inequality![\mathbf{E}[X \textbf{1}(X > \frac{1}{2}\mathbf{E}(X)] \geq \frac{1}{2}\mathbf{E}(X)](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BE%7D%5BX+%5Ctextbf%7B1%7D%28X+%3E+%5Cfrac%7B1%7D%7B2%7D%5Cmathbf%7BE%7D%28X%29%5D+%5Cgeq+%5Cfrac%7B1%7D%7B2%7D%5Cmathbf%7BE%7D%28X%29&bg=ffffff&fg=545454&s=0&c=20201002) . Can you suggest a reason why this nomenclature is assigned to the inequality?
. Can you suggest a reason why this nomenclature is assigned to the inequality?
[The term arose from Gowers’ use of “popular differences” in his proof of Szemeredi’s theorem, see e.g., p. 504 of https://www.cs.umd.edu/~gasarch/TOPICS/vdw/sz-thm-gowers-proof.pdf -T]
1 June, 2021 at 10:24 am
Zach Hunter
On page 26, you write $x’ \in S$ rather than $x’ + S$.
[Erratum added, thanks – T.]
23 July, 2021 at 5:38 am
Zach Hunter
On page 88, when defining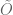 and
and 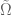 , I think that
, I think that  should be
should be  . Otherwise, the claim that
. Otherwise, the claim that  would be false, as the LHS does not depend on
would be false, as the LHS does not depend on  , however the RHS says it should get arbitrarily large as
, however the RHS says it should get arbitrarily large as  approaches 1.
approaches 1.
[Erratum added, thanks – T.]
13 September, 2021 at 9:17 pm
s1mple
In the proof of Proposition 10.24, why was it necessary to choose $p$ large enough ($2N < p N?
[If is too small, then there can be arithmetic progressions in
is too small, then there can be arithmetic progressions in ![[1,N] \hbox{ mod } p](https://s0.wp.com/latex.php?latex=%5B1%2CN%5D+%5Chbox%7B+mod+%7D+p&bg=ffffff&fg=545454&s=0&c=20201002) that do not arise from arithmetic progressions in
that do not arise from arithmetic progressions in ![[1,N]](https://s0.wp.com/latex.php?latex=%5B1%2CN%5D&bg=ffffff&fg=545454&s=0&c=20201002) (viewed as a susbet of the integers), due to wraparound effects. -T]
(viewed as a susbet of the integers), due to wraparound effects. -T]
13 September, 2021 at 9:33 pm
s1mple
In lemma 10.29, how does the last equation on page 391, follow from holder’s inequality, can you please explain? I am getting $\Omega(\sigma^{1/2}).
Even if we consider the display after ” In particular, from (4.2),(4.9)…” then if we take the maximum out on the LHS and then try to see, then also the last display comes out to be $\Omega(\sigma^{1/2}).
[Here we are using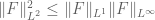 . -T]
. -T]
14 September, 2021 at 1:43 am
s1mple
Dear Tao,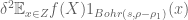 instead of
instead of 
Page 394, on the RHS (inequality) of display 2, it should be
[Corrected, thanks -T]
21 September, 2021 at 7:28 am
Aditya Guha Roy
I wanted to mention a nice expository application of the techniques in the first section of the chapter on Fourier analysis, which I learned from my friend Drago Grozev, in solving a problem from the IMO Shortlist of 1999 (the problem was the 6th combinatorics problem, better known as C6).
I am sharing the details below, because I feel that there exist some more people who will like it, just like how I did.
Let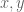 be two odd integers with
be two odd integers with 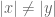 . We color the integers using 4 colors. Show that there exists two integers
. We color the integers using 4 colors. Show that there exists two integers 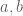 of the same color which satisfy
of the same color which satisfy 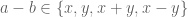 .
.
The Fourier analytic solution to this problem proceeds as follows: are positive.
are positive. where
where 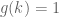 if and only if
if and only if  is colored green.
is colored green. one has
one has
 .
. must be periodic. Let
must be periodic. Let 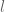 be a period of
be a period of  , and let
, and let 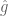 be the Fourier transform of
be the Fourier transform of  .
. deduced above it follows that
deduced above it follows that  and also
and also 
First of all notice that one can assume without losing generality that
Now let us fix one of the 4 colors, say it is green and we define a function
Now for sake of contradiction, assume that the to-be-proved claim is false.
Then for each positive integer
Next, notice that the function
Now, from the properties of
Now, using the conditions on and applying the inverse Fourier transform yields
and applying the inverse Fourier transform yields


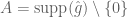
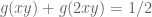 which is not possible, since
which is not possible, since  is integer-valued, a contradiction is obtained as desired.
is integer-valued, a contradiction is obtained as desired. 
and
where
thus leading to
21 September, 2021 at 8:15 am
N is a number
Prof. Tao,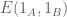 ; however the additive energy was defined for sets, and here we have their characteristic functions.
; however the additive energy was defined for sets, and here we have their characteristic functions.
on page 157 in equation 4.14 you have written
Apologies in advance if I missed taking a note of this notation defined somewhere earlier in the text.
[See the existing erratum for this equation – T.]
22 September, 2021 at 10:58 pm
N is a number
A small not-so-serious typo: on page 156 and in the 7th line after the section heading “L^p theory” I think you would like to put a colon (:) before the equality sign when you define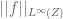 since this expression defines the quantity on the left.
since this expression defines the quantity on the left.
[Erratum added, thanks – T.]
13 November, 2021 at 5:47 pm
RFZ
Dear Prof. Tao,
on page 61 (Proposition 2.7) the fifth condition should be $|nA-mA|=|A|$ for all pairs of non-negative integers $n,m$ with $n+m\geq 1$. Because if $(n,m)=(0,0)$, then $|0A-0A|=|A|$ but $0A$ is defined to be $\{0\}$.
[This errata was already added – T.]
14 November, 2021 at 9:03 am
RFZ
Dear Prof. Tao,
on page 61 after proposition 2.7 the sentence “Later on in this chapter we shall generalize this proposition to the case when the Russia distance, difference constant, or doubling constant are little larger than 0,0, or 1, respectively…” to “Later on in this chapter we shall generalize this proposition to the case when the Russia distance, difference constant, or doubling constant are little larger than 0,1, or 1, respectively…”.
[Correction added, thanks – T.]
24 November, 2021 at 11:49 am
RFZ
Dear Prof. Tao,
I was wondering is the inequality in problem 2.2.6 on page 58 correct? I guess it should be ” at most![2\sqrt{\sigma[A]|A|}-1](https://s0.wp.com/latex.php?latex=2%5Csqrt%7B%5Csigma%5BA%5D%7CA%7C%7D-1&bg=ffffff&fg=545454&s=0&c=20201002) “. Since
“. Since  is a Sidon set, then
is a Sidon set, then ![\sigma[S]=\dfrac{|S|+1}{2}](https://s0.wp.com/latex.php?latex=%5Csigma%5BS%5D%3D%5Cdfrac%7B%7CS%7C%2B1%7D%7B2%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Also
. Also  then by problem 2.2.5 we have
then by problem 2.2.5 we have ![\sigma[S]\leq \sqrt{|A+A|}](https://s0.wp.com/latex.php?latex=%5Csigma%5BS%5D%5Cleq+%5Csqrt%7B%7CA%2BA%7C%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Combining them we obtain the following:
. Combining them we obtain the following: ![S\leq 2\sqrt{\sigma[A]|A|}-1,](https://s0.wp.com/latex.php?latex=S%5Cleq+2%5Csqrt%7B%5Csigma%5BA%5D%7CA%7C%7D-1%2C&bg=ffffff&fg=545454&s=0&c=20201002) where
where  is a Sidon set in
is a Sidon set in  . Please correct me if I’m wrong. Thanks a lot!
. Please correct me if I’m wrong. Thanks a lot!
24 November, 2021 at 12:48 pm
RFZ
Sorry I was wrong. I’ve figured out how to solve. Easy to see that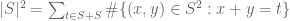 but since
but since  is a Sidon set in
is a Sidon set in  , then
, then  . Hence
. Hence  and taking square root we obtain the desired inequality.
and taking square root we obtain the desired inequality.
24 January, 2022 at 11:47 am
achraf mhamdi
I am reading this which is good but the book lacks many things. There is no complete solutions to most of the exercises and many notations introfducted in the book don’t have explanations. This is a big problem for the book. Like the function theta and omega which are not introduced in the book and just write some pages intruducting which function’s name you are talking about.
27 January, 2022 at 12:15 pm
achraf
Can you provide us with a full solution manual to the exercises, please?
14 February, 2022 at 3:11 pm
RFZ
Dear Prof. Tao! can be covered by
can be covered by  translates of
translates of 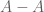 “. I think you forgot a sign
“. I think you forgot a sign 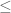 before
before 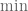 . I mean the corrected version should be the following: “In particular,
. I mean the corrected version should be the following: “In particular,  can be covered by
can be covered by  translates of
translates of 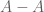 “.
“.
I have some remarks:
1) Please take a look at page 70 (Ruzsa’s covering lemma). The last line of statement of lemma says “In particular,
2) Please take a look at page 71 (Green-Ruzsa covering). The second paragraph of the proof starts as “Every time we add an element to , the size of
, the size of  …”. Corrected version should be the “the size of
…”. Corrected version should be the “the size of 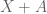 “.
“.
[Corrections added, thanks – T.]
15 February, 2022 at 6:11 pm
RFZ
Dear Prof. Tao! can be covered by
can be covered by ![\leq \delta[A]^5](https://s0.wp.com/latex.php?latex=%5Cleq+%5Cdelta%5BA%5D%5E5&bg=ffffff&fg=545454&s=0&c=20201002) translates of
translates of 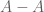 . The sign
. The sign 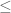 must e inserted before
must e inserted before ![\delta[A]^5](https://s0.wp.com/latex.php?latex=%5Cdelta%5BA%5D%5E5&bg=ffffff&fg=545454&s=0&c=20201002)
On page 73 the statement of Corollary 2.22 should be corrected in the following way:
[Correction added, thanks – T.]
16 February, 2022 at 8:38 am
RFZ
Dear Prof. Tao,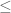 each time before
each time before ![\delta[A]](https://s0.wp.com/latex.php?latex=%5Cdelta%5BA%5D&bg=ffffff&fg=545454&s=0&c=20201002) . More precisely, it should be as follows: “This then shows that
. More precisely, it should be as follows: “This then shows that  is covered by
is covered by ![\leq \delta[A]^5](https://s0.wp.com/latex.php?latex=%5Cleq+%5Cdelta%5BA%5D%5E5&bg=ffffff&fg=545454&s=0&c=20201002) translates of
translates of  , and hence by
, and hence by ![\leq \delta[A]^{10}](https://s0.wp.com/latex.php?latex=%5Cleq+%5Cdelta%5BA%5D%5E%7B10%7D&bg=ffffff&fg=545454&s=0&c=20201002) ” translates of
” translates of 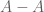 . Continuing in this fashion, an easy induction then shows
. Continuing in this fashion, an easy induction then shows  can be covered by
can be covered by ![\leq \delta[A]^{5(m+n-2)}](https://s0.wp.com/latex.php?latex=%5Cleq+%5Cdelta%5BA%5D%5E%7B5%28m%2Bn-2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) translates of
translates of 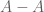 .
.
I guess you also need to add some corrections to the paragraph which follows immediately after Corollary 2.22. We need to insert the sign
16 February, 2022 at 1:33 pm
RFZ
Dear Prof. Tao,
On page 73, please take a look at Corollary 2.23. In one of the previous comments Aditya Guha Roy pointed out that this inequality is false when all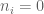 and this “correction” has been added. But I think that this inequality is true even all
and this “correction” has been added. But I think that this inequality is true even all 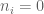 . Indeed,
. Indeed, 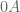 is defined to be
is defined to be 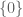 . Hence, the LHS of the inequality becomes
. Hence, the LHS of the inequality becomes 
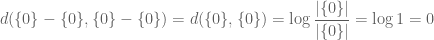 and the RHS of the inequality is also
and the RHS of the inequality is also  .
.
16 February, 2022 at 1:35 pm
RFZ
P.S. I forgot to add that please correct me if I’m wrong. Maybe I am missing some details.
[The problem lies more with the case where say but
but 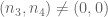 . -T]
. -T]
18 February, 2022 at 8:06 am
RFZ
Dear Prof. Tao, sorry but even if you take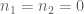 and
and 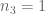 and
and  the inequality becomes
the inequality becomes 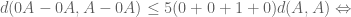
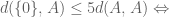
 which is true. I don’t see any issue here. Please correct me if I’m wrong!
which is true. I don’t see any issue here. Please correct me if I’m wrong!
[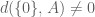 . -T]
. -T]
20 February, 2022 at 12:39 pm
RFZ
Dear Prof. Tao, holds for all
holds for all 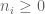 . You said that if one takes
. You said that if one takes 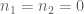 and
and  we have issues but I think it is still true. I showed it in the above comment (please take a look). Please let me know does it make sense now? Thanks a lot!
we have issues but I think it is still true. I showed it in the above comment (please take a look). Please let me know does it make sense now? Thanks a lot!
As I wrote above the inequality
16 February, 2022 at 1:57 pm
RFZ
Dear Prof. Tao,![\sigma[n_1A-n_2A]\leq \sigma[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Csigma%5Bn_1A-n_2A%5D%5Cleq+%5Csigma%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) . I think that the exponent here should be 20, not 10. Corollary 2.23 says that
. I think that the exponent here should be 20, not 10. Corollary 2.23 says that 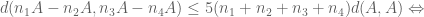
 . Taking
. Taking  and
and  , we obtain:
, we obtain: ![\frac{|n_1A-n_2A-n_2A+n_1A|}{|n_1A-n_2A|}\leq \delta[A]^{10(n_1+n_2)} \Leftrightarrow](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%7Cn_1A-n_2A-n_2A%2Bn_1A%7C%7D%7B%7Cn_1A-n_2A%7C%7D%5Cleq+++%5Cdelta%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D+%5CLeftrightarrow&bg=ffffff&fg=545454&s=0&c=20201002)
![\sigma[n_1A-n_2A]\leq \delta[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Csigma%5Bn_1A-n_2A%5D%5Cleq+%5Cdelta%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Using inequality (2.11) on the page 64 which is
. Using inequality (2.11) on the page 64 which is ![\delta[A]^{1/2}\leq \sigma[A]](https://s0.wp.com/latex.php?latex=%5Cdelta%5BA%5D%5E%7B1%2F2%7D%5Cleq+%5Csigma%5BA%5D&bg=ffffff&fg=545454&s=0&c=20201002) we obtain:
we obtain: ![\sigma[n_1A-n_2A]\leq \sigma[A]^{20(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Csigma%5Bn_1A-n_2A%5D%5Cleq+%5Csigma%5BA%5D%5E%7B20%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Please correct me if I’m wrong!
. Please correct me if I’m wrong!
Please take a look at the first inequality on the page 74:
[It’s more efficient to take and
and  , then one can avoid using (2.11). -T]
, then one can avoid using (2.11). -T]
18 February, 2022 at 7:53 am
RFZ
Dear Prof. Tao, Sorry but if you take and
and  , we obtain the following:
, we obtain the following:  and we can write as
and we can write as ![\delta[n_1A-n_2A]\leq \delta[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Cdelta%5Bn_1A-n_2A%5D%5Cleq+%5Cdelta%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) , but we need to obtain this kind of estimate for $\sigma[A]$ which is a doubling constant. Or maybe in the book it should
, but we need to obtain this kind of estimate for $\sigma[A]$ which is a doubling constant. Or maybe in the book it should ![\sigma[n_1A-n_2A]\leq \sigma[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Csigma%5Bn_1A-n_2A%5D%5Cleq+%5Csigma%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) rather than
rather than ![\delta[n_1A-n_2A]\leq \delta[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Cdelta%5Bn_1A-n_2A%5D%5Cleq+%5Cdelta%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) . Am I missing something?
. Am I missing something?
18 February, 2022 at 7:55 am
RFZ
Sorry I meant the following: Maybe it should be![\delta[n_1A-n_2A]\leq \delta[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Cdelta%5Bn_1A-n_2A%5D%5Cleq+%5Cdelta%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002) rather than
rather than ![\sigma[n_1A-n_2A]\leq \sigma[A]^{10(n_1+n_2)}](https://s0.wp.com/latex.php?latex=%5Csigma%5Bn_1A-n_2A%5D%5Cleq+%5Csigma%5BA%5D%5E%7B10%28n_1%2Bn_2%29%7D&bg=ffffff&fg=545454&s=0&c=20201002)
[Ah, I see the issue now, thanks. The simplest thing to do is to replace 10 by 20 as originally suggested – T.]
20 February, 2022 at 7:33 am
RFZ
Dear Prof. Tao, I was wondering is something wrong with my above two comments? For some reason you did not reply. Thanks a lot!
17 February, 2022 at 5:29 am
N is a number
Prof. Tao, some of the links on this page are not working for example the link to Arithmetic Ramsey theory, Math 262 notes are not working. Could you please check them?
[I think Van Vu has not maintained that web page since he moved to Yale. -T]
23 February, 2022 at 6:58 am
RFZ
Dear Prof. Tao, In exercise 2.4.5 on page 76 there is a small mistake. The bound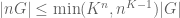 for all
for all 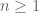 does not follow immediately from
does not follow immediately from  because
because 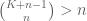 for
for 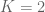 .
.
However, the above estimate could be improved slighty as follows: one can show that
 and this one immediately implies that
and this one immediately implies that 
Proof: Let’s prove that . Since
. Since  is a
is a  -approximate group, then
-approximate group, then  with
with  . By induction one can show that
. By induction one can show that  and hence
and hence 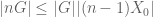 and we can estimate
and we can estimate  by inequality (2.3) on page 54. Therefore
by inequality (2.3) on page 54. Therefore 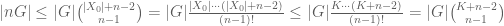 and it immediately implies that
and it immediately implies that 
[Correction added, thanks -T.]
24 February, 2022 at 11:11 am
Aditya Guha Roy
I think we can still deduce the latter claim from the former part of the exercise, by looking at the case of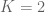 separately.
separately.
24 February, 2022 at 3:59 pm
RFZ
That could be true but I did not check it at all. Anyway the bound is better than
is better than  Moreover, it immediately implies that
Moreover, it immediately implies that 
25 February, 2022 at 8:00 am
Aditya Guha Roy
Fair enough.
27 February, 2022 at 10:23 am
RFZ
Dear Prof. Tao,
In exercise 2.4.7 on page 77 the upper bound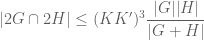 can be improved to the following one:
can be improved to the following one: 
Proof: By Ruzsa triangle inequality we have:
1) Note that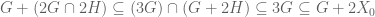 the last inequality follows from the fact that
the last inequality follows from the fact that  is a
is a  -approximate group, i.e.
-approximate group, i.e.  for some additive set
for some additive set 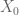 such that
such that  .
.
2) In the same way one can show that because
because  is a
is a 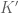 -approximate group, i.e.
-approximate group, i.e. 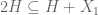 for some additive set
for some additive set 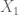 such that
such that  .
.
We see that $|G+(2G\cap 2H)|\leq |G+2X_0|\leq |G||X_0|^2\leq K^2|G|$ and
$|G+(2G\cap 2H)|\leq |G+2X_0|\leq |G||X_0|^2\leq K^2|G|$ and 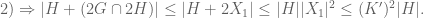
Combining these inequalities we obtain that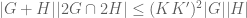 .
.
27 February, 2022 at 12:43 pm
RFZ
P.S. in this problem the final inequality which is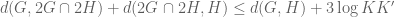 can be slightly improved as follows:
can be slightly improved as follows: 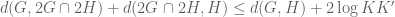 .
.
Proof: The last inequality can be be written as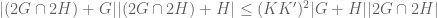 and we need to prove it. Since
and we need to prove it. Since  is a
is a  -approximate group and
-approximate group and  is a
is a 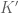 -approximate groups, then
-approximate groups, then  and
and 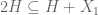 for some additive sets
for some additive sets 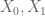 such that
such that 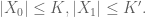
It is easy to see that and
and 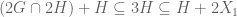 . Hence
. Hence 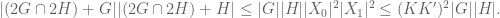 But
But  (see the first inequality of this problem) and hence
(see the first inequality of this problem) and hence 
7 March, 2022 at 4:20 pm
RFZ
Dear Prof. Tao,
What about the above 2 corrections which I’ve mentioned?
28 February, 2022 at 8:46 am
Aditya Guha Roy
On page xvii I think there is some error on line 18-19 where you say that is called dimension of
is called dimension of  and also
and also  the dimension (or rank) of
the dimension (or rank) of  (this is in context of the definition of generalized arithmetic progressions).
(this is in context of the definition of generalized arithmetic progressions).
[ are the dimensions of the progression, which is a distinct concept from the dimension of the progression, though the latter is often referred to as the rank to avoid confusion. -T]
are the dimensions of the progression, which is a distinct concept from the dimension of the progression, though the latter is often referred to as the rank to avoid confusion. -T]
7 March, 2022 at 12:33 pm
RFZ
Dear Prof. Tao,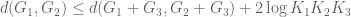 is wrong. One can take
is wrong. One can take 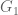 to be interval on
to be interval on  -axis of
-axis of 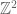 ,
, 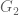 to be an interval on
to be an interval on  -axis of
-axis of 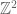 and
and 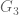 to be large rectangular box. However, the following inequality is true:
to be large rectangular box. However, the following inequality is true: 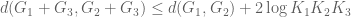 .
.
1) In problem 2.4.8 on page 77-78 the last inequality which is
2) In problem 2.4.6 one should add before
before 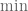 , i.e. I mean it should be
, i.e. I mean it should be  .
.
4) I see that the correction (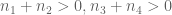 ) has been added to Corollary 2.23 on page 73-74. Even in this case if you take
) has been added to Corollary 2.23 on page 73-74. Even in this case if you take  and
and  you will obtian the following inequality
you will obtian the following inequality 
 . However, the last inequality may not be true. So therefore for safety I suggest to take all
. However, the last inequality may not be true. So therefore for safety I suggest to take all 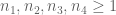 .
.
[(1) corrected, thanks. The factor in (2) can be deleted by increasing
factor in (2) can be deleted by increasing  suitably, and using Exercise 2.4.4 to handle the case of
suitably, and using Exercise 2.4.4 to handle the case of  close to 1. As for (4), I believe this estimate continues to hold in the cases indicated (for instance from the
close to 1. As for (4), I believe this estimate continues to hold in the cases indicated (for instance from the  case of (2.17) one has
case of (2.17) one has ![|3A| \leq |3A-A| \leq \delta[A]^{15} |A|](https://s0.wp.com/latex.php?latex=%7C3A%7C+%5Cleq+%7C3A-A%7C+%5Cleq+%5Cdelta%5BA%5D%5E%7B15%7D+%7CA%7C&bg=ffffff&fg=545454&s=0&c=20201002) , which implies the estimate you stated) – T.]
, which implies the estimate you stated) – T.]
12 October, 2022 at 8:16 pm
marcel goh
Dear Prof. Tao,
In the proof of irreducibility of cyclotomic polynomials (Lemma 9.48), when we constructed , we assert that it is a nontrivial monic polynomial in
, we assert that it is a nontrivial monic polynomial in ![{\bf Z}[z]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+Z%7D%5Bz%5D&bg=ffffff&fg=545454&s=0&c=20201002) , and later, we derive a contradiction because we show that, in
, and later, we derive a contradiction because we show that, in  ,
,  divides both
divides both  and
and  , when in fact these polynomials have g.c.d.
, when in fact these polynomials have g.c.d.  . However, I’m not sure how we are certain that
. However, I’m not sure how we are certain that  is not equal to
is not equal to  modulo
modulo  (the way that, say,
(the way that, say,  equals
equals  modulo
modulo  ). Thanks!
). Thanks!
21 October, 2022 at 10:54 am
Terence Tao
Sorry for the confusion. We are actually working in the formal polynomial ring![F_p[z]](https://s0.wp.com/latex.php?latex=F_p%5Bz%5D&bg=ffffff&fg=545454&s=0&c=20201002) rather than the space of polynomial functions from
rather than the space of polynomial functions from 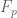 to
to 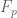 . This is still a unique factorization domain, and in this case for instance
. This is still a unique factorization domain, and in this case for instance 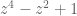 and
and  are distinct polynomials in the ring
are distinct polynomials in the ring ![F_3[z]](https://s0.wp.com/latex.php?latex=F_3%5Bz%5D&bg=ffffff&fg=545454&s=0&c=20201002) despite having the same evaluations at every point of
despite having the same evaluations at every point of 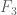 .
.
16 March, 2023 at 9:39 am
Zach Hunter
Throughout Chapter 7.7, you write “Ess\’een” several times and also do this in item [101] of the bibliography… However, it seems to me that there should be no accent! This is how the name is written on Wikipedia and the very paper you cite.
[Erratum added – T.]
31 January, 2024 at 12:24 am
Anonymous
In exercise 4.3.15, should there be an additional restriction that $M$ is self-adjoint? Without that I am only getting the result for $\text{dim}(Z) \geq 5$ instead of 3. The paper mentioned in the references seems to show this only when $M$ is self-adjoint (lemma 7.3 in https://arxiv.org/pdf/math/0503014.pdf )
[Erratum added – T.]