Starting this week, I will be teaching an introductory graduate course (Math 275A) on probability theory here at UCLA. While I find myself using probabilistic methods routinely nowadays in my research (for instance, the probabilistic concept of Shannon entropy played a crucial role in my recent paper on the Chowla and Elliott conjectures, and random multiplicative functions similarly played a central role in the paper on the Erdos discrepancy problem), this will actually be the first time I will be teaching a course on probability itself (although I did give a course on random matrix theory some years ago that presumed familiarity with graduate-level probability theory). As such, I will be relying primarily on an existing textbook, in this case Durrett’s Probability: Theory and Examples. I still need to prepare lecture notes, though, and so I thought I would continue my practice of putting my notes online, although in this particular case they will be less detailed or complete than with other courses, as they will mostly be focusing on those topics that are not already comprehensively covered in the text of Durrett. Below the fold are my first such set of notes, concerning the classical measure-theoretic foundations of probability. (I wrote on these foundations also in this previous blog post, but in that post I already assumed that the reader was familiar with measure theory and basic probability, whereas in this course not every student will have a strong background in these areas.)
Note: as this set of notes is primarily concerned with foundational issues, it will contain a large number of pedantic (and nearly trivial) formalities and philosophical points. We dwell on these technicalities in this set of notes primarily so that they are out of the way in later notes, when we work with the actual mathematics of probability, rather than on the supporting foundations of that mathematics. In particular, the excessively formal and philosophical language in this set of notes will not be replicated in later notes.
— 1. Some philosophical generalities —
By default, mathematical reasoning is understood to take place in a deterministic mathematical universe. In such a universe, any given mathematical statement (that is to say, a sentence with no free variables) is either true or false, with no intermediate truth value available. Similarly, any deterministic variable
can take on only one specific value at a time.
However, for a variety of reasons, both within pure mathematics and in the applications of mathematics to other disciplines, it is often desirable to have a rigorous mathematical framework in which one can discuss non-deterministic statements and variables – that is to say, statements which are not always true or always false, but in some intermediate state, or variables that do not take one particular value or another with definite certainty, but are again in some intermediate state. In probability theory, which is by far the most widely adopted mathematical framework to formally capture the concept of non-determinism, non-deterministic statements are referred to as events, and non-deterministic variables are referred to as random variables. In the standard foundations of probability theory, as laid out by Kolmogorov, we can then model these events and random variables by introducing a sample space (which will be given the structure of a probability space) to capture all the ambient sources of randomness; events are then modeled as measurable subsets of this sample space, and random variables are modeled as measurable functions on this sample space. (We will briefly discuss a more abstract way to set up probability theory, as well as other frameworks to capture non-determinism than classical probability theory, at the end of this set of notes; however, the rest of the course will be concerned exclusively with classical probability theory using the orthodox Kolmogorov models.)
Note carefully that sample spaces (and their attendant structures) will be used to model probabilistic concepts, rather than to actually be the concepts themselves. This distinction (a mathematical analogue of the map-territory distinction in philosophy) actually is implicit in much of modern mathematics, when we make a distinction between an abstract version of a mathematical object, and a concrete representation (or model) of that object. For instance:
- In linear algebra, we distinguish between an abstract vector space
, and a concrete system of coordinates
given by some basis of
.
- In group theory, we distinguish between an abstract group
, and a concrete representation of that group
as isomorphisms on some space
.
- In differential geometry, we distinguish between an abstract manifold
, and a concrete atlas of coordinate systems that coordinatises that manifold.
- Though it is rarely mentioned explicitly, the abstract number systems such as
are distinguished from the concrete numeral systems (e.g. the decimal or binary systems) that are used to represent them (this distinction is particularly useful to keep in mind when faced with the infamous identity
, or when switching from one numeral representation system to another).
The distinction between abstract objects and concrete models can be fairly safely discarded if one is only going to use a single model for each abstract object, particularly if that model is “canonical” in some sense. However, one needs to keep the distinction in mind if one plans to switch between different models of a single object (e.g. to perform change of basis in linear algebra, change of coordinates in differential geometry, or base change in algebraic geometry). As it turns out, in probability theory it is often desirable to change the sample space model (for instance, one could extend the sample space by adding in new sources of randomness, or one could couple together two systems of random variables by joining their sample space models together). Because of this, we will take some care in this foundational set of notes to distinguish probabilistic concepts (such as events and random variables) from their sample space models. (But we may be more willing to conflate the two in later notes, once the foundational issues are out of the way.)
From a foundational point of view, it is often logical to begin with some axiomatic description of the abstract version of a mathematical object, and discuss the concrete representations of that object later; for instance, one could start with the axioms of an abstract group, and then later consider concrete representations of such a group by permutations, invertible linear transformations, and so forth. This approach is often employed in the more algebraic areas of mathematics. However, there are at least two other ways to present these concepts which can be preferable from a pedagogical point of view. One way is to start with the concrete representations as motivating examples, and only later give the abstract object that these representations are modeling; this is how linear algebra, for instance, is often taught at the undergraduate level, by starting first with ,
, and
, and only later introducing the abstract vector spaces. Another way is to avoid the abstract objects altogether, and focus exclusively on concrete representations, but taking care to emphasise how these representations transform when one switches from one representation to another. For instance, in general relativity courses in undergraduate physics, it is not uncommon to see tensors presented purely through the concrete representation of coordinates indexed by multiple indices, with the transformation of such tensors under changes of variable carefully described; the abstract constructions of tensors and tensor spaces using operations such as tensor product and duality of vector spaces or vector bundles are often left to an advanced differential geometry class to set up properly.
The foundations of probability theory are usually presented (almost by default) using the last of the above three approaches; namely, one talks almost exclusively about sample space models for probabilistic concepts such as events and random variables, and only occasionally dwells on the need to extend or otherwise modify the sample space when one needs to introduce new sources of randomness (or to forget about some existing sources of randomness). However, much as in differential geometry one tends to work with manifolds without specifying any given atlas of coordinate charts, in probability one usually manipulates events and random variables without explicitly specifying any given sample space. For a student raised exclusively on concrete sample space foundations of probability, this can be a bit confusing, for instance it can give the misconception that any given random variable is somehow associated to its own unique sample space, with different random variables possibly living on different sample spaces, which often leads to nonsense when one then tries to combine those random variables together. Because of such confusions, we will try to take particular care in these notes to separate probabilistic concepts from their sample space models.
— 2. A simple class of models: discrete probability spaces —
The simplest models of probability theory are those generated by discrete probability spaces, which are adequate models for many applications (particularly in combinatorics and other areas of discrete mathematics), and which already capture much of the essence of probability theory while avoiding some of the finer measure-theoretic subtleties. We thus begin by considering discrete sample space models.
Definition 1 (Discrete probability theory) A discrete probability space
is an at most countable set
(whose elements
will be referred to as outcomes), together with a non-negative real number
assigned to each outcome
such that
; we refer to
as the probability of the outcome
. The set
itself, without the structure
, is often referred to as the sample space, though we will often abuse notation by using the sample space
to refer to the entire discrete probability space
.
In discrete probability theory, we choose an ambient discrete probability space
as the randomness model. We then model events
by subsets
of the sample space
. The probability
of an event
is defined to be the quantity
note that this is a real number in the interval
. An event
is surely true or is the sure event if
, and is surely false or is the empty event if
.
We model random variables
taking values in the range
by functions
from the sample space
to the range
. Random variables taking values in
will be called real random variables or random real numbers. Similarly for random variables taking values in
. We refer to real and complex random variables collectively as scalar random variables.
We consider two events
to be equal if they are modeled by the same set:
. Similarly, two random variables
taking values in a common range
are considered to be equal if they are modeled by the same function:
. In particular, if the discrete sample space
is understood from context, we will usually abuse notation by identifying an event
with its model
, and similarly identify a random variable
with its model
.
Remark 2 One can view classical (deterministic) mathematics as the special case of discrete probability theory in which
is a singleton set (there is only one outcome
), and the probability assigned to the single outcome
in
is
:
. Then there are only two events (the surely true and surely false events), and a random variable in
can be identified with a deterministic element of
. Thus we can view probability theory as a generalisation of deterministic mathematics.
As discussed in the preceding section, the distinction between a collection of events and random variable and its models becomes important if one ever wishes to modify the sample space, and in particular to extend the sample space to a larger space that can accommodate new sources of randomness (an operation which we will define formally later, but which for now can be thought of as an analogue to change of basis in linear algebra, coordinate change in differential geometry, or base change in algebraic geometry). This is best illustrated with a simple example.
Example 3 (Extending the sample space) Suppose one wishes to model the outcome
of rolling a single, unbiased six-sided die using discrete probability theory. One can do this by choosing the discrete proability space
to be the six-element set
, with each outcome
given an equal probability of
of occurring; this outcome
may be interpreted as the state in which the die roll
ended up being equal to
. The outcome
of rolling a die may then be identified with the identity function
, defined by
for
. If we let
be the event that the outcome
of rolling the die is an even number, then with this model
we have
, and
Now suppose that we wish to roll the die again to obtain a second random variable
. The sample space
is inadequate for modeling both the original die roll
and the second die roll
. To accommodate this new source of randomness, we can then move to the larger discrete probability space
, where each outcome
now having probability
; this outcome
can be interpreted as the state in which the die roll
ended up being
, and the die roll
ended up being
. The random variable
is now modeled by a new function
defined by
for
; the random variable
is similarly modeled by the function
defined by
for
. The event
that
is even is now modeled by the set
This set is distinct from the previous model
of
(for instance,
has eighteen elements, whereas
has just three), but the probability of
is unchanged:
One can of course also combine together the random variables
in various ways. For instance, the sum
of the two die rolls is a random variable taking values in
; it cannot be modeled by the sample space
, but in
it is modeled by the function
Similarly, the event
that the two die rolls are equal cannot be modeled by
, but is modeled in
by the set
and the probability
of this event is
We thus see that extending the probability space has also enlarged the space of events one can consider, as well as the random variables one can define, but that existing events and random variables continue to be interpretable in the extended model, and that probabilistic concepts such as the probability of an event remain unchanged by the extension of the model.
The set-theoretic operations on the sample space induce similar boolean operations on events:
- The conjunction
of two events
is defined through the intersection of their models:
.
- The disjunction
of two events
is defined through the the union of their models:
.
- The symmetric difference
of two events
is defined through the symmetric difference of their models:
.
- The complement
of an event
is defined through the complement of their models:
.
- We say that one event
is contained in or implies another event
, and write
, if we have containment of their models:
. We also write “
is true on
” synonymously with
.
- Two events
are disjoint if their conjunction is the empty event, or equivalently if their models
are disjoint.
Thus, for instance, the conjunction of the event that a die roll is even, and that it is less than
, is the event that the die roll is exactly
. As before, we will usually be in a situation in which the sample space
is clear from context, and in that case one can safely identify events with their models, and view the symbols
and
as being synonymous with their set-theoretic counterparts
and
(this is for instance what is done in Durrett).
With these operations, the space of all events (known as the event space) thus has the structure of a boolean algebra (defined below in Definition 4). We observe that the probability is finitely additive in the sense that
whenever are disjoint events; by induction this implies that
whenever are pairwise disjoint events. We have
and
, and more generally
for any event . We also have monotonicity: if
, then
.
Now we define operations on random variables. Whenever one has a function from one range
to another
, and a random variable
taking values in
, one can define a random variable
taking values in
by composing the relevant models:
thus maps
to
for any outcome
. Given a finite number
of random variables taking values in ranges
, we can form the joint random variable
taking values in the Cartesian product
by concatenation of the models, thus
Combining these two operations, given any function of
variables in ranges
, and random variables
taking values in
respectively, we can form a random variable
taking values in
by the formula
Thus for instance we can add, subtract, or multiply two scalar random variables to obtain another scalar random variable.
A deterministic element of a range
will (by abuse of notation) be identified with a random variable
taking values in
, whose model in
is constant:
for all
. Thus for instance
is a scalar random variable.
Given a relation on
ranges
, and random variables
, we can define the event
by setting
Thus for instance, for two real random variables , the event
is modeled as
and the event is modeled as
At this point we encounter a slight notational conflict between the dual role of the equality symbol as a logical symbol and as a binary relation: we are interpreting
both as an external equality relation between the two random variables (which is true iff the functions
,
are identical), and as an internal event (modeled by
). However, it is clear that
is true in the external sense if and only if the internal event
is surely true. As such, we shall abuse notation and continue to use the equality symbol for both the internal and external concepts of equality (and use the modifier “surely” for emphasis when referring to the external usage).
It is clear that any equational identity concerning functions or operations on deterministic variables implies the same identity (in the external, or surely true, sense) for random variables. For instance, the commutativity of addition for deterministic real numbers
immediately implies the commutativity of addition:
is surely true for real random variables
; similarly
is surely true for all scalar random variables
, etc.. We will freely apply the usual laws of algebra for scalar random variables without further comment.
Given an event , we can associate the indicator random variable
(also written as
in some texts) to be the unique real random variable such that
when
is true and
when
is false, thus
is equal to
when
and
otherwise. (The indicator random variable is sometimes called the characteristic function in analysis, and sometimes denoted
instead of
, but we avoid using the term “characteristic function” here, as it will have an unrelated but important meaning in probability theory.) We record the trivial but useful fact that Boolean operations on events correspond to arithmetic manipulations on their indicators. For instance, if
are events, we have
and the inclusion-exclusion principle
In particular, if the events are disjoint, then
Also note that if and only if the assertion
is surely true. We will use these identities and equivalences throughout the course without further comment.
Given a scalar random variable , we can attempt to define the expectation
through the model
by the formula
If the discrete sample space is finite, then this sum is always well-defined and so every scalar random variable has an expectation. If however the discrete sample space
is infinite, the expectation may not be well defined. There are however two key cases in which one has a meaningful expectation. The first is if the random variable
is unsigned, that is to say it takes values in the non-negative reals
, or more generally in the extended non-negative real line
. In that case, one can interpret the expectation
as an element of
. The other case is when the random variable
is absolutely integrable, which means that the absolute value
(which is an unsigned random variable) has finite expectation:
. In that case, the series defining
is absolutely convergent to a real or complex number (depending on whether
was a real or complex random variable.)
We have the basic link
between probability and expectation, valid for any event . We also have the obvious, but fundamentally important, property of linearity of expectation: we have
and
whenever is a scalar and
are scalar random variables, either under the assumption that
are all unsigned, or that
are absolutely integrable. Thus for instance by applying expectations to (1) we obtain the identity
We close this section by noting that discrete probabilistic models stumble when trying to model continuous random variables, which take on an uncountable number of values. Suppose for instance one wants to model a random real number drawn uniformly at random from the unit interval
, which is an uncountable set. One would then expect, for any subinterval
of
, that
will fall into this interval with probability
. Setting
(or, if one wishes instead, taking a limit such as
), we conclude in particular that for any real number
in
, that
will equal
with probability
. If one attempted to model this situation by a discrete probability model, we would find that each outcome
of the discrete sample space
has to occur with probability
(since for each
, the random variable
has only a single value
). But we are also requiring that the sum
is equal to
, a contradiction. In order to address this defect we must generalise from discrete models to more general probabilistic models, to which we now turn.
— 3. The Kolmogorov foundations of probability theory —
We now present the more general measure-theoretic foundation of Kolmogorov which subsumes the discrete theory, while also allowing one to model continuous random variables. It turns out that in order to perform sums, limits and integrals properly, the finite additivity property of probability needs to be amplified to countable additivity (but, as we shall see, uncountable additivity is too strong of a property to ask for).
We begin with the notion of a measurable space. (See also this previous blog post, which covers similar material from the perspective of a real analysis graduate class rather than a probability class.)
Definition 4 (Measurable space) Let
be a set. A Boolean algebra in
is a collection
of subsets of
which
- contains
and
;
- is closed under pairwise unions and intersections (thus if
, then
and
also lie in
); and
- is closed under complements (thus if
, then
also lies in
.
(Note that some of these assumptions are redundant and can be dropped, thanks to de Morgan’s laws.) A
-algebra in
(also known as a
-field) is a Boolean algebra
in
which is also
- closed under countable unions and countable intersections (thus if
, then
and
).
Again, thanks to de Morgan’s laws, one only needs to verify closure under just countable union (or just countable intersection) in order to verify that a Boolean algebra is a
-algebra. A measurable space is a pair
, where
is a set and
is a
-algebra in
. Elements of
are referred to as measurable sets in this measurable space.
If
are two
-algebras in
, we say that
is coarser than
(or
is finer than
) if
, thus every set that is measurable in
is also measurable in
.
Example 5 (Trivial measurable space) Given any set
, the collection
is a
-algebra; in fact it is the coarsest
-algebra one can place on
. We refer to
as the trivial measurable space on
.
Example 6 (Discrete measurable space) At the other extreme, given any set
, the power set
is a
-algebra (and is the finest
-algebra one can place on
). We refer to
as the discrete measurable space on
.
Example 7 (Atomic measurable spaces) Suppose we have a partition
of a set
into disjoint subsets
(which we will call atoms), indexed by some label set
(which may be finite, countable, or uncountable). Such a partition defines a
-algebra on
, consisting of all sets of the form
for subsets
of
(we allow
to be empty); thus a set is measurable here if and only if it can be described as a union of atoms. One can easily verify that this is indeed a
-algebra. The trivial and discrete measurable spaces in the preceding two examples are special cases of this atomic construction, corresponding to the trivial partition
(in which there is just one atom
) and the discrete partition
(in which the atoms are individual points in
).
Example 8 Let
be an uncountable set, and let
be the collection of sets in
which are either at most countable, or are cocountable (their complement is at most countable). Show that this is a
-algebra on
which is non-atomic (i.e. it is not of the form of the preceding example).
Example 9 (Generated measurable spaces) It is easy to see that if one has a non-empty family
of
-algebras on a set
, then their intersection
is also a
-algebra, even if
is uncountably infinite. Because of this, whenever one has an arbitrary collection
of subsets in
, one can define the
-algebra
generated by
to be the intersection of all the
-algebras that contain
(note that there is always at least one
-algebra participating in this intersection, namely the discrete
-algebra). Equivalently,
is the coarsest
-algebra that views every set in
as being measurable. (This is a rather indirect way to describe
, as it does not make it easy to figure out exactly what sets lie in
. There is a more direct description of this
-algebra, but it requires the use of the first uncountable ordinal; see Exercise 15 of these notes.) In Durrett, the notation
is used in place of
.
Example 10 (Borel
-algebra) Let
be a topological space; to avoid pathologies let us assume that
is locally compact Hausdorff and
-compact, though the definition below also can be made for more general spaces. For instance, one could take
or
for some finite
. We define the Borel
-algebra on
to be the
-algebra generated by the open sets of
. (Due to our topological hypotheses on
, the Borel
-algebra is also generated by the compact sets of
.) Measurable subsets in the Borel
-algebra are known as Borel sets. Thus for instance open and closed sets are Borel, and countable unions and countable intersections of Borel sets are Borel. In fact, as a rule of thumb, any subset of
or
that arises from a “non-pathological” construction (not using the axiom of choice, or from a deliberate attempt to build a non-Borel set) can be expected to be a Borel set. Nevertheless, non-Borel sets exist in abundance if one looks hard enough for them, even without the axiom of choice; see for instance Exercise 16 of this previous blog post.
The following exercise gives a useful tool (somewhat analogous to mathematical induction) to verify properties regarding measurable sets in generated -algebras, such as Borel
-algebras.
Exercise 11 Let
be a collection of subsets of a set
, and let
be a property of subsets
of
(thus
is true or false for each
). Assume the following axioms:
is true.
is true for all
.
- If
is such that
is true, then
is also true.
- If
are such that
is true for all
, then
is true.
Show that
is true for all
. (Hint: what can one say about
?)
Thus, for instance, if a property of subsets of is true for all open sets, and is closed under countable unions and complements, then it is automatically true for all Borel sets.
Example 12 (Pullback) Let
be a measurable space, and let
be any function from another set
to
. Then we can define the pullback
of the
-algebra
to be the collection of all subsets in
that are of the form
for some
. This is easily verified to be a
-algebra. We refer to the measurable space
as the pullback of the measurable space
by
. Thus for instance an atomic measurable space on
generated by a partition
is the pullback of
(viewed as a discrete measurable space) by the “colouring” map from
to
that sends each element of
to
for all
.
Remark 13 In probabilistic terms, one can interpret the space
in the above construction as a sample space, and the function
as some collection of “random variables” or “measurements” on that space, with
being all the possible outcomes of these measurements. The pullback then represents all the “information” one can extract from that given set of measurements.
Example 14 (Product space) Let
be a family of measurable spaces indexed by a (possibly infinite or uncountable) set
. We define the product
on the Cartesian product space
by defining
to be the
-algebra generated by the basic cylinder sets of the form
for
and
. For instance, given two measurable spaces
and
, the product
-algebra
is generated by the sets
and
for
. (One can also show that
is the
-algebra generated by the products
for
, but this observation does not extend to uncountable products of measurable spaces.)
Exercise 15 Show that
with the Borel
-algebra is the product of
copies of
with the Borel
-algebra.
As with almost any other notion of space in mathematics, there is a natural notion of a map (or morphism) between measurable spaces.
Definition 16 A function
between two measurable spaces
,
is said to be measurable if one has
for all
.
Thus for instance the pullback of a measurable space by a map
could alternatively be defined as the coarsest measurable space structure on
for which
is still measurable. It is clear that the composition of measurable functions is also measurable.
Exercise 17 Show that any continuous map from one topological space
to another
is necessarily measurable (when one gives
and
the Borel
-algebras).
Exercise 18 If
are measurable functions into measurable spaces
, show that the joint function
into the product space
defined by
is also measurable.
As a corollary of the above exercise, we see that if are measurable, and
is measurable, then
is also measurable. In particular, if
or
are scalar measurable functions, then so are
,
,
, etc..
Next, we turn measurable spaces into measure spaces by adding a measure.
Definition 19 (Measure spaces) Let
be a measurable space. A finitely additive measure on this space is a map
obeying the following axioms:
- (Empty set)
.
- (Finite additivity) If
are disjoint, then
.
A countably additive measure is a finitely additive measure
obeying the following additional axiom:
- (Countable additivity) If
are disjoint, then
.
A probability measure on
is a countably additive measure
obeying the following additional axiom:
- (Unit total probability)
.
A measure space is a triplet
where
is a measurable space and
is a measure on that space. If
is furthermore a probability measure, we call
a probability space.
A set of measure zero is known as a null set. A property
that holds for all
outside of a null set is said to hold almost everywhere or for almost every
.
Example 20 (Discrete probability measures) Let
be a discrete measurable space, and for each
, let
be a non-negative real number such that
. (Note that this implies that there are at most countably many
for which
– why?.) Then one can form a probability measure
on
by defining
for all
.
Example 21 (Lebesgue measure) Let
be given the Borel
-algebra. Then it turns out there is a unique measure
on
, known as Lebesgue measure (or more precisely, the restriction of Lebesgue measure to the Borel
-algebra) such that
for every closed interval
with
(this is also true if one uses open intervals or half-open intervals in place of closed intervals). More generally, there is a unique measure
on
for any natural number
, also known as Lebesgue measure, such that
for all closed boxes
, that is to say products of
closed intervals. The construction of Lebesgue measure is a little tricky; see this previous blog post for details.
We can then set up general probability theory similarly to how we set up discrete probability theory:
Definition 22 (Probability theory) In probability theory, we choose an ambient probability space
as the randomness model, and refer to the set
(without the additional structures
,
) as the sample space for that model. We then model an event
by an element
of
-algebra
, with each such element describing an event. The probability
of an event
is defined to be the quantity
An event
is surely true or is the sure event if
, and is surely false or is the empty event if
. It is almost surely true or an almost sure event if
, and almost surely false or a null event if
.
We model random variables
taking values in the range
by measurable functions
from the sample space
to the range
. We define real, complex, and scalar random variables as in the discrete case.
As in the discrete case, we consider two events
to be equal if they are modeled by the same set:
. Similarly, two random variables
taking values in a common range
are considered to be equal if they are modeled by the same function:
. Again, if the sample space
is understood from context, we will usually abuse notation by identifying an event
with its model
, and similarly identify a random variable
with its model
.
As in the discrete case, set-theoretic operations on the sample space induce similar boolean operations on events. Furthermore, since the -algebra
is closed under countable unions and countable intersections, we may similarly define the countable conjunction
or countable disjunction
of a sequence
of events; however, we do not define uncountable conjunctions or disjunctions as these may not be well-defined as events.
The axioms of a probability space then yield the Kolmogorov axioms for probability:
.
.
- If
are disjoint events, then
.
We can manipulate random variables just as in the discrete case, with the only caveat being that we have to restrict attention to measurable operations. For instance, if is a random variable taking values in a measurable space
, and
is a measurable map, then
is well defined as a random variable taking values in
. Similarly, if
is a measurable map and
are random variables taking values in
respectively, then
is a random variable taking values in
. Similarly we can create events
out of measurable relations
(giving the boolean range
the discrete
-algebra, of course). Finally, we continue to view deterministic elements of a space
as a special case of a random element of
, and associate the indicator random variable
to any event
as before.
We say that two random variables agree almost surely if the event
is almost surely true; this is an equivalence relation. In many cases we are willing to consider random variables up to almost sure equivalence. In particular, we can generalise the notion of a random variable slightly by considering random variables
whose models
are only defined almost surely, i.e. their domain is not all of
, but instead
with a set of measure zero removed. This is, technically, not a random variable as we have defined it, but it can be associated canonically with an equivalence class of random variables up to almost sure equivalence, and so we view such objects as random variables “up to almost sure equivalence”. Similarly, we declare two events
and
almost surely equivalent if their symmetric difference
is a null event, and will often consider events up to almost sure equivalence only.
We record some simple consequences of the measure-theoretic axioms:
Exercise 23 Let
be a measure space.
- (Monotonicity) If
are measurable, then
.
- (Subadditivity) If
are measurable (not necessarily disjoint), then
.
- (Continuity from below) If
are measurable, then
.
- (Continuity from above) If
are measurable and
is finite, then
. Give a counterexample to show that the claim can fail when
is infinite.
Of course, these measure-theoretic facts immediately imply their probabilistic counterparts (and the pesky hypothesis that is finite is automatic and can thus be dropped):
- (Monotonicity) If
are events, then
. (In particular,
for any event
.)
- (Subadditivity) If
are events (not necessarily disjoint), then
.
- (Continuity from below) If
are events, then
.
- (Continuity from above) If
is events, then
.
Note that if a countable sequence of events each hold almost surely, then their conjunction does as well (by applying subadditivity to the complementary events
. As a general rule of thumb, the notion of “almost surely” behaves like “surely” as long as one only performs an at most countable number of operations (which already suffices for a large portion of analysis, such as taking limits or performing infinite sums).
Exercise 24 Let
be a measurable space.
- If
is a function taking values in the extended reals
, show that
is measurable (giving
the Borel
-algebra) if and only if the sets
are measurable for all real
.
- If
are functions, show that
if and only if
for all reals
.
- If
are measurable, show that
,
,
, and
are all measurable.
Remark 25 Occasionally, there is need to consider uncountable suprema or infima, e.g.
. It is then no longer automatically the case that such an uncountable supremum or infimum of measurable functions is again measurable. However, in practice one can avoid this issue by carefully rewriting such uncountable suprema or infima in terms of countable ones. For instance, if it is known that
depends continuously on
for each
, then
, and so measurability is not an issue.
Using the above exercise, when given a sequence of random variables taking values in the extended real line
, we can define the random variables
,
,
,
which also take values in the extended real line, and which obey relations such as
for any real number .
We now say that a sequence of random variables in the extended real line converges almost surely if one has
almost surely, in which case we can define the limit (up to almost sure equivalence) as
This corresponds closely to the concept of almost everywhere convergence in measure theory, which is a slightly weaker notion than pointwise convergence which allows for bad behaviour on a set of measure zero. (See this previous blog post for more discussion on different notions of convergence of measurable functions.)
We will defer the general construction of expectation of a random variable to the next set of notes, where we review the notion of integration on a measure space. For now, we quickly review the basic construction of continuous scalar random variables.
Exercise 26 Let
be a probability measure on the real line
(with the Borel
-algebra). Define the Stieltjes measure function
associated to
by the formula
Establish the following properties of
:
- (i)
is non-decreasing.
- (ii)
and
.
- (iii)
is right-continuous, thus
for all
.
There is a somewhat difficult converse to this exercise: if is a function obeying the above three properties, then there is a unique probability measure
on
(the Lebesgue-Stieltjes measure associated to
) for which
is the Stieltjes measure function. See Section 3 of this previous post for details. As a consequence of this, we have
Corollary 27 (Construction of a single continuous random variable) Let
be a function obeying the properties (i)-(iii) of the above exercise. Then, by using a suitable probability space model, we can construct a real random variable
with the property that
for all
.
Indeed, we can take the probability space to be with the Borel
-algebra and the Lebesgue-Stieltjes measure associated to
. This corollary is not fully satisfactory, because often we may already have chosen a probability space to model some other random variables, and the probability space provided by this corollary may be completely unrelated to the one used. We can resolve these issues with product measures and other joinings, but this will be deferred to a later set of notes.
Define the cumulative distribution function of a real random variable
to be the function
Thus we see that cumulative distribution functions obey the properties (i)-(iii) above, and conversely any function with those properties is the cumulative distribution function of some real random variable. We say that two real random variables (possibly on different sample spaces) agree in distribution if they have the same cumulative distribution function. One can therefore define a real random variable, up to agreement in distribution, by specifying the cumulative distribution function. See Durrett for some standard real distributions (uniform, normal, geometric, etc.) that one can define in this fashion.
Exercise 28 Let
be a real random variable with cumulative distribution function
. For any real number
, show that
and
In particular, one has
for all
if and only if
is continuous.
Note in particular that this illustrates the distinction between almost sure and sure events: if has a continuous cumulative distribution function, and
is a real number, then
is almost surely false, but it does not have to be surely false. (Indeed, if one takes the sample space to be
and
to be the identity function, then
will not be surely false.) On the other hand, the fact that
is equal to some real number is of course surely true. The reason these statements are consistent with each other is that there are uncountably many real numbers
. (Countable additivity tells us that a countable disjunction of null events is still null, but says nothing about uncountable disjunctions.)
Exercise 29 (Skorokhod representation of scalar variables) Let
be a uniform random variable taking values in
(thus
has cumulative distribution function
), and let
be another cumulative distribution function. Show that the random variables
and
are indeed random variables (that is to say, they are measurable in any given model
), and have cumulative distribution function
. (This construction is attributed to Skorokhod, but it should not be confused with the Skorokhod representation theorem. It provides a quick way to generate a single scalar variable, but unfortunately it is difficult to modify this construction to generate multiple scalar variables, especially if they are somehow coupled to each other.)
There is a multidimensional analogue of the above theory, which is almost identical, except that the monotonicity property has to be strengthened:
Exercise 30 Let
be a probability measure on
(with the Borel
-algebra). Define the Stieltjes measure function
associated to
by the formula
Establish the following properties of
:
- (i)
is non-decreasing:
whenever
for all
.
- (ii)
and
.
- (iii)
is right-continuous, thus
for all
, where the
superscript denotes that we restrict each
to be greater than or equal to
.
- (iv) One has
whenever
are real numbers for
. (Hint: try to express the measure of a box
with respect to
in terms of the Stieltjes measure function
.)
Again, there is a difficult converse to this exercise: if is a function obeying the above four properties, then there is a unique probability measure
on
for which
is the Stieltjes measure function. See Durrett for details; one can also modify the arguments in this previous post. In particular, we have
Corollary 31 (Construction of several continuous random variables) Let
be a function obeying the properties (i)-(iv) of the above exercise. Then, by using a suitable probability space model, we can construct real random variables
with the property that
for all
.
Again, this corollary is not completely satisfactory because the probability space produced by it (which one can take to be with the Borel
-algebra and the Lebesgue-Stieltjes measure on
) may not be the probability space one wants to use; we will return to this point later.
— 4. Variants of the standard foundations (optional) —
We have focused on the orthodox foundations of probability theory in which we model events and random variables through probability spaces. In this section, we briefly discuss some alternate ways to set up the foundations, as well as alternatives to probability theory itself. (Actually, many of the basic objects and concepts in mathematics have multiple such foundations; see for instance this blog post exploring the many different ways to define the notion of a group.) We mention them here in order exclude them from discussion in subsequent notes, which will be focused almost exclusively on orthodox probability.
One approach to the foundations of probability is to view the event space as an abstract -algebra
– a collection of abstract objects with operations such as
and
(and
and
) that obey a number of axioms; see this previous post for a formal definition. The probability map
can then be viewed as an abstract probability measure on
, that is to say a map from
to
that obeys the Kolmogorov axioms. Random variables
taking values in a measurable space
can be identified with their pullback map
, which is the morphism of (abstract)
-algebras that sends a measurable set
to the event
in
; with some care one can then redefine all the operations in previous sections (e.g. applying a measurable map
to a random variable
taking values in
to obtain a random variable
taking values in
) in terms of this pullback map, allowing one to define random variables satisfactorily in this abstract setting. The probability space models discussed above can then be viewed as representations of abstract probability spaces by concrete ones. It turns out that (up to null events) any abstract probability space can be represented by a concrete one, a result known as the Loomis-Sikorski theorem; see this previous post for details.
Another, related, approach is to start not with the event space, but with the space of scalar random variables, and more specifically with the space of almost surely bounded scalar random variables
(thus, there is a deterministic scalar
such that
almost surely). It turns out that this space has the structure of a commutative tracial (abstract) von Neumann algebra. Conversely, starting from a commutative tracial von Neumann algebra one can form an abstract probability space (using the idempotent elements of the algebra as the events), and thus represent this algebra (up to null events) by a concrete probability space. This particular choice of probabilistic foundations is particularly convenient when one wishes to generalise classical probability to noncommutative probability, as this is simply a matter of dropping the axiom that the von Neumann algebra is commutative. This leads in particular to the subjects of quantum probability and free probability, which are generalisations of classical probability that are beyond the scope of this course (but see this blog post for an introduction to the latter, and this previous post for an abstract algebraic description of a probability space).
It is also possible to model continuous probability via a nonstandard version of discrete probability (or even finite probability), which removes some of the technicalities of measure theory at the cost of replacing them with the formalism of nonstandard analysis instead. This approach was pioneered by Ed Nelson, but will not be discussed further here. (See also these previous posts on the Loeb measure construction, which is a closely related way to combine the power of measure theory with the conveniences of nonstandard analysis.)
One can generalise the traditional, countably additive, form of probability by replacing countable additivity with finite additivity, but then one loses much of the ability to take limits or infinite sums, which reduces the amount of analysis one can perform in this setting. Still, finite additivity is good enough for many applications, particularly in discrete mathematics. An even broader generalisation is that of qualitative probability, in which events that are neither almost surely true or almost surely false are not assigned any specific numerical probability between or
, but are simply assigned a symbol such as
to indicate their indeterminate status; see this previous blog post for this generalisation, which can for instance be used to view the concept of a “generic point” in algebraic geometry or metric space topology in probabilistic terms.
There have been multiple attempts to move more radically beyond the paradigm of probability theory and its relatives as discussed above, in order to more accurately capture mathematically the concept of non-determinism. One family of approaches is based on replacing deterministic logic by some sort of probabilistic logic; another is based on allowing several parameters in one’s model to be unknown (as opposed to being probabilistic random variables), leading to the area of uncertainty quantification. These topics are well beyond the scope of this course.

121 comments
Comments feed for this article
14 June, 2019 at 7:59 pm
Rajeeva Karandikar
Dear Prof Tao,
This is regarding your comment about finitely additive probability theory : “One can generalise the traditional, countably additive, form of probability by replacing countable additivity with finite additivity, but then one loses much of the ability to take limits or infinite sums, which reduces the amount of analysis one can perform in this setting. Still, finite additivity is good enough for many applications, particularly in discrete mathematics.”
Well. Lots of limit theory can be done in finitely additive setting. Long ago, I had proven a meta-theorem: Almost all limit theorems that are true in countably additive setup are also true in finitely additive setup:
For the case of a sequence of independent random variables- see:
A General Principle For Limit Theorems In Finitely Additive Probability
Transactions Of The American Mathematical Society Volume 273, Number 2. October 1982
Click to access S0002-9947-1982-0667159-6.pdf
and for dependent case:
A general principle for limit theorems in finitely additive probability: The dependent case
Journal of Multivariate Analysis
Volume 24, Issue 2, February 1988, Pages 189-206
https://doi.org/10.1016/0047-259X(88)90035-8
30 August, 2019 at 8:36 am
Quentin
Dear Professor Tao,
Regarding Exercise 29, let be the sample space and suppose that there exists
be the sample space and suppose that there exists  such that
such that  . Is this possibility allowed by the definition of
. Is this possibility allowed by the definition of 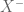 ? Isn’t
? Isn’t  undefined?
undefined?
Thanks,
Quentin
30 August, 2019 at 10:35 am
Terence Tao
This possibility can only occur with probability 0, so this is not a major issue (all the usual concepts of probability continue to hold for random variables that are only defined almost surely, as long as one only works with at most countably many such random variables at once; cf. the discussion preceding Exercise 23).
12 November, 2019 at 6:47 pm
254A, Notes 9 – second moment and entropy methods | What's new
[…] space , but this distinction will not be so important in these notes and so we shall ignore it. See this previous set of notes for more […]
30 December, 2019 at 2:06 pm
Anonymous
Dear Prof. Tao:
May I ask you if this course notes together with Durrett’s book are suitable for someone interested in learning probability theory and that also read your books on analysis?
31 December, 2019 at 6:03 pm
Terence Tao
These are notes for a first graduate course in probability; it would be expected that the students would already have been exposed to an undergraduate course in probability (similar to how students in a first course in real analysis would have been expected to already been exposed to single and multivariable calculus).
26 February, 2020 at 8:32 pm
Anonymous
The link to Durrett’s book at the top of the post is now dead, but this Wayback link works: https://web.archive.org/web/20141030190358if_/http://www.math.duke.edu:80/~rtd/PTE/PTE4_1.pdf
Can I ask if you like Rényi’s books “Foundations of Probability” and “Probability Theory”?
26 February, 2020 at 2:11 am
יומיות 03.10.2015: ספרי המדב”פ הטובים ביותר של אוקטובר, משחק ברווז וערב מפתחי משחקי מחשב בהאקרספייס, טרילוגיית קוטל המלכים, פורומים לקוסמים וע
[…] טאו, המתמטיקאי החביב על הבלוג, מעביר קורס חדש: הבסיס של תורת ההסתברות. כרגיל אצל טאו, טקסט מלא של כל ההרצאות מופיע אצלו בבלוג. […]
29 February, 2020 at 8:29 am
Anonymous
Dear Prof Tao,
In example 14, “product sigma-algebra B1xB2 is generated by E1xR2 and R1xE2”, I have difficulty understanding which set in B1 is E1 referring to since B1 contains many sets, if E1 means taking each set in B1 consecutively, wouldn’t it mean the product sigma-algebra is generated by R1xR2? Thank you.
29 February, 2020 at 9:04 am
Anonymous
Sorry, I realize the problem of my last question, and figure out what is E1, please ignore the question and thank you for the wonderful notes.
27 March, 2020 at 3:37 pm
Anonymous
In the world of mathematics, there seems to be no difference between the notion of “Bayesian probability” and that of “frequentist probability”, which are very different in the realm of statistics. Are there axioms for these two notions? Or are they really the same thing in mathematics?
6 October, 2020 at 8:45 am
adityaguharoy
Let me reply on behalf.
So, let’s address the questions one by one.
1. What is a “formal definition” of a probability ?
It comes from measure theory : a probability (or a probability measure) is a normalized finite measure.
The first definition of probability people (including myself) hear is usually the axiomatic definition named after Kolmogorov. But these two definitions (i.e., Kolmogorov’s axiomatic definition and the above mentioned measure theoretic definition) are exactly the same.
2. Do Bayesian and / or frequentists use a different definition of probability ?
NO. What they call a probability is also a normalized finite measure.
3.Do Bayesian and frequentists have different opinions on the notion of probability ?
YES. While the formal definition of probability remains the same always, the notion is slightly different. Frequentists believe in the long term behaviour to shape their probabilities. So, a frequentist would say that a fair coin has probability of showing heads = 0.5, because if you toss it many times, you’ll get roughly equal number of heads as the number of tails.
Bayesian statistics assumes a prior distribution of the parameters. So, for instance if you have a coin and you don’t know the probability that it will shows heads, then you may assume that the probability itself follows some distribution (this may be easier to understand if you consider several parallel events and the probabilities being sampled). This distribution depends on several factors (but I will not discuss about them over here).
Hope this resolves your doubt.
6 December, 2020 at 10:53 pm
Anonymous
In the definition of indicator random variable, how to derive “E is true
 ?” I cannot find the definition of “E is true”, it seems not the same as “E is surely true” in Definition 1, thanks.
?” I cannot find the definition of “E is true”, it seems not the same as “E is surely true” in Definition 1, thanks.
[This is done in the fifth bullet point after Example 3: the statement “ is true when
is true when  is true” is synonymous with “
is true” is synonymous with “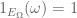 is true when $\omega \in E_\Omega$” for all models
is true when $\omega \in E_\Omega$” for all models  and all
and all  . -T]
. -T]
7 December, 2020 at 6:26 pm
Anonymous
Thank you!
23 December, 2020 at 8:05 am
Anonymous
In Definition 1, what are (definiton of) “events” and
and  ? It is clear that they are modeled by “sets”
? It is clear that they are modeled by “sets”  and
and  . Is it intentional that they are somehow agnostic in this definition?
. Is it intentional that they are somehow agnostic in this definition?
In the abstract-vs-models examples at the beginning of this text, the abstract notions of vector spaces, groups, and manifolds are all “sets” (together with some other structure): the vector space , the group
, the group  , and the manifold
, and the manifold  . Are “events” in Definition 1 sets as well?
. Are “events” in Definition 1 sets as well?
23 December, 2020 at 6:45 pm
Terence Tao
Yes, this is intentionally agnostic. Depending on one’s personal taste and the application at hand, one could think of an event in many different ways, such as
(1) A measurable subset of a sample space (identifying an event with its representative
with its representative  in some designated probability space model
in some designated probability space model  );
);
(2) An element of an abstract sigma-complete Boolean algebra (which is equipped with a countably additive probability measure);
(which is equipped with a countably additive probability measure);
(3) An idempotent in an abstract commutative tracial von Neumann algebra (this is the noncommutative probability perspective);
(4) (if one has a sufficiently informal metamathematics) actual potentially realisable events in the physical universe;
(5) etc.
Only interpretation (1) actually views an event as a set; interpretations (2), (3) view events instead as elements of various abstract spaces. The spaces themselves are sets (with additional structures), but the events need not be. (To connect with the examples at the beginning of the text, a single event would be analogous to a single vector in an abstract vector space, a single group element of an abstract group, or a single point in an abstract manifold. These objects are typically not viewed primarily as sets, though in a pure set theoretic universe they could be modeled as such.) All of the above viewpoints are useful and so I choose to remain agnostic regarding which one is to be “preferred”; any interpretation is viable so long as it can be modeled by probability spaces in the manner indicated in this blog post. In particular if one wishes to avoid philosophical and foundational issues altogether one can simply go with interpretation (1) which is the route taken in most probability texts, though if one does so one can encounter conceptual difficulties whenever one wishes to extend the probability space to add more sources of randomness, as discussed in this post. (The presentation given in this post is probably most compatible with interpretation (2); presentations in other texts may be optimised for other interpretations.)
See also the discussion in Section 4 of this post.
23 December, 2020 at 9:23 am
Anonymous
(I) On the one hand, in example 3, it is said that
… the sum of the two die rolls is a random variable taking values in
of the two die rolls is a random variable taking values in 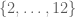 ; it cannot be modeled by the sample space
; it cannot be modeled by the sample space  , but in
, but in 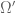 it is modeled by the function
it is modeled by the function
(II) On the other hand, it is said after example 3 that
Combining these two operations, given any function
Thus for instance we can add, subtract, or multiply two scalar random variables to obtain another scalar random variable.
As a special case where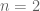 in (II), can’t we model
in (II), can’t we model  in (I) by
in (I) by 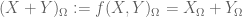 with
with 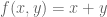 ? Why is
? Why is 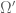 necessary in (I) but not in (II)?
necessary in (I) but not in (II)?
23 December, 2020 at 4:46 pm
Anonymous
Okay, this question seems to have been answered in this thread:
(II) assumes that has been sufficient to model
has been sufficient to model  and
and  together, while in (I)
together, while in (I)  is not sufficient.
is not sufficient.
24 December, 2020 at 6:15 pm
Ed Tam
Hi Terry,
In Exercise 18, I believe there is a small typo: it should be “R_n” instead of “R_m”.
Thanks!
[Corrected, thanks – T.]
21 March, 2022 at 5:59 am
Anonymous
In Example 3, consider the event being
being  and
and  . Then this event
. Then this event  can be only modeled in
can be only modeled in 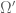 , not
, not  .
.
By counting in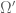 , one has
, one has  .
.
On the other hand, the probability can be “calculated/interpreted” as , where the right-hand side involves only events in the “smaller” model
, where the right-hand side involves only events in the “smaller” model  . In this particular case, one finds the probability of an event that can be only modeled in
. In this particular case, one finds the probability of an event that can be only modeled in 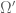 using only the information of the smaller model
using only the information of the smaller model  .
.
Is this coincidence?
21 March, 2022 at 7:42 am
Terence Tao
This occurs because we are modeling independent identically distributed variables (iid) in this example. If one is modeling variables that are independent but not identically distributed (e.g., rolling a 6-sided die and then an 8-sided die), then one can model the joint variables by the product of several different probability spaces, each of which models one of the variables, but one cannot reduce all the probability computations to that of a single random variable as in the iid case.
17 April, 2022 at 11:56 pm
Aditya Guha Roy
In Exercise 11, in
in  should be I think
should be I think 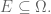
This is a beautiful result that captures the good-set principle which as far as I have seen is one of the most widely used proving techniques in measure theory, and which in my opinion is a broader form of the well-ordering principle one uses in number theory (the connection is that here we can speak about smallest sigma algebra containing a collection of subsets of and in number theory one utilizes the existence of a smallest element of every non-empty subset of the natural numbers).
and in number theory one utilizes the existence of a smallest element of every non-empty subset of the natural numbers).
21 February, 2023 at 7:37 pm
Aditya Guha Roy
Reblogged this on Aditya Guha Roy's weblog.
29 July, 2023 at 3:58 pm
Sam
Dear professor Tao:![(\mathbb R, \mathcal B[\mathbb R], \mu)](https://s0.wp.com/latex.php?latex=%28%5Cmathbb+R%2C+%5Cmathcal+B%5B%5Cmathbb+R%5D%2C+%5Cmu%29&bg=ffffff&fg=545454&s=0&c=20201002) , any function
, any function ![{F: {\mathbb R} \rightarrow [0,1]}](https://s0.wp.com/latex.php?latex=%7BF%3A+%7B%5Cmathbb+R%7D+%5Crightarrow+%5B0%2C1%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) obeying the properties (i)-(iii) can be seen as the CDF of the real random variable
obeying the properties (i)-(iii) can be seen as the CDF of the real random variable  modeled by the identity map on
modeled by the identity map on  .
.
I want to make sure that I properly understand your remark following Corollary 27. By using the probability space model
Conversely, given a real random variable , modeled say on some
, modeled say on some  , we can define the function
, we can define the function ![\mu': \mathcal B[\mathbb R]: \rightarrow [0, 1]](https://s0.wp.com/latex.php?latex=%5Cmu%27%3A+%5Cmathcal+B%5B%5Cmathbb+R%5D%3A+%5Crightarrow+%5B0%2C+1%5D&bg=ffffff&fg=545454&s=0&c=20201002) by
by  . By Example 12
. By Example 12  is a probability measure on
is a probability measure on  (with the Borel
(with the Borel  -algebra), as it’s essentially the probability measure
-algebra), as it’s essentially the probability measure  on
on  (with the pullback algebra
(with the pullback algebra ![X^*(\mathcal B[\mathbb R])](https://s0.wp.com/latex.php?latex=X%5E%2A%28%5Cmathcal+B%5B%5Cmathbb+R%5D%29&bg=ffffff&fg=545454&s=0&c=20201002) . Then
. Then  agrees in distribution to the the identity map on
agrees in distribution to the the identity map on  , using the probability model
, using the probability model ![(\mathbb R, \mathcal B[\mathbb R], \mu')](https://s0.wp.com/latex.php?latex=%28%5Cmathbb+R%2C+%5Cmathcal+B%5B%5Cmathbb+R%5D%2C+%5Cmu%27%29&bg=ffffff&fg=545454&s=0&c=20201002) .
.
Is this what you meant?
[Yes – T.]
29 July, 2023 at 4:57 pm
Sam
In the first paragraph I meant that by taking thr probability space to be with the Borel
with the Borel  -algebra and the Lebesgue-Stieltjes measure associated to
-algebra and the Lebesgue-Stieltjes measure associated to  .
.