A few months ago, I was invited to contribute an article to Scholarpedia – a Wikipedia-like experiment (using essentially the same software, in fact) in which the articles are far fewer in number, but have specialists as the primary authors (and curators) and are peer-reviewed in a manner similar to submissions to a research journal. Specifically, I was invited (with Ben Green) to author the article on Szemerédi’s theorem. The article is now submitted (awaiting review) reviewed and accepted, and can be viewed on the Scholarpedia page for that theorem. Like Wikipedia, the page is open to edits or any other comments by any user (once they register an account and login); but the edits are moderated by the curators and primary authors, who thus remain responsible for the content.
Scholarpedia seems to be an interesting experiment, trying to blend the collaborative and dynamic strengths of the wiki system with the traditional and static strengths of the peer-review system. At any rate, any feedback on my article with Ben, either at the Scholarpedia page or here, would be welcome.
[Update, July 9: the article has been reviewed, modified, and accepted in just three days – a blindingly fast speed as far as peer review goes!]
What's new 
17 comments
Comments feed for this article
9 July, 2007 at 6:00 am
John Baez
So far it seems the Scholarpedia consists of encyclopedias on three topics:
* Computational Neuroscience
* Dynamical Systems
* Computational Intelligence
Will your article become part of one of these?
(If so, I guess it must be “dynamical systems”.)
Does anyone when and how they plan to broaden out?
9 July, 2007 at 7:50 am
Terence Tao
Hi John!
I do know that they have sent out quite a lot of invitations in mathematics, and on their front page they intend their dynamical systems encyclopedia to be a “seed” for an applied maths and pure maths encyclopedia. It will be interesting to see how their project scales up…
9 July, 2007 at 11:28 am
Benjamin Thyreau
That’s nice !
Note however that Schorlarpedia differ a lot from wikipedia in another major point : Its content is _not_ under an OpenSource/Free license.
“The content on Scholarpedia is protected by international copyright, patent, and trademark laws. You may display, print or download content on Scholarpedia only for academic, non-commercial use, provided that you cite Scholarpedia. You may not publish, distribute, retransmit, sell or provide access to the content of Scholarpedia, except as permitted under applicable law and as described here.”
10 July, 2007 at 12:43 pm
Chris Hillman
Hi, Terry,
I am so glad to see you popularizing this fascinating and important subject! (Do you by any chance recall any of my posts from many years ago in which I proclaimed the bright future of “ergodic Ramsey theory”?) I guess that you know about the work of Lazlo Lovasz in extending and providing a new proof of the Szemeredi theorem, but it seems there is as yet no arXiv eprint, so perhaps not…
Picking up on John’s comment: I have been arguing for some time that the perennial (and probably unfixable) quality control problems at Wikipedia currently pose a genuine problem which urgently requires a scholarly response. I have argued that the most effective such response may lie in promoting a “grassroots” movement, founded in the universities and sponsored by the appropriate professional societies, but invoking the initiative and energy of individual faculty members who, in my vision, would— as a professional service— build and maintain narrowly focused specialist on-line encyclopedias in their own area of expertise, such as Encyclopedia of Dynamical Systems, which run under the MediaWiki engine. In my vision, each such specialized on-line encyclopedia would be managed by a small but devoted group of scholarly editors who seek to recruit expert authors of invited articles and who work to achieve balanced coverage, consistency of notation, and so on. In my vision, the principle role of “massive information resources” such as Wikipedia should be to aggregate these scholarly articles in a useful way with their own unvetted articles. The enormous success of Wikipedia amply demonstrates the irresistible popular appeal of an information resource which includes topics which would not be covered in any traditional encyclopedia, but I argue that the scholarly community needs to recognize their professional duty to fight to retain control of how the canon of mainstream knowledge and informed scholarly opinion is presented to the world. I have argued that accepting without protest the unintentional but effective transformation of the definition of “good information” from “reliable information” to “easily obtainable information” may ultimately have grave consequences for education, journalism, Big Science, public policy, the courts, electoral processes, and the scholarly enterprise itself.
Not surprisingly, my views proved controversial at Wikipedia itself, but they are based upon considerable experience, thought, and even statistical studies. Unfortunately, I have been unable to find a “safe” place to try to fully explain my reasoning, in part because it seems to be very difficult to explain why I think the essential components of civilized society which I mentioned above may in fact be under threat from Wikipedia and Web 2.0, except by discussing specific examples of the often subtle ramifications of various failure modes (manipulation/distortion of information) which I have observed at Wikipedia with distressing frequency. My concerns, unfortunately, seem to be very difficult to appreciate unless you have spent time “in the trenches”. In any case, my reasoning is too complex to adequately explain or even summarize here. I just wanted to point out that some observers experienced in the ways of wiki feel that something like Encyclopedia of Dynamical Systems may prove a far more feasible initiative than Citizendium!
I have also argued that some other promising roles for wikis include internal documentation/status boards for large websites and “research wikis” such as DispersiveWiki. So I feel that you are on the leading edge of at least two trends which I hope will catch on with your peers!
I have made some suggestions for interlinking Scholarpedia and Wikipedia at WikiProject Mathematics, where I argued this might be beneficial provided that users are provided with unobtrusive but unmistakable visual cues to assist them in maintaining “situational awareness” (see my comments there for an explanation of this term).
12 July, 2007 at 6:32 pm
Terence Tao
Dear Chris,
Certainly the topic of Szemeredi’s theorem is intimately tied in with ergodic Ramsey theory; colouring theorems such as Ramsey’s theorem or van der Waerden’s theorem seem to serve as an important model cases of density theorems such as Szemeredi’s theorem, and are often used in the proofs of such density theorems. There are some surveys by Vitaly Bergelson on this topic.
Lovasz and Szegedy have been working on the graph and hypergraph regularity and removal lemmas for a while, which in particular imply Szemeredi’s theorem as a consequence, and one can indeed extract a new proof of Szemeredi’s theorem from their methods; I would classify it as a variant of the existing hypergraph proofs of Szemeredi’s theorem due to Rodl et al. and to Gowers (I also have a couple such variants myself).
I do hope that scholarly collaborative efforts (such as Scholarpedia) mature and complement the much larger public collaborative efforts such as Wikipedia. There was certainly a vacuum of sorts due to the fact that, short of spending years at a university, even a reasonably intelligent and well-informed member of the public had very few avenues in which to get even a flavour of what is going on these days in, say, mathematics; we of course have things like popular science books, libraries, science journalism, and traditional encyclopedias, but none of these avenues is fully satisfactory. Wikipedia (and search engines such as Google) filled this vacuum largely by default; they are of course not perfect, but I definitely prefer having them to having the vacuum (or to having the vacuum filled by various forms of pseudoscience). In particular, the fact that Wikipedia does use and value credible source material, especially when it is readily available, comprehensible and convincing to a non-specialist audience, does give us a tremendous opportunity to supply such material and let the leverage of Wikipedia do the rest. In the end the solution should be better exposition, transparency, and outreach (and scholarly collaborative initiatives can certainly play an important role here); the rise of public collaborative information sources such as Wikipedia means that we can no longer rely purely on argument from authority alone to get our message across. Actually, I think that this is ultimately a very healthy development that will help prevent us from retreating too far into the ivory tower (which, in mathematics, is a particular occupational hazard).
2 August, 2007 at 7:13 pm
Xiaodong Xu
Hi, Terry,
You write
“The best-known bounds for N(k, δ) are”
I am not sure if it should be “The best known bounds for N(k, δ) are”, “best-known ” is similar to famous, yes?
3 August, 2007 at 9:36 am
Terence Tao
Dear Xiaodong,
I meant “best (known bounds)” rather than “(best known) bounds”, but I’ll reword so as to avoid the non-associative ambiguity.
9 August, 2007 at 5:50 am
Xiaodong Xu
Dear Terry,
For any a>0, there is an integer k(0), such that for any k>=k(0), if we suppose n=a^k, then there is a kAP-free subset of density 1/2 in{1,2,…,n}.
Has such a theorem proven by others? We can also have similar theorem for larger density less than 1.
This gives no new lower bound for Waerden number, but gives the limit of the method people used for the upper bound for Waerden number.
Thank you.
10 August, 2007 at 7:35 am
Terence Tao
Dear Xiaodong,
It is an interesting question. An equivalent assertion is that given any large integer n, there exists a subset A of {1,…,n} of density 1/2 such that the longest arithmetic progression contained in A only has length o(log n). Of course a random construction can easily give such a set whose longest AP has length O(log n), and doing things a bit more carefully one can get (1+o(1)) log_2 n (basically, a random construction with density 1/2+o(1) will have o(n) APs of length much larger than (1+o(1)) log_2 n, and those exceptional APs can be deleted by hand). But I don’t see how to get the o(log n); it seems stubbornly hard to refine the random construction further. One may need to look for much more algebraic examples (although the Behrend-type examples seem to be inappropriate here).
In the converse direction, the best quantitative result on Szemeredi’s theorem currently known (due to Gowers) only yields an AP of length log log log log log n or so. Presumably this can be improved.
11 August, 2007 at 11:14 pm
Xiaodong Xu
Dear Terry,
Thanks a lot!
I have considered the following question for a long time, but have no idea. Maybe SOME READERS can prove it:-)
If 2<s<t, n=W(s,t)-1, is there a red-blue coloring of {1,2,…,n} such that
1)the red subset is s AP-free;
2)the blue subset is t AP-free;
3)the number of integers in red is no more than those in blue?
Here W(s,t) is the two color Waerden number.
I think there must be such coloring, but I have no idea how to prove it.(I consider the similar problem about Ramsey graph, and have no idea too).
17 August, 2007 at 4:17 pm
Xiaodong Xu
Dear Terry,
As you told:
An equivalent assertion is that given any large integer n, there exists a subset A of {1,…,n} of density 1/2 such that the longest arithmetic progression contained in A only has length o(log n).
I have proven (c(δ)+o(1))(logn/loglogn) for δ between 0 and 1, and I will write the proof down recently:-)
Are there some known upper and lower bounds for the similar problem on Z_n?
19 August, 2007 at 6:44 am
Xiaodong Xu
Dear Terry,
The following are two part of the article Szemerédi’s theorem you wrote (with Ben Green).
1.In number theory Szemerédi’s theorem refers to the proof of the Erdős–Turán conjecture. In 1936 Erdős and Turan conjectured [1] for every value d called density 0 < d N(d,k).
2.Let k be a positive integer and let 0 < δ ≤ 1/2. A finitary version of the theorem states that there exists a positive integer
N = N(k, δ)
such that every subset of {1, 2, …, N} of size at least δN contains an arithmetic progression of length k.
In the second part, there does exist such N(k, δ), but there maybe many ones work here, yes?
For example, ifδ = 1/2, then it seems not surprising that for some M, there is a subset of {1, 2, …, 2M} of size M does not contain an arithmetic progression of length k, but every subset of {1, 2, …, 2M-1} of size M contains an arithmetic progression of length k.
(In such a case, the subset of {1, 2, …, 2M} of size M does not contain an arithmetic progression of length k, must be a subset contains both 1 and 2M).
Before we give N(k, δ) lower and upper bounds, we need decide which meaning is ours.
Let k be a positive integer and let 0 < δ ≤ 1/2.If it is a finitary of the first theorem in the first part, it should be:
there exists a positive integer
N(k, δ)
such that if N ≥ N(k, δ), then every subset of {1, 2, …, N} of size at least δN contains an arithmetic progression of length k.
I think when we consider lower bound, we are using such a DEFINITION 1 of N(k, δ).
But I am not sure if we are using this when we consider upper bound. If someone prove that
every subset of {1, 2, …, M} of size at least δM contains an arithmetic progression of length k,
should we think he has given a upper bound M for N(k, δ) ?
If we should, then what we use is not the DEFINITION 1 above, but another DEFINITION 2 as in the following theorem:
Let k be a positive integer and let 0 < δ ≤ 1/2. there exists a positive MINIMUM integer
N = N(k, δ)
such that every subset of {1, 2, …, N} of size at least δN contains an arithmetic progression of length k.
19 August, 2007 at 7:50 am
Terence Tao
Dear Xiaodong,
There are many equivalent forms of Szemeredi’s theorem, and the explicit bounds such as
which appear in different formulations tend to be comparable to each other “up to constants”. Since one cares more about the asymptotic value of these bounds than the exact value, one can thus use pretty much whatever formulation one pleases.
For instance, suppose you already know that every subset of
of density at least 
contains an arithmetic progression of length k. Then this implies the same claim when 
is replaced by a multiple 
of 
, by the pigeonhole principle (you divide 
into d intervals of length 
, and at least one of these subintervals must have density at least 
). Using this, one can relate the bounds for the two different formulations of Szemeredi’s theorem you mentioned above.
For similar reasons (to answer your earlier question), one can relate questions in {1,…,N} with questions in Z/NZ, for instance by observing that if a subset of {1,…,N/2} has no arithmetic progressions of length k when viewed as a subset of the integers, then it continues to have no arithmetic progressions of length k when the set is now interpreted as a subset of Z/NZ. In the jargon of arithmetic combinatorics, this is because {1,…,N/2} in the integers and {1,…,N/2} in Z/NZ are Freiman isomorphic of order 2.
Another useful alternative formulation of Szemeredi’s theorem comes from an argument of Varnavides (referenced in the Scholarpedia article). This shows that for N large enough, one in fact has many (comparable to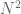
) progressions of length k in a dense subset of {1,…,N}, and not just one.
23 August, 2007 at 5:57 am
Xiaodong Xu
Given any large integer n, there exists a subset A of {1,…,n} of density 1/2 such that the longest arithmetic progression contained in A only has length (1/log2+o(1))log n/loglogn. (*)
Similar result for density δ can be proven too, where log2 should be replaced by log(1/δ).
Let r_k (n) be the maximal cardinality of a k -AP-free subset A of {1,…, n}.
Let r_k (Z_n) be the maximal cardinality of a k -AP-free subset A of Z_n.
For any odd prime p and integer n>=p, it is not difficult to prove r_p (Z_pn)>=(p-1)r_p (Z_n), and r_p (pn)>=(p-1)r_p (n),then r_p (p^t) >=r_p (Z_p^t) >= (p-1)^t.
Then I got a constrution similar to the finite version of Cantor set, based on which I proved the result (*) above.
But I found my method is not new! In the library, I found the following paper:
Small sets which meet all the k(n)-term arithmetic progressions in the interval [1, n]
Journal of Combinatorial Theory, Series A, Volume 51, Issue 2, July 1989, Pages 244-249
Tom C. Brown and Allen R. Freedman
In fact, the construction I used is the one in their paper. For any odd prime p, they proved a lower bound for N(p,δ) (they wrote g(p,ε)), so they got nearly everything I found recently! The construction is very simple, they construct it directly, instead of using r_p (p^t) >= (p-1)r_p (p^(t-1)) as I.
I guess they stop at the lower bound for N(p,δ), without giving a proof to (*), maybe for the following reason:
When they submitted their paper, the paper of Shelah on Waerden numbers had not been published yet, let alone the great work of Gowers and others’ later. At that time it is too far away and then not very interesting to give new bounds for N(p,δ) and so on. In their abstract, the main result was the answer to a problem of Erdos and etc related, but not the new bound for N(p,δ). It seems this interesting paper has been cited very few in these years.
At the end of their paper, the bounds for r_p (p^2) were given, and a result of Professor Truss was cited. The paper of Truss is
Small Sets which meet all the n-Term Arithmetic Progressions in the Interval [1, n2] ,
J. K. Truss
Bulletin of the London Mathematical Society 1991 23(2):123-127;
If p is an odd prime, and t>1, it is interesting to improve the lower and upper bounds for r_p (p^t) and r_p (Z_p^t).
14 July, 2008 at 11:16 pm
Arnab
Hi Terry,
Do you know of any notes available somewhere on Gowers’ tower-type lower bound for the Szemeredi regularity lemma? It would be great if the motivation behind the construction was explained clearly. Thanks!
18 July, 2008 at 10:30 am
Andy
Just bumping the last commenter’s request. I’d be interested too.
15 July, 2010 at 1:15 am
Xiaodong Xu
Dear Terry,
I have a problem on “off-diagonal” van der Waerden number.
The so-called“off-diagonal” van der Waerden number W(s, t), which is defined to be the least integer N such that any red/blue coloring of {1, 2, …, N} either has a red s -AP or a blue t -AP.
Maybe most people will answer yes to the following problem, but I do not know how to prove it.
Problem For any integers s<t and N<W(s, t), must there be a red/blue coloring of {1, 2, …, N} that has neither a red s -AP nor a blue t -AP, such that the red numbers in {1, 2, …, N} are no more than N/2?
I found a similar problem on Ramsey number R(s,t) earlier, and can not prove that one too.
Thanks!