This week there is a conference here at IPAM on expanders in pure and applied mathematics. I was an invited speaker, but I don’t actually work in expanders per se (though I am certainly interested in them). So I spoke instead about the recent simplified proof by Kleiner of the celebrated theorem of Gromov on groups of polynomial growth. (This proof does not directly mention expanders, but the argument nevertheless hinges on the absence of expansion in the Cayley graph of a group of polynomial growth, which is exhibited through the smoothness properties of harmonic functions on such graphs.)
— Gromov’s theorem —
Let G be an at most countable group generated by a finite set S of generators, which we can take to be symmetric (i.e. whenever
). Then we can form the Cayley graph
, whose vertices are the elements of G, and with g and gs connected by an edge for every
and
. This is a connected regular graph, with a transitive left-action of G. For any vertex x and
, one can define the ball B(x,R) in
to be the set of all vertices connected to x by a path of length at most R. We say that G has polynomial growth if we have the bound
as
; one can easily show that the left-hand side is independent of x, and that the polynomial growth property does not depend on the choice of generating set S.
Examples of finitely generated groups of polynomial growth include
- Finite groups;
- Abelian groups (e.g.
);
- Nilpotent groups (a generalisation of 2);
- Virtually nilpotent groups, i.e. it has a nilpotent subgroup of finite index (a combination of 1 and 3).
In 1981, Gromov proved that these are the only examples:
Theorem 1. (Gromov’s theorem). Let G be a finitely generated group of polynomial growth. Then G is virtually nilpotent.
Gromov’s original argument used a number of deep tools, including the Montgomery-Zippin-Yamabe structure theory of locally compact groups (related to Hilbert’s fifth problem), as well as various earlier partial results on the problem. Several proofs have subsequently been found. Recently, Kleiner obtained a proof which was significantly more elementary, although it still relies on some non-trivial partial versions of Gromov’s theorem. Specifically, it needs the following result proven by Wolf and by Milnor:
Theorem 2. (Gromov’s theorem for virtually solvable groups) Let G be a finitely generated group of polynomial growth which is virtually solvable (i.e. it has a solvable subgroup of finite index). Then it is virtually nilpotent.
The argument also needs a related result:
Theorem 3. Let G be a finitely generated amenable group which is linear, thus
for some n. Then G is virtually solvable.
This theorem is an immediate consequence of the Tits alternative, but also has a short elementary proof, due to Shalom. An easy application of the pigeonhole principle to the sequence for
shows that every group of polynomial growth is amenable. Thus Theorem 2 and Theorem 3 already give Gromov’s theorem for linear groups.
Other than Theorem 2 and Theorem 3, Kleiner’s proof of Theorem 1 is essentially self contained. The argument also extends to groups of weakly polynomial growth, which means that for some sequence of radii R going to infinity. (This extension of Gromov’s theorem was first established by van der Dries and Wilkie.) But for simplicity we only discuss the polynomial growth case here.
— Reductions —
The first few reductions follow the lines of Gromov’s original argument. The first observation is that it suffices to exhibit an infinite abelianisation of G, or more specifically to prove:
Proposition 1. (Existence of infinite abelian representation) Let G be an infinite finitely generated group of polynomial growth. Then there exists a subgroup G’ of finite index whose abelianisation
is infinite.
Indeed, if G’ has infinite abelianisation, then one can find a non-trivial homomorphism . The kernel K of this homomorphism is a normal subgroup of G’. Using the polynomial growth hypothesis, one can show that K is also finitely generated; furthermore, it is polynomial growth of one lower order (i.e. the exponent in the
bound for
is reduced by 1). An induction hypothesis then gives that K is virtually nilpotent, which easily implies that G’ (and thus G) is virtually solvable. Gromov’s theorem for infinite G then follows from Theorem 2. (The theorem is of course trivial for finite G.)
[Note: the above argument not only shows that G is virtually solvable, but moreover that G’ is the semidirect product of a virtually nilpotent group K and the integers, which acts on K by some automorphism
. So it seems to me that one does not actually need the full strength of Theorem 2 here, but only the special case of semidirect products of the above form, which might be doable “by hand”, for instance by inducting on the step of K. This might make Kleiner’s proof even more elementary, though I have not fully checked the details.]
To show Proposition 1, it suffices to show
Proposition 2. (Existence of infinite linear representation) Let G be an infinite finitely generated group of polynomial growth. Then there exists a finite-dimensional representation
whose image
is infinite.
Indeed, the image is also finitely generated with polynomial growth, and hence by Theorem 3 and Theorem 2 is virtually nilpotent (actually, for this argument we don’t need Theorem 2 and would be content with virtual solvability). If the abelianisation of
is finite, one can easily pass to a subgroup G’ of finite index and reduce the (virtual) step of
by 1, so one can quickly reduce to the case when the abelianisation is infinite, at which point Proposition 1 follows.
So all we need to do now is to prove Proposition 2.
— Harmonic functions on Cayley graphs —
Kleiner’s approach to Proposition 2 relies on the notion of a (possibly vector-valued) harmonic function on the Cayley graph . This is a function
taking values in a Hilbert space H such that
for all
. Formally, harmonic functions are local minimisers of the energy functional
where
though of course with the caveat that E(f) is often infinite. (This property is also equivalent to a certain graph Laplacian of f vanishing.)
Of course, every constant function is harmonic. But there are other harmonic functions too: for instance, on , any linear function is harmonic (regardless of the actual choice of generators). Kleiner’s proof of Proposition 2 follows by combining the following two results:
Proposition 3. Let G be an infinite finitely generated group of polynomial growth. Then there exists an (affine-) isometric (left-)action of G on a Hilbert space H with no fixed points, and a harmonic map
which is G-equivariant (thus
for all
). (Note that by equivariance and the absence of fixed points, this harmonic map is necessarily non-constant.)
Proposition 4. Let G be an finitely generated group of polynomial growth, and let
. Then the linear space of harmonic functions
which grow of order at most d (thus
on
) is finite-dimensional.
Indeed, if f is the vector-valued map given by Proposition 3, then from the G-equivariance it is easy to see that f is of polynomial growth (indeed it is Lipschitz). But the linear projections of f to scalar-valued harmonic maps lie in a finite-dimensional space, by Proposition 4. This implies that the range f(G) of f lies in a finite-dimensional space V. On the other hand, the obvious action of G on V has no fixed points (being a restriction of the action of G on H), and so the image of G in
must be infinite, and Proposition 2 follows.
It remains to prove Proposition 3 and Proposition 4. Proposition 3 follows by some more general results of Korevaar-Schoen and Mok, though Kleiner provided an elementary proof which we sketch below. Proposition 4 was initially proven by Colding and Minicozzi (for finitely presented groups, at least) using Gromov’s theorem; Kleiner’s key new observation was that Proposition 4 can be proven directly by an elementary argument based on a Poincaré inequalities.
— A non-constant equivariant harmonic function —
We now sketch the proof of Proposition 2. The first step is to just get the action on a Hilbert space with no fixed points:
Lemma 1. Let G be a countably infinite amenable group. Then there exists an action of G on a Hilbert space H with no fixed points.
This is essentially the well-known assertion that countably infinite amenable groups do not obey Property (T), but we can give an explicit proof as follows. Using amenability, one can construct a nested Følner sequence of finite sets with the property that
(say). (In the case of groups of polynomial growth, one can take
for some rapidly growing, randomly chosen sequence of radii
.) We then look at
, the Hilbert space of sequences
with
. This space has the obvious unitary action of G, defined as
. This action has a fixed point of 0, but we can delete this fixed point by considering instead the affine-isometric action
, where h is the sequence
. This sequence h does not directly lie in H, but observe that gh-h lies in H for every g. One can then easily show that this action obeys the conclusions of Lemma 1.
Another way of asserting that an action of G on H has no fixed point is to say that the energy functional defined by
is always strictly positive. So Lemma 1 concludes that there exists an action of G on a Hilbert space on which E is strictly positive. It is possible to then conclude that there exists another action of G on another Hilbert space on which the energy E is not only strictly positive, but actually attains its minimum at some vector v. This observation follows from more general results of Fisher and Margulis, but one can also argue directly as follows. For every
and
, there must exist a vector v which almost minimises E in the sense that
whenever
, since otherwise one could iterate and sum a Neumann-type series to obtain a fixed point of v. But then by shifting v to the origin, and taking an ultrafilter limit (!) as
and
, we obtain the claim.
Some elementary calculus of variations then shows that if v is the energy minimiser, the map is a harmonic G-equivariant function from G to H, and Proposition 2 follows.
— Poincaré’s inequality, and the complexity of harmonic functions —
Now we turn to the proof of Proposition 4, which is the main new ingredient in Kleiner’s argument. To simplify the exposition, let us cheat and suppose that the polynomial growth condition is replaced by the slightly stronger doubling condition
. (In practice, one can use pigeonholing arguments to show that polynomial growth implies doubling on large ranges of scales, which turns out to suffice.) Similarly, to simplify the argument, let us pretend that the harmonic functions
are not only of polynomial growth, but also obey a doubling condition
.
The key point is to exploit the fact that harmonic functions are fairly smooth. For instance, a simple “integration by parts” argument shows that if u is harmonic, then
(1);
this estimate can be established by the usual trick of replacing the summation over with a smoother cutoff function and then expanding out the gradient square.
To use this gradient control, Kleiner established the Poincaré inequality
(2)
assuming the doubling condition on balls. This inequality (a variant of a similar inequality of Coulhon and Saloff-Coste) is actually quite easy to prove. Observe that if , then x=yg for some
. Thus it suffices to show that
for each such g. But by expanding g as a product of at most 2R generators, splitting as a telescoping series, and using Cauchy-Schwarz, the result follows easily.
Combining (1) and (2), one sees that a harmonic function which is controlled on a large ball , becomes nearly constant on small balls
(morally speaking, we have
“on the average” on such small balls). In particular, given any
, one can now obtain an inequality of the form
where ranges over a cover of
by balls
of radius
(the number of such balls can be chosen to be polynomially bounded in
, by the doubling condition). As a consequence, we see that if a harmonic function
obeys a doubling condition, and has zero average on each ball
, then it vanishes identically. Morally speaking, this shows that the space of functions that obeys the doubling condition has finite dimension (bounded by the number of such balls), yielding Proposition 4 in the doubling case. It requires a small amount of combinatorial trickery to obtain this conclusion in the case when u and the balls
exhibit polynomial growth rather than doubling, but the general idea is still the same.
[Update, Feb 17: some discrepancies in the order of group multiplication (e.g. left actions vs. right actions) fixed (I think…).]

16 comments
Comments feed for this article
17 February, 2008 at 9:52 am
IU student
Hi Dr. Tao,
Since you posted this article, I am courious that do you know any interesting theorems about ergodic theorems on nilpotent Lie groups or Lie groups of polynomial growth. My question might be too abstract.:)
17 February, 2008 at 10:59 am
Terence Tao
Dear IU student,
For amenable groups (which include nilpotent groups and groups of polynomial growth as special cases), most of the standard ergodic theorems continue to apply with only minor modifications (at least if one is willing to restrict one’s average to lie along a Folner sequence). This observation is already implicitly in the classical work of Wiener; some further refinements in this direction can be found in a 1987 Journal d’Analyse paper of Ornstein-Weiss, and a 2001 Inventiones paper of Lindenstrauss.
There are some ergodic theorems for non-amenable groups too, though the theory here is significantly less systematic. For instance there is a 1997 Annals paper of Nevo and Stein which considers semisimple groups (and an earlier 1994 Acta paper by the same authors considering free groups).
20 February, 2008 at 10:20 am
Terence Tao
I am communicating here an observation from my colleague, Yehuda Shalom, who noted that one does not need the full strength of Proposition 3 (constructing the vector-valued equivariant harmonic map) in order to deduce Proposition 2 from Proposition 4. Instead, all one needs is a single non-constant scalar harmonic map f of polynomial growth. Indeed, observe that G acts by left rotation on the space V of harmonic maps of a fixed polynomial growth, which is finite dimensional by Proposition 4. If the image of f is infinite then Proposition 2 is immediate, so suppose the image of f is finite. Then there is a normal subgroup N of G of finite index which stabilises f (and everyone else in the image of f also). Because of this, the harmonic map f on G pushes down to a harmonic map on the quotient space N\G (which still has a right-action of the generator set S). But it is easy to see that a harmonic map on a finite connected graph is constant, and so f is constant, a contradiction.
29 February, 2008 at 6:00 pm
David Fisher
Hi Terry,
While this isn’t directly germane to your post, it
is little known and should be better known. I
only learned it myself a few months ago. Figure if I say it here, more people will know it.
There is a relatively short account of the main
results of the Montgomery-Zippin-Yamabe theory of locally compact groups. It is in a twenty page paper by Joram Hirschfeld see http://www.ams.org/mathscinet-getitem?mr=967314.
The proof is written in the language of nonstandard
analysis, but I think it should also be possible to give a standard version that would also be substantially simpler than the usual references to
books of Montgomery-Zippin or Kaplansky.
The fact that Kleiner’s proof doesn’t use this stuff at all is still a major breakthrough.
Best,
David
2 March, 2008 at 10:09 am
Terence Tao
Dear David,
Thanks for the reference! It indeed is a surprise that this sort of thing is not better known (for instance, MathSciNet lists no citations for this paper).
22 April, 2008 at 2:45 am
jrluw
By the way, your intuition that it should be easier to prove Theorem 2 in the case of semidirect products K x Z (where K is virtually nilpotent) seems correct. It is done in an appendix to Gromov’s original paper (by Tits): http://www.numdam.org/item?id=PMIHES_1981__53__53_0.
15 June, 2008 at 8:21 am
Eigenvalue multiplicity and growth of groups « tcs math - some mathematics of theoretical computer science
[…] and the structure of finite groups. Earlier this year at an IPAM conference on expander graphs, Terry Tao presented Bruce Kleiner’s new proof of Gromov’s theorem. After the talk, Luca Trevisan asked whether there exists an analog of certain steps in the proof […]
5 October, 2008 at 5:27 am
student
Dear Terry,
Sorry for this probably very stupid question,
but how do you define the gradient of f if it is a function from a graph (the Cayley graph) to the reals?
5 October, 2008 at 8:53 am
Terence Tao
Dear student,
I define the gradient (or more precisely, the magnitude squared
(or more precisely, the magnitude squared  ) in the second display after Proposition 2. One could take the gradient to be the |S|-dimensional (H-valued) vector with components
) in the second display after Proposition 2. One could take the gradient to be the |S|-dimensional (H-valued) vector with components 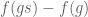 for
for 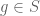 , after normalising the norm of this vector space by
, after normalising the norm of this vector space by  .
.
4 March, 2009 at 4:09 pm
Steven Heilman
Concerning the existence of Harnack Inequalities in this setting (i.e. groups of polynomial growth): they do actually exist. The modern procedure of proof is fairly abstract, as in say, the proof of Birkhoff’s Ergodic Theorem via the Maximal Lemma. Moderate technicalities aside, the result basically holds in any setting with a specific Poincare inequality and volume doubling. For the theorem, see:
Theorem VIII.3.6 of “Analysis and Geometry on Groups”, by Varopolous et al.
Also, a good survey of these kinds of results is:
“Sobolev Inequalities in Familiar and Unfamiliar Settings” by L. Saloff-Coste, in “Sobolev Spaces in Mathematics I” by V. Maz’ya, 2008.
29 March, 2009 at 4:13 am
Mikhail Gromov wins 2009 Abel prize « What’s new
[…] The prize is, of course, richly deserved. I have mentioned some of Gromov’s work here on this blog; for instance, the Bishop-Gromov inequality in Riemannian geometry (which (together with its parabolic variant, the monotonicity of Perelman reduced volume) plays an important role in Perelman’s proof of the Poincaré conjecture), the concept of Gromov-Hausdorff convergence (a version of which is also key in the proof of the Poincaré conjecture), and Gromov’s celebrated theorem on groups of polynomial growth, which I discussed in this post. […]
23 October, 2009 at 12:56 pm
A finitary version of Gromov’s polynomial growth theorem « What’s new
[…] hypothesis to requiring (1) just for infinitely many scales ; the later proof by Kleiner (which I blogged about here) also has this relaxed […]
18 February, 2010 at 3:31 pm
A proof of Gromov’s theorem « What’s new
[…] The original proof of Gromov’s theorem was quite non-elementary, using an infinitary limit and exploiting the work surrounding the solution to Hilbert’s fifth problem. More recently, Kleiner provided a proof which was more elementary (based in large part on an earlier paper of Colding and Minicozzi), though still not entirely so, relying in part on (a weak form of the) Tits alternative and also on an ultrafilter argument of Korevaar-Schoen and Mok. I discuss Kleiner’s argument more in this previous blog post. […]
23 January, 2011 at 7:13 am
The Peter-Weyl theorem, and non-abelian Fourier analysis on compact groups « What’s new
[…] role in Gromov’s proof of his theorem on groups of polynomial growth (discussed previously on this blog), and in a more recent paper of Hrushovski on approximate groups (also discussed […]
23 June, 2011 at 11:42 pm
Planar rooted trees and Baker-Campbell-Hausdorff formula | chorasimilarity
[…] paper may be relevant (check also the bibliography!) for the subject of writing “finitary“, “noncommutative” BCH formulae, from self-similarity arguments using […]
27 August, 2011 at 11:35 am
254A, Notes 0 – Hilbert’s fifth problem and related topics « What’s new
[…] and Minicozzi on harmonic functions of polynomial growth. (This latter proof is discussed in these previous blog posts.) The proof we will give in these notes is more recent, based on an . We remark […]