Even fairly good students, when they have obtained the solution of the problem and written down neatly the argument, shut their books and look for something else. Doing so, they miss an important and instructive phase of the work. … A good teacher should understand and impress on his students the view that no problem whatever is completely exhausted.
One of the first and foremost duties of the teacher is not to give his students the impression that mathematical problems have little connection with each other, and no connection at all with anything else. We have a natural opportunity to investigate the connections of a problem when looking back at its solution. (George Pólya, “How to Solve It“)
Learning never really stops in this business, even in your chosen specialty; for instance I am still learning surprising things about basic harmonic analysis, more than ten years after writing my thesis in the topic.
Just because you know a statement and proof of Fundamental Lemma X, you shouldn’t take that lemma for granted; instead, you should dig deeper until you really understand what the lemma is all about:
- Can you find alternate proofs?
- If you know two proofs of the lemma, do you know to what extent the proofs are equivalent? Do they generalise in different ways? What themes do the proofs have in common? What are the other relative strengths and weaknesses of the two proofs?
- Do you know why each of the hypotheses are necessary?
- What kind of generalizations are known/conjectured/heuristic?
- Are there weaker and simpler versions which can suffice for some applications?
- What are some model examples demonstrating that lemma in action?
- When is it a good idea to use the lemma, and when isn’t it?
- What kind of problems can it solve, and what kind of problems are beyond its ability to assist with?
- Are there analogues of that lemma in other areas of mathematics?
- Does the lemma fit into a wider paradigm or program?
It is particularly useful to lecture on your field, or write lecture notes or other expository material, even if it is just for your own personal use. You will eventually be able to internalise even very difficult results using efficient mental shorthand; this not only allows you to use these results effortlessly, and improve your own ability in the field, but also frees up mental space to learn even more material.
Another useful way to learn more about one’s field is to take a key paper in that field, and perform a citation search on that paper (i.e. search for other papers that cite the key paper). There are many tools for citation searches nowadays; for instance, MathSciNet offers this functionality, and even a general-purpose web search engine can often give useful “hits” that one might not have previously been aware of.
See also “ask yourself dumb questions“.

63 comments
Comments feed for this article
2 August, 2020 at 8:38 pm
Imran Hussain
Thanks professor for making these wonderful advices available on your blog .Hope you will continue to write such advices.
11 August, 2020 at 12:11 am
Hani fathima
Hello Professor,
I am newly PhD scholar who is interested to learn and relearn Mathematics.It would be a great help if you provide some tips on how should i work on my Thesis.What are the books should i read before i start my PhD?
Thank You
25 September, 2020 at 7:07 am
잘 보일수록 자세히 보자. – My Fortress
[…] 방법을 통해 정리를 이해할 수 있을까? 테렌스 타오는 글 ‘Learn and relearn your field‘에서 다음 질문들을 생각해보길 […]
25 September, 2020 at 9:50 am
Anonymous
Don’t know English?
26 August, 2021 at 11:51 am
Work Hard by somerandomness - HackTech.news
[…] and then ultimately writing up a complete and detailed treatment of the topic. (See also “learn and relearn your field“.) It would be very pleasant if one could just dream up the grand ideas and let some […]
22 June, 2022 at 6:19 am
roquaiya perween
The world’s greatest mathematician is still learning things about basic harmonic analysis. Wow. 😨😱😱
22 June, 2022 at 11:36 am
Anonymous
Modesty is generally considered as a good qualification.
22 June, 2022 at 12:00 pm
Anonymous
Talk as if all fundamental harmonic analysis questions are solved.
25 June, 2022 at 12:26 am
Aditya Guha Roy
This is nice. Recently I came across a complex analysis problem in an exam which I was not able to solve during the exam (thanks to my high nervousness which ruined it all), but later on I realized the solution and in fact realized another simple solution which basically boils down the problem to a real analysis question and offers better insight.
The problem was this: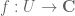 is holomorphic where
is holomorphic where  is an open subset of the complex numbers. Let
is an open subset of the complex numbers. Let 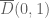 (the closed unit ball centered at
(the closed unit ball centered at  ) lie completely inside
) lie completely inside 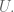 If
If  is real-valued on the boundary of this ball, then show that
is real-valued on the boundary of this ball, then show that  is constant inside the disk.
is constant inside the disk.
suppose
One way to do this is: to conclude that
to conclude that  is real valued inside the disk and then use the open mapping theorem.
is real valued inside the disk and then use the open mapping theorem.
apply maximum principle to the imaginary part of
(Sigh that I figured it out only epsilon moments after the exam ended.)
A more elementary way to do this is: is real valued inside the disk, then use the uniqueness of harmonic conjugates to obtain the claim.
is real valued inside the disk, then use the uniqueness of harmonic conjugates to obtain the claim.
apply maximum principle to conclude that
(This avoids the open mapping theorem.)
I was in general too obsessed with this problem, and tried to re-solve it by caputing the essence, and that led me to this new solution.
26 June, 2022 at 8:45 am
Anonymous
Another simple proof is to use the fact that the imaginary part of is hamonic on U and vanishes on the unit circle, so (by the maximum and minimum principle) it is bounded (both above and below) in the open unit disk by 0 – i.e it vanishes identically on the open unit disk, so in particular its first partial derivatives with respect to
is hamonic on U and vanishes on the unit circle, so (by the maximum and minimum principle) it is bounded (both above and below) in the open unit disk by 0 – i.e it vanishes identically on the open unit disk, so in particular its first partial derivatives with respect to 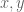 (the real and imaginary coordinates) also vanishes identically inside the disk, hence (by the Cauchy-Riemann equations) also the first partial derivatives of the real part of
(the real and imaginary coordinates) also vanishes identically inside the disk, hence (by the Cauchy-Riemann equations) also the first partial derivatives of the real part of  are vanishing identically inside the disk – which implies that f is constant inside the disk.
are vanishing identically inside the disk – which implies that f is constant inside the disk.