Van Vu and I have just uploaded to the arXiv our preprint “On the permanent of random Bernoulli matrices“, submitted to Adv. Math. This paper establishes analogues of some recent results on the determinant of random Bernoulli matrices (matrices in which all entries are either +1 or -1, with equal probability of each), in which the determinant is replaced by the permanent.
More precisely, let M be a random Bernoulli matrix, with n large. Since every row of this matrix has magnitude
, it is easy to see (by interpreting the determinant as the signed volume of a parallelopiped) that
is at most
, with equality being satisfied exactly when M is a Hadamard matrix. In fact, it is known that the determinant
has magnitude
with probability
; for a more precise result, see my earlier paper with Van. (There is in fact believed to be a central limit theorem for
; see this paper of Girko for details.) These results are based upon the elementary “base times height” formula for the volume of a parallelopiped; the main difficulty is to understand what the distance is from one row of M to a subspace spanned by several other rows of M.
The permanent looks formally very similar to the determinant, but does not have a geometric interpretation as a signed volume of a parallelopiped and so can only be analysed combinatorially; the main difficulty is to understand the cancellation that can arise from the various signs in the matrix. It can be somewhat larger than the determinant; for instance, the maximum value of
for a Bernoulli matrix M is
, attaned when M consists entirely of +1’s. Nevertheless, it is not hard to see that
has the same mean and standard deviation as
, namely 0 and
respectively, which shows that
is at most
with probability 1-o(1). Our main result is to show that one also has that
is at least
with probability 1-o(1), thus obtaining the analogue of the previously mentioned result for the determinant (though our o(1) bounds are significantly weaker).
In particular, this shows that the probability that the permanent vanishes completely is o(1) (in fact, we get a bound of for some absolute constant
). This result appears to be new (although there is a cute observation of Alon (see e.g. this paper of Wanless for a proof) that if
is one less than a power of 2, then every Bernoulli matrix has non-zero permanent). In contrast, the probability that the determinant vanishes completely is conjectured to equal
(which is easily seen to be a lower bound), but the best known upper bound for this probability is
, due to Bourgain, Vu, and Wood.
Roughly speaking, the strategy is to view the permanent of a Bernoulli matrix recursively as a random signed combination of the permanent of its
minors formed from its first n-1 rows, which one can view as the “parents” of the original matrix. The idea is then to take a sort of “genetic” or “evolutionary” viewpoint, and ask how likely the trait of having a large permanent is of being passed from parents to children. The key point is that this trait is “dominant” rather than “recessive”: as long as just one of the parents has a large permanent, it is likely that the child will have large permanent as well (and if many of the parents have large permanent, the child is likely to have an even larger permanent). Our main tool for doing this is a classical inequality of Littlewood-Offord type, due to Erdős.
However, there is still a non-negligible chance that there is enough cancellation that a child, even one with many parents with large permanent, may end up having unexpectedly small or vanishing permanent. To avoid these failure probabilities adding up to overwhelm the analysis, we have to exploit some independence. For instance, if , a
minor with large permanent will have
minors as children. Each child has at least a 1/2 chance of having a permanent as large as that of its parent (if a certain entry of the
row has a favourable sign). These events are sufficiently independent (in a certain martingale sense) that the probability that none of these children have large permanent is exponentially small – at most
. (The main technical tool we use to prove bounds such as this is Azuma’s inequality.)
Just by using the above observations (and crude probabilistic tools such as the union bound and the first moment method), it is already fairly straightforward to show that there exist many minors with large permanent (of size about
) as long as
for some
. The trickiest part is to manage the last few generations of the evolution, in which we need to get a large number of
minors with large permanent (this will imply that the full
matrix has large permanent with high probability, thanks to Erdős’ Littlewood-Offord inequality). The main difficulty is that there is a loss of independence which prevents one from obtaining the exponentially small failure probabilities one enjoyed in previous generations. The main idea to overcome this is to locate several “disjoint lineages” of
minors with large permanent, so that each of which has a fairly independent probability of eventually generating a
minor with large permanent. Again, Azuma’s inequality and Erdős’ Littlewood-Offord inequality are our main tools here.
Because we were trying to optimise the strength of our result (both in getting the lower bound for the magnitude of the permanent, and getting a reasonable bound on the failure probability), the actual arguments get slightly technical at times. I have uploaded here a very early draft of our paper, in which we prove the weaker result that with probability 1-o(1); the argument here is only a few pages long but already captures many of the key ideas. (This draft was mostly written by myself; Van then improved the bounds and results significantly, leading to the version that is on the arXiv.)

8 comments
Comments feed for this article
16 April, 2008 at 2:24 pm
nobody
Dear Professor Tao,
Another fantastic post – the genetic ideas are beautifully imaginative! Are such inheritance methods common in probabalistic combinatorics?
As for a geometric interpretation of the permanent, we can think of the determinant of a vector space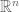 (which is just a vector bundle over a point) as a section of the top (n-th) exterior power of that vector bundle; equally we can regard the permanent as a section of the n-th symmetric tensor bundle – and given a Young diagram, we can play the same sort of game for any immanant (the notion of which was completely new to me!). Of course, whether this is actually more ‘geometrical’ is a matter of debate but at least it uses the right words :-)
(which is just a vector bundle over a point) as a section of the top (n-th) exterior power of that vector bundle; equally we can regard the permanent as a section of the n-th symmetric tensor bundle – and given a Young diagram, we can play the same sort of game for any immanant (the notion of which was completely new to me!). Of course, whether this is actually more ‘geometrical’ is a matter of debate but at least it uses the right words :-)
BTW there is a slight omission in your post – you need to specify a distribution for the 1s and -1s above – in your paper they are i.i.d. with equal probability. Have you investigated other distributions – in particular, allowing more values than 1 and -1?
16 April, 2008 at 2:33 pm
Terence Tao
Dear nobody,
Thanks for the comments. Our arguments extend to fairly general distributions as long as all the entries are independent, but we did not seek the most general formulation for which our arguments work. There is some literature (cited in the paper) for the case when all entries are non-negative, in which the situation is much better understood (there is substantially less cancellation). For instance, the case of permanents of random 0/1 matrices is more or less equivalent to counting Hamiltonian cycles in a random directed graph, which has been well studied. Once the coefficients are bounded away from zero, there are even some central limit theorems known for the permanent.
You are right that the permanent does have some sort of geometric interpretation in terms of the top symmetric power, though I am not sure how to exploit it (there is no analogue of the base times height formula in that setting, for instance). Our methods rely purely on cofactor expansions instead, though there may be other properties of the permanent (e.g. symmetry and multilinearity) which could eventually be useful.
16 April, 2008 at 3:51 pm
R.A.
Dear Professor Tao,
speaking about literature, there is a typo in the bibliography, in [10] the author should be Wesolowski or Weso{\l}owski if you want to use special Polish characters.
Thanks for a nice post
16 April, 2008 at 4:11 pm
Terence Tao
Thanks for the correction! I’ll pass it on to my co-author Van, who has the master copy of this paper.
25 August, 2008 at 5:38 am
nobody
Dear Prof. Tao,
do you know good descriptions or formulas for E(det X)^2, if X is a symmetric random Bernoulli (+1,-1) matrix? I have found
 which is rather complicated.
which is rather complicated.
25 August, 2008 at 1:10 pm
Terence Tao
Dear nobody,
I do not know of a simple closed form for this expression. You might try putting the reduced numerator and denominator of the first few elements of this sequence into the OEIS,
http://www.research.att.com/~njas/sequences/
and try your luck (or to add these sequences, if they are not already there).
22 March, 2011 at 11:18 am
Valiant’s Permanent Contributions « Gödel’s Lost Letter and P=NP
[…] Terry Tao and Van Vu have just proved some anti-concentration theorems—see their paper here for the […]
2 February, 2019 at 10:37 am
Konstantin Tikhomrov: The Probability that a Bernoulli Matrix is Singular | Combinatorics and more
[…] Here are related posts on Tao’s blog What’s New. A post on Tao’s Milliman’s lecture on the additive combinatorics and random matrices; On the permamnent of random Bernoulli matrix; […]