Below the fold, I am giving some sample questions for the 245B midterm next week. These are drawn from my previous 245A and 245B exams (with some modifications), and the solutions can be found by searching my previous web pages for those courses. (The homework assignments are, of course, another good source of practice problems.) Note that the actual midterm questions are likely to be somewhat shorter than the ones provided here (this is particularly the case for those questions with multiple parts). More info on the midterm can be found at the class web page, of course.
(These questions are of course primarily intended for my students than for my regular blog readers; but anyone is welcome to comment if they wish.)
Question 1. Let be a
-finite measure space, and let
be a signed
-finite measure. Show that the following are equivalent:
.
.
and
-a.e..
Question 2. Let be the real line with the Borel
-algebra, and let
be a
-finite unsigned measure. Show that it is not possible for counting measure
on the real line (restricted to
) to be absolutely continuous with respect to
, i.e.
.
Question 3. Let , let
be the Banach space of
power summable real sequences
with the usual
norm. For each natural number n, let
be the element of
consisting of the sequence which equals 1 at the
entry and 0 elsewhere, thus
when
and
otherwise. Let
be a sequence in a Banach space X.
- Show that there is at most one continuous linear transformation
with the property that
for all natural numbers n.
- If
, show that there exists a continuous linear transformation
with
for all natural numbers n if and only if the sequence
is bounded.
- If
, show that the uniqueness claim 1. can fail.
Question 4. Let W be a vector space, let A be an index set, and for every , let
be a subspace of W which is equipped with a norm
. Suppose that for each
, the normed vector space
is a Banach space. Assume also the following compatibility condition: if
and
is a sequence in
which converges in
norm to x and in
norm to y, then x is necessarily equal to y. Show that the space
equipped with the norm
is also a Banach space.
Question 5. Let H be a Hilbert space, and let
be an increasing sequence of closed subspaces of H. Let be the closure of the union of these subspaces; this is another closed subspace of H. Show that for any x in H, the sequence
converges in norm to
, where
is the orthogonal projection of x to V, and similarly for
.
Question 6. Let H be a Hilbert space, and let V be a closed subspace of H which is non-trivial (i.e. not equal to ). Let
be the orthogonal projection onto V.
- Show that
has operator norm 1.
- Show that
is self-adjoint, i.e.
.
- Show that
is idempotent, i.e.
.
- Conversely, if
is a self-adjoint idempotent continuous linear transformation of operator norm 1, show that
for some non-trivial subspace of H.
[Update, Feb 2: Question 4 corrected.]

7 comments
Comments feed for this article
25 January, 2009 at 8:34 pm
Anonymous
What’s this “ocunting measure” in question 2? Sounds dirty … [Fixed – T.]
30 January, 2009 at 9:48 am
Anonymous
For question 2, I also don’t understand the counting measure. So it lives on the sigma-algebra consisting of all the subsets of R, but niu is with Borel sigma-algebra. So they lives on different sigma-algebra.
30 January, 2009 at 9:57 am
Terence Tao
Fair enough; I intended to restrict counting measure to the Borel sigma algebra, and have now indicated this accordingly. (A measure on a sigma algebra can always be restricted to a sub-sigma algebra without difficulty.)
15 April, 2009 at 4:03 am
Anonymous
Dear professor!
I have a question which relate adjoint space. That is: ” Is![C^*[0,1]](https://s0.wp.com/latex.php?latex=C%5E%2A%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) linear isomorphism with
linear isomorphism with ![C[0,1]](https://s0.wp.com/latex.php?latex=C%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) ?”
?” ![C[0,1]](https://s0.wp.com/latex.php?latex=C%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is space of continous function in
is space of continous function in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) . If we choose inner product of
. If we choose inner product of ![C[0,1]](https://s0.wp.com/latex.php?latex=C%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) is
is ![: C[0,1]\longrightarrow\Bbb{R}](https://s0.wp.com/latex.php?latex=%3A+C%5B0%2C1%5D%5Clongrightarrow%5CBbb%7BR%7D&bg=ffffff&fg=545454&s=0&c=20201002) , by
, by  then
then ![C*[0,1] = C[0,1]](https://s0.wp.com/latex.php?latex=C%2A%5B0%2C1%5D+%3D+C%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) (isormophism)?
(isormophism)?
Thank you very much!
5 February, 2013 at 9:58 pm
Adam Azzam
I hate to be this comment; but I suppose that should also be non-trivial (so that the operator norm of the orthogonal projection is non-zero). [Corrected, thanks – T.]
should also be non-trivial (so that the operator norm of the orthogonal projection is non-zero). [Corrected, thanks – T.]
29 December, 2022 at 8:06 am
Aditya Guha Roy
Wow, I really like this collection of problems.
Do you also have a sample final term, or is it possible to share the actualy finals and actual mid term questions? I followed this series of lectures very closely, and would surely like to give the problems a shot.
(I’d soon post my solutions / attempts to solve these problems in a comment below.)
29 December, 2022 at 9:05 am
Aditya Guha Roy
Solution to Q6:
Part 1: Follows from Pythagorean theorem, and by taking a unit vector in the subspace.
Part 2: We have but the second term vanishes since the residual
but the second term vanishes since the residual  is orthogonal to every element of
is orthogonal to every element of  and hence in particular it is orthogonal to
and hence in particular it is orthogonal to  Similarly, one has
Similarly, one has 
Part 3: This follows from definition, since is the unique element of
is the unique element of 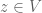 which minimizes
which minimizes  over all
over all 
Part 4: First of all notice that the range of a bounded idempotent operator is closed ( thus
thus  in particular
in particular  is in the range of
is in the range of 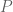 ).
). be the range of
be the range of  then one has (thanks to idempotent property)
then one has (thanks to idempotent property)  for all
for all  Now we have
Now we have  latex \langle x , y – Py \rangle = 0$ for all
latex \langle x , y – Py \rangle = 0$ for all  but this is equivalent to saying that
but this is equivalent to saying that 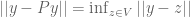 or in other words, that
or in other words, that  is the orthogonal projection of
is the orthogonal projection of 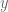 onto
onto  The claim follows.
The claim follows. 
Let
Solution to Q5: We will use the fact that projections are bounded linear operators. (One way to show this is to use Part 1 of Q6.) is a closed subspace of
is a closed subspace of  so
so  Thus it suffices to show that
Thus it suffices to show that 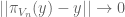 for all
for all 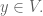
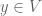 then there is a sequence
then there is a sequence 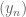 of points
of points 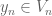 such that
such that  as
as 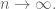 One has (by the triangle inequality):
One has (by the triangle inequality):
 using uniform boundedness principle the second term on the right hand side of the line of display goes to zero as
using uniform boundedness principle the second term on the right hand side of the line of display goes to zero as  and the other quantities also go to zero as
and the other quantities also go to zero as 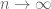 since
since 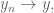 as
as 
To begin, notice that since
If
(PS: The comment above this one was made without reading that the solutions are already available; so I’ll post the solutions, only if I find signficantly distinct solutions to the remaining ones’.)