dWhen studying a mathematical space X (e.g. a vector space, a topological space, a manifold, a group, an algebraic variety etc.), there are two fundamentally basic ways to try to understand the space:
- By looking at subobjects in X, or more generally maps
from some other space Y into X. For iTnstance, a point in a space X can be viewed as a map from
to X; a curve in a space X could be thought of as a map from
to X; a group G can be studied via its subgroups K, and so forth.
- By looking at objects on X, or more precisely maps
from X into some other space Y. For instance, one can study a topological space X via the real- or complex-valued continuous functions
on X; one can study a group G via its quotient groups
; one can study an algebraic variety V by studying the polynomials on V (and in particular, the ideal of polynomials that vanish identically on V); and so forth.
(There are also more sophisticated ways to study an object via its maps, e.g. by studying extensions, joinings, splittings, universal lifts, etc. The general study of objects via the maps between them is formalised abstractly in modern mathematics as category theory, and is also closely related to homological algebra.)
A remarkable phenomenon in many areas of mathematics is that of (contravariant) duality: that the maps into and out of one type of mathematical object X can be naturally associated to the maps out of and into a dual object (note the reversal of arrows here!). In some cases, the dual object
looks quite different from the original object X. (For instance, in Stone duality, discussed in Notes 4, X would be a Boolean algebra (or some other partially ordered set) and
would be a compact totally disconnected Hausdorff space (or some other topological space).) In other cases, most notably with Hilbert spaces as discussed in Notes 5, the dual object
is essentially identical to X itself.
In these notes we discuss a third important case of duality, namely duality of normed vector spaces, which is of an intermediate nature to the previous two examples: the dual of a normed vector space turns out to be another normed vector space, but generally one which is not equivalent to X itself (except in the important special case when X is a Hilbert space, as mentioned above). On the other hand, the double dual
turns out to be closely related to X, and in several (but not all) important cases, is essentially identical to X. One of the most important uses of dual spaces in functional analysis is that it allows one to define the transpose
of a continuous linear operator
.
A fundamental tool in understanding duality of normed vector spaces will be the Hahn-Banach theorem, which is an indispensable tool for exploring the dual of a vector space. (Indeed, without this theorem, it is not clear at all that the dual of a non-trivial normed vector space is non-trivial!) Thus, we shall study this theorem in detail in these notes concurrently with our discussion of duality.
— Duality —
In the category of normed vector spaces, the natural notion of a “map” (or morphism) between two such spaces is that of a continuous linear transformation between two normed vector spaces X, Y. By Lemma 1 from Notes 3, any such linear transformation is bounded, in the sense that there exists a constant C such that
for all
. The least such constant C is known as the operator norm of T, and is denoted
or simply
.
Two normed vector spaces are equivalent if there is an invertible continuous linear transformation
from X to Y, thus T is bijective and there exist constants
such that
for all
. If one can take C=c=1, then T is an isometry, and X and Y are called isomorphic. When one has two norms
on the same vector space X, we say that the norms are equivalent if the identity from
to
is an invertible continuous transformation, i.e. that there exist constants
such that
for all
.
Exercise 1. Show that all linear transformations from a finite-dimensional space to a normed vector space are continuous. Conclude that all norms on a finite-dimensional space are equivalent.
Let denote the space of all continuous linear transformations from X to Y. (This space is also denoted by many other names, e.g.
,
, etc.) This has the structure of a vector space: the sum
of two continuous linear transformations is another continuous linear transformation, as is the scalar multiple
of a linear transformation.
Exercise 2. Show that with the operator norm is a normed vector space. If Y is complete (i.e. is a Banach space), show that
is also complete (i.e. is also a Banach space).
Exercise 3. Let X, Y, Z be Banach spaces. Show that if and
, then the composition
lies in
and
. (As a consequence of this inequality, we see that
is a Banach algebra.)
Now we can define the notion of a dual space.
Definition 1. (Dual space) Let X be a normed vector space. The (continuous) dual space
of X is defined to be
if X is a real vector space, and
if X is a complex vector space. Elements of
are known as continuous linear functionals (or bounded linear functionals) on X.
Remark 1. If one drops the requirement that the linear functionals be continuous, we obtain the algebraic dual space of linear functionals on X. This space does not play a significant role in functional analysis, though.
From Exercise 2, we see that the dual of any normed vector space is a Banach space, and so duality is arguably a Banach space notion rather than a normed vector space notion. The following exercise reinforces this:
Exercise 4. We say that a normed vector space X has a completion if
is a Banach space and X can be identified with a dense subspace of
(cf. Exercise 8 of Notes 5).
- Show that every normed vector space X has at least one completion
, and that any two completions
are isomorphic in the sense that there exists an isomorphism from
to
which is the identity on X.
- Show that the dual spaces
and
are isomorphic to each other.
The next few exercises are designed to give some intuition as to how dual spaces work.
Exercise 5. Let be given the Euclidean metric. Show that
is isomorphic to
. Establish the corresponding result for the complex spaces
.
Exercise 6. Let be the vector space of sequences
of real or complex numbers which are compactly supported (i.e. at most finitely many of the
are non-zero). We give
the uniform norm
.
- Show that the dual space
is isomorphic to
.
- Show that the completion of
is isomorphic to
, the space of sequences on
that go to zero at infinity (again with the uniform norm); thus, by Exercise 4, the dual space of
is isomorphic to
also.
- On the other hand, show that the dual of
is isomorphic to
, a space which is strictly larger than
or
. Thus we see that the double dual of a Banach space can be strictly larger than the space itself.
Exercise 7. Let H be a real or complex Hilbert space. Using the Riesz representation theorem for Hilbert spaces (Theorem 1 from Notes 5), show that the dual space is isomorphic (as a normed vector space) to the conjugate space
(see Example 8 from Notes 5), with an element
being identified with the linear functional
. Thus we see that Hilbert spaces are essentially self-dual (if we ignore the pesky conjugation sign).
Exercise 8. Let be a
-finite measure space, and let
. Using Theorem 1 from Notes 3, show that the dual space of
is isomorphic to
, with an element
being identified with the linear functional
. (The one tricky thing to verify is that the identification is an isometry, but this can be seen by a closer inspection of the proof of Theorem 1 from Notes 3. The
-finite hypothesis can be dropped when
, though we will not need this fact.)
One of the key purposes of introducing the notion of a dual space is that it allows one to define the notion of a transpose.
Definition 2. (Transpose) Let
be a continuous linear transformation from one normed vector space X to another Y. The transpose
of T is defined to be the map that sends any continuous linear functional
to the linear functional
, thus
for all
.
Exercise 9. Show that the transpose of a continuous linear transformation T between normed vector spaces is again a continuous linear transformation with
, thus the transpose operation is itself a linear map from
to
. (We will improve this result in Theorem 3 below.)
Exercise 10. An matrix A with complex entries can be identified with a linear transformation
. Identifying the dual space of
with itself as in Exercise 5, show that the transpose
is equal to
, where
is the transpose matrix of A.
Exercise 11. Show that the transpose of a surjective continuous linear transformation between normed vector spaces is injective. Show that the condition of surjectivity can be relaxed to that of having a dense image.
Remark 3. Observe that if and
are continuous linear transformations between normed vector spaces, then
. In the language of category theory, this means that duality
of normed vector spaces, and transpose
of continuous linear transformations, form a contravariant functor from the category of normed vector spaces (or Banach spaces) to itself.
Remark 4. The transpose of a continuous linear transformation
between complex Hilbert spaces is closely related to the adjoint
of that transformation, as defined in Exercise 15 of Notes 5, by using the obvious (antilinear) identifications between H and
, and between H’ and
. This is analogous to the linear algebra fact that the adjoint matrix is the complex conjugate of the transpose matrix. One should note that in the literature, the transpose operator
is also (somewhat confusingly) referred to as the adjoint of T. Of course, for real vector spaces, there is no distinction between transpose and adjoint.
— The Hahn-Banach theorem —
Thus far, we have defined the dual space , but apart from some concrete special cases (Hilbert spaces,
spaces, etc.) we have not been able to say much about what
consists of – it is not even clear yet that if X is non-trivial (i.e. not just
), that
is also non-trivial – for all one knows, there could be no non-trivial continuous linear functionals on X at all! The Hahn-Banach theorem is used to resolve this, by providing a powerful means to construct continuous linear functionals as needed.
Theorem 1. (Hahn-Banach theorem) Let X be a normed vector space, and let Y be a subspace of X. Then any continuous linear functional
on Y can be extended to a continuous linear functional
on X with the same operator norm; thus
agrees with
on Y and
. (Note: the extension
is, in general, not unique.)
We prove this important theorem in stages. We first handle the codimension one real case:
Proposition 1. The Hahn-Banach theorem is true when X, Y are real vector spaces, and X is spanned by Y and an additional vector v.
Proof. We can assume that v lies outside Y, since the claim is trivial otherwise. We can also normalise (the claim is of course trivial if
vanishes). To specify the extension
of
, it suffices by linearity to specify the value of
. In order for the extension
to continue to have operator norm 1, we require that
for all and
. This is automatic for t=0, so by homogeneity it suffices to attain this bound for
. We rearrange this a bit as
.
But as has operator norm 1, an application of the triangle inequality shows that the inf on the RHS is at least as large as the sup on the LHS, and so one can choose
obeying the required properties.
Corollary 1. The Hahn-Banach theorem is true when X, Y are real normed vector spaces.
Proof. This is a standard “Zorn’s lemma” argument. Fix Y, X, . Define a partial extension of
to be a pair
, where Y’ is an intermediate subspace between Y and X, and
is an extension of
with the same operator norm as
. The set of all partial extensions is partially ordered by declaring
if
contains
and
extends
. It is easy to see that every chain of partial extensions has an upper bound; hence, by Zorn’s lemma, there must be a maximal partial extension
. If
, we are done; otherwise, one can find
. By Proposition 1, we can then extend
further to the larger space spanned by
and v, a contradiction; and the claim follows.
Remark 5. Of course, this proof of the Hahn-Banach theorem relied on the axiom of choice (via Zorn’s lemma) and is thus non-constructive. It turns out that this is, to some extent, necessary: it is not possible to prove the Hahn-Banach theorem if one deletes the axiom of choice from the axioms of set theory (although it is possible to deduce the theorem from slightly weaker versions of this axiom, such as the ultrafilter lemma).
Finally, we establish the complex case by leveraging the real case.
Proof of Hahn-Banach theorem (complex case). Let be a continuous complex-linear functional, which we can normalise to have operator norm 1. Then the real part
is a continuous real-linear functional on Y (now viewed as a real normed vector space rather than a complex one), which has operator norm at most 1 (in fact, it is equal to 1, though we will not need this). Applying Corollary 1, we can extend this real-linear functional
to a continuous real-linear functional
on X (again viewed now just as a real normed vector space) of norm at most 1.
To finish the job, we have to somehow complexify to a complex-linear functional
of norm at most 1 that agrees with
on Y. It is reasonable to expect that
; a bit of playing around with complex linearity then forces
. (1)
Accordingly, we shall use (1) to define . It is easy to see that
is a continuous complex-linear functional agreeing with
on Y. Since
has norm at most 1, we have
for all
. We can amplify this by exploiting phase rotation symmetry, thus
for all
. Optimising in
we see that
has norm at most 1, as required.
Exercise 12. In the special case when X is a Hilbert space, give an alternate proof of the Hahn-Banach theorem using the material from Notes 5 that avoids Zorn’s lemma or the axiom of choice.
Now we put this Hahn-Banach theorem to work in the study of duality and transposes.
Exercise 13. Let be a continuous linear transformation which is bounded from below (i.e. there exists
such that
for all
); note that this ensures that X is equivalent to some subspace of Y. Show that the transpose
is surjective. Give an example to show that the claim fails if T is merely assumed to be injective rather than bounded from below. (Hint: consider the map
on some suitable space of sequences.) This should be compared with Exercise 11.
Exercise 14. Let x be an element of a normed vector space X. Show that there exists such that
and
. Conclude in particular that the dual of a non-trivial normed vector space is again non-trivial.
Given a normed vector space X, we can form its double dual : the space of continuous linear functionals on
. There is a very natural map
, defined as
(2)
for all and
. (This map is closely related to the Gelfand transform in the theory of operator algebras.) It is easy to see that
is a continuous linear transformation, with operator norm at most 1. But the Hahn-Banach theorem gives a stronger statement:
Theorem 2.
is an isometry.
Proof. We need to show that for all
. The upper bound is clear; the lower bound follows from Exercise 14.
Exercise 15. Let Y be a subspace of a normed vector space X. Define the complement of Y to be the space of all
which vanish on Y.
- Show that
is a closed subspace of
, and that
; (Compare with Exercise 13 from Notes 5.) In other words,
.
- Show that
is trivial if and only if Y is dense, and
if and only if Y is trivial.
- Show that
is isomorphic to the dual of the quotient space
(which has the norm
).
- Show that
is isomorphic to
.
From Theorem 2, every normed vector space can be identified with a subspace of its double dual (and every Banach space is identified with a closed subspace of its double dual). If is surjective, then we have an isomorphism
, and we say that X is reflexive in this case; since
is a Banach space, we conclude that only Banach spaces can be reflexive. From linear algebra we see in particular that any finite-dimensional normed vector space is reflexive; from Exercises 7, 8 we see that any Hilbert space and any
space with
on a
-finite space is also reflexive (and the hypothesis of
-finiteness can in fact be dropped). On the other hand, from Exercise 6 we see that the Banach space
is not reflexive.
An important fact is that is also not reflexive: the dual of
is equivalent to
, but the dual of
is strictly larger than that of
. Indeed, consider the subspace
of
consisting of bounded convergent sequences (equivalently, this is the space spanned by
and the constant sequence
). The limit functional
is a bounded linear functional on
, with operator norm 1, and thus by the Hahn-Banach theorem can be extended to a generalised limit functional
which is a continuous linear functional of operator norm 1. As such generalised limit functionals annihilate all of
but are still non-trivial, they do not correspond to any element of
.
Exercise 16. Let be a generalised limit functional (i.e. an extension of the limit functional of
of operator norm 1) which is also an algebra homomorphism, i.e.
for all sequences
. Show that there exists a unique non-principal ultrafilter
(as defined for instance in this blog post) such that
for all sequences
. Conversely, show that every non-principal ultrafilter generates a generalised limit functional that is also an algebra homomorphism. (This exercise may become easier once one is acquainted with the Stone-Čech compactification, as discussed for instance in this lecture, and which we will discuss later in this course. If the algebra homomorphism property is dropped, one has to consider probability measures on the space of non-principal ultrafilters instead.)
Exercise 17. Show that any closed subspace of a reflexive space is again reflexive. Also show that a Banach space X is reflexive if and only if its dual is reflexive. Conclude that if is a measure space which contains a countably infinite sequence of disjoint sets of positive finite measure, then
and
are not reflexive. (Hint: Reduce to the
-finite case.
will contain an isometric copy of
.)
Theorem 2 gives a classification of sorts for normed vector spaces:
Corollary 1. Every normed vector space X is isomorphic to a subspace of BC(Y), the space of bounded continuous functions on some bounded complete metric space Y, with the uniform norm.
Proof. Take Y to be the unit ball in , then the map
identifies X with a subspace of BC(Y).
Remark 6. If X is separable, it is known that one can take Y to just be the unit interval [0,1]; this is the Banach-Mazur theorem, which we will not prove here.
Next, we apply the Hahn-Banach theorem to the transpose operation, improving Exercise 9.
Theorem 3. Let
be a continuous linear transformation between normed vector spaces. Then
; thus the transpose operation is an isometric embedding of
into
.
Proof. By Exercise 9, it suffices to show that . Accordingly, let
be any number strictly less than
, then we can find
such that
. By Exercise 14 we can then find
such that
and
, and thus
. This implies that
; taking suprema over all
strictly less than
we obtain the claim.
If we identify X and Y with subspaces of and
respectively, we thus see that
is an extension of
with the same operator norm. In particular, if X and Y are reflexive, we see that
can be identified with T itself (exactly as in the finite-dimensional linear algebra setting).
— Variants of the Hahn-Banach theorem (optional) —
The Hahn-Banach theorem has a number of essentially equivalent variants, which also are of interest for the geometry of normed vector spaces.
Exercise 18. (generalised Hahn-Banach theorem) Let Y be a subspace of a real or complex vector space X, let be a sublinear functional on X (thus
for all non-negative c and all
, and
for all
), and let
be a linear functional on Y such that
for all
. Show that
can be extended to a linear functional
on X such that
for all
. Show that this statement implies the usual Hahn-Banach theorem. (Hint: adapt the proof of the Hahn-Banach theorem.)
Call a subset A of a real vector space V algebraically open if the sets are open in
for all
; note that every open set in a normed vector space is algebraically open.
Theorem 4. (Geometric Hahn-Banach theorem) Let A, B be convex subsets of a real vector space V, with A algebraically open. Then the following are equivalent:
- A and B are disjoint.
- There exists a linear functional
and a constant c such that
on A, and
on B. (Equivalently, there is a hyperplane separating A and B, with A avoiding the hyperplane entirely.)
If A and B are convex cones (i.e.
whenever
and
, and similarly for B), we may take c=0.
Remark 7. In finite dimensions, it is not difficult to drop the algebraic openness hypothesis on as long as one now replaces the condition
by
. However in infinite dimensions one cannot do this. Indeed, if we take
, let A be the set of sequences whose last non-zero element is strictly positive, and
consist of those sequences whose last non-zero element is strictly negative, then one can verify that there is no hyperplane separating
from
.
Proof. Clearly 2 implies 1; now we show that 1 implies 2. We first handle the case when A and B are convex cones.
Define a good pair to be a pair (A,B) where A and B are disjoint convex cones, with A algebraically open, thus (A,B) is a good pair by hypothesis. We can order if A’ contains A and B’ contains B. A standard application of Zorn’s lemma reveals that any good pair (A,B) is contained in a maximal good pair, and so without loss of generality we may assume that (A,B) is a maximal good pair.
We can of course assume that neither nor
is empty.
We now claim that is the complement of
. For if not, then there exists
which does not lie in either
or
. By the maximality of
, the convex cone generated by
must intersect
at some point, say
. By dilating
if necessary we may assume that
lies on a line segment between
and some point
in
. By using the convexity and disjointness of
and
one can then deduce that for any
, the ray
is disjoint from
. Thus one can enlarge
to the convex cone generated by
and
, which is still algebraically open and now strictly larger than
(because it contains
), a contradiction. Thus
is the complement of
.
Let us call a line in \emph{monochromatic} if it is entirely contained in
or entirely contained in
. Note that if a line is not monochromatic, then (because
and
are convex and partition the line, and
is algebraically open), the line splits into an open ray contained in
, and a closed ray contained in
. From this we can conclude that if a line is monochromatic, then all parallel lines must also be monochromatic, because otherwise we look at the ray in the parallel line which contains
and use convexity of both
and
to show that this ray is adjacent to a halfplane contained in
, contradicting algebraic openness. Now let
be the space of all vectors
for which there exists a monochromatic line in the direction
(including 0). Then
is easily seen to be a vector space;
since are non-empty,
is a proper subspace of
. On the other hand, if
and
are not in
, some playing around with the property that
and
are convex sets partitioning
shows that the plane spanned by
and
contains a monochromatic line, and hence some non-trivial linear combination of
and
lies in
. Thus
is precisely one-dimensional. Since every line with direction in
is monochromatic,
and
also have well-defined quotients
and
on this one-dimensional subspace, which remain convex (with
still algebraically open). But then it is clear that
and
are an open and closed ray from the origin in
respectively. It is then a routine matter to construct a linear functional
(with null space
) such that
,
; we leave the verification that this works as an exercise.
Exercise 19. Use the geometric Hahn-Banach theorem to reprove Exercise 18, thus providing a slightly different proof of the Hahn-Banach theorem. (It is possible to reverse these implications and deduce the geometric Hahn-Banach theorem from the usual Hahn-Banach theorem, but this is somewhat trickier, requiring one to fashion a norm out of the difference A-B of two convex cones.)
Exercise 20. (Algebraic Hahn-Banach theorem) Let V be a vector space over a field F, let W be a subspace of V, and let be a linear map. Show that there exists a linear map
which extends
.
Some further discussion of variants of the Hahn-Banach theorem (in the finite-dimensional setting) can be found at this blog post of mine.

56 comments
Comments feed for this article
26 January, 2009 at 3:01 pm
James
This is off, well not quite ‘off’, topic, but certainly out of the main focus…
I just watched my ex-college win convincingy on a UK quiz show called – not very suprisingly – ‘University Challenge’. (They trounced (365 to 20) the other team – hurah!) But one question they had was to name (I forget the exact words) but the name of the guy who created the most common integral used in most physics and engineering problems (to my dismay they didn’t know it was Riemann) then followed a question about which measure makes the Lesbesgue integral the same as the Riemann one (the answer apparently ‘Jordan’ – this I am not familiar with (and they also got it wrong))
However, my question is about the pronunciation of ‘Lesbesgue’, which was given by the quiz master as ‘le-bes-ke’ rather than the ‘le-bay-ge’ which I had always assumed – any official advice?
27 January, 2009 at 9:22 am
Eric
There are two Exercise 16s and the first one isn’t quite right. If by “generalized limit functional” you mean a norm 1 extension of the limit functional to all of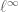 , then these are given just by elements of
, then these are given just by elements of  but by probability measures on it. Indeed, the full dual of
but by probability measures on it. Indeed, the full dual of 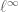 is the space of regular complex measures on
is the space of regular complex measures on 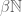 and functionals vanishing on
and functionals vanishing on 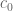 are measures supported on
are measures supported on  . However, if we restrict to functionals that are also multiplicative homomorphisms, we get only the point measures.
. However, if we restrict to functionals that are also multiplicative homomorphisms, we get only the point measures.
27 January, 2009 at 9:51 am
Terence Tao
Oops! Thanks for the correction.
31 January, 2009 at 3:10 am
Anonymous
proof of Proposition 1: y’ -> y [Corrected, thanks – T.]
4 February, 2009 at 1:26 pm
245B, Notes 9: The Baire category theorem and its Banach space consequences « What’s new
[…] was first proven by using the duality of the Hardy space and BMO (and by using Exercise 13 from Notes 6), and by using the fact that a function f is in if and only if f and Hf both lie in . From the […]
7 February, 2009 at 1:04 am
liuxiaochuan
Dear Professor Tao:
I don’t quite get the last two conslusions of Exercise 15, are there any typos there?
Xiaochuan
7 February, 2009 at 9:04 am
Terence Tao
Oops, there were several typos there. I’ve hopefully corrected them now…
8 February, 2009 at 8:14 pm
liuxiaochuan
Dear Professor Tao:
I have a question about the last exercise (Exercise 20). I want to know if I can simply define the extension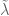 as
as 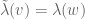 where w is the element in W such that
where w is the element in W such that  minimises the distance of v and W.
minimises the distance of v and W.
Xiaochuan
8 February, 2009 at 8:20 pm
Terence Tao
Dear Xiaochuan,
You can do this if V is a real Hilbert space and W is a closed subspace of V, but the hypotheses of the exercise are significantly more general than this. (In particular, the field F does not need to be real or complex.)
9 February, 2009 at 9:54 am
245B, Notes 10: Compactness in topological spaces « What’s new
[…] Recent Comments 245B, Notes 10: Comp… on 245B, Notes 9: The Baire categ…Raja on 254A, Lecture 8: The mean ergo…Boris on Upper and lower bounds for the…Jason Dyer on Upper and lower bounds for the…Jason Dyer on Upper and lower bounds for the…Gil on Upper and lower bounds for the…Michael Peake on Upper and lower bounds for the…Anonymous on Upper and lower bounds for the…Terence Tao on Random matrices: Universality …Stuart Anderson on Another advice page, and an op…Rajan on Proposed stimulus amendment el…Kristal Cantwell on Upper and lower bounds for the…Kristal Cantwell on Upper and lower bounds for the…Anonymous on Random matrices: Universality …Terence Tao on 245B, Notes 6: Duality and the… […]
16 February, 2009 at 7:28 am
实分析0-10 « Liu Xiaochuan’s Weblog
[…] 第六节讲的是对偶关系和Hahn-Banach定理。该定理的重要程度没法再强调了,在数学论文中,可以不用写参考文献直接使用。没有人不知道的。而关于对偶关系,前边我在帖子中写过一个利用弱*拓扑和Alaoglu定理来证明StoneCech紧化的帖子,跟ultrafilter有很大关系,取自John.B.Conway的书。本节中几个重点的例子也蛮重要的。还有就是最后一部分中Hahn-Banach定理的各种加强版。在这方面我手头最好的教材就是上面说的这本书了:A course in functional analysis GTM96. […]
3 March, 2009 at 8:15 am
-PRM-
Dear Pr. Tao,
As you wrote, a Banach space is reflexive iff the injective mapping is in fact an isomorphism. However, there exist Banach spaces X which are isometric to X” without being reflexive. I have run into an example but it was really complicated (the definition of the space itself took almost two pages !). Do you know any simple examples ?
is in fact an isomorphism. However, there exist Banach spaces X which are isometric to X” without being reflexive. I have run into an example but it was really complicated (the definition of the space itself took almost two pages !). Do you know any simple examples ?
Thanks
To Eric : Lebesgue, the s (yes, there’s only one !) isn’t pronounced, and it indeed sounds like “Luh – Bayg” ; if you wanna hear it in French, I think there’s an online video course by Pr. Jacques Vauthier about “mesure de Lebesgue” :)
4 March, 2009 at 8:28 am
PDEbeginner
Dear Prof. Tao,
I was a little confused on the second part of exercise 17. Do we need the disjoint sets sequence have measures uniformly bounded from below by some positive number?
If is a finite measure, is
is a finite measure, is  dual to
dual to 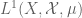 ? I tried to find the answer in Yosida’s book ‘Functional Analysis’, but it seems not to give it.
? I tried to find the answer in Yosida’s book ‘Functional Analysis’, but it seems not to give it.
Thanks a lot in advance!
4 March, 2009 at 9:04 am
Terence Tao
Dear PDEbeginner,
No, this is not necessary in order for to contain an isometric copy of
to contain an isometric copy of 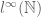 .
.
L^infty is indeed the dual of L^1 on finite measure spaces (or even sigma-finite spaces). This is essentially done in Theorem 1 of Notes 2 (though a little more work is needed to show that the identification of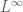 with
with  is an isomorphism). It’s also in Folland’s book on real analysis.
is an isomorphism). It’s also in Folland’s book on real analysis.
4 March, 2009 at 11:22 am
PDEbeginner
Dear Prof. Tao,
Thanks for your answer!
In my last question, I actually made a mistake. What I really want to ask is
If is finite, is
is finite, is 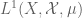 dual to
dual to  ?
?
Thanks!
4 March, 2009 at 11:51 am
Terence Tao
Dear PDEbeginner,
This is true when X is finite, but is false in general, because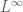 is often inseparable, while
is often inseparable, while  is often separable, and separable spaces cannot be the dual of inseparable spaces (Remark 6 of Notes 11). One can also often construct “explicit” elements of
is often separable, and separable spaces cannot be the dual of inseparable spaces (Remark 6 of Notes 11). One can also often construct “explicit” elements of 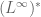 outside of
outside of  using ultrafilters or Hahn-Banach.
using ultrafilters or Hahn-Banach.
4 March, 2009 at 12:03 pm
PDEbeginner
Dear Prof. Tao,
I was still confused on the second part of excercise 17. It will imply that![(L^{\infty}([0,1], Leb))^{*} \neq L^1([0,1], Leb)](https://s0.wp.com/latex.php?latex=%28L%5E%7B%5Cinfty%7D%28%5B0%2C1%5D%2C+Leb%29%29%5E%7B%2A%7D+%5Cneq+L%5E1%28%5B0%2C1%5D%2C+Leb%29+&bg=ffffff&fg=545454&s=0&c=20201002) , but I have some problem to apply the arguments below Exercise 15 to prove it: Let us consider
, but I have some problem to apply the arguments below Exercise 15 to prove it: Let us consider ![L^{\infty}([0,1], Leb)](https://s0.wp.com/latex.php?latex=L%5E%7B%5Cinfty%7D%28%5B0%2C1%5D%2C+Leb%29&bg=ffffff&fg=545454&s=0&c=20201002) , take the disjoint sets as
, take the disjoint sets as  . Applying the similar arguments as in the
. Applying the similar arguments as in the  case, firstly construct the linear functional in some subspace of
case, firstly construct the linear functional in some subspace of ![L^{\infty}([0,1], Leb)](https://s0.wp.com/latex.php?latex=L%5E%7B%5Cinfty%7D%28%5B0%2C1%5D%2C+Leb%29+&bg=ffffff&fg=545454&s=0&c=20201002) (kind of step fundtion space, I think), then apply Hahn-Banach thm to extend this linear functional to
(kind of step fundtion space, I think), then apply Hahn-Banach thm to extend this linear functional to ![L^{1}([0,1], Leb)](https://s0.wp.com/latex.php?latex=L%5E%7B1%7D%28%5B0%2C1%5D%2C+Leb%29&bg=ffffff&fg=545454&s=0&c=20201002) . But then the arguments seem not to be applied due to the finiteness of the measure.
. But then the arguments seem not to be applied due to the finiteness of the measure.
Thanks!
4 March, 2009 at 1:29 pm
-PRM-
First possibility : the family (g_t)_{0 \leq t \leq 1}) where g_t=1_{[0,t]}, is uncountable, and d(g_t,g_s) is bounded from below, hence L^{\infty} is separable.
Second possibiility : define the linear functional \phi on C^0([0,1]) by \phi(f)=f(0), extend it to L^{\infty} with H.-B. and prove that the linear functional you obtained can’t be represented by a function in L^1.
26 June, 2010 at 9:28 am
The uncertainty principle « What’s new
[…] linear functionals; and so forth.) A fundamental connection between the two is given by the Hahn-Banach theorem (and its […]
13 February, 2011 at 9:04 pm
yucao
typo above exercise 1:
When one has two norms \|\|1 …
and the formula in exercise 1 is not showed
S+T: x \mapsto Sx+Tx
[Corrected, thanks – T.]
13 February, 2011 at 9:28 pm
yucao
Dear Prof. Tao,
I’m a little confused with the concept “isomorphic” here. Many books mentioned this concept only in a particular chapter instead of showing a big picture. It seems that “isomorphism” is a kind of “bijection” but it preserves many useful properties (generally what kind of properties?)with respect to the underlying mathematical structure. When talking about the dual space, some people use the concept “isometrically isomorphic”. So how do we know what kind of “bijection” is when we talk about “isomorphism” between two space or mathematical structure?
14 February, 2011 at 2:51 am
Terence Tao
In general, an isomorphism is a morphism from one space X to another Y which has an inverse
from one space X to another Y which has an inverse 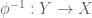 which is also a morphism. A morphism is a map which preserves all the structures of the space. For instance, if we are treating X and Y as groups, then a morphism is a group homomorphism; if we are treating them as rings, then a morphism is a ring homomorphism; if we are treating them as topological spaces, then a morphism is a continuous map; if we are treating them as topological groups, then a morphism is a continuous homomorphism, and so forth. Generally speaking, the “category” of spaces one is working in (e.g. vector spaces, groups, metric spaces, topological spaces, etc.) is clear from context; otherwise, one can specify the type of isomorphism being used more explicitly (e.g. Hilbert space isomorphism (i.e. unitary transformation), topological isomorphism (i.e. homeomorphism), etc.).
which is also a morphism. A morphism is a map which preserves all the structures of the space. For instance, if we are treating X and Y as groups, then a morphism is a group homomorphism; if we are treating them as rings, then a morphism is a ring homomorphism; if we are treating them as topological spaces, then a morphism is a continuous map; if we are treating them as topological groups, then a morphism is a continuous homomorphism, and so forth. Generally speaking, the “category” of spaces one is working in (e.g. vector spaces, groups, metric spaces, topological spaces, etc.) is clear from context; otherwise, one can specify the type of isomorphism being used more explicitly (e.g. Hilbert space isomorphism (i.e. unitary transformation), topological isomorphism (i.e. homeomorphism), etc.).
At a more abstract level, one can use the language of category theory to understand morphisms, isomorphisms, and related objects (e.g. functors, universal objects, direct sums and direct products) in a unified fashion, though it is probably best to first get a grip on concrete examples of categories (e.g. groups, vector spaces, etc.) before turning to abstract ones.
14 February, 2011 at 8:11 am
yucao
I noticed that when the base field is complex, is isomorphic to
is isomorphic to 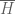 instead of
instead of  where
where  is a Hilbert space. Is this because
is a Hilbert space. Is this because  (
(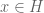 ) instead of
) instead of  ? Why the morphism between two complex vector space has to be defined in this way instead of being defined exactly as the morphism between the real ones, say
? Why the morphism between two complex vector space has to be defined in this way instead of being defined exactly as the morphism between the real ones, say  ? Is there any problem to do that?
? Is there any problem to do that?
14 February, 2011 at 8:31 am
Terence Tao
A morphism between complex vector spaces is indeed required to obey the homogeneity requirement . The canonical identification
. The canonical identification 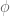 between
between  and
and  provided by the Riesz representation theorem however obeys the condition
provided by the Riesz representation theorem however obeys the condition  , so is an isomorphism between
, so is an isomorphism between  and
and 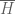 , rather than an isomorphism between
, rather than an isomorphism between  and
and  .
.
The spaces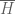 and
and  end up being isomorphic also (and so
end up being isomorphic also (and so  is also isomorphic to
is also isomorphic to  ), but the isomorphism is non-unique and non-canonical (it is not the one provided by the Riesz representation theorem).
), but the isomorphism is non-unique and non-canonical (it is not the one provided by the Riesz representation theorem).
11 March, 2011 at 9:33 am
Anonymous
When the underlying space is Hilbert space, is it possible to prove Theorem 3 in a simpler way?
11 March, 2011 at 11:02 am
Terence Tao
Well, Exercise 14 has a simple proof in this case (just set if
if  is non-zero, and
is non-zero, and 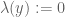 otherwise), so one can just insert this in place of Exercise 14 in the current proof of Theorem 3.
otherwise), so one can just insert this in place of Exercise 14 in the current proof of Theorem 3.
11 March, 2011 at 12:13 pm
Anonymous
When considering the “transpose” instead of “adjoint” operator, it seems that one can then use the Cauchy-Schwarz inequality:
11 March, 2011 at 12:20 pm
Terence Tao
One can certainly do this if one wishes, since the adjoint and transpose are essentially intertwined by the conjugation map from to
to 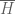 , which preserves norms.
, which preserves norms.
20 March, 2011 at 11:35 am
Anonymous
I have difficulty in following the proof in proposition 1. How does one get the LHS of the formula after “we rearrange this a bit as”, i.e.
 ?
?
20 March, 2011 at 11:45 am
Anonymous
I think the left hand side should be
 ?
?
20 March, 2011 at 3:28 pm
Terence Tao
Actually, I intended inside the infimum, although your expression would also work.
inside the infimum, although your expression would also work.
20 March, 2011 at 5:10 pm
Anonymous
Oops, I didn’t notice the errata of the book. (It should be in page 64 in the book I got, I don’t know why it is in page 56 in the errata webpage.) By and
and  one gets
one gets  . Then I think one may take the inf and sup one after another. Why the triangle inequality is needed here?
. Then I think one may take the inf and sup one after another. Why the triangle inequality is needed here?
20 March, 2011 at 8:10 pm
Terence Tao
Taking an inf and a sup consecutively only gives the desired inequality if one allows and
and  to vary independently of each other, in which case one needs to use the triangle inequality.
to vary independently of each other, in which case one needs to use the triangle inequality.
13 April, 2011 at 2:46 pm
Nathan Dypus
I wasn’t sure where to write this, but are the notes #5 and lower available anywhere?
13 April, 2011 at 9:35 pm
Terence Tao
https://terrytao.wordpress.com/category/teaching/245b-real-analysis/
(click on “previous entries” at the bottom of the page).
19 February, 2012 at 3:25 am
Rex
Concerning Exercise 1:
(A) Show that all linear transformations from a finite-dimensional space to a normed vector space are continuous.
(B) Conclude that all norms on a finite-dimensional space are equivalent.
While I can prove both parts individually, it is not clear to me how (A) can be used to derive (B).
Suppose V is our finite-dimensional vector space. As stated, no norm is specified for V, so one has to assume that the topology referenced in (A) is the standard Euclidean one.
Now suppose we are given two norms n, n’ on V and consider the map T: (V,n) —> (V,n’) given by the identity on the underlying set.
We would like to apply (A) here to conclude that T is continuous, but we can only do so if we assume that the topology on V arising from n is precisely the standard Euclidean topology, But I imagine this assumption is not permissible, since it essentially amounts to assuming (B).
19 February, 2012 at 8:27 am
Terence Tao
In (A), the intent is that the finite-dimensional space is equipped with an arbitrary norm.
19 September, 2014 at 3:47 am
André Caldas
Dear Professor Tao,
In the proof of the Geometric Hahn-Banach theorem, you take the “convex cone” generated by . Wouldn’t it be enough to take the generated “convex set”? Then you could avoid “dilating” the point
. Wouldn’t it be enough to take the generated “convex set”? Then you could avoid “dilating” the point 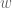 .
.
By the way, I didn’t really understood the part: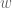 we may assume it lies on a line segment beween
we may assume it lies on a line segment beween  and some
and some 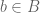 “.
“.
“by dilating
Thank you very much for your time! :-)
19 September, 2014 at 3:59 am
André Caldas
Sorry, I missed the correct definition of “good pairs”. :-(
They have to be convex cones to begin with. Otherwise, maximality will not make one the complement of the other.
Just ignore my last message.
Thank you!!!
24 March, 2015 at 5:09 am
Anonymous
To finish the job, we have to somehow complexify to a complex-linear functional
to a complex-linear functional  of norm at most 1
of norm at most 1
I think you mean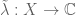 ?
?
[Corrected, thanks – T.]
24 March, 2015 at 10:25 am
Anonymous
I don’t understand the last step of the proof of the complex Hahn-Banach Theorem. The goal is to show that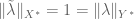 . How do we see that by ?
. How do we see that by ?
24 March, 2015 at 11:00 am
Terence Tao
See also the previous blog post https://terrytao.wordpress.com/2007/09/05/amplification-arbitrage-and-the-tensor-power-trick/ for more examples of the amplification trick.
24 March, 2015 at 10:45 am
Anonymous
Is the completeness assumption also needed in Exercise 14 in order to use the Hahn-Banach Theorem?
24 March, 2015 at 11:02 am
Terence Tao
The Hahn-Banach theorem does not require completeness.
24 March, 2015 at 12:01 pm
Anonymous
Ah, I see. Some books (e.g. Banach Algebra Techniques in Operator Theory by Douglas) put the extra assumption of completeness by assuming that space in the statement. It turns out that it is not needed at all.
4 October, 2015 at 5:51 pm
Anonymous
In this (http://mathoverflow.net/questions/80567/what-is-an-isomorphism-of-banach-spaces) question from MO, there are two definitions for isomorphism between two Banach spaces X and Y. Why in this note, the “isometry” one instead of the “linear homeomorphism” one is preferable?
[Both equivalence (i.e. linear homeomorphism) and isometry are used in this set of notes; the choice of reserving the latter rather than the former for “isomorphic” was largely a matter of personal preference. -T.]
5 October, 2015 at 6:33 am
Anonymous
When people talk about dual spaces, say, , it seems that isometry is used instead of linear homeomorphism. Are these two equivalence somehow the “same” when one wants to identify the dual space for some normed space?
, it seems that isometry is used instead of linear homeomorphism. Are these two equivalence somehow the “same” when one wants to identify the dual space for some normed space?
5 October, 2015 at 8:03 am
Terence Tao
It depends on the application. In many situations one is willing to lose a constant factor in the estimates and so identifying a space up to linear homeomorphism suffices. (For instance, this is usually what is done to identify the dual of a Sobolev space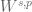 with
with  .) But if the stronger notion of an isometric identification is available (as is the case with
.) But if the stronger notion of an isometric identification is available (as is the case with 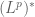 and
and 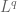 ), one may as well take advantage of it.
), one may as well take advantage of it.
10 October, 2015 at 1:13 pm
Anonymous
We know from the exercises that and
and  . Do you have a hint about what is
. Do you have a hint about what is  ?
?
[It’s pretty nasty; see Exercise 16. I think there is some description of this space in terms of something like finite measures on the Stone-Cech compactification of the natural numbers, but I forget the details. -T.]
6 March, 2016 at 1:52 pm
Anonymous
In the definition of double dual, why can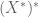 be defined as the algebraic dual of
be defined as the algebraic dual of 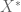 instead of the continuous dual (after putting a weak topology on
instead of the continuous dual (after putting a weak topology on 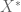 )?
)?
[This is a typo, now corrected. -T.]
7 March, 2016 at 10:39 am
Anonymous
By definition,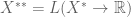 , the set of all the linear functionals from
, the set of all the linear functionals from 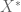 to
to 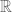 , not
, not 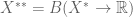 . In the proof of Theorem 2, what is the definition of
. In the proof of Theorem 2, what is the definition of  ?
?
7 March, 2016 at 12:41 pm
Anonymous
Ah, I was a little confused since the weak-* topology on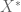 is not mentioned until much later on notes 11 hence I don’t see what it means by
is not mentioned until much later on notes 11 hence I don’t see what it means by  .
.
8 March, 2016 at 5:09 am
Terence Tao
27 October, 2016 at 7:08 pm
Anonymous
in exercise 6, what do you mean by “strictly larger”? i think they have the same cardinality. or you mean the “properly include”?
[I mean larger in the sense of proper set containment, yes. -T.]
16 January, 2019 at 8:43 am
245A: Problem solving strategies | What's new
[…] entire proof is basically “Apply Zorn’s lemma in the obvious fashion.” The Hahn-Banach theorem is a well known example of this, but there are many others (e.g. the proof of existence of […]
22 February, 2019 at 5:46 am
Thibaut
Does the axiom-of-choice-avoiding construction in exercise 12 (Hahn-Banach extension theorem in Hilbert-space, putting the Riesz representation theorem to good use) have a generalization to the version of the extension theorem where the sought-for linear functional has to remain below a sub-linear or convex function? (as in exercise 18)