[This post was typeset using a LaTeX to WordPress-HTML converter kindly provided to me by Luca Trevisan.]
Many properties of a (sufficiently nice) function are reflected in its Fourier transform
, defined by the formula
For instance, decay properties of are reflected in smoothness properties of
, as the following table shows:
| If |
then |
and this relates to… |
| Square-integrable | square-integrable | Plancherel’s theorem |
| Absolutely integrable | continuous | Riemann-Lebesgue lemma |
| Rapidly decreasing | smooth | theory of Schwartz functions |
| Exponentially decreasing | analytic in a strip | |
| Compactly supported | entire and at most exponential growth | Paley-Wiener theorem |
Another important relationship between a function and its Fourier transform
is the uncertainty principle, which roughly asserts that if a function
is highly localised in space, then its Fourier transform
must be widely dispersed in space, or to put it another way,
and
cannot both decay too strongly at infinity (except of course in the degenerate case
). There are many ways to make this intuition precise. One of them is the Heisenberg uncertainty principle, which asserts that if we normalise
then we must have
thus forcing at least one of or
to not be too concentrated near the origin. This principle can be proven (for sufficiently nice
, initially) by observing the integration by parts identity
and then using Cauchy-Schwarz and the Plancherel identity.
Another well known manifestation of the uncertainty principle is the fact that it is not possible for and
to both be compactly supported (unless of course they vanish entirely). This can be in fact be seen from the above table: if
is compactly supported, then
is an entire function; but the zeroes of a non-zero entire function are isolated, yielding a contradiction unless
vanishes. (Indeed, the table also shows that if one of
and
is compactly supported, then the other cannot have exponential decay.)
On the other hand, we have the example of the Gaussian functions ,
, which both decay faster than exponentially. The classical Hardy uncertainty principle asserts, roughly speaking, that this is the fastest that
and
can simultaneously decay:
Theorem 1 (Hardy uncertainty principle) Suppose that
is a (measurable) function such that
and
for all
and some
. Then
is a scalar multiple of the gaussian
.
This theorem is proven by complex-analytic methods, in particular the Phragmén-Lindelöf principle; for sake of completeness we give that proof below. But I was curious to see if there was a real-variable proof of the same theorem, avoiding the use of complex analysis. I was able to find the proof of a slightly weaker theorem:
Theorem 2 (Weak Hardy uncertainty principle) Suppose that
is a non-zero (measurable) function such that
and
for all
and some
. Then
for some absolute constant
.
Note that the correct value of should be
, as is implied by the true Hardy uncertainty principle. Despite the weaker statement, I thought the proof might still might be of interest as it is a little less “magical” than the complex-variable one, and so I am giving it below.
— 1. The complex-variable proof —
We first give the complex-variable proof. By dilating by
(and contracting
by
) we may normalise
. By multiplying
by a small constant we may also normalise
.
The super-exponential decay of allows us to extend the Fourier transform
to the complex plane, thus
for all . We may differentiate under the integral sign and verify that
is entire. Taking absolute values, we obtain the upper bound
completing the square, we obtain
for all . We conclude that the entire function
is bounded in magnitude by on the imaginary axis; also, by hypothesis on
, we also know that
is bounded in magnitude by
on the real axis. Formally applying the Phragmen-Lindelöf principle (or maximum modulus principle), we conclude that
is bounded on the entire complex plane, which by Liouville’s theorem implies that
is constant, and the claim follows.
Now let’s go back and justify the Phragmén-Lindelöf argument. Strictly speaking, Phragmén-Lindelöf does not apply, since it requires exponential growth on the function , whereas we have quadratic-exponential growth here. But we can tweak
a bit to solve this problem. Firstly, we pick
and work on the sector
Using (2) we have
Thus, if , and
is sufficiently close to
depending on
, the function
is bounded in magnitude by
on the boundary of
. Then, for any sufficiently small
,
(using the standard branch of
on
) is also bounded in magnitude by
on this boundary, and goes to zero at infinity in the interior of
, so is bounded by
in that interior by the maximum modulus principle. Sending
, and then
, and then
, we obtain
bounded in magnitude by
on the upper right quadrant. Similar arguments work for the other quadrants, and the claim follows.
— 2. The real-variable proof —
Now we turn to the real-variable proof of Theorem 2, which is based on the fact that polynomials of controlled degree do not resemble rapidly decreasing functions.
Rather than use complex analyticity , we will rely instead on a different relationship between the decay of
and the regularity of
, as follows:
Lemma 3 (Derivative bound) Suppose that
for all
, and some
. Then
is smooth, and furthermore one has the bound
for all
and every even integer
.
Proof: The smoothness of follows from the rapid decrease of
. To get the bound, we differentiate under the integral sign (one can easily check that this is justified) to obtain
and thus by the triangle inequality for integrals (and the hypothesis that is even)
On the other hand, by differentiating the Fourier analytic identity
times at
, we obtain
expanding out using Taylor series we conclude that
◻
Using Stirling’s formula , we conclude in particular that
for all large even integers (where the decay of
can depend on
).
We can combine (3) with Taylor’s theorem with remainder, to conclude that on any interval , we have an approximation
where is the length of
and
is a polynomial of degree less than
. Using Stirling’s formula again, we obtain
Now we apply a useful bound.
Lemma 4 (Doubling bound) Let
be a polynomial of degree at most
for some
, let
be an interval, and suppose that
for all
and some
. Then for any
we have the bound
for all
and for some absolute constant
.
Proof: By translating we may take ; by dilating we may take
. By dividing
by
, we may normalise
. Thus we have
for all
, and the aim is now to show that
for all
.
Consider the trigonometric polynomial . By de Moivre’s formula, this function is a linear combination of
for
. By Fourier analysis, we can thus write
, where
Since is bounded in magnitude by
, we conclude that
is bounded in magnitude by
. Next, we use de Moivre’s formula again to expand
as a linear combination of
and
, with coefficients of size
; expanding
further as
, we see that
is a polynomial in
with coefficients
. Putting all this together, we conclude that the coefficients of
are all of size
, and the claim follows. ◻
Remark 1 One can get slightly sharper results by using the theory of Chebyshev polynomials. (Is the best bound for
known? I do not know the recent literature on this subject. I think though that even the sharpest bound for
would not fully recover the sharp Hardy uncertainty principle, at least with the argument given here.)
We return to the proof of Theorem 2. We pick a large integer and a parameter
to be chosen later. From (4) we have
for , and some polynomial
of degree
. In particular, we have
for . Applying Lemma 4, we conclude that
for . Applying (4) again we conclude that
for . If we pick
for a sufficiently small absolute constant
, we conclude that
(say) for . If
for large enough
, the right-hand side goes to zero as
(which also implies
), and we conclude that
(and hence
) vanishes identically.

24 comments
Comments feed for this article
18 February, 2009 at 11:07 am
sjt
This new LaTeX-to-HTML converter doesn’t make alt text for its images, which is very unfriendly.
18 February, 2009 at 11:50 am
luca
It’s WordPress that has stopped providing alt text for the latex formulas. (The alt text is missing from the other posts, and in all other WordPress.com blogs too.)
19 February, 2009 at 6:13 am
Stones Cry Out - If they keep silent… » Things Heard: e55v4
[…] Uncertainty. […]
19 February, 2009 at 8:47 am
sjt
luca: “It’s WordPress that has stopped providing alt text for the latex formulas.” [not the new LaTeX-to-HTML converter]
My mistake. (Why on earth would they do that?!)
19 February, 2009 at 8:50 am
dweebydoofus
Hi Dr. Tao
do you think that Luca Trevisan would be interested in making this LaTeX to WordPress-HTML converter available to more users?
Thanks
19 February, 2009 at 9:39 am
dweebydoofus
By the way: Lemma 4 has a formula that doesn’t parse.
21 February, 2009 at 4:28 am
Pedro Lauridsen Ribeiro
Dear Prof. Tao,
There’s a related result, which seems to go back to Schrödinger (1926): the only minimisers of Heisenberg’s uncertainty principle are precisely the Gaussians (up to scaling, translation and modulation; I’m not sure if Schrödinger proved the “only” part). In quantum mechanics, these are called coherent states, although this name came much later (I think it was given by Klauder in the sixties).
21 February, 2009 at 7:02 am
Tom Jones
Dear Terry,
I was just wondering: What is your favorite movie? Because in the Tomb Raider post you mentioned that you played this game when you were younger. But do you like the movies today?
Thanks
21 February, 2009 at 1:15 pm
Fabrice Planchon
you may want to have a look at Bruno Demange’s PhD thesis, which has some interesting generalizations of Hardy’s theorem (building up on a theorem by Beurling). Still complex analysis, tho. A PDE oriented perspective may be found in a recent paper by Kenig-Ponce-Vega, and this is real analysis ;-)
Click to access DemangeTHE.pdf
http://arxiv.org/abs/0802.1608
21 February, 2009 at 1:59 pm
Converting LaTeX to WordPress « in theory
[…] Tao has tested it on a couple of posts. Thanks to his feedback, the current version, while surely bug-filled and very limited, is stable […]
23 February, 2009 at 12:36 am
Philippe Jaming
Hi Terry,
thanks for this post. If I remember well, there was a similar proof of Hardy’s Uncertainty Principle (UP) in Thangavelu’s book on the subject. A real variable proof would also help to get some progress on versions of Hardy’s UP for (say) the Heisenberg group, that would characterize the heat kernel (the natural analogue of gaussians). This was, I believe,
one of Thangavelu’s motivation.
I would also like to mention that there is a proof of Hardy’s UP du to B. Demange that works in the distributional setting (if f is a tempared distribution such that and
and  are also tempered distributions, then
are also tempered distributions, then  where P is a polynomial). This relies on transforming the problem into a complex analysis one via the Bargman transform and Phragmen Lindelöf. Demange’s result generalizes several extensions of Hardy’s UP most notably Beurling-Hörmander’s version of the UP (and the extension thereoff by Bonami-Demange and myself in 2003). He’s proof
where P is a polynomial). This relies on transforming the problem into a complex analysis one via the Bargman transform and Phragmen Lindelöf. Demange’s result generalizes several extensions of Hardy’s UP most notably Beurling-Hörmander’s version of the UP (and the extension thereoff by Bonami-Demange and myself in 2003). He’s proof
should appear soon in Memoires de la Société Math. Française
(as far as I know).
Finally, there is a series of recent papers by L. Escauriaza, C.E. Kenig, G. Ponce, L. Vega (sorry if I forget somebody) on the UP from the PDE
point of view (Shrödinger equation) that mainly relies on real analysis too.
Best regards
Philippe
26 March, 2009 at 7:17 pm
Well, there’s a comparison I didn’t expect to see… « Feed The Bears
[…] Tao, who amongst other things is a harmonic analyst, wrote a post a few weeks ago thinking about a similar question. Of course he thinks about it in a much deeper way, with much more advanced technology, and actually […]
6 April, 2010 at 6:52 am
Kaveh Khodjasteh
I keep coming back to this post because I think it must have to do with a problem that has occupied my mine for a long time. In particular, what triggered my attention was Lemma 3. Unfortunately I cannot use it because it holds only (?) for even order derivatives. Is that the case?
The problem I am talking here appears here:
http://mathoverflow.net/questions/16771/lower-bounds-on-truncated-fourier-transform-of-functions-of-constant-modulus-an
7 April, 2010 at 10:09 am
Yashar
Good to see you at Terry’s blog Kaveh!
25 June, 2010 at 6:44 pm
The uncertainty principle « What’s new
[…] formalisations of this principle, most famously the Heisenberg uncertainty principle and the Hardy uncertainty principle – but in many situations, it is the heuristic formulation of the principle that is more […]
15 September, 2014 at 4:38 am
wilsonofgordon
Prof. Tao (which occured in the complex analytical proof of the Hardy principle) have a minus sign? Doesn’t that make the first exponent have positive real part and diverge as z tends infinity? (I’m really new to wordpress and I’m sorry I dont know how to typeset LaTeX properly here so sorry.)
(which occured in the complex analytical proof of the Hardy principle) have a minus sign? Doesn’t that make the first exponent have positive real part and diverge as z tends infinity? (I’m really new to wordpress and I’m sorry I dont know how to typeset LaTeX properly here so sorry.)
Why does the exponent of the function
[Sorry, that was a sign error, now fixed – T.]
21 September, 2016 at 12:10 pm
Anonymous
Dear Prof. Tao,
Could you please explain to me what does you C on lemma 4 depend on ?
Thank you
[As stated in the lemma, C is an absolute constant (it can probably be conservatively taken to be something like 10, though I have not attempted to compute it explicitly.) -T.]
28 December, 2017 at 10:49 am
Uncertainty principle – Relationship of relationship
[…] pdf version is Uncertainty principle. The nice note of terrence tao seems given a nice answer for the problem […]
23 August, 2018 at 7:18 am
Ivo
There is a small typo (dx –> d\xi) towards the top:
<<>>
[Corrected, thanks -T.]
18 November, 2018 at 11:52 am
ss nn
Dear Prof. Tao,
Could you please explain why using Stirling’s formula after lemma 3 we get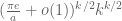
instead of ?
?
If I am not mistaken,
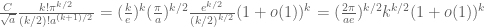
Thanks
[This was a typo, now corrected -T]
27 April, 2020 at 3:09 pm
Rex
Does the result that a nonzero function cannot have both compact support and compact Fourier support extend to higher dimensions?
27 April, 2020 at 4:58 pm
Terence Tao
Yes, because in any dimension the Fourier transform of an (absolutely integrable) function of compact support is real analytic in all variables, and this class of functions enjoys the unique continuation property.
27 April, 2020 at 8:13 pm
Rex
Does this mean that the open sets in the family
in the family  for decoupling estimates should always be unbounded, because we are using test functions which are smooth with compact support?
for decoupling estimates should always be unbounded, because we are using test functions which are smooth with compact support?
[That was a typo; the Schwartz class should have been used instead. -T]
12 July, 2022 at 3:50 am
Uncertainty principle - Relationship of relationship
[…] pdf version is Uncertainty principle. The nice note of terrence tao seems given a nice answer for the problem […]