Van Vu and I have just uploaded to the arXiv our paper “Random matrices: The distribution of the smallest singular values“, submitted to Geom. Func. Anal.. This paper concerns the least singular value of a random
matrix
with iid entries, which for simplicity we will take to be real (we also have analogues for complex random matrices), with mean zero and variance one. A typical model to keep in mind here is the Bernoulli model, when each
is equal to +1 or -1 with an equal probability of each, while a privileged role will be planed by the gaussian model, when each
is given the standard gaussian distribution.
The distribution of the least singular value , which is of importance in smoothed analysis and also has intrinsic interest within the field of random matrices, has been intensively studied in recent years. For instance, in the Bernoulli case, there have been several recent papers on the singularity probability
; it is not hard to obtain a lower bound of
, and this is conjectured to be the correct asymptotic. The best upper bound so far is by Bourgain, Vu, and Wood, who obtain
.
Upper and lower tail bounds have also been obtained, starting with the breakthrough paper of Rudelson (building upon some earlier work on rectangular matrices by Litvak, Pajor, Rudelson, and Tomczak-Jaegermann), with subsequent papers by Van and myself, by Rudelson, and also by Rudelson and Vershynin. To oversimplify somewhat, the conclusion of this work is that the least singular value has size comparable to
with high probability. The techniques are based in part on inverse Littlewood-Offord theorems.
However, in the case of the gaussian ensemble, we know more than just the expected size of the least singular value; we know its asymptotic distribution. Indeed, it was shown by Edelman in this case that one has
(1)
for any fixed . This computation was highly algebraic in nature, relying on special identities that are available only for extremely symmetric random matrix ensembles, such as the gaussian random matrix model; in particular, it is not obvious at all that the Bernoulli ensemble necessarily obeys the same distribution as the gaussian one. Nevertheless, motivated in part by this computation, Spielman and Teng conjectured that the bound
should hold for some for, say, the Bernoulli ensemble. This conjecture was verified up to losses of a multiplicative constant by Rudelson and Vershynin.
The main result of our paper is to show that the distribution of the least singular value is in fact universal, being asymptotically the same for all iid (real) random matrix models with the same mean and variance, and with a sufficiently high number of moment conditions. In particular, the asymptotic (1) for the gaussian ensemble is also true for the Bernoulli ensemble. Furthermore the error term o(1) can be shown to be of the shape for some c > 0, which in turn confirms the Spielman-Teng conjecture (without a loss of constant) in the polynomial size regime
for some
. We also have some further results for other low singular values (e.g.
for fixed k) but they are harder to state, and we will not do so here.
To our knowledge, this is the first universality result for the “hard edge” of the spectrum (i.e. the least few singular values) for iid square matrix models. [For rectangular matrices, where the hard edge is bounded away from zero, universality was recently established by Feldheim and Sodin.] The bulk distribution for the singular values of such matrices has been known for some time (it is governed by the famous Marchenko-Pastur law), while the distribution at the “soft edge” of the spectrum (i.e. the largest few singular values) was established to be universal by Soshnikov (here the distribution is governed by the Tracy-Widom law for the top singular value, and by the Airy kernel for the next few singular values). Both of these results are basically obtained by the moment method (or close relatives of this method, such as the resolvent method). However, the moment method is not effective for discerning the hard edge of the spectrum, since the singular values here are very small compared with the bulk and so have a negligible influence on the moments. [In the rectangular case, where the hard edge is bounded away from zero, the moment method becomes available again, though the application of it is quite delicate; see the Feldheim-Sodin paper for details.] Instead, we proceed by observing a certain central limit theorem type behaviour for the geometry of the columns of , which is enough to give us the desired universality; more details on the proof lie below the fold.
— Proof strategy —
As with our earlier paper on the universality of the circular law, we do not attempt to prove (1) for general ensembles such as the Bernoulli ensemble (say) directly. Instead, we use a Lindeberg-style approach to separate the analytic difficulties from the algebraic ones by first comparing the least singular value of a Bernoulli matrix
with the corresponding least singular value
of a gaussian matrix
. If we can show a universality property
(2)
where we use to denote the informal statement that two random variables X, Y have asymptotically the same distribution (after appropriate renormalisation, and in some appropriate metric), then the claim (1) for the Bernoulli matrix
will then follow from the existing work of Edelman establishing (1) for the gaussian matrix
.
To establish the approximation (2) for the least singular value, the first thing we do is flip it around, so that we now seek an approximation for the largest singular value for the inverse matrices:
. (3)
Experience has shown that largest singular values are easier to compute than least singular values (for instance, they are the same thing as the operator norm and can be computed by, say, the power method). But there is a huge price to pay: whereas the matrices had iid entries and were thus tractable to manipulate, the inverse matrices
have highly coupled entries and are quite difficult to manipulate; in particular, it is not easy at all to control high moments of
. So the moment method does not work terribly well (although the second moment of
is computable, and already useful – we used this “negative second moment identity” to good effect in our earlier paper).
So we do something else. It turns out that the singular values of tend to be spaced apart with spacing about
; in particular,
is heuristically about
. (This intuition is supported by the Marchenko-Pastur law, and is also backed up by the tail estimates of Rudelson and Vershynin mentioned earlier.) Inverting this, we see that the
largest singular value of
should be about
. Thus we see that (after dividing out the normalising factor
) the matrix
should behave like a compact operator; its singular values decay to zero at a noticeable rate. In particular,
should behave approximately like a finite rank matrix. (More accurately, “finite” should be “bounded uniformly in n”.)
At this point, we use the philosophy from the property testing literature for finite rank matrices, which tells us that statistics of large finite rank matrix (and in particular, its largest eigenvalue) often can be computed accurately from a small random sample of that matrix. Indeed, if we pick a small integer s (in practice for some small
, and let
be the
matrix formed by taking s rows of
at random (actually, given the iid nature of
, we can just take the first s rows), then we expect (from the approximate finite rank nature of
)
.
It turns out that one can justify this by an application of the moment method, coupled with some estimates on the size of the rows of which can be obtained variants of the machinery used in previous papers (in particular, we need some new estimates on distances between random vectors and random hyperplanes).
Of course, everything we say about the Bernoulli ensemble has counterparts for the gaussian ensemble, and so we are reduced to showing that
.
To show this, we invert again, viewing the largest singular value of as the least non-trivial singular value of the (pseudo-)inverse of B(M_n). Indeed, some elementary linear algebra tells us that
where the matrix
is formed by projecting the first s columns
of M onto the s-dimensional space V defined as the orthocomplement of the span of the remaining columns
, and then expressing those vectors using some arbitrarily chosen orthonormal basis for V. [This fact is perhaps most familiar in the simple case s=1, when it is saying that the size of a row of
is the reciprocal of the distance between the corresponding column of
to the hyperplane spanned by the other columns of
.]
Of course, we have similar computations for the gaussian ensemble; so we are now reduced to showing that
.
It looks like we are more or less back to where we started (cf. (2)), but with matrices instead of
matrices. Indeed, the projected gaussian matrix
can easily be checked to have exactly the same distribution as the
gaussian matrix
, basically because the projection of an n-dimensional gaussian random vector to an s-dimensional subspace is an s-dimensional gaussian vector.
But now for the punchline: the projected Bernoulli matrix also has distribution very close to the gaussian matrix
, because the projection of a n-dimensional Bernoulli random vector to a (sufficiently non-degenerate) s-dimensional subspace also behaves like an s-dimensional gaussian vector. This is basically a consequence of the central limit theorem; for technical reasons we need a modification of the Berry-Esseén version of this theorem. One has to show that the space V is sufficiently non-degenerate, but this can be done by a modification of techniques already in the literature (specifically, we rely on Talagrand’s inequality and a quantitative form of the Marchenko-Pastur law). Once this is done, the claim follows from the stability properties of
(specifically, we use the Hoffman-Weilandt inequality).

16 comments
Comments feed for this article
4 March, 2009 at 9:15 am
Mark Meckes
Have you considered whether the Lindeberg-style approach of this and your other recent paper could provide simpler proofs of Soshnikov’s universality results for the largest eigenvalues/singular values? Or maybe the invocation of the moment method in the “property testing” part of your proof would just lead one to repeat large parts of Soshnikov’s proof, or something like it?
Incidentally, explicit statements of still more general versions of Talagrand’s concentration inequality than your Theorem E.2 appear in the literature, for example Theorem 9 here or Corollary 4 here. In slightly disguised form, it’s even in Ledoux’s book as Theorem 4.15, which originally appeared as Theorem 3 here.
4 March, 2009 at 9:46 am
R.A.
Dear Prof. Tao,
is your result related to a recent work by Ohad N. Feldheim, and Sasha Sodin, available at http://arxiv.org/abs/0812.1961 ?
4 March, 2009 at 9:59 am
Terence Tao
Dear RA,
Thanks for pointing out this paper (someone else just drew it to my attention also). The Feldheim-Sodin paper establishes a similar result to ours, but for rectangular matrices (with aspect ratio bounded away from 1) rather than square ones. In that setting, the hard edge of the spectrum is bounded away from zero and the moment method becomes (in principle) applicable, although it is extremely delicate (the Feldheim-Sodin paper is 51 pages long). In our setting the hard edge is at zero and we cannot use the moment method directly, so our techniques are rather different. But certainly the conclusions are in the same spirit. (We’ll revise the paper shortly to reflect this and some other references that have been drawn to our attention.)
4 March, 2009 at 10:03 am
skoro
Nice paper! At a first look, the ”property testing” argument
seems very similar in spirit to the observation made by :
http://arxiv.org/abs/0808.2521
4 March, 2009 at 3:09 pm
Terence Tao
Mark: Thanks for the references! Actually we cite Ledoux’ book (Corollary 4.10) already for this result, though there is the rather trivial distinction that we are dealing with complex random variables rather than real ones.
Our arguments rely to a large extent on the fact that M^{-1} is effectively behaving like a bounded rank matrix, so that it its largest singular value can be easily estimated by a sampling argument. In contrast, M itself does not behave like a finite rank matrix, but if there was some way to transform M so that the largest few singular values dominated and everything else became small (much like the inverse map brings the least singular values into a position of dominance) then perhaps one could do something similar. One can of course take high powers of M or MM^* to achieve this, but then this is nothing more than the classical moment method, which I believe is what Soshnikov’s method is based on. (Our property testing lemma uses only the fourth moment; in our essentially finite rank setting, this already gives enough concentration of measure for our application, which is fortunate as higher moments of M^{-1} beyond the fourth turn out to be rather difficult to compute.)
Dear skoro: Thanks for the interesting link! In that paper the authors show that a random submatrix of a given matrix has a universal spectral distribution even if the original matrix is not low rank – but it seems that they do not relate this distribution to the spectrum of the original matrix, so it isn’t quite the same sort of property testing phenomenon we exploit in our own work. Still, it certainly is part of the same wider body of ideas.
4 March, 2009 at 4:47 pm
Mark Meckes
Terry: The results I mentioned actually cover the case of complex random variables and more – you can replace them with bounded random vectors in an arbitrary collection of normed vector spaces.
Soshnikov’s method is as you say based on the classical moment method. What I find interesting is that his papers, like yours, don’t prove the limit results directly, but instead show that a large random matrix behaves in certain ways like a large Gaussian random matrix, and then cite the known limit results in the Gaussian setting. That’s what made me wonder if a Lindeberg-type approach might give an easier proof than the very difficult enumerative combinatorics in Soshnikov’s papers.
Regarding the paper of Chatterjee and Ledoux pointed out by skoro, the authors actually remark (rather in passing) that their result indeed does not in general relate well to the spectrum of the original matrix.
6 March, 2009 at 2:51 pm
A semana nos arXivs… « Ars Physica
[…] Random matrices: The distribution of the smallest singular values […]
15 April, 2009 at 1:30 pm
wdf
Dear Dr. Tao,
What about the random matrix (n by m) with its elements, iid, uniformly distribution on [-1,1]? esp for large n>>m, Is the spectral norm of its pseudo inverse very small? I tested in matlab.
Thanks.
24 April, 2009 at 8:18 am
Mark Meckes
Terry: Is there a reason I’m not seeing that for your Proposition 3.4 (Berry-Esseen theorem for frames) you can’t just use an off-the-shelf result like those in (I think) chapter 15 of this book for example?
27 April, 2009 at 10:34 am
Terence Tao
Dear Mark,
That’s quite likely. I think when we found out we needed a multidimensional Berry-Esseen theorem, it was quicker to just write down a statement and proof of the type of result we needed than to hunt in the literature for a close enough match. But it’s certainly a standard result; that’s one reason why it’s in an appendix rather than in the main text. :)
29 May, 2009 at 7:50 am
Terence Tao
Dear Mark,
We finally got around to taking a look at the Berry-Esseen result you indicated. It is indeed very close to what we need, but unfortunately if one applies it directly there is an exponential loss in the dimension. For our applications, the dimension is a small power of , so we needed a variant of the Berry-Esseen theory that only loses polynomial factors in the dmiension.
, so we needed a variant of the Berry-Esseen theory that only loses polynomial factors in the dmiension.
30 May, 2009 at 9:53 am
Mark Meckes
Terry,
Ah, I see. Well, there’s more recent literature out there on the dependence on the dimension in multivariate Berry-Esseen theorems, but in that case I’m sure you’re right that it’s easier just to prove what you needed.
28 August, 2010 at 9:07 pm
Sujit
Dear Terry,
Using dimensional analysis, we can easily rule out certain Sobolev embeddings as you discussed in 245C Notes 4 and in your notes on tensor power trick. Many of the estimates in random matrix theory seems out of the blue. Can some of these estimates, both for the square matrix and rectangular matrix case, be quickly derived as necessary condition by off the shelf dimensional analysis heuristics? Thanks.
28 August, 2010 at 9:14 pm
Sujit
In other words, what kind of scaling heuristic can one use (if at all) to guess tail bound inequalities rather than complete integral inequalities as in Sobolev embeddings?
30 August, 2010 at 8:16 am
Terence Tao
Dimensional analysis is of limited value for random matrix theory since there are multiple scales in play, although if one adopts the heuristic that the tensor product of an and an
and an 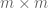 matrix behaves like a random
matrix behaves like a random  matrix, one can at least obtain the prediction that many key statistics of a matrix (e.g. largest and smallest singular values) should behave according to a power law in the dimension
matrix, one can at least obtain the prediction that many key statistics of a matrix (e.g. largest and smallest singular values) should behave according to a power law in the dimension  . However this argument does not reveal what the exponent of such power laws should be.
. However this argument does not reveal what the exponent of such power laws should be.
Nevertheless, there are still ad hoc heuristics available. For instance, there is a close analogy between the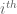 largest singular value of a matrix, and the distance
largest singular value of a matrix, and the distance  between the
between the 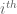 row
row 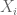 and the span
and the span  of the preceding
of the preceding 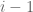 rows (assuming the rows are “generically ordered” in some sense). Using this together with concentration of measure heuristics, one can arrive at such conclusions as that the least singular value of a
rows (assuming the rows are “generically ordered” in some sense). Using this together with concentration of measure heuristics, one can arrive at such conclusions as that the least singular value of a  matrix should be comparable to
matrix should be comparable to  .
.
Another common way to obtain heuristics is to work with a tractable explicit model, such as GUE, and assume as a universality heuristic that other random matrix models with the same basic statistics as GUE (e.g. mean and variance of the entries) will enjoy similar behaviour.
30 November, 2010 at 3:05 pm
PKG
Can we apply any of this theory to determine the distribution of the (induced) -norm of a random square matrix?
-norm of a random square matrix?