A key theme in real analysis is that of studying general functions or
by first approximating them by “simpler” or “nicer” functions. But the precise class of “simple” or “nice” functions may vary from context to context. In measure theory, for instance, it is common to approximate measurable functions by indicator functions or simple functions. But in other parts of analysis, it is often more convenient to approximate rough functions by continuous or smooth functions (perhaps with compact support, or some other decay condition), or by functions in some algebraic class, such as the class of polynomials or trigonometric polynomials.
In order to approximate rough functions by more continuous ones, one of course needs tools that can generate continuous functions with some specified behaviour. The two basic tools for this are Urysohn’s lemma, which approximates indicator functions by continuous functions, and the Tietze extension theorem, which extends continuous functions on a subdomain to continuous functions on a larger domain. An important consequence of these theorems is the Riesz representation theorem for linear functionals on the space of compactly supported continuous functions, which describes such functionals in terms of Radon measures.
Sometimes, approximation by continuous functions is not enough; one must approximate continuous functions in turn by an even smoother class of functions. A useful tool in this regard is the Stone-Weierstrass theorem, that generalises the classical Weierstrass approximation theorem to more general algebras of functions.
As an application of this theory (and of many of the results accumulated in previous lecture notes), we will present (in an optional section) the commutative Gelfand-Neimark theorem classifying all commutative unital -algebras.
— 1. Urysohn’s lemma —
Let be a topological space. An indicator function
in this space will not typically be a continuous function (indeed, if
is connected, this only happens when
is the empty set or the whole set). Nevertheless, for certain topological spaces, it is possible to approximate an indicator function by a continuous function, as follows.
Lemma 1 (Urysohn’s lemma) Let
be a topological space. Then the following are equivalent:
- (i) Every pair of disjoint closed sets
in
can be separated by disjoint open neighbourhoods
,
.
- (ii) For every closed set
in
and every open neighbourhood
of
, there exists an open set
and a closed set
such that
.
- (iii) For every pair of disjoint closed sets
in
, there exists a continuous function
which equals
on
and
on
.
- (iv) For every closed set
in
and every open neighbourhood
of
, there exists a continuous function
such that
for all
.
A topological space which obeys any (and hence all) of (i-iv) is known as a normal space; definition (i) is traditionally taken to be the standard definition of normality. We will give some examples of normal spaces shortly.
Proof: The equivalence of (iii) and (iv) is clear, as the complement of a closed set is an open set and vice versa. The equivalence of (i) and (ii) follows similarly.
To deduce (i) from (iii), let be disjoint closed sets, let
be as in (iii), and let
be the open sets
and
.
The only remaining task is to deduce (iv) from (ii). Suppose we have a closed set and an open set
with
. Applying (ii), we can find an open set
and a closed set
such that
Applying (ii) two more times, we can find more open sets and closed sets
such that
Iterating this process, we can construct open sets and closed sets
for every dyadic rational
in
such that
for all
, and
for any
.
If we now define , where
ranges over dyadic rationals between
and
, and with the convention that the empty set has sup
and inf
, one easily verifies that the sets
and
are open for every real number
, and so
is continuous as required.
The definition of normality is very similar to the Hausdorff property, which separates pairs of points instead of closed sets. Indeed, if every point in is closed (a property known as the
property), then normality clearly implies the Hausdorff property. The converse is not always true, but (as the term suggests) in practice most topological spaces one works with in real analysis are normal. For instance:
Exercise 1 Show that every metric space is normal.
Exercise 2 Let
be a Hausdorff space.
- Show that a compact subset of
and a point disjoint from that set can always be separated by open neighbourhoods.
- Show that a pair of disjoint compact subsets of
can always be separated by open neighbourhoods.
- Show that every compact Hausdorff space is normal.
Exercise 3 Let
be the real line with the usual topology
, and let
be the topology on
generated by
and the set
consisting only of the rationals
; in other words,
is the coarsest refinement of the usual topology that makes the set of rationals
an open set. Show that
is Hausdorff, with every point closed, but is not normal.
The above example was a simple but somewhat artificial example of a non-normal space. One can create more “natural” examples of non-normal Hausdorff spaces (with every point closed), but establishing non-normality becomes more difficult. The following example is due to Stone.
Exercise 4 Let
be the space of natural number-valued tuples
, endowed with the product topology (i.e. the topology of pointwise convergence).
- Show that
is Hausdorff, and every point is closed.
- For
, let
be the set of all tuples
such that
for all
outside of a countable set, and such that
is injective on this finite set (i.e. there do not exist distinct
such that
). Show that
are disjoint and closed.
- Show that given any open neighbourhood
of
, there exists disjoint finite subsets
of
and an injective function
such that for any
, any
such that
for all
and is identically
on
, lies in
.
- Show that any open neighbourhood of
and any open neighbourhood of
necessarily intersect, and so
is not normal.
- Conclude that
with the product topology is not normal.
The property of being normal is a topological one, thus if one topological space is normal, then any other topological space homeomorphic to it is also normal. However, (unlike, say, the Hausdorff property), the property of being normal is not preserved under passage to subspaces:
Exercise 5 Given an example of a subspace of a normal space which is not normal. (Hint: use Exercise 4, possibly after replacing
with a homeomorphic equivalent.)
Let be the space of real continuous compactly supported functions on
. Urysohn’s lemma generates a large number of useful elements of
, in the case when
is locally compact Hausdorff:
Exercise 6 Let
be a locally compact Hausdorff space, let
be a compact set, and let
be an open neighbourhood of
. Show that there exists
such that
for all
. (Hint: First use the local compactness of
to find a neighbourhood of
with compact closure; then restrict
to this neighbourhood. The closure of
is now a compact set; restrict everything to this set, at which point the space becomes normal.)
One consequence of this exercise is that tends to be dense in many other function spaces. We give an important example here:
Definition 2 (Radon measure) Let
be a locally compact Hausdorff space that is also
-compact, and let
be the Borel
-algebra. An (unsigned) Radon measure is a unsigned measure
with the following properties:
- (Local finiteness) For any compact subset
of
,
is finite.
- (Outer regularity) For any Borel set
of
,
.
- (Inner regularity) For any Borel set
of
,
.
Example 1 Lebesgue measure
on
is a Radon measure, as is any absolutely continuous unsigned measure
, where
. More generally, if
is Radon and
is a finite unsigned measure which is absolutely continuous with respect to
, then
is Radon. On the other hand, counting measure on
is not Radon (it is not locally finite). It is possible to define Radon measures on Hausdorff spaces that are not
-compact or locally compact, but the theory is more subtle and will not be considered here. We will study Radon measures more thoroughly in the next section.
Proposition 3 Let
be a locally compact Hausdorff space that is also
-compact, and let
be a Radon measure on
. Then for any
,
is a dense subset in (real-valued)
. In other words, every element of
can be expressed as a limit (in
) of continuous functions of compact support.
Proof: Since continuous functions of compact support are bounded, and compact sets have finite measure, we see that is a subspace of
. We need to show that the closure
of this space contains all of
.
Let be a Borel set of finite measure. Applying inner and outer regularity, we can find a sequence of compact sets
and open sets
such that
. Applying Exercise 6, we can then find
such that
. In particular, this implies (by the squeeze theorem) that
converges in
to
(here we use the finiteness of
); thus
lies in
for any measurable set
. By linearity, all simple functions lie in
; taking closures, we see that any
function lies in
, as desired.
Of course, the real-valued version of the above proposition immediately implies a complex-valued analogue. On the other hand, the claim fails when :
Exercise 7 Let
be a locally compact Hausdorff space that is
-compact, and let
be a Radon measure. Show that the closure of
in
is
, the space of continuous real-valued functions which vanish at infinity (i.e. for every
there exists a compact set
such that
for all
). Thus, in general,
is not dense in
.
Thus we see that the norm is strong enough to preserve continuity in the limit, whereas the
norms are (locally) weaker and permit discontinuous functions to be approximated by continuous ones.
Another important consequence of Urysohn’s lemma is the Tietze extension theorem:
Theorem 4 (Tietze extension theorem) Let
be a normal topological space, let
be a bounded interval, let
be a closed subset of
, and let
be a continuous function. Then there exists a continuous function
which extends
, i.e.
for all
.
Proof: It suffices to find an continuous extension taking values in the real line rather than in
, since one can then replace
by
(note that min and max are continuous operations).
Let be the restriction map
. This is clearly a continuous linear map; our task is to show that it is surjective, i.e. to find a solution to the equation
for each
. We do this by the standard analysis trick of getting an approximate solution to
first, and then using iteration to boost the approximate solution to an exact solution.
Let have sup norm
, thus
takes values in
. To solve the problem
, we approximate
by
. By Urysohn’s lemma, we can find a continuous function
such that
on the closed set
and
on the closed set
. Now,
is not quite equal to
; but observe from construction that
has sup norm
.
Scaling this fact, we conclude that, given any , we can find a decomposition
, where
and
.
Starting with any , we can now iterate this construction to express
for all
, where
and
. As
is a Banach space, we see that
converges absolutely to some limit
, and that
, as desired.
Remark 1 Observe that Urysohn’s lemma can be viewed the special case of the Tietze extension theorem when
is the union of two disjoint closed sets, and
is equal to
on one of these sets and equal to
on the other.
Remark 2 One can extend the Tietze extension theorem to finite-dimensional vector spaces: if
is a closed subset of a normal vector space
and
is bounded and continuous, then one has a bounded continuous extension
. Indeed, one simply applies the Tietze extension theorem to each component of
separately. However, if the range space is replaced by a space with a non-trivial topology, then there can be topological obstructions to continuous extension. For instance, a map
from a two-point set into a topological space
is always continuous, but can be extended to a continuous map
if and only if
and
lie in the same path-connected component of
. Similarly, if
is a map from the unit circle into a topological space
, then a continuous extension from
to
exists if and only if the closed curve
is contractible to a point in
. These sorts of questions require the machinery of algebraic topology to answer them properly, and are beyond the scope of this course.
There are analogues for the Tietze extension theorem in some other categories of functions. For instance, in the Lipschitz category, we have
Exercise 8 Let
be a metric space, let
be a subset of
, and let
be a Lipschitz continuous map with some Lipschitz constant
(thus
for all
). Show that there exists an extension
of
which is Lipschitz continuous with the same Lipschitz constant
. (Hint: A “greedy” algorithm will work here: pick
to be as large as one can get away with (or as small as one can get away with.))
One can also remove the requirement that the function be bounded in the Tietze extension theorem:
Exercise 9 Let
be a normal topological space, let
be a closed subset of
, and let
be a continuous map (not necessarily bounded). Then there exists an extension
of
which is still continuous. (Hint: first “compress”
to be bounded by working with, say,
(other choices are possible), and apply the usual Tietze extension theorem. There will be some sets in which one cannot invert the compression function, but one can deal with this by a further appeal to Urysohn’s lemma to damp the extension out on such sets.)
There is also a locally compact Hausdorff version of the Tietze extension theorem:
Exercise 10 Let
be locally compact Hausdorff, let
be compact, and let
. Then there exists
which extends
.
Proposition 3 shows that measurable functions in can be approximated by continuous functions of compact support (cf. Littlewood’s second principle). Another approximation result in a similar spirit is Lusin’s theorem:
Theorem 5 (Lusin’s theorem) Let
be a locally compact Hausdorff space that is
-compact, and let
be a Radon measure. Let
be a measurable function supported on a set of finite measure, and let
. Then there exists
which agrees with
outside of a set of measure at most
.
Proof: Observe that as is finite everywhere, it is bounded outside of a set of arbitrarily small measure. Thus we may assume without loss of generality that
is bounded. Similarly, as
is
-compact (or by inner regularity), the support of
differs from a compact set by a set of arbitrarily small measure; so we may assume that
is also supported on a compact set
. By Exercise 10, it then suffices to show that
is continuous on the complement of an open set of arbitrarily small measure; by outer regularity, we may delete the adjective “open” from the preceding sentence.
As is bounded and compactly supported,
lies in
for every
, and using Proposition 3 and Chebyshev’s inequality, it is not hard to find, for each
, a function
which differs from
by at most
outside of a set of measure at most
(say). In particular,
converges uniformly to
outside of a set of measure at most
, and
is therefore continuous outside this set. The claim follows.
Another very useful application of Urysohn’s lemma is to create partitions of unity.
Lemma 6 (Partitions of unity) Let
be a normal topological space, and let
be a collection of closed sets that cover
. For each
, let
be an open neighbourhood of
, which are finitely overlapping in the sense that each
has a neighbourhood that intersects at most finitely many of the
. Then there exists a continuous function
supported on
for each
such that
for all
.
If
is locally compact Hausdorff instead of normal, and the
are compact, then one can take the
to be compactly supported.
Proof: Suppose first that is normal. By Urysohn’s lemma, one can find a continuous function
for each
which is supported on
and equals
on the closed set
. Observe that the function
is well-defined, continuous and bounded below by
. The claim then follows by setting
.
The final claim follows by using Exercise 6 instead of Urysohn’s lemma.
Exercise 11 Let
be a topological space. A function
is said to be upper semi-continuous if
is open for all real
, and lower semi-continuous if
is open for all real
.
- Show that an indicator function
is upper semi-continuous if and only if
is closed, and lower semi-continuous if and only if
is open.
- If
is normal and Hausdorff, show that a function
is upper semi-continuous if and only if
for all
, and lower semi-continuous if and only if
for all
, where we write
if
for all
.
— 2. The Riesz representation theorem —
Let be a locally compact Hausdorff space which is also
-compact. In Definition 2 we defined the notion of a Radon measure. Such measures are quite common in real analysis. For instance, we have the following result.
Theorem 7 Let
be a non-negative finite Borel measure on a compact metric space
. Then
is a Radon measure.
Proof: As is finite, it is locally finite, so it suffices to show inner and outer regularity. Let
be the collection of all Borel subsets
of
such that
It will then suffice to show that every Borel set lies in (note that as
is compact, a subset
of
is closed if and only if it is compact).
Clearly contains the empty set and the whole set
, and is closed under complements. It is also closed under finite unions and intersections. Indeed, given two sets
, we can find a sequences
,
of closed sets
and open sets
such that
and
. Since
we have (by monotonicity of ) that
and similarly
and so .
One can also show that is closed under countable disjoint unions and is thus a
-algebra. Indeed, given disjoint sets
and
, pick a closed
and open
such that
; then
and
for any , and the claim follows from the squeeze test.
To finish the claim it suffices to show that every open set lies in
. For this it will suffice to show that
is a countable union of closed sets. But as
is a compact metric space, it is separable (Lemma 4 from Notes 10), and so
has a countable dense subset
. One then easily verifies that every point in the open set
is contained in a closed ball of rational radius centred at one of the
that is in turn contained in
; thus
is the countable union of closed sets as desired.
This result can be extended to more general spaces than compact metric spaces, for instance to Polish spaces (provided that the measure remains finite). For instance:
Exercise 12 Let
be a locally compact metric space which is
-compact, and let
be an unsigned Borel measure which is finite on every compact set. Show that
is a Radon measure.
When the assumptions of are weakened, then it is possible to find locally finite Borel measures that are not Radon measures, but they are somewhat pathological in nature.
Exercise 13 Let
be a locally compact Hausdorff space which is
-compact, and let
be a Radon measure. Define a
set to be a countable union of closed sets, and a
set to be a countable intersection of open sets. Show that every Borel set can be expressed as the union of an
set and a null set, and as a
set with a null subset removed.
If is a Radon measure on
, then we can define the integral
for every
, since
assigns every compact set a finite measure. Furthermore,
is a linear functional on
which is positive in the sense that
whenever
is non-negative. If we place the uniform norm on
, then
is continuous if and only if
is finite; but we will not use continuity for now, relying instead on positivity.
The fundamentally important Riesz representation theorem for such spaces asserts that this is the only way to generate such linear functionals:
Theorem 8 (Riesz representation theorem for
, unsigned version) Let
be a locally compact Hausdorff space which is also
-compact. Let
be a positive linear functional. Then there exists a unique Radon measure
on
such that
.
Remark 3 The
-compactness hypothesis can be dropped (after relaxing the inner regularity condition to only apply to open sets, rather than to all sets); but I will restrict attention here to the
-compact case (which already covers a large fraction of the applications of this theorem) as the argument simplifies slightly.
Proof: We first prove the uniqueness, which is quite easy due to all the properties that Radon measures enjoy. Suppose we had two Radon measures such that
; in particular, we have
for all . Now let
be a compact set, and let
be an open neighbourhood of
. By Exercise 6, we can find
with
; applying this to (1), we conclude that
Taking suprema in and using inner regularity, we conclude that
; exchanging
and
we conclude that
and
agree on open sets; by outer regularity we then conclude that
and
agree on all Borel sets.
Now we prove existence, which is significantly trickier. We will initially make the simplifying assumption that is compact (so in particular
), and remove this assumption at the end of the proof.
Observe that is monotone on
, thus
whenever
.
We would like to define the measure on Borel sets
by defining
. This does not work directly, because
is not continuous. To get around this problem we shall begin by extending the functional
to the class
of bounded lower semi-continuous non-negative functions. We define
for such functions by the formula
(cf. Exercise 11). This definition agrees with the existing definition of in the case when
is continuous. Since
is finite and
is monotone, one sees that
is finite (and non-negative) for all
. One also easily sees that
is monotone on
:
whenever
and
, and homogeneous in the sense that
for all
and
. It is also easy to verify the super-additivity property
for
; this simply reflects the linearity of
on
, together with the fact that if
and
, then
.
We now complement the super-additivity property with a countably sub-additive one: if is a sequence, and
is such that
for all
, then
.
Pick a small . It will suffice to show that
(say) whenever
is such that
, and
denotes a quantity bounded in magnitude by
, where
is a quantity that is independent of
.
Fix . For every
, we can find a neighbourhood
of
such that
for all
; we can also find
such that
. By shrinking
if necessary, we see from the lower semicontinuity of the
and
that we can also ensure that
for all
and
.
By normality, we can find open neighbourhoods of
whose closure lies in
. The
form an open cover of
. Since we are assuming
to be compact, we can thus find a finite subcover
of
. Applying Lemma 6, we can thus find a partition of unity
, where each
is supported on
.
Let be such that
. Then we can write
. If
is in this sum, then
, and thus (for
small enough)
, and hence
. We can then write
and thus
(here we use the fact that and that the continuous compactly supported function
is bounded). Observe that only finitely many summands are non-zero. We conclude that
(here we use that and so
is finite). On the other hand, for any
and any
, the expression
is bounded from above by
since and
, this is bounded above in turn by
We conclude that
and the sub-additivity claim follows.
Combining sub-additivity and super-additivity we see that is additive:
for
.
Now that we are able to integrate lower semi-continuous functions, we can start defining the Radon measure . When
is open, we define
by
which is well-defined and non-negative since is bounded, non-negative and lower semi-continuous. When
is closed we define
by complementation:
this is compatible with the definition of on open sets by additivity of
, and is also non-negative. The monotonicity of
implies monotonicity of
: in particular, if a closed set
lies in an open set
, then
.
Given any set , define the outer measure
and the inner measure
thus . We call a set
measurable if
. By arguing as in the proof of Theorem 7, we see that the class of measurable sets is a Boolean algebra. Next, we claim that every open set
is measurable. Indeed, unwrapping all the definitions we see that
Each in this supremum is supported in some closed subset
of
, and from this one easily verifies that
. Similarly, every closed set
is measurable. We can now extend
to measurable sets by declaring
when
is measurable; this is compatible with the previous definitions of
.
Next, let be a countable sequence of disjoint measurable sets. Then for any
, we can find open neighbourhoods
of
and closed sets
in
such that
and
. Using the sub-additivity of
on
, we have
. Similarly, from the additivity of
we have
. Letting
, we conclude that
is measurable with
. Thus the Boolean algebra of measurable sets is in fact a
-algebra, and
is a countably additive measure on it. From construction we also see that it is finite, outer regular, and inner regular, and therefore is a Radon measure. The only remaining thing to check is that
for all
. If
is a finite non-negative linear combination of indicator functions of open sets, the claim is clear from the construction of
and the additivity of
on
; taking uniform limits, we obtain the claim for non-negative continuous functions, and then by linearity we obtain it for all functions.
This concludes the proof in the case when is compact. Now suppose that
is
-compact. Then we can find a partition of unity
into continuous compactly supported functions
, with each
being contained in the support of finitely many
. (Indeed, from
-compactness and the locally compact Hausdorff property one can find a nested sequence
of compact sets, with each
in the interior of
, such that
. Using Exercise 6, one can find functions
that equal
on
and are supported on
; now take
and
.) Observe that
for all
. From the compact case we see that there exists a finite Radon measure
such that
for all
; setting
one can verify (using the monotone convergence theorem) that
obeys the required properties.
Remark 4 One can also construct the Radon measure
using the Carátheodory extension theorem; this proof of the Riesz representation theorem can be found in many real analysis texts. A third method is to first create the space
by taking the completion of
with respect to the
norm
, and then define
. It seems to me that all three proofs are about equally lengthy, and ultimately rely on the same ingredients; they all seem to have their strengths and weaknesses, and involve at least one tricky computation somewhere (in the above argument, the most tricky thing is the countable subadditivity of
on lower semicontinuous functions). I have yet to find a proof of this theorem which is both clean and conceptual, and would be happy to learn of other proofs of this theorem.
Remark 5 One can use the Riesz representation theorem to provide an alternate construction of Lebesgue measure, say on
. Indeed, the Riemann integral already provides a positive linear functional on
, which by the Riesz representation theorem must come from a Radon measure, which can be easily verified to assign the value
to every interval
and thus must agree with Lebesgue measure. The same approach lets one define volume measures on manifolds with a volume form.
Exercise 14 Let
be a locally compact Hausdorff space which is
-compact, and let
be a Radon measure. For any non-negative Borel measurable function
, show that
and
Similarly, for any non-negative lower semi-continuous function
, show that
Now we consider signed functionals on , which we now turn into a normed vector space using the uniform norm. The key lemma here is the following variant of the Jordan decomposition theorem.
Lemma 9 (Jordan decomposition for functions) Let
be a (real) continuous linear functional. Then there exist positive linear functions
such that
.
Proof: For , we define
Clearly for
; one also easily verifies the homogeneity property
and super-additivity property
for
and
. On the other hand, if
are such that
, then we can decompose
for some
with
and
; for instance we can take
and
. From this we can complement super-additivity with sub-additivity and conclude that
.
Every function in can be expressed as the difference of two functions in
. From the additivity and homogeneity of
on
we may thus extend
uniquely to be a linear functional on
. Since
is bounded on
, we see that
is also. If we then define
, one quickly verifies all the required properties.
Exercise 15 Show that among all possible choices for the functionals
appearing in the above lemma, there is a unique choice which is minimal in the sense that for any other functionals
obeying the conclusions of the lemma, one has
and
for all nonnegative
.
Define a signed Radon measure on a -compact, locally compact Hausdorff space
to be a signed Borel measure
whose positive and negative variations are both Radon. It is easy to see that a signed Radon measure
generates a linear functional
on
as before, and
is continuous if
is finite. We have a converse:
Exercise 16 (Riesz representation theorem, signed version) Let
be a locally compact Hausdorff space which is also
-compact, and let
be a continuous linear functional. Then there exists a unique signed finite Radon measure
such that
. (Hint: combine Theorem 8 with Lemma 9.)
The space of signed finite Radon measures on is denoted
, or
for short.
Exercise 17 Show that the space
, with the total variation norm
, is a real Banach space, which is isomorphic to the dual of both
and its completion
, thus
Remark 6 Note that the previous exercise generalises the identifications
from previous notes. For compact Hausdorff spaces
, we have
, and thus
. For locally compact Hausdorff spaces that are
-compact but not compact, we instead have
, where
is the Stone-Cech compactification of
, which we will discuss in later notes.
Remark 7 One can of course also define complex Radon measures to be those complex finite Borel measures whose real and imaginary parts are signed Radon measures, and define
to be the space of all such measures; then one has analogues of the above identifications. We omit the details.
Exercise 18 Let
be two locally compact Hausdorff spaces that are also
-compact, and let
be a continuous map. If
is an unsigned finite Radon measure on
, show that the pushforward measure
on
, defined by
, is a Radon measure on
. What happens for infinite measures? Establish the same fact for signed finite Radon measures.
Let be locally compact Hausdorff and
-compact. As
is equivalent to the dual of the Banach space
, it acquires a weak* topology (see Notes 11), known as the vague topology. A sequence of Radon measures
then converges vaguely to a limit
if and only if
for all
.
Exercise 19 Let
be Lebesgue measure on the real line (with the usual topology).
- Show that the measures
converge vaguely as
to the Dirac mass
at the origin
.
- Show that the measures
converge vaguely as
to the measure
. (Hint: Continuous, compactly supported functions are Riemann integrable.)
- Show that the measures
converge vaguely as
to the zero measure
.
Exercise 20 Let
be locally compact Hausdorff and
-compact. Show that for every unsigned Radon measure
, the map
defined by sending
to the measure
is an isometry, thus
can be identified with a subspace of
. Show that this subspace is closed in the norm topology, but give an example to show that it need not be closed in the vague topology. Show that
, where
ranges over all unsigned Radon measures on
; thus one can think of
as many
‘s “glued together”.
Exercise 21 Let
be a locally compact Hausdorff space which is
-compact. Let
be a sequence of functions, and let
be another function. Show that
converges weakly to
in
if and only if the
are uniformly bounded and converge pointwise to
.
Exercise 22 Let
be a locally compact metric space which is
-compact.
- Show that the space of finitely supported measures in
is a dense subset of
in the vague topology.
- Show that a Radon probability measure in
can be expressed as the vague limit of a sequence of discrete (i.e. finitely supported) probability measures.
— 3. The Stone-Weierstrass theorem —
We have already seen how rough functions (e.g. functions) can be approximated by continuous functions. Now we study in turn how continuous functions can be approximated by even more special functions, such as polynomials. The natural topology to work with here is the uniform topology (since uniform limits of continuous functions are continuous).
For non-compact spaces, such as , it is usually not possible to approximate continuous functions uniformly by a smaller class of functions. For instance, the function
cannot be approximated uniformly by polynomials on
, since
is bounded, the only bounded polynomials are the constants, and constants cannot converge to anything other than another constant. On the other hand, on a compact domain such as
, one can easily approximate
uniformly by polynomials, for instance by using Taylor series. So we will focus instead on compact Hausdorff spaces
such as
, in which continuous functions are automatically bounded.
The space of (real-valued) polynomials is a subspace of the Banach space
. But it is also closed under pointwise multiplication
, making
an algebra, and not merely a vector space. We can then rephrase the classical Weierstrass approximation theorem as the assertion that
is dense in
.
One can then ask the more general question of when a sub-algebra of
– i.e. a subspace closed under pointwise multiplication – is dense. Not every sub-algebra is dense: the algebra of constants, for instance, will not be dense in
when
has at least two points. Another example in a similar spirit: given two distinct points
in
, the space
is a sub-algebra of
, but it is not dense, because it is already closed, and cannot separate
and
in the sense that it cannot produce a function that assigns different values to
and
.
The remarkable Stone-Weierstrass theorem shows that this inability to separate points is the only obstruction to density, at least for algebras with the identity.
Theorem 10 (Stone-Weierstrass theorem, real version) Let
be a compact Hausdorff space, and let
be a sub-algebra of
which contains the constant function
and separates points (i.e. for every distinct
, there exists at least one
in
such that
. Then
is dense in
.
Remark 8 Observe that this theorem contains the Weierstrass approximation theorem as a special case, since the algebra of polynomials clearly separates points. Indeed, we will use (a very special case) of the Weierstrass approximation theorem in the proof.
Proof: It suffices to verify the claim for algebras which are closed in the
topology, since the claim follows in the general case by replacing
with its closure (note that the closure of an algebra is still an algebra).
Observe from the Weierstrass approximation theorem that on any bounded interval , the function
can be expressed as the uniform limit of polynomials
; one can even write down explicit formulae for such a
, though we will not need such formulae here. Since continuous functions on the compact space
are bounded, this implies that for any
, the function
is the uniform limit of polynomial combinations
of
. As
is an algebra, the
lie in
; as
is closed; we see that
lies in
.
Using the identities ,
, we conclude that
is a lattice in the sense that one has
whenever
.
Now let and
. We would like to find
such that
for all
.
Given any two points , we can at least find a function
such that
and
; this follows since the vector space
separates points and also contains the identity function (the case
needs to be treated separately). We now use these functions
to build the approximant
. First, observe from continuity that for every
there exists an open neighbourhood
of
such that
for all
. By compactness, for any fixed
we can cover
by a finite number of these
. Taking the max of all the
associated to this finite subcover, we create another function
such that
and
for all
. By continuity, we can find an open neighbourhood
of
such that
for all
. Again applying compactness, we can cover
by a finite number of the
; taking the min of all the
associated to this finite subcover we obtain
with
for all
, and the claim follows.
There is an analogue of the Stone-Weierstrass theorem for algebras that do not contain the identity:
Exercise 23 Let
be a compact Hausdorff space, and let
be a closed sub-algebra of
which separates points but does not contain the identity. Show that there exists a unique
such that
.
The Stone-Weierstrass theorem is not true as stated in the complex case. For instance, the space of complex-valued functions on the closed unit disk
has a closed proper sub-algebra that separates points, namely the algebra
of functions in
that are holomorphic on the interior of this disk. Indeed, by Cauchy’s theorem and its converse (Morera’s theorem), a function
lies in
if and only if
for every closed contour
in
, and one easily verifies that this implies that
is closed; meanwhile, the holomorphic function
separates all points. However, the Stone-Weierstrass theorem can be recovered in the complex case by adding one further axiom, namely that the algebra be closed under conjugation:
Exercise 24 (Stone-Weierstrass theorem, complex version) Let
be a compact Hausdorff space, and let
be a complex sub-algebra of
which contains the constant function
, separates points, and is closed under the conjugation operation
. Then
is dense in
.
Exercise 25 Let
be the space of trigonometric polynomials
on the unit circle
, where
and the
are complex numbers. Show that
is dense in
(with the uniform topology), and that
is dense in
(with the
topology) for all
.
Exercise 26 Let
be a locally compact Hausdorff space that is
-compact, and let
be a sub-algebra of
which separates points and contains the identity function. Show that for every function
there exists a sequence
which converges to
uniformly on compact subsets of
.
Exercise 27 Let
be compact Hausdorff spaces. Show that every function
can be expressed as the uniform limit of functions of the form
, where
and
.
Exercise 28 Let
be a family of compact Hausdorff spaces, and let
be the product space (with the product topology). Let
. Show that
can be expressed as the uniform limit of continuous functions
, each of which only depend on finitely many of the coordinates in
, thus there exists a finite subset
of
and a continuous function
such that
for all
.
One useful application of the Stone-Weierstrass theorem is to demonstrate separability of spaces such as .
Proposition 11 Let
be a compact metric space. Then
and
are separable.
Proof: It suffices to show that is separable. By Lemma 4 of Notes 10,
has a countable dense subset
. By Urysohn’s lemma, for each
we can find a function
which equals
on
and is supported on
. The
can then easily be verified to separate points, and so by the Stone-Weierstrass theorem, the algebra of polynomial combinations of the
in
are dense; this implies that the algebra of rational polynomial combinations of the
are dense, and the claim follows.
Combining this with the Riesz representation theorem and the sequential Banach-Alaoglu theorem, we obtain
Corollary 12 If
is a compact metric space, then the closed unit ball of
is sequentially compact in the vague topology.
Combining this with Theorem 7, we conclude a special case of Prokhorov’s theorem:
Corollary 13 (Prokhorov’s theorem, compact case) Let
be a compact metric space, and let
be a sequence of Borel (hence Radon) probability measures on
. Then there exists a subsequence of
which converge vaguely to another Borel probability measure
.
Exercise 29 (Prokhorov’s theorem, non-compact case) Let
be a locally compact metric space which is
-compact, and let
be a sequence of Borel probability measures. We assume that the sequence
is tight, which means that for every
there exists a compact set
such that
for all
. Show that there is a subsequence of
which converges vaguely to another Borel probability measure
. If tightness is not assumed, show that there is a subsequence which converges vaguely to a non-negative Borel measure
, but give an example to show that this measure need not be a probability measure.
This theorem can be used to establish Helly’s selection theorem:
Exercise 30 (Helly’s selection theorem) Let
be a sequence of functions whose total variation is uniformly bounded in
, and which is bounded at one point
(i.e.
is bounded). Show that there exists a subsequence of
which converges pointwise almost everywhere on compact subsets of
. (Hint: one can deduce this from Prokhorov’s theorem using the fundamental theorem of calculus for functions of bounded variation.)
— 4. The commutative Gelfand-Naimark theorem (optional) —
One particularly beautiful application of the machinery developed in the last few notes is the commutative Gelfand-Naimark theorem, that classifies commutative -algebras, and is of importance in spectral theory, operator algebras, and quantum mechanics.
Definition 14 A complex Banach algebra is a complex Banach space
which is also a complex algebra, such that
for all
. An algebra is unital if it contains a multiplicative identity
, and commutative if
for all
. A
-algebra is a complex Banach algebra with an anti-homomorphism map
from
to
(thus
,
, and
for
and
) which is an isometry (thus
for all
), an involution (thus
for all
), and obeys the
identity
for all
.
A homomorphism
between two
-algebras is a continuous algebra homomorphism such that
for all
. An isomorphism is an homomorphism whose inverse exists and is also a homomorphism; two
-algebras are isomorphic if there exists an isomorphism between them.
Exercise 31 If
is a Hilbert space, and
is the algebra of bounded linear operators on this space, with the adjoint map
and the operator norm, show that
is a unital
-algebra (not necessarily commutative). Indeed, one can think of
-algebras as an abstraction of a space of bounded linear operators on a Hilbert space (this is basically the content of the non-commutative Gelfand-Naimark theorem, which we will not discuss here).
Exercise 32 If
is a compact Hausdorff space, show that
is a unital commutative
-algebra, with involution
.
The remarkable (unital commutative) Gelfand-Naimark theorem asserts the converse statement to Exercise 32:
Theorem 15 (Unital commutative Gelfand-Naimark theorem) Every unital commutative
-algebra
is isomorphic to
for some compact Hausdorff space
.
There are analogues of this theorem for non-unital or non-commutative -algebras, but for simplicity we shall restrict attention to the unital commutative case. We first need some spectral theory.
Exercise 33 Let
be a unital Banach algebra. Show that if
is such that
, then
is invertible. (Hint: use Neumann series.) Conclude that the space
of invertible elements of
is open.
Define the spectrum of an element
to be the set of all
such that
is not invertible.
Exercise 34 If
is a unital Banach algebra and
, show that
is a compact subset of
that is contained inside the disk
.
Exercise 35 (Beurling-Gelfand spectral radius formula) If
is a unital Banach algebra and
, show that
is non-empty with
. (Hint: To get the upper bound, observe that if
is invertible for some
, then so is
, then use Exercise 34. To get the lower bound, first observe that for any
, the function
is holomorphic on the complement of
, which is already enough (with Liouville’s theorem) to show that
is non-empty. Let
be arbitrary, then use Laurent series to show that
for all
and some
independent of
. Then divide by
and use the uniform boundedness principle to conclude.)
Exercise 36 (
-algebra spectral radius formula) Let
be a unital
-algebra. Show that
for all
and
. Conclude that any homomorphism between
-algebras has operator norm at most
. Also conclude that
when
is self-adjoint.
The next important concept is that of a character.
Definition 16 Let
be a unital commutative
-algebra. A character of
is be an element
in the dual Banach space such that
,
, and
for all
; equivalently, a character is a homomorphism from
to
(viewed as a (unital)
algebra). We let
be the space of all characters; this space is known as the spectrum of
.
Exercise 37 If
is a unital commutative
-algebra, show that
is a compact Hausdorff subset of
in the weak-* topology. (Hint: first use the spectral radius formula to show that all characters have operator norm
, then use the Banach-Alaoglu theorem.)
Exercise 38 Define an ideal of a unital commutative
-algebra
to be a proper subspace
of
such that
for all
and
. Show that if
, then the kernel
is a maximal ideal in
; conversely, if
is a maximal ideal in
, show that
is closed, and there is exactly one
such that
. Thus the spectrum of
can be canonically identified with the space of maximal ideals in
.
Exercise 39 Let
be a compact Hausdorff space, and let
be the
-algebra
. Show that for each
, the operation
is a character of
. Show that the map
is a homeomorphism from
to
; thus the spectrum of
can be canonically identified with
. (Hint: use Exercise 23 to show the surjectivity of
, Urysohn’s lemma to show injectivity, and Corollary 2 of Notes 10 to show the homeomorphism property.)
Inspired by the above exercise, we define the Gelfand representation , by the formula
.
Exercise 40 Show that if
is a unital commutative
-algebra, then the Gelfand representation is a homomorphism of
-algebras.
Exercise 41 Let
be a non-invertible element of a unital commutative
-algebra
. Show that
vanishes at some
. (Hint: the set
is a proper ideal of
, and thus by Zorn’s lemma is contained in a maximal ideal.)
Exercise 42 Show that if
is a unital commutative
-algebra, then the Gelfand representation is an isometry. (Hint: use Exercise 36 and Exercise 41.)
Exercise 43 Use the complex Stone-Weierstrass theorem and Exercises 40, 42 to conclude the proof of Theorem 15.

91 comments
Comments feed for this article
1 January, 2015 at 8:08 am
Alex
In Lemma 9, you don’t really need to equip with a topology in order to show that every linear functional
with a topology in order to show that every linear functional 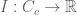 can be written as a difference of two positive functionals
can be written as a difference of two positive functionals  and
and  . If
. If  is equipped with the uniform norm then
is equipped with the uniform norm then 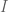 is continuous if and only if the corresponding Radon measure is a finite signed measure. However, we can also equip
is continuous if and only if the corresponding Radon measure is a finite signed measure. However, we can also equip  with a locally convex topology (see http://en.wikipedia.org/wiki/Radon_measure#Measures). In this case, we have more continuous functionals, namely signed Radon measures that can be also infinite on one side or even “real” Radon measures, i.e. differences of positive Radon measures, that cannot be written in terms of a set function.
with a locally convex topology (see http://en.wikipedia.org/wiki/Radon_measure#Measures). In this case, we have more continuous functionals, namely signed Radon measures that can be also infinite on one side or even “real” Radon measures, i.e. differences of positive Radon measures, that cannot be written in terms of a set function.
23 April, 2015 at 5:22 am
Bob
Dear Prof. Tao,
can you give me a reference about the proof of Riesz representation theorem via creating L^1 as the completion of C_c(X)?
Thanks
24 April, 2015 at 9:21 pm
eshetu
Could anyone help me the proof of theorem 15? Thanks.
12 October, 2015 at 12:35 pm
275A, Notes 2: Product measures and independence | What's new
[…] for any compact separable metric spaces. Radon measures are often used in real analysis (see e.g. these lecture notes) but we will not develop their theory further […]
2 November, 2015 at 7:06 pm
275A, Notes 4: The central limit theorem | What's new
[…] distribution (this is a consequence of the Riesz representation theorem, discussed for instance in this blog post). As a consequence of the insensitivity of convergence in distribution to equivalence in […]
13 November, 2015 at 9:06 am
Anonymous
The formulation of partitions of unity looks quite different from the ones from the Wikipedia link you gave.
What is essential with using the “closed” cover in Lemma 6? Can one formulate it by using only “open” cover?
I’ve seen the smooth partitions of unity in PDE (for example in Evans’s book) which says that if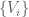 is an open cover of an open subset
is an open cover of an open subset  of
of 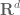 , then there exists
, then there exists ![\zeta_i:U\to[0,1]](https://s0.wp.com/latex.php?latex=%5Czeta_i%3AU%5Cto%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) such that
such that  and the sum of
and the sum of  equals to
equals to  pointwise on $U$. Can this be deduced from Lemma 6 (and suitable mollification)?
pointwise on $U$. Can this be deduced from Lemma 6 (and suitable mollification)?
13 November, 2015 at 9:59 am
Terence Tao
If the space is locally compact Hausdorff, then any open cover will have a partition of unity with compactly supported functions, and the additional conditions in Lemma 6 are not needed. (Actually, this would make a good additional exercise here, which I may add to a future edition of the text.) But in the normal case, I believe some condition like this is necessary.
One can obtain a smooth partition of unity from a continuous one by convolving all the functions by an smooth approximation to the identity (with the exact choice of mollifier dependent on the location, as the open sets may become increasingly small in diameter at infinity), and then dividing out by the sum as before in order to recover the property of summing to one.
2 December, 2015 at 7:08 am
Anonymous
In the proof of the Urysohn lemma, can
be replaced with
or
[Yes, although these descriptions of are not as useful as the first two for establishing continuity. -T.]
are not as useful as the first two for establishing continuity. -T.]
25 February, 2016 at 4:37 pm
Anonymous
Do you have a reference for part 4 (The commutative Gelfand-Naimark theorem (optional) ) in this note which is also similar to the way you represent it?
26 February, 2016 at 9:38 am
Terence Tao
I adapted this material from various texts on non-commutative Gelfand theory (of which there are several), specialising to the commutative case. I don’t know of a text that focuses primarily on the commutative case though.
25 February, 2016 at 5:43 pm
Anonymous
Does the “spectrum” in Definition 16 have anything to do with the one in https://en.wikipedia.org/wiki/Spectrum_(functional_analysis)#Definition
?
26 February, 2016 at 9:33 am
Terence Tao
This is the Gelfand spectrum: https://en.wikipedia.org/wiki/Gelfand_representation#The_spectrum_of_a_commutative_C.2A-algebra of a function space, rather than the spectrum of a linear operator. In some cases there is a relationship; for instance the Gelfand spectrum of the convolution algebra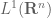 is naturally associated to the joint spectrum of the infinitesimal translation operators
is naturally associated to the joint spectrum of the infinitesimal translation operators  . In particular, both concepts can be viewed as capturing a notion of the available “frequencies” in a function space or linear operator. However in general there is not much of a direct relationship between the two.
. In particular, both concepts can be viewed as capturing a notion of the available “frequencies” in a function space or linear operator. However in general there is not much of a direct relationship between the two.
28 February, 2016 at 3:35 pm
Anonymous
In http://math.oregonstate.edu/~holladwi/banach_algebras.pdf , the Gelfand-Naimark Theorem (Theorem 50) is called as the “abstract spectral theorem”, in which the spectrum is the set of characters. Then Gelfand-Naimark is used in the proof of Theorem 51 (spectral theorem), in which the spectrum of a linear operator appears.
Is this also related to what you said in the comment?
25 February, 2016 at 7:32 pm
Anonymous
Do Definition 16 and Exercise 39 remain the same if one replaces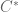 -algebra with Banach-algebra and drops the condition
-algebra with Banach-algebra and drops the condition  ?
?
26 February, 2016 at 9:37 am
Terence Tao
I believe one can prove something of this form with the aid of the Riesz representation theorem, but I haven’t checked the details.
28 June, 2016 at 12:04 am
Nick
Exercise 11 does not need to hold for non-Hausdorff . A counterexample being the two point space with one point being open but not closed. All continuous functions are constant, but there are nonconstant semicontinuos ones.
. A counterexample being the two point space with one point being open but not closed. All continuous functions are constant, but there are nonconstant semicontinuos ones.
29 June, 2016 at 6:54 am
Terence Tao
Sorry, could you elaborate on why this is a counterexample to either part of Exercise 11? Note that part 2 of this exercise has the additional assumption that is normal.
is normal.
29 June, 2016 at 9:41 am
Nick
It’s a little nitpicky, but by the definition given in these notes, this space is normal (while not fulfilling part 2). It is just required that you can separate disjoint closed sets by disjoint open neighborhoods, which is automatically the case here, since one of the closed sets must be empty.
[Ah, I see now. Correction added, thanks – T.]
12 November, 2016 at 4:44 am
zhche
Dear Prof Tao,
As for exercise 15, the uniqueness of the minimal decomposition is quite easy to prove. But for the existence part, I think for any two different decompositions and
and  , they only need to satisfy that difference
, they only need to satisfy that difference  is a linear functional, not necessarily the value
is a linear functional, not necessarily the value 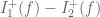 be positive for each
be positive for each  in
in  . Then the sense of ordering does not necessarily for any two decompositions, i.e., there may be no minimal decompositions. Am I understanding right ?
. Then the sense of ordering does not necessarily for any two decompositions, i.e., there may be no minimal decompositions. Am I understanding right ?
Regards
Che Zhihua
[It is possible for a partial order to have a minimal element even if it fails to be a total order. For instance, the set of all subsets of a given set (partially ordered by set inclusion) has a minimal element
(partially ordered by set inclusion) has a minimal element  even though most pairs
even though most pairs 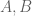 of subsets of
of subsets of  are incomparable. -T.]
are incomparable. -T.]
13 November, 2016 at 5:06 am
zhche
Yes, I found it partial order. So this exercise means to want us to prove that this poset HAS a least element, e.g., prove it is bounded lattice ? Then this exercise is not that trivial.
4 December, 2016 at 12:07 am
Ian
Professor Tao:
Concerning the proof of Lusin’s Theorem, could you please explain the use of Exercise 10? It seems to me that this exercise produces a function that agrees with only in (most of) its compact support, but doesn’t really guarantee anything on the whole space.
only in (most of) its compact support, but doesn’t really guarantee anything on the whole space.
4 December, 2016 at 1:22 pm
Terence Tao
One can multiply the function produced by Exercise 10 with a cutoff function coming from Urysohn’s lemma to make the support of that function only slightly larger than the support of .
.
17 February, 2017 at 9:57 pm
254A, Notes 2: The central limit theorem | What's new
[…] distribution (this is a consequence of the Riesz representation theorem, discussed for instance in this blog post). As a consequence of the insensitivity of convergence in distribution to equivalence in […]
16 January, 2019 at 8:51 am
245A: Problem solving strategies | What's new
[…] is true for a class of functions that is large enough to separate points in the space, so that the Stone-Weierstrass theorem may be […]
11 March, 2019 at 11:37 pm
Maths student
Dear Prof. Tao (or anyone reading this),
the proof of Riesz’ theorem that you gave relied on the -compactness hypothesis, because only this hypothesis allowed the transition from the compact to the general case. Is it true that one might drop this hypothesis by resorting to more general means of summation (such as integration against a counting measure)?
-compactness hypothesis, because only this hypothesis allowed the transition from the compact to the general case. Is it true that one might drop this hypothesis by resorting to more general means of summation (such as integration against a counting measure)?
6 February, 2020 at 5:30 pm
Anonymous
I have seen a (quite short) proof of Theorem 10 (the complex version) using Zorn’s lemma. But I can only remember the beginning.
Let and one wants to show that
and one wants to show that  . The proof draws a contradiction by assuming that
. The proof draws a contradiction by assuming that 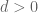 .
.
It then defines for any closed that
that
Define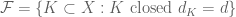 .
.
Zorn’s lemma implies (I don’t know how) that there exists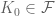 minimal with respect to
minimal with respect to 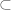 and
and  is not a singleton.
is not a singleton.
Do anyone know how to finish the proof and where is it possibly from?
5 April, 2022 at 12:08 am
Anonymous
Dear Prof.Tao: Is Exercise 7 incorrect? Consider the dirac measure at some point as the Radon measure on real line. Then it seems the convergence in $L^\infty$ only controls the convergence at this point.
5 April, 2022 at 3:03 pm
Terence Tao
Actually, the statement is still true in this case! (But one needs the Tietze extension theorem, which is not covered at this stage of the notes, and so this exercise needs to be moved. See the erratum to the book version of this exercise (Exercise 1.10.7) at https://terrytao.wordpress.com/books/an-epsilon-of-room-pages-from-year-three-of-a-mathematical-blog/
6 April, 2022 at 1:37 am
Anonymous
Dear Prof.Tao. How to construct a closed subset as support of measure such that every open set(non-empty) has positive measure. If we just take the union of all open set in $X$ having null measure and the complement of this union is closed but may not be co-null(since this may be an uncountable union), if we just assume second countability, this is OK(but in general locally compact and sigma-compact Hausdorff space may be not normal). But I still don’t understand how to use Tietz extension(since $X$ may be not normal,and if we take one-point Alexandroff compactification, then the closed set may be not closed any more). Also how Tietz extension controls the growth at infinity? Would you elaborate more? It seems this problem has been posted also here :https://math.stackexchange.com/questions/1576634/the-closure-of-c-c-in-l-infty-is-c-0 But the discussion seems not conclusive.
24 April, 2022 at 5:18 am
Anonymous
Is Exercise15 correct?Whether should be positive instead?
should be positive instead?
[Corrected, thanks – T.]
25 April, 2022 at 9:20 am
Anonymous
It is correct. need not be positive.
need not be positive.
16 February, 2023 at 6:53 pm
Anonymous
Perhaps the Wikipedia page linked to Riesz representation theorem should be https://en.wikipedia.org/wiki/Riesz–Markov–Kakutani_representation_theorem rather than the one related to Hilbert space?