A fundamental tool in any mathematician’s toolkit is that of reductio ad absurdum: showing that a statement is false by assuming first that
is true, and showing that this leads to a logical contradiction. A particulary pure example of reductio ad absurdum occurs when establishing the non-existence of a hypothetically overpowered object or structure
, by showing that
‘s powers are “self-defeating”: the very existence of
and its powers can be used (by some clever trick) to construct a counterexample to that power. Perhaps the most well-known example of a self-defeating object comes from the omnipotence paradox in philosophy (“Can an omnipotent being create a rock so heavy that He cannot lift it?”); more generally, a large number of other paradoxes in logic or philosophy can be reinterpreted as a proof that a certain overpowered object or structure does not exist.
In mathematics, perhaps the first example of a self-defeating object one encounters is that of a largest natural number:
Proposition 1 (No largest natural number) There does not exist a natural number
which is larger than all other natural numbers.
Proof: Suppose for contradiction that there was such a largest natural number . Then
is also a natural number which is strictly larger than
, contradicting the hypothesis that
is the largest natural number.
Note the argument does not apply to the extended natural number system in which one adjoins an additional object beyond the natural numbers, because
is defined equal to
. However, the above argument does show that the existence of a largest number is not compatible with the Peano axioms.
This argument, by the way, is perhaps the only mathematical argument I know of which is routinely taught to primary school children by other primary school children, thanks to the schoolyard game of naming the largest number. It is arguably one’s first exposure to a mathematical non-existence result, which seems innocuous at first but can be surprisingly deep, as such results preclude in advance all future attempts to establish existence of that object, no matter how much effort or ingenuity is poured into this task. One sees this in a typical instance of the above schoolyard game; one player tries furiously to cleverly construct some impressively huge number , but no matter how much effort is expended in doing so, the player is defeated by the simple response “… plus one!” (unless, of course,
is infinite, ill-defined, or otherwise not a natural number).
It is not only individual objects (such as natural numbers) which can be self-defeating; structures (such as orderings or enumerations) can also be self-defeating. (In modern set theory, one considers structures to themselves be a kind of object, and so the distinction between the two concepts is often blurred.) Here is one example (related to, but subtly different from, the previous one):
Proposition 2 (The natural numbers cannot be finitely enumerated) The natural numbers
cannot be written as
for any finite collection
of natural numbers.
Proof: Suppose for contradiction that such an enumeration existed. Then consider the number
; this is a natural number, but is larger than (and hence not equal to) any of the natural numbers
, contradicting the hypothesis that
is enumerated by
.
Here it is the enumeration which is self-defeating, rather than any individual natural number such as or
. (For this post, we allow enumerations to contain repetitions.)
The above argument may seem trivial, but a slight modification of it already gives an important result, namely Euclid’s theorem:
Proposition 3 (The primes cannot be finitely enumerated) The prime numbers
cannot be written as
for any finite collection of prime numbers.
Proof: Suppose for contradiction that such an enumeration existed. Then consider the natural number
; this is a natural number larger than
which is not divisible by any of the primes
. But, by the fundamental theorem of arithmetic (or by the method of Infinite descent, which is another classic application of reductio ad absurdum), every natural number larger than
must be divisible by some prime, contradicting the hypothesis that
is enumerated by
.
Remark 1 Continuing the number-theoretic theme, the “dueling conspiracies” arguments in a previous blog post can also be viewed as an instance of this type of “no-self-defeating-object”; for instance, a zero of the Riemann zeta function at
implies that the primes anti-correlate almost completely with the multiplicative function
, which is self-defeating because it also implies complete anti-correlation with
, and the two are incompatible. Thus we see that the prime number theorem (a much stronger version of Proposition 3) also emerges from this type of argument.
In this post I would like to collect several other well-known examples of this type of “no self-defeating object” argument. Each of these is well studied, and probably quite familiar to many of you, but I feel that by collecting them all in one place, the commonality of theme between these arguments becomes more apparent. (For instance, as we shall see, many well-known “paradoxes” in logic and philosophy can be interpreted mathematically as a rigorous “no self-defeating object” argument.)
— 1. Set theory —
Many famous foundational results in set theory come from a “no self-defeating object” argument. (Here, we shall be implicitly be using a standard axiomatic framework for set theory, such as Zermelo-Frankel set theory; the situation becomes different for other set theories, much as results such as Proposition 1 changes if one uses other number systems such as the extended natural numbers.) The basic idea here is that any sufficiently overpowered set-theoretic object is capable of encoding a version of the liar paradox (“this sentence is false”, or more generally a statement which can be shown to be logically equivalent to its negation) and thus lead to a contradiction. Consider for instance this variant of Russell’s paradox:
Proposition 4 (No universal set) There does not exist a set which contains all sets (including itself).
Proof: Suppose for contradiction that there existed a universal set which contained all sets. Using the axiom schema of specification, one can then construct the set
of all sets in the universe which did not contain themselves. As is universal,
is contained in
. But then, by definition of
, one sees that
if and only if
, a contradiction.
Remark 2 As a corollary, there also does not exist any set
which contains all other sets (not including itself), because the set
would then be universal.
One can “localise” the above argument to a smaller domain than the entire universe, leading to the important
Proposition 5 (Cantor’s theorem) Let
be a set. Then the power set
of
cannot be enumerated by
, i.e. one cannot write
for some collection
of subsets of
.
Proof: Suppose for contradiction that there existed a set whose power set
could be enumerated as
for some
. Using the axiom schema of specification, one can then construct the set
The set is an element of the power set
. As
is enumerated by
, we have
for some
. But then by the definition of
, one sees that
if and only if
, a contradiction.
As is well-known, one can adapt Cantor’s argument to the real line, showing that the reals are uncountable:
Proposition 6 (The real numbers cannot be countably enumerated) The real numbers
cannot be written as
for any countable collection
of real numbers.
Proof: Suppose for contradiction that there existed a countable enumeration of by a sequence
of real numbers. Consider the decimal expansion of each of these numbers. Note that, due to the well-known “
” issue, the decimal expansion may be non-unique, but each real number
has at most two decimal expansions. For each
, let
be a digit which is not equal to the
digit of any of the decimal expansions of
; this is always possible because there are ten digits to choose from and at most two decimal expansions of
. (One can avoid any implicit invocation of the axiom of choice here by setting
to be (say) the least digit which is not equal to the
digit of any of the decimal expansions of
.) Then the real number given by the decimal expansion
differs in the
digit from any of the decimal expansions of
for each
, and so is distinct from every
, a contradiction.
Remark 3 One can of course deduce Proposition 6 directly from Proposition 5, by using the decimal representation to embed
into
. But notice how the two arguments have a slightly different (though closely related) basis; the former argument proceeds by encoding the liar paradox, while the second proceeds by exploiting Cantor’s diagonal argument. The two perspectives are indeed a little different: for instance, Cantor’s diagonal argument can also be modified to establish the Arzela-Ascolí theorem, whereas I do not see any obvious way to prove that theorem by encoding the liar paradox.
Remark 4 It is an interesting psychological phenomenon that Proposition 6 is often considered far more unintuitive than any of the other propositions here, despite being in the same family of arguments; most people have no objection to the fact that every effort to finitely enumerate the natural numbers, for instance, is doomed to failure, but for some reason it is much harder to let go of the belief that, at some point, some sufficiently ingenious person will work out a way to countably enumerate the real numbers. I am not exactly sure why this disparity exists, but I suspect it is at least partly due to the fact that the rigorous construction of the real numbers is quite sophisticated and often not presented properly until the advanced undergraduate level. (Or perhaps it is because we do not play the game “enumerate the real numbers” often enough in schoolyards.)
Remark 5 One can also use the diagonal argument to show that any reasonable notion of a “constructible real number” must itself be non-constructive (this is related to the interesting number paradox). Part of the problem is that the question of determining whether a proposed construction of a real number is actually well-defined is a variant of the halting problem, which we will discuss below.
While a genuinely universal set is not possible in standard set theory, one at least has the notion of an ordinal, which contains all the ordinals less than it. (In the discussion below, we assume familiarity with the theory of ordinals.) One can modify the above arguments concerning sets to give analogous results about the ordinals. For instance:
Proposition 7 (Ordinals do not form a set) There does not exist a set that contains all the ordinals.
Proof: Suppose for contradiction that such a set existed. By the axiom schema of specification, one can then find a set which consists precisely of all the ordinals and nothing else. But then
is an ordinal which is not contained in
(by the axiom of foundation, also known as the axiom of regularity), a contradiction.
Remark 6 This proposition(together with the theory of ordinals) can be used to give a quick proof of Zorn’s lemma: see these lecture notes of mine for further discussion. Notice the similarity between this argument and the proof of Proposition 1.
Remark 7 Once one has Zorn’s lemma, one can show that various other classes of mathematical objects do not form sets. Consider for instance the class of all vector spaces. Observe that any chain of (real) vector spaces (ordered by inclusion) has an upper bound (namely the union or limit of these spaces); thus, if the class of all vector spaces was a set, then Zorn’s lemma would imply the existence of a maximal vector space
. But one can simply adjoin an additional element not already in
(e.g.
) to
, and contradict this maximality. (An alternate proof: every object is an element of some vector space, and in particular every set is an element of some vector space. If the class of all vector spaces formed a set, then by the axiom of union, we see that union of all vector spaces is a set also, contradicting Proposition 4.)
One can localise the above argument to smaller cardinalities, for instance:
Proposition 8 (Countable ordinals are uncountable) There does not exist a countable enumeration
of the countable ordinals. (Here we consider finite sets and countably infinite sets to both be countable.)
Proof: Suppose for contradiction that there exists a countable enumeration of the countable ordinals. Then the set
is also a countable ordinal, as is the set
. But
is not equal to any of the
(by the axiom of foundation), a contradiction.
Remark 8 One can show the existence of uncountable ordinals (e.g. by considering all the well-orderings of subsets of the natural numbers, up to isomorphism), and then there exists a least uncountable ordinal
. By construction, this ordinal consists precisely of all the countable ordinals, but is itself uncountable, much as
consists precisely of all the finite natural numbers, but is itself infinite (Proposition 2). The least uncountable ordinal is notorious, among other things, for providing a host of counterexamples to various intuitively plausible assertions in point set topology, and in particular in showing that the topology of sufficiently uncountable spaces cannot always be adequately explored by countable objects such as sequences.
Remark 9 The existence of the least uncountable ordinal can explain why one cannot contradict Cantor’s theorem on the uncountability of the reals simply by iterating the diagonal argument (or any other algorithm) in an attempt to “exhaust” the reals. From transfinite induction we see that the diagonal argument allows one to assign a different real number to each countable ordinal, but this does not establish countability of the reals, because the set of all countable ordinals is itself uncountable. (This is similar to how one cannot contradict Proposition 4 by iterating the
map, as the set of all finite natural numbers is itself infinite.) In any event, even once one reaches the first uncountable ordinal, one may not yet have completely exhausted the reals; for instance, using the diagonal argument given in the proof of Proposition 6, only the real numbers in the interval
will ever be enumerated by this procedure. (Also, the question of whether all real numbers in
can be enumerated by the iterated diagonal algorithm requires the continuum hypothesis, and even with this hypothesis I am not sure whether the statement is decidable.)
— 2. Logic —
The “no self-defeating object” argument leads to a number of important non-existence results in logic. Again, the basic idea is to show that a sufficiently overpowered logical structure will eventually lead to the existence of a self-contradictory statement, such as the liar paradox. To state examples of this properly, one unfortunately has to invest a fair amount of time in first carefully setting up the language and theory of logic. I will not do so here, and instead use informal English sentences as a proxy for precise logical statements to convey a taste (but not a completely rigorous description) of these logical results here.
The liar paradox itself – the inability to assign a consistent truth value to “this sentence is false” – can be viewed as an argument demonstrating that there is no consistent way to interpret (i.e. assign a truth value to) sentences, when the sentences are (a) allowed to be self-referential, and (b) allowed to invoke the very notion of truth given by this interpretation. One’s first impulse is to say that the difficulty here lies more with (a) than with (b), but there is a clever trick, known as Quining (or indirect self-reference), which allows one to modify the liar paradox to produce a non-self-referential statement to which one still cannot assign a consistent truth value. The idea is to work not with fully formed sentences , which have a single truth value, but instead with predicates
, whose truth value depends on a variable
in some range. For instance,
may be “
is two characters long.”, and the range of
may be the set of strings (i.e. finite sequences of characters); then for every string
, the statement
(formed by replacing every appearance of
in
with
) is either true or false. For instance,
is true, but
is false. Crucially, predicates are themselves strings, and can thus be fed into themselves as input; for instance,
is false. If however
is the predicate “
is sixty-five characters long.”, observe that
is true.
Now consider the Quine predicate given by
“ is a predicate whose range is the set of strings, and
is false.”
whose range is the set of strings. Thus, for any string ,
is the sentence
“ is a predicate whose range is the set of strings, and
is false.”
This predicate is defined non-recursively, but the sentence captures the essence of the liar paradox: it is true if and only if it is false. This shows that there is no consistent way to interpret sentences in which the sentences are allowed to come from predicates, are allowed to use the concept of a string, and also allowed to use the concept of truth as given by that interpretation.
Note that the proof of Proposition 4 is basically the set-theoretic analogue of the above argument, with the connection being that one can identify a predicate with the set
.
By making one small modification to the above argument – replacing the notion of truth with the related notion of provability – one obtains the celebrated Gödel’s (second) incompleteness theorem:
Theorem 9 (Gödel’s incompleteness theorem) (Informal statement) No consistent logical system which has the notion of a string, can provide a proof of its own logical consistency. (Note that a proof can be viewed as a certain type of string.)
Remark 10 Because one can encode strings in numerical form (e.g. using the ASCII code), it is also true (informally speaking) that no consistent logical system which has the notion of a natural number, can provide a proof of its own logical consistency.
Proof: (Informal sketch only) Suppose for contradiction that one had a consistent logical system inside of which its consistency could be proven. Now let be the predicate given by
“ is a predicate whose range is the set of strings, and
is not provable”
and whose range is the set of strings. Define the Gödel sentence to be the string
. Then
is logically equivalent to the assertion “
is not provable”. Thus, if
were false, then
would be provable, which (by the consistency of the system) implies that
is true, a contradiction; thus,
must be true. Because the system is provably consistent, the above argument can be placed inside the system itself, to prove inside that system that
must be true; thus
is provable and
is then false, a contradiction. (It becomes quite necessary to carefully distinguish the notions of truth and provability (both inside a system and externally to that system) in order to get this argument straight!)
Remark 11 It is not hard to show that a consistent logical system which can model the standard natural numbers cannot disprove its own consistency either (i.e. it cannot establish the statement that one can deduce a contradiction from the axioms in the systems in
steps for some natural number
); thus the consistency of such a system is undecidable within that system. Thus this theorem strengthens the (more well known) first Gödel incompleteness theorem, which asserts the existence of undecidable statements inside a consistent logical system which contains the concept of a string (or a natural number). On the other hand, the incompleteness theorem does not preclude the possibility that the consistency of a weak theory could be proven in a strictly stronger theory (e.g. the consistency of Peano arithmetic is provable in Zermelo-Frankel set theory).
Remark 12 One can use the incompleteness theorem to establish the undecidability of other overpowered problems. For instance, Matiyasevich’s theorem demonstrates that the problem of determining the solvability of a system of Diophantine equations is, in general, undecidable, because one can encode statements such as the consistency of set theory inside such a system.
— 3. Computability —
One can adapt these arguments in logic to analogous arguments in the theory of computation; the basic idea here is to show that a sufficiently overpowered computer program cannot exist, by feeding the source code for that program into the program itself (or some slight modification thereof) to create a contradiction. As with logic, a properly rigorous formalisation of the theory of computation would require a fair amount of preliminary machinery, for instance to define the concept of Turing machine (or some other universal computer), and so I will once again use informal English sentences as an informal substitute for a precise programming language.
A fundamental “no self-defeating object” argument in the subject, analogous to the other liar paradox type arguments encountered previously, is the Turing halting theorem:
Theorem 10 (Turing halting theorem) There does not exist a program
which takes a string
as input, and determines in finite time whether
is a program (with no input) that halts in finite time.
Proof: Suppose for contradiction that such a program existed. Then one could easily modify
to create a variant program
, which takes a string
as input, and halts if and only if
is a program (with
itself as input) that does not halts in finite time. Indeed, all
has to do is call
with the string
, defined as the program (with no input) formed by declaring
to be the input string for the program
. If
determines that
does not halt, then
halts; otherwise, if
determines that
does halt, then
performs an infinite loop and does not halt. Then observe that
will halt if and only if it does not halt, a contradiction.
Remark 13 As one can imagine from the proofs, this result is closely related to, but not quite identical with, the Gödel incompleteness theorem. That latter theorem implies that the question of whether a given program halts or not in general is undecidable (consider a program designed to search for proofs of the inconsistency of set theory). By contrast, the halting theorem (roughly speaking) shows that this question is uncomputable (i.e. there is no algorithm to decide halting in general) rather than undecidable (i.e. there are programs whose halting can neither be proven nor disproven).
On the other hand, the halting theorem can be used to establish the incompleteness theorem. Indeed, suppose that all statements in a suitably strong and consistent logical system were either provable or disprovable. Then one could build a program that determined whether an input string
, when run as a program, halts in finite time, simply by searching for all proofs or disproofs of the statement “
halts in finite time”; this program is guaranteed to terminate with a correct answer by hypothesis.
Remark 14 While it is not possible for the halting problem for a given computing language to be computable in that language, it is certainly possible that it is computable in a strictly stronger language. When that is the case, one can then invoke Newcomb’s paradox to argue that the weaker language does not have unlimited “free will” in some sense.
Remark 15 In the language of recursion theory, the halting theorem asserts that the set of programs that do not halt is not a decidable set (or a recursive set). In fact, one can make the slightly stronger assertion that the set of programs that do not halt is not even a semi-decidable set (or a recursively enumerable set), i.e. there is no algorithm which takes a program as input and halts in finite time if and only if the input program does not halt. This is because the complementary set of programs that do halt is clearly semi-decidable (one simply runs the program until it halts, running forever if it does not), and so if the set of programs that do not halt is also semi-decidable, then it is decidable (by running both algorithms in parallel; this observation is a special case of Post’s theorem).
Remark 16 One can use the halting theorem to exclude overly general theories for certain types of mathematical objects. For instance, one cannot hope to find an algorithm to determine the existence of smooth solutions to arbitrary nonlinear partial differential equations, because it is possible to simulate a Turing machine using the laws of classical physics, which in turn can be modeled using (a moderately complicated system of) nonlinear PDE. Instead, progress in nonlinear PDE has instead proceeded by focusing on much more specific classes of such PDE (e.g. elliptic PDE, parabolic PDE, hyperbolic PDE, gauge theories, etc.).
One can place the halting theorem in a more “quantitative” form. Call a function computable if there exists a computer program which, when given a natural number
as input, returns
as output in finite time. Define the Busy Beaver function
by setting
to equal the largest output of any program of at most
characters in length (and taking no input), which halts in finite time. Note that there are only finitely many such programs for any given
, so
is well-defined. On the other hand, it is uncomputable, even to upper bound:
Proposition 11 There does not exist a computable function
such that one has
for all
.
Proof: Suppose for contradiction that there existed a computable function such that
for all
. We can use this to contradict the halting theorem, as follows. First observe that once the Busy Beaver function can be upper bounded by a computable function, then for any
, the run time of any halting program of length at most
can also be upper bounded by a computable function. This is because if a program of length
halts in finite time, then a trivial modification of that program (of length larger than
, but by a computable factor) is capable of outputting the run time of that program (by keeping track of a suitable “clock” variable, for instance). Applying the upper bound for Busy Beaver to that increased length, one obtains the bound on run time.
Now, to determine whether a given program halts in finite time or not, one simply simulates (runs) that program for time up to the computable upper bound of the possible running time of
, given by the length of
. If the program has not halted by then, then it never will. This provides a program
obeying the hypotheses of the halting theorem, a contradiction.
Remark 17 A variant of the argument shows that
grows faster than any computable function: thus if
is computable, then
for all sufficiently large
. We leave the proof of this result as an exercise to the reader.
Remark 18 Sadly, the most important unsolved problem in complexity theory, namely the
problem, does not seem to be susceptible to the no-self-defeating-object argument, basically because such arguments tend to be relativisable whereas the
problem is not; see this earlier blog post for more discussion. On the other hand, one has the curious feature that many proposed proofs that
appear to be self-defeating; this is most strikingly captured in the celebrated work of Razborov and Rudich, who showed (very roughly speaking) that any sufficiently “natural” proof that
could be used to disprove the existence of an object closely related to the belief that
, namely the existence of pseudorandom number generators. (I am told, though, that diagonalisation arguments can be used to prove some other inclusions or non-inclusions in complexity theory that are not subject to the relativisation barrier, though I do not know the details.)
— 4. Game theory —
Another basic example of the no-self-defeating-objects argument arises from game theory, namely the strategy stealing argument. Consider for instance a generalised version of naughts and crosses (tic-tac-toe), in which two players take turns placing naughts and crosses on some game board (not necessarily square, and not necessarily two-dimensional), with the naughts player going first, until a certain pattern of all naughts or all crosses is obtained as a subpattern, with the naughts player winning if the pattern is all naughts, and the crosses player winning if the pattern is all crosses. (If all positions are filled without either pattern occurring, the game is a draw.) We assume that the winning patterns for the cross player are exactly the same as the winning patterns for the naughts player (but with naughts replaced by crosses, of course).
Proposition 12 In any generalised version of naughts and crosses, there is no strategy for the second player (i.e. the crosses player) which is guaranteed to ensure victory.
Proof: Suppose for contradiction that the second player had such a winning strategy . The first player can then steal that strategy by placing a naught arbitrarily on the board, and then pretending to be the second player and using
accordingly. Note that occasionally, the
strategy will compel the naughts player to place a naught on the square that he or she has already occupied, but in such cases the naughts player may simply place the naught somewhere else instead. (It is not possible that the naughts player would run out of places, thus forcing a draw, because this would imply that
could lead to a draw as well, a contradiction.) If we denote this stolen strategy by
, then
guarantees a win for the naughts player; playing the
strategy for the naughts player against the
strategy for the crosses player, we obtain a contradiction.
Remark 19 The key point here is that in naughts and crosses games, it is possible to play a harmless move – a move which gives up the turn of play, but does not actually decrease one’s chance of winning. In games such as chess, there does not appear to be any analogue of the harmless move, and so it is not known whether black actually has a strategy guaranteed to win or not in chess, though it is suspected that this is not the case.
Remark 20 The Hales-Jewett theorem shows that for any fixed board length, an
-dimensional game of naughts and crosses is unable to end in a draw if
is sufficiently large. An induction argument shows that for any two-player game that terminates in bounded time in which draws are impossible, one player must have a guaranteed winning strategy; by the above proposition, this strategy must be a win for the naughts player. Note, however, that Proposition 12 provides no information as to how to locate this winning strategy, other than that this strategy belongs to the naughts player. Nevertheless, this gives a second example in which the no-self-defeating-object argument can be used to ensure the existence of some object, rather than the non-existence of an object. (The first example was the prime number theorem, discussed earlier.)
The strategy-stealing argument can be applied to real-world economics and finance, though as with any other application of mathematics to the real world, one has to be careful as to the implicit assumptions one is making about reality and how it conforms to one’s mathematical model when doing so. For instance, one can argue that in any market or other economic system in which the net amount of money is approximately constant, it is not possible to locate a universal trading strategy which is guaranteed to make money for the user of that strategy, since if everyone applied that strategy then the net amount of money in the system would increase, a contradiction. Note however that there are many loopholes here; it may be that the strategy is difficult to copy, or relies on exploiting some other group of participants who are unaware or unable to use the strategy, and would then lose money (though in such a case, the strategy is not truly universal as it would stop working once enough people used it). Unfortunately, there can be strong psychological factors that can cause people to override the conclusions of such strategy-stealing arguments with their own rationalisations, as can be seen, for instance, in the perennial popularity of pyramid schemes, or to a lesser extent, market bubbles (though one has to be careful about applying the strategy-stealing argument in the latter case, since it is possible to have net wealth creation through external factors such as advances in technology).
Note also that the strategy-stealing argument also limits the universal predictive power of technical analysis to provide predictions other than that the prices obey a martingale, though again there are loopholes in the case of markets that are illiquid or highly volatile.
— 5. Physics —
In a similar vein, one can try to adapt the no-self-defeating-object argument from mathematics to physics, but again one has to be much more careful with various physical and metaphysical assumptions that may be implicit in one’s argument. For instance, one can argue that under the laws of special relativity, it is not possible to construct a totally immovable object. The argument would be that if one could construct an immovable object in one inertial reference frame, then by the principle of relativity it should be possible to construct an object
which is immovable in another inertial reference frame which is moving with respect to the first; setting the two on a collision course, we obtain the classic contradiction between an irresistible force and an immovable object. Note however that there are several loopholes here which allow one to avoid contradiction; for instance, the two objects
could simply pass through each other without interacting.
In a somewhat similar vein, using the laws of special relativity one can argue that it is not possible to systematically generate and detect tachyon particles – particles traveling faster than the speed of light – because these could be used to transmit localised information faster than the speed of light, and then (by the principle of relativity) to send localised information back into the past, from one location to a distant one. Setting up a second tachyon beam to reflect this information back to the original location, one could then send localised information back to one’s own past (rather than to the past of an observer at a distant location), allowing one to set up a classic grandfather paradox. However, as before, there are a large number of loopholes in this argument which could let one avoid contradiction; for instance, if the apparatus needed to set up the tachyon beam may be larger than the distance the beam travels (as is for instance the case in Mexican wave-type tachyon beams) then there is no causality paradox; another loophole is if the tachyon beam is not fully localised, but propagates in spacetime in a manner to interfere with the second tachyon beam. A third loophole occurs if the universe exhibits quantum behaviour (in particular, the ability to exist in entangled states) instead of non-quantum behaviour, which allows for such superluminal mechanisms as wave function collapse to occur without any threat to causality or the principle of relativity. A fourth loophole occurs if the effects of relativistic gravity (i.e. general relativity) become significant. Nevertheless, the paradoxical effect of time travel is so strong that this physical argument is a fairly convincing way to rule out many commonly imagined types of faster-than-light travel or communication (and we have a number of other arguments too that exclude more modes of faster-than-light behaviour, though this is an entire blog post topic in its own right).

95 comments
Comments feed for this article
23 October, 2011 at 8:17 am
Ray Cheung
About the proof for Theorem 10 (Halting problem):
Why doesn’t the proof show only that it is impossible for Q to exist? If P -> Q, and Q leads to a contradiction, P is impossible – which I suppose is what the proof is. However, it is unclear to me why P -> Q.
If, on the other hand, the proof is supposed to use Q as a counterexample to P’s ability in determining whether a programme halts (for all programmes), one may simply reply that Q is not a (possible) programme.
23 October, 2011 at 8:26 am
Terence Tao
The third and fourth sentences of the proof describe how the existence of a program P that can solve the halting problem implies the existence of a program Q that halts on S iff S(S) does not halt. Because of this implication, the non-existence of the latter program implies the nonexistence of the former program.
23 October, 2011 at 8:21 am
Ray Cheung
Sorry: “P -> Q” reads if P exists, Q exists, etc
20 March, 2012 at 3:47 pm
Carnival of Mathematics #59 « The Number Warrior
[…] Can an omnipotent deity create a rock he can’t lift? Terry Tao tackles mathematical equivalents when considering the “no self-defeating object” argument. […]
20 May, 2012 at 2:58 pm
Heuristic limitations of the circle method « What’s new
[…] be used to conspire against itself (in the spirit of “self-defeating object” arguments, discussed previously several times on this blog). This is actually a fairly common technique in analytic number theory […]
25 August, 2012 at 9:30 am
Trevor Wilson
Dear Professor Tao, I noticed that your proof that the set of countable ordinals is uncountable uses the axiom of choice and in fact proves the stronger statement that omega_1 is regular, for which some some amount of choice is required to prove. But one can prove the original statement in ZF: the set of countable ordinals is itself an ordinal, so if it were countable then it would contain itself as an element.
26 September, 2014 at 4:11 am
My great WordPress blog – Weekend Econlinks
[…] nice recap post of Terry Tao on the “no self-defeating object” argument in mathematical […]
31 August, 2017 at 8:02 am
Diagonal Basilisks: Slashing the Field of Enlightened Intelligence | Conflated Automatons
[…] Tao describes Cantor’s diagonal proof as belonging to a loose collection of “no self-defeating object” arguments, where “the very existence of {X} and its powers can be used (by some clever trick) to construct […]
30 September, 2017 at 8:16 pm
Toby Bartels
Rather late to the party, but … using Zorn’s Lemma to prove that the class of all vector spaces is a proper class seems like using the proverbial sledgehammer to kill a fly, since already the class of all *zero-dimensional* vector spaces is proper! Any such vector space has an element, and that element could be anything at all, so once you have any proper class whatsoever (which we have by this point in the article), then you have a proper class of zero-dimensional vector spaces. (To avoid using Replacement, consider the union of the underlying sets of the vector spaces.)
1 October, 2017 at 8:26 am
Aula
No, the class of zero-dimensional vector spaces is a set of exactly one element, namely the unique zero-dimensional vector space which in turn contains the unique zero-length vector.
9 October, 2017 at 1:10 pm
Toby Bartels
That’s a fine way to look at things, but it’s not how it works with abstract vector spaces in ZFC. Feel free to use a less abstract notion of vector space or even a different foundation of mathematics, but can you come up with a way in which Terry’s argument (involving unions of chains of vector spaces) proves a nontrivial theorem?
17 October, 2017 at 9:49 am
Terence Tao
The same argument also shows, for instance, that there is no moduli space for vector spaces up to isomorphism which is a set. (Though this stronger assertion does require some version of Cantor’s theorem to show that there is no vector space that is maximal modulo isomorphism.)
29 November, 2019 at 9:34 am
Arunava mondal
Prof terence tao and math seems like made for each other. wonderful problem solving skills by worlds greatest mathematician ever.
28 February, 2024 at 1:16 am
Anonymous
Proposed large cardinals that turned out to be inconsistent sound like possible examples of self-defeating objects. The most famous of which is Reinhardt’s axiom proposed in 1967, which is that, when is the class of all sets, there is a cardinal
is the class of all sets, there is a cardinal  and a mapping
and a mapping  where
where  , such that
, such that  preserves truth of first-order formulae in the language of set theory. (Such
preserves truth of first-order formulae in the language of set theory. (Such  is called an “elementary embedding from
is called an “elementary embedding from  .) For example,
.) For example,  must equal
must equal 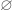 , since if
, since if  is the empty set, then
is the empty set, then  is true, so
is true, so  must be true, therefore
must be true, therefore  must be empty. Similarly for
must be empty. Similarly for 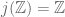 : if
: if 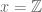 , then
, then  is true, so
is true, so 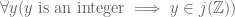 is true, similarly
is true, similarly  ,
,  , etc. In general for any mathematical object which is first-order definable in set theory,
, etc. In general for any mathematical object which is first-order definable in set theory,  is the identity on it. (This reasoning has to be done in MK, as “definability” is not first-order formalizable due to Tarski’s theorem on the undefinability of truth.) For one of Reinhardt’s cardinals
is the identity on it. (This reasoning has to be done in MK, as “definability” is not first-order formalizable due to Tarski’s theorem on the undefinability of truth.) For one of Reinhardt’s cardinals  , the set
, the set  is not equal to
is not equal to  , so such a
, so such a  would be “very undefinable” in that it cannot be singled out by a first-order set-theoretical property. (If it could, the property would hold of
would be “very undefinable” in that it cannot be singled out by a first-order set-theoretical property. (If it could, the property would hold of  too!)
too!)
Four years after it was proposed, Kunen gave a construction of a set which cannot occur in the range of any given such , which means the range of any elementary embedding
, which means the range of any elementary embedding  cannot be $V$. In this way a
cannot be $V$. In this way a  with this property is overpowered as its range is too large. But unlike the self-defeating objects in this blog post, this doesn’t seem to have been shown through a diagonal argument, but instead via infinitary combinatorics. (Additionally Kunen’s proof assumes the axiom of choice, and it is currently an active project in set theory to try to remove this assumption.) However, if restricting only to maps
with this property is overpowered as its range is too large. But unlike the self-defeating objects in this blog post, this doesn’t seem to have been shown through a diagonal argument, but instead via infinitary combinatorics. (Additionally Kunen’s proof assumes the axiom of choice, and it is currently an active project in set theory to try to remove this assumption.) However, if restricting only to maps  that are definable, there is a short proof by contradiction due to Akira Suzuki that fits in seven lines. (V. Dimonte, “I0 and rank-into-rank axioms”, arXiv 1707.02613, theorem 3.12)
that are definable, there is a short proof by contradiction due to Akira Suzuki that fits in seven lines. (V. Dimonte, “I0 and rank-into-rank axioms”, arXiv 1707.02613, theorem 3.12)