In the previous lecture notes, we used (linear) Fourier analysis to control the number of three-term arithmetic progressions in a given set
. The power of the Fourier transform for this problem ultimately stemmed from the identity
for any cyclic group and any subset
of that group (analogues of this identity also exist for other finite abelian groups, and to a lesser extent to non-abelian groups also, although that is not the focus of my current discussion). As it turns out, linear Fourier analysis is not able to discern higher order patterns, such as arithmetic progressions of length four; we give some demonstrations of this below the fold, taking advantage of the polynomial recurrence theory from Notes 1.
The main objective of this course is to introduce the (still nascent) theory of higher order Fourier analysis, which is capable of studying higher order patterns. The full theory is still rather complicated (at least, at our present level of understanding). However, one aspect of the theory is relatively simple, namely that we can largely reduce the study of arbitrary additive patterns to the study of a single type of additive pattern, namely the parallelopipeds
Thus for instance, for one has the line segments
for one has the parallelograms
for one has the parallelopipeds
These patterns are particularly pleasant to handle, thanks to the large number of symmetries available on the discrete cube . For instance, whereas establishing the presence of arbitrarily long arithmetic progressions in dense sets is quite difficult (Szemerédi’s theorem), establishing arbitrarily high-dimensional parallelopipeds is much easier:
Exercise 1 Let
be such that
for some
. If
is sufficiently large depending on
, show that there exists an integer
such that
. (Hint: obtain upper and lower bounds on the set
.)
Exercise 2 (Hilbert cube lemma) Let
be such that
for some
, and let
be an integer. Show that if
is sufficiently large depending on
, then
contains a parallelopiped of the form (2), with
positive integers. (Hint: use the previous exercise and induction.) Conclude that if
has positive upper density, then it contains infinitely many such parallelopipeds for each
.
Exercise 3 Show that if
is an integer, and
is sufficiently large depending on
, then for any parallelopiped (2) in the integers
, there exists
, not all zero, such that
. (Hint: pigeonhole the
in the residue classes modulo
.) Use this to conclude that if
is the set of all integers
such that
for all integers
, then
is a set of positive upper density (and also positive lower density) which does not contain any infinite parallelopipeds (thus one cannot take
in the Hilbert cube lemma).
The standard way to control the parallelogram patterns (and thus, all other (finite complexity) linear patterns) are the Gowers uniformity norms
with a function on a finite abelian group
, and
is the complex conjugation operator; analogues of this norm also exist for group-like objects such as the progression
, and also for measure-preserving systems (where they are known as the Gowers-Host-Kra uniformity seminorms, see this paper of Host-Kra for more discussion). In this set of notes we will focus on the basic properties of these norms; the deepest fact about them, known as the inverse conjecture for these norms, will be discussed in later notes.
— 1. Linear Fourier analysis does not control length four progressions —
Let be a subset of a cyclic group
with density
; we think of
as being fixed, and
as being very large or goingn off to infinity.
For each , consider the number
of -term arithmetic progressions in
(including degenerate progressions). Heuristically, this expression should typically be close to
. Since there are
pairs
and we would expect each pair to have a
“probability” that
simultaneously lie in
. Indeed, using standard probabilistic tools such as Chernoff’s inequality, it is not difficult to justify this heuristic with probability asymptotically close to
in the case that
is a randomly chosen set of the given density.
Let’s see how this heuristic holds up for small values of . For
, this prediction is exactly accurate (with no error term) for any set
with cardinality
; no randomness hypothesis of any sort is required. For
, we see from (1) and the observaation that
that (7) is given by the formula
Let us informally say that is Fourier-pseudorandom if one has
where is a quantity that goes to zero as
. Then from applying Plancherel’s formula and Cauchy-Schwarz as in the previous lecture notes, we see that the number of three-term arithmetic progressions is
Thus we see that the Fourier-pseudorandomness hypothesis allows us to count three-term arithmetic progressions almost exactly.
On the other hand, without the Fourier-pseudorandomness hypothesis, the count (7) can be significantly different from . For instance, if
is an interval
, then it is not hard to see that (7) is comparable to
rather than
; the point is that with a set as structured as an interval, once
and
lie in
, there is already a very strong chance that
lies in
also. In the other direction, a construction of Behrend (mentioned in the previous notes) shows the quantity (7) can in fact dip below
for any fixed
(and in fact one can be as small as
for some absolute constant
).
Now we consider the case of (7), which counts four-term progressions. Here, it turns out that Fourier-pseudorandomness is insufficient; it is possible for the quantity (7) to be significantly larger or smaller than
even if
is pseudorandom, as was observed by Gowers (with a closely related observation in the context of ergodic theory by Furstenberg).
Exercise 4 Let
be an irrational real number, let
, and let
. Show that
is Fourier-pseudorandom (keeping
and
fixed and letting
). Hint: One can use Exercise 21 from Notes 1 to show that sums of the form
cannot be large.
Exercise 5 Continuing the previous exercise, show that the expression (7) for
is equal to
as
, for some absolute constant
, if
is sufficiently small. (Hint: first show, using the machinery in Notes 1, that the two-dimensional sequence
is asymptotically equidistributed in the torus
.)
The above exercises show that a Fourier-pseudorandom set can have a four-term progression count (7) significantly larger than . One can also make the count significantly smaller than
(another observation of Gowers), but this requires more work.
Exercise 6 Let
. Show that there exists a function
with
for all
, such that the expression
is strictly less than
, where
is the subspace of quadruplets
such that
is in arithmetic progression (i.e.
for some
) and the
obey the constraint
Hint: Take
of the form
where
is a small number, and
are carefully chosen to make the
term in (8) negative.
Exercise 7 Show that there exists an absolute constant
such that for all sufficiently small
and sufficiently large
(depending on
) and a set
with
, such that (7) with
is less than
. (Hint: take
for some
, and let
be a random subset of
with each element
of
lying in
with an independent probability of
where
is the function in the previous exercise (with
), and
are real numbers which are linearly independent over
modulo
.)
For further discussion of this topic, see these slides of Wolf.
— 2. The case —
Now we consider the question of counting more general linear (or affine) patterns than arithmetic progressions. A reasonably general setting is to count patterns of the form
in a subset of a finite abelian group
(e.g. a cyclic group
), where
, and the
are affine-linear forms
for some fixed integers and group elements
. To avoid degeneracies, we will assume that all the
are surjective (or equivalently, that the
do not have a common factor that divides the order of
). This count would then be given by
where is the
-linear form
For instance, the task of counting arithmetic progressions corresponds to the case
, and
.
where
Remark 1 One can replace the
norm on
in (9) with an
norm for various values of
. The set of all admissible
is described by the Brascamp-Lieb inequality, see this paper for further discussion. We will not need these variants of (9).
Improving this trivial bound turns out to be a key step in the theory of counting general linear patterns. In particular, it turns out that for any , one usually has
except when take a very special form (or at least correlate with functions of a very special form, such as linear or higher order characters).
To reiterate: the key to the subject is to understand the inverse problem of characterising those functions for which one has
This problem is of most interest (and the most difficult) in the “ world” when
is small (e.g.
), but it is also instructive to consider the simpler cases of the “
world” when
is very close to one (e.g.
), or the “
world” when
is exactly equal to one. In these model cases one can use additional techniques (error-correction and similar techniques (often of a theoretical computer science flavour) in the
world, or exact algebraic manipulation in the
world) to understand this expression.
Let us thus begin with analysing the situation. Specifically, we assume that we are given functions
with
and wish to classify the functions as best we can. We will normalise all the norms on the right-hand side to be one, thus
for all
and
, and
By the triangle inequality, we conclude that
On the other hand, we have the crude bound
Thus equality occurs, which (by the surjectivity hypothesis on all the ) shows that
for all
and
. Thus we may write
for some phase functions
. We then have
and so from (10) one has the equation
for all and some constant
.
So the problem now reduces to the algebraic problem of solving functional equations such as (11). To illustrate this type of problem, let us consider a simple case when and
in which case we are trying to understand solutions to the functional equation
This equation involves three unknown functions . But we can eliminate two of the functions by taking discrete derivatives. To motivate this idea, let us temporarily assume that
is the real line
rather than a finite group, and that the functions
are smooth. If we then apply the partial derivative operator
to the above functional equation, one eliminates
and obtains
applying then eliminates
and leaves us with
thus vanishes identically; we can integrate this twice to conclude that
is a linear function of its input,
for some constants . A similar argument (using the partial derivative operator
to eliminate
, or by applying change of variables such as
) shows that
and
for some additional constants
. Finally, by returning to (12) and comparing coefficients we obtain the additional compatibility condition
, which one then easily verifies to completely describe all possible solutions to this equation in the case of smooth functions on
.
Returning now to the discrete world, we mimic the continuous operation of a partial derivative by introducing difference operators
for . If we difference (12) in the
variable by an arbitrary shift
by replacing
by
and then subtracting, we eliminate
and obtain
if we then difference in the variable by a second arbitrary shift
, one obtains
for all ; in particular,
for all
. Such functions are affine-linear:
Exercise 8 Let
be a function. Show that
if and only if one has
for some
and some homomorphism
. Conclude that the solutions to (12) are given by the form
, where
and
are homomorphisms with
.
Having solved the functional equation (12), let us now look at an equation related to four term arithmetic progressions, namely
for all , some constant
, and some functions
. We will try to isolate
by using discrete derivatives as before to eliminate the other functions. Firstly, we differentiate in the
direction by an arbitrary shift
, leading to
In preparation for then eliminating , we shift
backwards by
, obtaining
Differentiating in the direction by another arbitrary shift
, we obtain
We shift backwards by
again:
One final differentiation in by an arbitrary shift
gives
For simplicity, we now make the assumption that the order of
is not divisible by either
or
, so that the homomorphisms
and
are automorphisms of
. We conclude that
for all . Such functions will be called quadratic functions from
to
, thus
is quadratic. A similar argument shows that
are quadratic.
Just as (affine-)linear functions can be completely described in terms of homomorphisms, quadratic functions can be described in terms of bilinear forms, as long as one avoids the characteristic case:
Exercise 9 Let
be a finite abelian group with
not divisible by
. Show that a map
is quadratic if and only one has a representation of the form
where
,
is a homomorphism, and
is a symmetric bihomomorphism (i.e.
, and
is a homomorphism in each of
individually (holding the other variable fixed)). (Hint: Heuristically, one should set
, but there is a difficulty because the operation of dividing by
is not well-defined on
. It is, however, well-defined on
roots of unity, thanks to
not being divisible by two. Once
has been constructed, subtract it off and use Exercise 8.) What goes wrong when
is divisible by
?
Exercise 10 Show that when
is not divisible by
, that the complete solution to (13) is given by
for
,
, homomorphisms
, and symmetric bihomomorphisms
with
and
.
Exercise 11 Obtain a complete solution to the functional equation (13) in the case when
is allowed to be divisible by
or
. (This is an open-ended and surprisingly tricky exercise; it of course depends on what one is willing to call a “solution” to the problem. Use your own judgement.)
Exercise 12 Call a map
a polynomial of degree
if one has
for all
. Show that if
and
obey the functional equation
and
is not divisible by any integer between
and
, then
are polynomials of degree
.
We are now ready to turn to the general case of solving equations of the form (11). We relied on two main tricks to solve these equations: differentiation, and change of variables. When solving an equation such as (13), we alternated these two tricks in turn. To handle the general case, it is more convenient to rearrange the argument by doing all the change of variables in advance. For instance, another way to solve (13) is to first make the (non-injective) change of variables
for arbitrary , so that
and (13) becomes
for all . The point of performing this change of variables is that while the
term (for instance) involves all the three variables
, the remaining terms only depend on two of the
at a time. If we now pick
arbitrarily, and then differentiate in the
variables by the shifts
respectively, then we eliminate the
terms and arrive at
which soon places us back at (14) (assuming as before that is not divisible by
or
).
Now we can do the general case, once we put in place a definition (from this paper of mine with Ben Green):
Definition 1 (Cauchy-Schwarz complexity) A system
of affine-linear forms (with linear coefficients in
) have Cauchy-Schwarz complexity at most
if, for every
, one can partition
into
classes (some of which may be empty), such that
does not lie in the affine-linear span (over
) of the forms in any of these classes. The Cauchy-Schwarz complexity of a system is defined to be the least such
with this property, or
if no such
exists.
The adjective “Cauchy-Schwarz” (introduced by Gowers and Wolf) may be puzzling at present, but will be motivated later.
This is a somewhat strange definition to come to grips with at first, so we illustrate it with some examples. The system of forms is of complexity
; given any form here, such as
, one can partition the remaining forms into two classes, namely
and
, such that
is not in the affine-linear span of either. On the other hand, as
is in the affine linear span of
, the Cauchy-Schwarz complexity is not zero.
Exercise 13 Show that for any
, the system of forms
has complexity
.
Exercise 14 Show that a system of non-constant forms has finite Cauchy-Schwarz complexity if and only if no form is an affine-linear combination of another.
There is an equivalent way to formulate the notion of Cauchy-Schwarz complexity, in the spirit of the change of variables mentioned earlier. Define the characteristic of a finite abelian group to be the least order of a non-identity element.
Proposition 2 (Equivalent formulation of Cauchy-Schwarz complexity) Let
be a system of affine-linear forms. Suppose that the characteristic of
is sufficiently large depending on the coefficients of
. Then
has Cauchy-Schwarz complexity at most
if and only if, for each
, one can find a linear change of variables
over
such that the form
has non-zero
coefficients, but all the other forms
with
have at least one vanishing
coefficient, and
is the linear form induced by the integer coefficients of
.
Proof: To show the “only if” part, observe that if and
is as above, then we can partition the
,
into
classes depending on which
coefficient vanishes for
(breaking ties arbitrarily), and then
is not representable as an affine-linear combination of the forms from any of these classes (here we use the large characteristic hypothesis). Conversely, suppose
has Cauchy-Schwarz complexity at most
, and let
. We can then partition the
into
classes
, such that
cannot be expressed as an affine-linear combination of the
from
for any
. By duality, one can then find vectors
for each
such that
does not annihilate
, but all the
from
do. If we then set
then we obtain the claim.
Exercise 15 Let
be a system of affine-linear forms with Cauchy-Schwarz complexity at most
, and suppose that the equation (11) holds for some finite abelian group
and some
. Suppose also that the characteristic of
is sufficiently large depending on the coefficients of
. Conclude that all of the
are polynomials of degree
.
It turns out that this result is not quite best possible. Define the true complexity of a system of affine-linear forms to be the largest
such that the powers
are linearly independent over
.
Exercise 16 Show that the true complexity is always less than or equal to the Cauchy-Schwarz complexity, and give an example to show that strict inequality can occur. Also, show that the true complexity is finite if and only if the Cauchy-Schwarz complexity is finite.
Exercise 17 Show that Exercise 15 continues to hold if Cauchy-Schwarz complexity is replaced by true complexity. (Hint: first understand the cyclic case
, and use Exercise 15 to reduce to the case when all the
are polynomials of bounded degree. The main point is to use a “Lefschetz principle” to lift statements in
to a characteristic zero field such as
.) Show that the true complexity cannot be replaced by any smaller quantity.
See this paper of Gowers and Wolf for further discussion of the relationship between Cauchy-Schwarz complexity and true complexity.
— 3. The Gowers uniformity norms —
In the previous section, we saw that equality in the trivial inequality (9) only occurred when the functions were of the form
for some polynomials
of degree at most
, where
was the true complexity (or Cauchy-Schwarz complexity) of the system
. Another way of phrasing this latter fact is that one has the identity
for all , where
is the multiplicative derivative
This phenomenon extends beyond the “ world” of exact equalities. For any
and
, we define the Gowers norm
by the formula
note that this is equivalent to (6). Using the identity
we easily verify that the expectation in the definition of (16) is a non-negative real. We also have the recursive formula
for all .
The norm essentially just the mean:
As such, it is actually a seminorm rather than a norm.
The norm can be computed in terms of the Fourier transform:
Exercise 18 (Fourier representation of
) Define the Pontryagin dual
of a finite abelian group
to be the space of all homomorphisms
. For each function
, define the Fourier transform
by the formula
. Establish the identity
In particular, the norm is a genuine norm (thanks to the norm properties of
, and the injectivity of the Fourier transform).
For the higher Gowers norms, there is not nearly as nice a formula known in terms of things like the Fourier transform, and it is not immediately obvious that these are indeed norms. But this can be established by introducing the more general Gowers inner product
for any -tuple
of functions
, thus in particular
The relationship between the Gowers inner product and the Gowers uniformity norm is analogous to that between a Hilbert space inner product and the Hilbert space norm. In particular, we have the following analogue of the Cauchy-Schwarz inequality:
Exercise 19 (Cauchy-Schwarz-Gowers inequality) For any tuple
of functions
, use the Cauchy-Schwarz inequality to show that
for all
, where for
and
,
is formed from
by replacing the
coordinate with
. Iterate this to conclude that
Then use this to conclude the monotonicity formula
for all
, and the triangle inequality
for all
. (Hint: For the latter inequality, raise both sides to the power
and expand the left-hand side.) Conclude in particular that the
norms are indeed norms for all
.
The Gowers uniformity norms can be viewed as a quantitative measure of how well a given function behaves like a polynomial. One piece of evidence in this direction is:
Exercise 20 (Inverse conjecture for the Gowers norm,
case) Let
be such that
, and let
. Show that
, with equality if and only if
for some polynomial
of degree at most
.
The problem of classifying smaller values of is significantly more difficult, and will be discussed in later notes.
Exercise 21 (Polynomial phase invariance) If
is a function and
is a polynomial of degree at most
, show that
. Conclude in particular that
where
ranges over polynomials of degree at most
.
The main utility for the Gowers norms in this subject comes from the fact that they control many other expressions of interest. Here is a basic example:
Exercise 22 Let
be a function, and for each
, let
be a function bounded in magnitude by
which is independent of the
coordinate of
. Let
be non-zero integers, and suppose that the characteristic of
exceeds the magnitude of any of the
. Show that
Hint: induct on
and use (17) and the Cauchy-Schwarz inequality.
This gives us an analogue of Exercise 15:
Exercise 23 (Generalised von Neumann inequality) Let
be a collection of affine-linear forms
with Cauchy-Schwarz complexity
. If the characteristic of
is sufficiently large depending on the linear coefficients of
, show that one has the bound
whenever
are bounded in magnitude by one.
Conclude in particular that if
is a subset of
with
, then
From the above inequality, we see that if has some positive density
but has much fewer than
(say) patterns of the form
with
, then we have
This is the initial motivation for studying inverse theorems for the Gowers norms, which give necessary conditions for a (bounded) function to have large norm. This will be a focus of subsequent notes.

30 comments
Comments feed for this article
27 April, 2010 at 11:24 am
mfrasca
Hi Terry,
There seem to be a lot of “Formula does not parse” messages. Is it just my problem?
Marco
28 April, 2010 at 2:29 pm
Joel Moreira
Dear Prof. Tao
In Exercise 3, I think something is missing, since q isn’t used (and the hint doesn’t seem to make sense)
28 April, 2010 at 2:43 pm
Terence Tao
Ah, there was a “mod q” missing in one of the displays. Thanks for the correction!
28 April, 2010 at 2:02 pm
jc
Not sure if this is the right place to post this, but I was browsing arxiv trackbacks and noticed that for your posts that link arxiv articles, in addition to the trackbacks expected, wordpress is also sending trackbacks for Thurston’s article linked in the sidebar.
See e.g. http://arxiv.org/tb/math/9404236
29 April, 2010 at 12:28 pm
Ryan
Does anyone else find that these 254B lecture notes posts do not show up in the RSS feed, or is it just me?
8 May, 2010 at 1:48 pm
254B, Lecture Notes 4: Equidistribution of polynomials over finite fields « What’s new
[…] from the previous notes that a function is a function is a polynomial of degree at most […]
19 May, 2010 at 11:38 pm
Pietro
Dear Terry,
in your definition of the Gowers inner product, I think you want to take the expectation over x,h_1,…,h_d of the expression that you have.
Thanks for the great notes and blog!
20 May, 2010 at 2:02 pm
Pietro
Also, in exercise 1, I guess we want the intersection of A and A+h to have size >> delta squared times N.
20 May, 2010 at 3:35 pm
Terence Tao
Thanks for the corrections!
20 May, 2010 at 9:44 pm
254B, Notes 5: The inverse conjecture for the Gowers norm I. The finite field case « What’s new
[…] regularity lemma, Gowers uniformity norms, polynomials, Szemeredi's theorem | by Terence Tao In Notes 3, we saw that the number of additive patterns in a given set was (in principle, at least) controlled […]
5 June, 2010 at 12:58 pm
254B, Lecture Notes 7: The transference principle, and linear equations in primes « What’s new
[…] will rely solely on the Cauchy-Schwarz inequality, using a weighted version of the arguments from Notes 3 that first appeared in this paper of Green and myself. We wish to control the […]
11 December, 2012 at 9:04 pm
Mixing for progressions in non-abelian groups « What’s new
[…] arguments let one conclude that are affine homomorphisms; see e.g. Section 2 of these lecture notes. It turns out that essentially the same argument can be applied in the nonabelian case, but one […]
30 March, 2013 at 4:27 am
Rex
Dear Terry,
There seems to be a discrepancy between the definition of the Gowers norm in “The primes contain arbitrarily long arithmetic progressions”:
versus the one used in the later “Linear equations” series:
Namely, the alternating conjugation is missing. Is there any particular reason for this change?
Of course, there is no difference when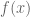 is real-valued, but “The primes contain…” remarks in the section on anti-uniformity that:
is real-valued, but “The primes contain…” remarks in the section on anti-uniformity that:
Given a polynomial of degree
of degree  , we have
, we have  , where
, where  . This comes from the fact that taking
. This comes from the fact that taking 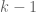 successive differences of
successive differences of 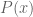 gives the zero function.
gives the zero function.
For this example to work, it seems that we need the conjugation to be present.
30 March, 2013 at 7:48 am
Terence Tao
See Footnote 14 in the most recent version http://arxiv.org/abs/math/0404188 of the “The primes contain…” paper.
20 July, 2015 at 8:23 pm
A nonstandard analysis proof of Szemeredi’s theorem | What's new
[…] in numerous places in the literature (e.g. Lemma 11.4 of my book with Van Vu, or Exercise 23 of this blog post) and will not be repeated here. In particular, from multilinearity we see […]
14 August, 2018 at 6:12 am
farlabb
Dear professor Tao,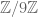 , which has characteristic 3. For
, which has characteristic 3. For  , take $a=2$ and the statement then is
, take $a=2$ and the statement then is  . But in this case one can just take a function which is nonzero on
. But in this case one can just take a function which is nonzero on  but 0 on the rest.
but 0 on the rest.
I am having struggles proving exercise 22. It seems as if I have found a counterexample. I looked at the group
I am also a little bit confused about your definition of affine linear form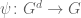 . You define it to be maps of the form
. You define it to be maps of the form  for integers
for integers 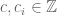 , but in a group, what does
, but in a group, what does 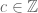 mean? If
mean? If  were a ring with unit, I would understand.
were a ring with unit, I would understand.
Thanks a lot in advance!
14 August, 2018 at 6:14 am
farlabb
Please ignore my first question (about counterexample as it is not correct what I wrote).
14 August, 2018 at 6:27 am
Terence Tao
Abelian groups are canonically modules over the integers, e.g.,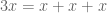 and
and  .
.
14 August, 2018 at 6:33 am
farlabb
Thanks for the reply. I understand it if you write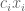 where
where  and
and  , but how do I interpret
, but how do I interpret  as an element of
as an element of  ? Because in the definition of
? Because in the definition of  we write
we write 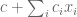 .
.
14 August, 2018 at 6:34 am
farlabb
Sorry for the typo, and
and 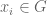 .
.
15 August, 2018 at 7:42 am
Terence Tao
This is a typo: should be an element of
should be an element of  , not of
, not of  . I will amend the text accordingly.
. I will amend the text accordingly.
24 August, 2018 at 5:02 am
iPie
Hi prof. Tao, I find the proof of proposition 2 (equivalent formulation of CS-complexity) hard to follow (it could be me of course). I don’t understand how you use the large characteristic hypothesis to proof the “only if” part. Could you please explain it in more detail?
24 August, 2018 at 8:14 am
Terence Tao
Fix . By hypothesis, the rational form
. By hypothesis, the rational form 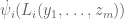 has non-vanishing
has non-vanishing  coefficient. If the characteristic is large enough that it does not divide the numerator of this coefficient, this implies that the G-form
coefficient. If the characteristic is large enough that it does not divide the numerator of this coefficient, this implies that the G-form  also has non-vanishing coefficient. On the other hand, all the forms
also has non-vanishing coefficient. On the other hand, all the forms  in the class associated to
in the class associated to  have vanishing
have vanishing  coefficient. Hence
coefficient. Hence  cannot be an affine-linear combination of these
cannot be an affine-linear combination of these  .
.
7 June, 2020 at 6:06 am
Rok H.
Dear Professor Tao,
in the Exercise 8, it should be $a_1 = a_2 = – a_3$.
[Corrected, thanks – T.]
19 August, 2021 at 10:27 pm
Anonymous
I have a question about Exercise 5:
Set
 .
.
By equidistribution, it looks like
![|\{ (n,r) \in [N]^2 : (n,n-r,n-2r,n-3r) \in A \}| = ( N^2 + o_{N \to \infty}(1) ) \cdot \int_{y \cdot k_0= 0} \mathbf{1}_A(y) \ dy](https://s0.wp.com/latex.php?latex=%7C%5C%7B+%28n%2Cr%29+%5Cin+%5BN%5D%5E2+%3A+%28n%2Cn-r%2Cn-2r%2Cn-3r%29+%5Cin+A+%5C%7D%7C+%3D+%28+N%5E2+%2B+o_%7BN+%5Cto+%5Cinfty%7D%281%29+%29+%5Ccdot+%5Cint_%7By+%5Ccdot+k_0%3D+0%7D+%5Cmathbf%7B1%7D_A%28y%29+%5C+dy&bg=ffffff&fg=545454&s=0&c=20201002)
where
I’m getting a little confused because it looks to me like
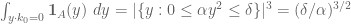 ,
,
which differs from the desired bound.
bound.
20 August, 2021 at 5:37 am
Terence Tao
The set you write is not well defined (if
you write is not well defined (if  , then
, then  is not well-defined). You may be thinking of
is not well-defined). You may be thinking of  instead. In this case, the indicator function
instead. In this case, the indicator function 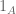 in your expression should be replaced by
in your expression should be replaced by ![1_{[0,\delta]^4}](https://s0.wp.com/latex.php?latex=1_%7B%5B0%2C%5Cdelta%5D%5E4%7D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
21 August, 2021 at 2:20 am
Anonymous
Thanks a lot!
13 November, 2021 at 3:49 am
Killua Zoldyck
Dear Prof. Tao, shouldn’t it be
shouldn’t it be  as the
as the 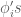 are taking values in
are taking values in  .
.
In the statement below equation labelled
[Corrected, thanks – T.]
6 January, 2022 at 1:31 am
Killua Zoldyck
@Anonymous and @farlabb can we please connect via email at lucifer3099@gmail.com as i wanted to discuss some of the exercises.
28 January, 2022 at 6:09 am
Anonymous
Dear Prof Tao,
Can you please provide me with an hint on how to approach the exercise 4 in this section using the exercise 21 in section 1 (like explain how to work with the given hint) ? It is not very clear to me how to make use of exercise 21 in section 1.
[Approximate the cutoff![1_{[0,\delta]}( x \hbox{ mod } 1)](https://s0.wp.com/latex.php?latex=1_%7B%5B0%2C%5Cdelta%5D%7D%28+x+%5Chbox%7B+mod+%7D+1%29&bg=ffffff&fg=545454&s=0&c=20201002) by a trigonometric polynomial, so that the indicator function of
by a trigonometric polynomial, so that the indicator function of  can be approximated by a finite linear combination of functions of the forn
can be approximated by a finite linear combination of functions of the forn  . -T]
. -T]