Szemerédi’s theorem asserts that any subset of the integers of positive upper density contains arbitrarily large arithmetic progressions. Here is an equivalent quantitative form of this theorem:
Theorem 1 (Szemerédi’s theorem) Let
be a positive integer, and let
be a function with
for some
, where we use the averaging notation
,
, etc.. Then for
we have
for some
depending only on
.
The equivalence is basically thanks to an averaging argument of Varnavides; see for instance Chapter 11 of my book with Van Vu or this previous blog post for a discussion. We have removed the cases as they are trivial and somewhat degenerate.
There are now many proofs of this theorem. Some time ago, I took an ergodic-theoretic proof of Furstenberg and converted it to a purely finitary proof of the theorem. The argument used some simplifying innovations that had been developed since the original work of Furstenberg (in particular, deployment of the Gowers uniformity norms, as well as a “dual” norm that I called the uniformly almost periodic norm, and an emphasis on van der Waerden’s theorem for handling the “compact extension” component of the argument). But the proof was still quite messy. However, as discussed in this previous blog post, messy finitary proofs can often be cleaned up using nonstandard analysis. Thus, there should be a nonstandard version of the Furstenberg ergodic theory argument that is relatively clean. I decided (after some encouragement from Ben Green and Isaac Goldbring) to write down most of the details of this argument in this blog post, though for sake of brevity I will skim rather quickly over arguments that were already discussed at length in other blog posts. In particular, I will presume familiarity with nonstandard analysis (in particular, the notion of a standard part of a bounded real number, and the Loeb measure construction), see for instance this previous blog post for a discussion.
By routine “compactness and contradiction” arguments (as discussed in this previous post), Theorem 1 can be deduced from the following nonstandard variant:
Theorem 2 Let
be a nonstandard positive integer, let
be the nonstandard cyclic group
, and let
be an internal function with
. Then for any standard
,
Here of course the averaging notation is interpreted internally.
Indeed, if Theorem 1 failed, one could create a sequence of functions of density at least
for some fixed
, and a fixed
such that
taking ultralimits one can then soon obtain a counterexample to Theorem 2.
It remains to prove Theorem 2. Henceforth is a fixed nonstandard positive integer, and
. By the Loeb measure construction (discussed in this previous blog post), one can give
the structure of a probability space
(the Loeb space of
), such that every internal subset
of
is (Loeb) measurable with
which implies that any bounded internal function has standard part
which is (Loeb) measurable with
Conversely, a countable saturation argument shows that any function in is equal almost everywhere to the standard part of a bounded internal function.
From Hölder’s inequality we see that the -linear form
vanishes if one of the has standard part vanishing almost everywhere. As such, we can (by abuse of notation) extend this
-linear form to functions
that are elements of
, rather than bounded internal functions. With this convention, we see that Theorem 2 is equivalent to the following assertion.
Theorem 3 For any non-negative
with
, one has for any standard
,
The next step is to introduce the Gowers-Host-Kra uniformity seminorms , defined for
by the formula
where is any bounded internal function whose standard part equals
almost everywhere. From Hölder’s inequality one can see that the exact choice of
does not matter, so that this seminorm is well-defined. (It is indeed a seminorm, but we will not need this fact here.)
We have the following application of the van der Corput inequality:
Theorem 4 (Generalised von Neumann theorem) Let
be standard. For any
with
for some
, one has
This estimate is proven in numerous places in the literature (e.g. Lemma 11.4 of my book with Van Vu, or Exercise 23 of this blog post) and will not be repeated here. In particular, from multilinearity we see that
whenever with
.
Dual to the Gowers norms are the uniformly almost periodic norms
. Let us first define the internal version of these norms. We define
to be the space of constant internal functions
, with internal norm
. Once
is defined for some
, we define
to be the internal normed vector space of internal functions
for which there exists a nonstandard real number
, an internally finite non-empty set
, an internal family
of internal functions
bounded in magnitude by one for each
, and an internal family
of internal functions
in the unit ball of
such that one had the representation
for all , where
is the shift of
by
. The internal infimum of all such
is then the
norm of
. This gives each of the
the structure of an internal shift-invariant Banach algebra; see Section 5 of . The
norms also controlled the supremum norm:
In particular, if we write for the space of standard parts of internal functions of bounded norm in
, then
is an (external) Banach algebra contained (as a real vector space) in
. For
, we can then define a factor
of
to be the probability space
, where
is the subalgebra of
consisting of those sets
such that
lies in the
closure of
. This is easily seen to be a shift-invariant
-algebra, and so
is a factor.
We have the following key characteristic factor relationship:
Theorem 5 Let
with
. Then
.
In fact the converse implication is true also (making the universal characteristic factor for the
seminorm), but we will not need this direction of the implication.
Proof: Suppose for contradiction that ; we can normalise
. Writing
for some bounded internal
, we then see that
has a non-zero inner product with
, where the dual function
for
is the bounded internal function
From the easily verified identity
and a routine induction, we see that lies in the unit ball of
, and so
is measurable with respect to
. By hypothesis this implies that
is orthogonal to
, a contradiction.
In view of the above theorem and (1), we may replace by
without affecting the average in Theorem 3. Thus that theorem is equivalent to the following.
Theorem 6 Let
and
be standard. Then for any non-negative
with
, one has
We only apply this theorem in the case and
, but for inductive purposes it is convenient to decouple the two parameters.
We prove Theorem 6 by induction on (allowing
to be arbitrary). When
, the claim is obvious for any
because all functions in
are essentially constant. Now suppose that
and that the claim has already been proven for
.
Let be a nonnegative function whose mean
is positive; we may normalise
to take values in
. Let
be standard, and let
be a sufficiently small standard quantity depending on
to be chosen later (one could for instance take
, but we will not attempt to optimise in
). As
is
-measurable, one can find an internal function
with
and bounded
norm such that
. (Note though that while the
norm of
is bounded, this bound could be extremely large compared to
,
,
.)
Set . We define the relative inner product
for
by the formula
and the relative norm
This gives the structure of a (pre-)Hilbert module over
, as discussed in this previous blog post.
A crucial point is that the function is relatively almost periodic over the previous characteristic factor
, in the following sense.
Proposition 7 (Relative almost periodicity) There exists a standard natural number
and functions
in the unit ball of
with the following “relative total boundedness” property: for any
, there exists a
-measurable function
such that
almost everywhere (where
is short-hand for
).
Proof: This will be a relative version of the standard analysis fact that integral operators on finite measure spaces with bounded kernel are in the Hilbert-Schmidt class, and thus compact.
By construction, there exists an internally finite non-empty set , an internal collection
of internal functions
that are uniformly bounded in
, and an internal collection
of internal functions
that are uniformly bounded in
, such that
for all . Note in particular that the
all lie in a bounded subset of
, and the
all lie in a bounded subset of
.
We give the
-algebra generated from the standard parts of bounded internal functions
such that the standard parts of
all lie in a bounded subset of
; this gives a probability space that extends the product measure of
and
. We define an operator
as follows. If
, then
is the standard part of some bounded internal function
. We then define
by the formula
This can easily be seen to not depend on the choice of , and
defines a
-linear operator (embedding
into both
and
in the obvious fashion). Note that
lies in the range of
applied to a function in the unit ball of
.
Now we claim that this operator is relatively Hilbert-Schmidt over , in the sense that there exists a finite bound
such that
for all finite collections of functions that are relatively orthonormal over
in the sense that
and
for all and
. Indeed, the left-hand side of (4) may be expanded first as
for some sequence in
with
, and then as
where we use Loeb measure on and
is the function
, and
are lifted up to
in the obvious fashion. By Cauchy-Schwarz and the boundedness of
, we can bound this by
But the are relatively orthonormal over
(this reflects the relative orthogonality of
and
over
), so that
and the claim follows from the hypotheses on .
Using the relative spectral theorem for relative Hilbert-Schmidt operators (see Corollary 17 of this blog post), we may thus find relatively orthonormal systems in
and
respectively over
and a non-increasing sequence of non-negative coefficients
(the relative singular values) with
almost everywhere, such that we have the spectral decomposition
wiht the sum converging in . (If
were standard Borel spaces, one could deduce this theorem from the usual spectral theorem for Hilbert-Schmidt operators using disintegration. Loeb spaces are certainly not standard Borel, but as discussed in the linked blog post above, one can adapt the proof of the spectral theorem to the relative setting without using the device of disintegration.
Since and the
are decreasing, one can find an
such that
almost everywhere for all
. For
in the unit ball of
, this lets one approximate
by the finite rank operator
to within
almost everywhere in
norm. If one rounds
to the nearest multiple of
for each
, and lets
be the collection of linear combinations of the form
with
a multiple of
, we obtain the claim.
We return to the proof of (2). Since and
, we have
if is small enough. In particular there is a
-measurable set
of measure at least
such that
on
. Since
we see from Markov’s inequality (for small enough ) that there is a
-measurable subset
of
of measure at least
such that
on , where we write
for the relative norm. In particular we have
almost everywhere on .
Let be a sufficiently large standard natural number (depending on
and the quantity
from Proposition 7), in fact it will essentially be a van der Waerden number of these inputs) to be chosen later. Applying the induction hypothesis, we have
In particular, there is a standard , such that for
in a subset of
of measure at least
, we have
or equivalently that the set
has measure at least .
Let be as above, and let
be the functions from Proposition 7. Then for
, we can find a measurable function
such that
almost everywhere on , hence by (5) we have
almost everywhere on . From this and the relative Hölder inequality, we see that
a.e. on whenever
.
Now, for large enough, we see from van der Warden’s theorem that there exist measurable
such that
almost everywhere in , and hence in
(this can be seen by partitioning
into finitely many pieces, with each of the
constant on each of these pieces). For that choice of
we have
and
and thus
almost everywhere on . But from (6) one has
a.e. on , so from Hölder’s inequality we have (for
sufficiently small) that
From non-negativity of , this implies that
which on integrating in gives
Averaging in , we conclude that
Shifting by
, we conclude that
Dilating by
(and noting that the map
is at most
-to-one on
), we conclude that
and (2) follows.

32 comments
Comments feed for this article
21 July, 2015 at 7:24 am
Mikhail Katz
Your notation in theorem 1 for the expected value over x, r is a bit ambiguous. I assume the average is still over x rather than r.
[Clarification added – T.]
21 July, 2015 at 7:29 pm
William Gasarch
What is the easiest proof of Sz theorem known? Is it the one in this blog, or the elementary proof of DHJ, or something else? I know this depends on your definition of easy, so I admit I am asking for a discussion of the point.
22 July, 2015 at 1:34 pm
Terence Tao
My personal favorite is the proof using the hypergraph removal lemma, which nowadays has a reasonably simple (and elementary) proof, but the Furstenberg proof (which is not too far in spirit from the one given here) and the Polymath1 proof of density Hales-Jewett are certainly also quite simple and conceptual (though the Furstenberg proof would not be considered elementary, as for instance it uses measure theory and the spectral theorem). I suppose if one had to cover Szemeredi’s theorem (and ONLY this theorem) in as few lectures as possible to a class of beginning graduate students, the Polymath1 proof would be the fastest, though the other proofs are instructive in a number of other ways that would be useful beyond the narrow goal of proving Szemeredi’s theorem, and so there would be pedagogical advantages with using those proofs instead.
22 July, 2015 at 12:29 pm
Miklos Abert
I am confused. Can you clarify in what way this is significantly different from Balazs Szegedy’s approach to HOF? I am assuming you know his work.
22 July, 2015 at 12:36 pm
Terence Tao
They are similar in that they both use the Gowers norms and nonstandard analysis, but Szegedy’s approach is closer to Host-Kra’s work on characteristic factors and to my work with Green and Ziegler on the inverse conjecture for the Gowers norms, whereas the argument here is closer to the original arguments of Furstenberg (and Furstenberg-Katznelson-Ornstein) proving Szemeredi’s theorem. At a more technical level, the analysis here only uses the relatively easy fact that the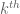 Host-Kra factor is a compact extension of the
Host-Kra factor is a compact extension of the  factor, whereas the analysis of Host-Kra and Szegedy requires a much finer analysis of that extension (roughly, that it is an abelian extension by a cocycle obeying a certain “type equation”, which must then be solved for, or at least (in Szegedy’s approach) used to construct a topological nilspace which one then tries to classify). These are all overkill for the purposes of just proving Szemeredi’s theorem; the arguments of Szegedy or of Host-Kra (or of the more recent work of Gutman-Manners-Varju repairing and building upon Szegedy’s work) are significantly lengthier than those provided here, though they also provide much more precise information. (To give just one example, Furstenberg’s argument shows in a dynamical system that the averages
factor, whereas the analysis of Host-Kra and Szegedy requires a much finer analysis of that extension (roughly, that it is an abelian extension by a cocycle obeying a certain “type equation”, which must then be solved for, or at least (in Szegedy’s approach) used to construct a topological nilspace which one then tries to classify). These are all overkill for the purposes of just proving Szemeredi’s theorem; the arguments of Szegedy or of Host-Kra (or of the more recent work of Gutman-Manners-Varju repairing and building upon Szegedy’s work) are significantly lengthier than those provided here, though they also provide much more precise information. (To give just one example, Furstenberg’s argument shows in a dynamical system that the averages 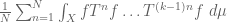 are bounded below, but not that these averages converge to a limit; this latter fact was first proven in the above-mentioned work of Host and Kra using the advanced structure theory of characteristic factors that Szegedy later found nonstandard analogues of.)
are bounded below, but not that these averages converge to a limit; this latter fact was first proven in the above-mentioned work of Host and Kra using the advanced structure theory of characteristic factors that Szegedy later found nonstandard analogues of.)
23 July, 2015 at 7:08 am
Miklos Abert
Thanks, Terry! Your response clarifies a lot, but at the same time, it confuses me even more, for two reasons – I may be wrong in both of course.
1) Your theorems and notions above seem to be mostly byproducts of Szegedy’s already published work. You yourself hint at this when you call his work an overkill for the topic of this post. Simplifying and modifying other’s proofs can of course involve high level mathematics and can be very productive. Clearly, the community will benefit from your post. What confuses me here is that you fail to mention Szegedy’s name in it.
2) You write about the very recent and unpublished work of Gutman-Manners-Varju as something repairing Szegedy’s work. That is a strong word as it suggests that there are significant errors or gaps in Szegedy’s work. Are you aware of such? If yes, can you please clarify what they are? My understanding is that while the entry cost to Szegedy’s work on HOF is quite high, no one has found a concrete significant mistake or gap in it yet. Is that wrong?
Regards,
Miklos
23 July, 2015 at 12:18 pm
Terence Tao
As stated in my post, the proof here is essentially the nonstandard analysis translation of my proof of Szemeredi’s theorem from 2004. At the time, I had not learned nonstandard analysis, which I did at around 2007; I only got around to writing down a nonstandard translation of the argument because of some recent conversations with colleagues about the possibility of doing so. (This is not the first time that nonstandard translations of combinatorial arguments have been presented in this area; for instance, in 2007, Towsner gave a nonstandard translation of an ergodic convergence result of myself from earlier that year. I think the use of nonstandard methods in ergodic theory can be traced back to the 1982 paper of Kamae giving a nonstandard proof of the ergodic theorem via the Loeb measure construction.)
Of course, from about 2009 onwards, Szegedy also started to use nonstandard methods to attack related questions, such as the inverse conjecture for the Gowers norms. However, the methods described in this blog post go back much further than that, and can be largely traced back to the 1977 paper of Furstenberg (though with some simplifications using the Gowers-Host-Kra uniformity seminorms introduced by Gowers in 2001 and Host-Kra in 2005, as well as the uniform almost periodicity norms introduced in my 2004 paper).
Regarding the issue (involving a subtle distinction between the measurable and continuous nilspace categories) with the 2010 arXiv version of the paper with Camarena, this was confirmed to me as a problem by Balazs back in Nov 2010, and it should be fixable, but I don’t know if an updated version of this paper is available (perhaps Balazs himself could comment on the latest status).
24 July, 2015 at 11:02 am
Balazs Szegedy
Let me reply to the correctness issue first.
In 2010 November, after I announced my version of the inverse theorem for the Gowers norms at the Szemeredi 70 conference, you and I had an
e-mail conversation on my paper with Camarena on nilspaces – this is the one that deals with the algebraic part of my theory. I indeed wrote you that I plan to add an extra chapter further clarifying the continuity issue related to cocycles, mainly because I wasn’t quite happy with the presentation myself. However, I never hinted at an error in the paper, because I was not aware of one. That is still the case. One can easily check on the later arxiv version (2012) that no major changes were done, just a more detailed writeup.
It is true that even the 2012 version is a very dense and abstract paper and would deserve an even more detailed exposition but up to my knowledge, no substantial mistake has been found yet. Let me spell it out: I am not aware of such mistakes and no one has contacted me about such. As with many long papers, there are a number of small mistakes and typos and weaknesses in the explanation.
Back to the issue of ultrafilters.
Of course Furstenberg was the sole major source of this line of work. However, in my opinion it was a rather non-trivial step to identify the right framework that allowed for a clean way of interpreting the classical notions of Furstenberg’s theory in higher order Fourier analysis. This framework is the ultra-product characteristic factor language that I introduced based on another non-trivial work by myself and Elek on hypergraph-regularity.
The identification of the unique characteristic factors on ultraproduct groups opened up a perspective that I could use e.g. to prove inverse theorems for the Gowers norms on arbitrary compact abelian groups. The existence of these unique sigma-algebras appear first in my H.O.F paper from 2009.
Following your logic, the hypergraph removal lemma that I proved with Elek and which follows easily from the Lebesgue density theorem in the nonstandard setting is just a translation. The problem with this point of view is, that often the real mathematical work is done exactly in these translations and the nonstandard setting requires very new ways to prove the same kind of theorem. The same phenomenon happens in HOF.
24 July, 2015 at 12:15 pm
Terence Tao
To remind you of the issue with the paper which I previously sent to you (in my email of Nov 8, 2010), using the section numbering of the 2012 version of your paper with Camarena:
In the first paragraph of Section 3.10 on Page 48, you write that “by abusing the notation” you redefine the space to denote the space of continuous translations; previously, they were simply the space of translations without continuity hypotheses. Then, at the end of the proof of Lemma 3.23, you assert that “Lemma 3.19 and Lemma 2.1 finish the proof”. However, Lemma 2.1 is stated and proved for the category of nilspaces, not of continuous nilspaces. As such, it is not clear why the object
to denote the space of continuous translations; previously, they were simply the space of translations without continuity hypotheses. Then, at the end of the proof of Lemma 3.23, you assert that “Lemma 3.19 and Lemma 2.1 finish the proof”. However, Lemma 2.1 is stated and proved for the category of nilspaces, not of continuous nilspaces. As such, it is not clear why the object 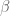 produced by Lemma 3.23 is continuous, as it ought to be to be consistent with the “abuse of notation”. Indeed, given that the section
produced by Lemma 3.23 is continuous, as it ought to be to be consistent with the “abuse of notation”. Indeed, given that the section  is merely Borel measurable rather than continuous, it is likely that the
is merely Borel measurable rather than continuous, it is likely that the 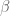 produced by this argument is also only measurable instead of continuous. It does appear that you have added a result (Theorem 2) in the 2012 version that may help address this issue, but at a bare minimum one needs a version of Lemma 2.1 in the measurable category.
produced by this argument is also only measurable instead of continuous. It does appear that you have added a result (Theorem 2) in the 2012 version that may help address this issue, but at a bare minimum one needs a version of Lemma 2.1 in the measurable category.
Regarding the ultraproduct setting, it is true that you were one of the first authors to clean up combinatorial arguments of Szemeredi type by working in the nonstandard setting, starting with your 2007 paper with Elek and then your later 2009 papers on higher order Fourier analysis. But there was parallel work by other authors; see for instance this 2007 paper by Towsner translating a combinatorial argument of my own into the nonstandard setting. In 2009, Ben Green, Tamar Ziegler and I gave a combinatorial proof of the U^4 inverse theorem, and announced that the inverse theorem for higher U^k norms (which appeared in 2010) would use nonstandard analysis (see page 2 of the U^4 paper).
Without nonstandard analysis, the arguments are significantly less clean, but still doable. For instance the combinatorial analogue of characteristic factors was first introduced in my 2004 paper with Ben Green (see Footnote 8), then developed further in another 2004 paper of mine (see Remark 3.7). These combinatorial characteristic factors are not mere “analogues” of their nonstandard counterparts; they are logically equivalent through the transfer principle (roughly speaking, the nonstandard characteristic factor is generated by ultralimits of functions in the combinatorial characteristic factor). Similarly for the combinatorial and nonstandard versions of relative almost periodicity, the former of which appears in my 2004 paper, and the latter of which appears here and (essentially) in your HOF paper (although your formulation does not explicitly use the UAP norms that were one of the innovations of my 2004 paper, and which I continue to use in this blog post).
Your HOF paper did show that much of the Host-Kra machinery (e.g. the Furstenberg-Weiss reduction to abelian extensions and the Host-Kra type equation for cocycles, and the appearance of Host-Kra strong parallelepiped structures (which you call nilspaces)) could be extended to the nonstandard setting, and thus in principle to the combinatorial setting, and this had not been previously done in the literature. However, this machinery is not needed for the narrow goal of proving Szemeredi’s theorem, which is the focus of this blog post (and of the 2004 paper that it is based on).
23 July, 2015 at 9:53 am
Balazs Szegedy
Hi Terry, following earlier comments I think I have a clarifying question here about this post.
The main idea in my approach to Higher Order Fourier analysis was to carry out the following program 1) Take the ultra product of finite abelian groups 2) Identify the characteristic factors for the Gowers (and Host-Kra) semi-norms 3) Give a number of equivalent but increasingly stronger descriptions for these characteristic factors leading to a structure theorem.
The cocycle theorem that you mention in your reply to Abert is one of these equivalent characterisations (of intermediate difficulty) however I have a number of easier ones expressing relative compactness. For example I prove that if you take the sigma algebra F_k and the Hilbert space of L^2 functions in it then it is linearly generated by finite rank shift invariant modules over the algebra of L^\infty functions in F_{k-1}. The proof of this is tricky but not hard. My main question is: Is this equivalent with your “Relative almost periodicity” or maybe I misunderstand something.
Balazs
23 July, 2015 at 12:06 pm
Terence Tao
Yes, relative almost periodicity (in the sense of being expressible in terms of relatively Hilbert-Schmidt operators, or equivalently being relatively orthogonal to all relatively weakly mixing functions) is essentially the same concept (after applying the relative spectral theorem) as being approximable by finite rank modules over the base. This goes back (in the ergodic theory setting) to at least the original paper of Furstenberg, who called functions in the latter modules generalised eigenfunctions; see for instance Lemma 7.2 and Theorem 7.4 of Furstenberg’s 1977 paper; the concept is discussed in more detail in Furstenberg’s book, but I don’t have references to that handy at present. Using the Gowers-Host-Kra seminorms (and their duals) in place of the notion of relative weak mixing (and their duals) gives a slightly different tower of factors than Furstenberg’s factors (which is a tower of maximal compact extensions) but at least on the level of the analysis relating to relative almost periodicity, the structure is basically identical.
23 July, 2015 at 12:41 pm
Balazs Szegedy
Ok, this clarifies a lot. I think you have to agree that these classical things have to be re-proved in the ultraproduct setting since this is a new framework (and you did that here). I just wanted to say that I also did that in my sequence of papers on higher order fourier analysis. I was less familiar with classical ergodic theory so I had less background but regardless of this I developed it since I needed that for Higer order fourier analysis. For example your theorem 5 and proposition 7 appers explicitly in my work. If you are not familiar with it then I think it may be relevant to this post and is worth sharing.
23 July, 2015 at 12:52 pm
Terence Tao
Yes, these sorts of results come up in most work on this area. For instance, Theorem 5 of this post is more or less Lemma 5.11 of my 2004 paper translated from standard analysis into nonstandard analysis (and the analogue of Lemma 4.3 of Host-Kra’s 2005 paper), and Proposition 7 is similarly a translated version of Lemma 9.3 of my 2004 paper (and, as mentioned previously, is the analogue of Lemma 7.2 and Theorem 7.4 in Furstenberg’s 1977 paper).
25 July, 2015 at 3:16 am
Balazs Szegedy
Hi Terry,
1.) Thank you for bringing up this concrete question about my nilspace paper with Camarena. The answer is quite short:
It is proved in the paper (see Theorem 2 in section 3.5) that measurable morphisms between nilspaces are continuous. Since translations are automorphisms of nilspaces it follows that measurable translations are continuous.
Such conversations can help in removing opinions that our paper with Camarena “had to be repaired” or contains fundamental flaws.
2.) You are right that many earlier finite statements are basically equivalent with statements proved in the non-standard setting later, but then one might ask “what is the advantage of doing the proofs in the non-standard setting?”.
In my opinion the answer to this question is not just getting rid of epsilon management, but also identifying precise structures in an idealistic infinite setting that appear only in an approximative way in the finite setting. The advantage of this is that it is much easier to work with precise structures than with approximative structures.
I only wanted to say that the program started in my 2009 HOF paper was to identify the approximative structures related to Gowers norms as precise (sometimes algebraic) structures on the appropriate ultraproduct space.
This of course, does not decrease the value and originality of you post. I also have to admit that I was not familiar with your 2004 paper. I will of course cite it in my non-standard papers to explain more the connection between my infinite notions (such as Fourier sigma algebras) and the finite language.
Best,
Balazs
25 July, 2015 at 9:16 pm
Terence Tao
Balazs, in your proof of Theorem 2 on page 39 can you expand on why “The compact nilspace structure on guarantees that
guarantees that  depends continuously on the system
depends continuously on the system  “? It is clear that this is true in a pointwise sense (in that for any
“? It is clear that this is true in a pointwise sense (in that for any  and
and  , that
, that 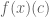 depends continuously on the
depends continuously on the  ); however, the continuity required here is not pointwise but rather in the rather complicated topology of
); however, the continuity required here is not pointwise but rather in the rather complicated topology of  , and to verify continuity in this setting appears to require an additional argument, given that nonlinear continuous functions are usually discontinuous in weak topologies. A model question appears to be to establish that if
, and to verify continuity in this setting appears to require an additional argument, given that nonlinear continuous functions are usually discontinuous in weak topologies. A model question appears to be to establish that if  is a CSM on a factor map
is a CSM on a factor map 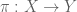 and
and  is a compact abelian group, then the group law on
is a compact abelian group, then the group law on  is continuous. Given your analogy between the topology on
is continuous. Given your analogy between the topology on  and the strong L^1 topology, this is plausible, but of course an analogy is not sufficient by itself to constitute a rigorous proof.
and the strong L^1 topology, this is plausible, but of course an analogy is not sufficient by itself to constitute a rigorous proof.
(Roughly speaking, it seems one needs a relative version of the observation that weak convergence in L^2 plus convergence of norm implies strong convergence in L^2, which you mentioned on page 32 to justify your analogy between the topology and the strong L^1 topology. If one only has the weak convergence that one starts with in the definition of the
topology and the strong L^1 topology. If one only has the weak convergence that one starts with in the definition of the  topology, then it is not obvious that even such a “manifestly continuous” operation as squaring
topology, then it is not obvious that even such a “manifestly continuous” operation as squaring  is actually continuous even when the domain and range of
is actually continuous even when the domain and range of  are compact; note for instance on
are compact; note for instance on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) that the functions
that the functions  converge weakly to 0, but
converge weakly to 0, but  does not converge weakly to 0.)
does not converge weakly to 0.)
26 July, 2015 at 6:16 am
Balazs Szegedy
Hi Terry,
If I understand your question well, the answer relies on a fact about the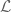 construction. This is that if you have a continuous function of the form
construction. This is that if you have a continuous function of the form  then the function
then the function  defined by composition with
defined by composition with  is continuous. This follows directly from the definition. (Take the basis of continuous functions defining the topology on
is continuous. This follows directly from the definition. (Take the basis of continuous functions defining the topology on 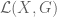 and compose them with
and compose them with 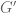 . These compositions are by definition continuous on
. These compositions are by definition continuous on  .)
.)
To spell out why this is enough for the proof I break it down into 4 parts (It seems that your problem was in part 3):
1.) The functions are continuous if
are continuous if 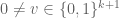 . Based on your question I think that you accepted this part.
. Based on your question I think that you accepted this part.
2.) Let be the function with the property that for every
be the function with the property that for every  we have that
we have that  is the function on
is the function on  whose coordinate functions are
whose coordinate functions are  .
.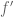 is continuous.
is continuous.
It is clear from the previous statement that
3.) Let denote the set of corners of
denote the set of corners of  dimensional cubes in
dimensional cubes in  . For every
. For every  the function
the function  on
on  takes its values in the closed set
takes its values in the closed set  . Now for every
. Now for every  we compose
we compose  pointwise (!) with the continuous function
pointwise (!) with the continuous function 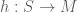 that gives the unique completion of a corner. This way we get the function
that gives the unique completion of a corner. This way we get the function  that appears in the proof and has the property that
that appears in the proof and has the property that 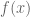 is the constant
is the constant  function on
function on 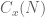 .
.
4.) By the observation I started with we have that these constant functions depend continuously on meaning that the constants also depend continuously.
meaning that the constants also depend continuously.
26 July, 2015 at 6:42 am
Terence Tao
Actually, in your breakdown, the problem is with Step 2. The continuity of the individual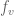 does not “clearly” imply the continuity of
does not “clearly” imply the continuity of 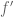 because it is not “clear” that the topology on
because it is not “clear” that the topology on 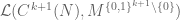 is the product of the topologies on the individual
is the product of the topologies on the individual  . (There are test functions on
. (There are test functions on  that are not linear combinations of functions of a single component
that are not linear combinations of functions of a single component  , but instead depend jointly on all components in a “high-rank” fashion that cannot be easily resolved into one-component functions without taking tensor products, which is an operation which is not obviously continuous with regards to this topology.)
, but instead depend jointly on all components in a “high-rank” fashion that cannot be easily resolved into one-component functions without taking tensor products, which is an operation which is not obviously continuous with regards to this topology.)
To repeat my previous remark, to resolve this issue it appears that one needs a relative version of the classical fact that if a sequence is weakly convergent in L^2 and its norms converge to the norm of the limit, then it is strongly convergent in L^2. But in your setting the measures are varying, and the simple expedient in the classical setting of subtracting a function from its limit is not easily available here.
26 July, 2015 at 1:51 pm
Balazs Szegedy
Hi Terry, I think the following calculation resolves this issue:
Proposition Let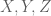 be compact spaces. Let
be compact spaces. Let  be a CSM. Assume that
be a CSM. Assume that 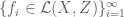 converges to
converges to  and
and  converges to
converges to  such that
such that 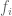 and
and 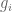 are defined on
are defined on  and
and 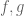 are defined on
are defined on  . Then functions
. Then functions  converge to
converge to  .
.
Proof: We have to show that holds for any pair of continuous functions
holds for any pair of continuous functions  and
and  .
.
First we prove it in the special case when for some continuous functions
for some continuous functions  and
and 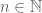 .
.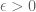 we can construct a
we can construct a 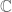 -valued continuous function
-valued continuous function  on
on  with
with  and such that the restriction
and such that the restriction 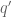 of
of  to
to  has the property that
has the property that  .
.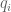 denote the restriction of
denote the restriction of  to
to  . We have by the convergence of
. We have by the convergence of  that
that  converges to
converges to 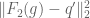 .
.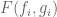 as
as 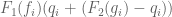 we have that
we have that  and
and  where if
where if  is big enough the
is big enough the  norm each
norm each  and
and  is at most
is at most  . We have by convergence of
. We have by convergence of  that
that
For any fixed
Let
Now writing
It follows from the previous estimates that
By converging to with
with  we obtain the statement.
we obtain the statement.
Using Stone-Weierstrass we can approximate every two variable continuous function on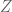 by a linear combination of functions of the form
by a linear combination of functions of the form  . This completes the proof.
. This completes the proof.
27 July, 2015 at 7:44 am
Terence Tao
Balazs, thanks for this argument. It seems that this, together with the expanded argument provided previously for the proof of Theorem 2, as well as suitable clarification of the proof of Lemma 3.23 (in particular explaining why the translation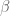 is first Borel measurable, and then continuous) does indeed finally repair the issue I raised with you in my Nov 8 2010 email. (Incidentally, there is a further confusing typo in the proof of Lemma 3.23: it appears that you reference Lemma 2.1 when you should instead be referencing the rather different Proposition 2.1. This issue may also occur elsewhere in the paper, it is worth checking.)
is first Borel measurable, and then continuous) does indeed finally repair the issue I raised with you in my Nov 8 2010 email. (Incidentally, there is a further confusing typo in the proof of Lemma 3.23: it appears that you reference Lemma 2.1 when you should instead be referencing the rather different Proposition 2.1. This issue may also occur elsewhere in the paper, it is worth checking.)
I have some other questions about your 2010 paper with Camarena, relating more to the relationship between your paper and various concepts and results introduced in previous literature, including the 2005 paper [HK2005] of Host and Kra (reference [10] in your paper), the 2006 paper [HK2006] of Host and Kra (reference [11] in your paper), and a 2009 paper [HKM2009] of Host, Kra, and Maass (which you might not be aware of, as it is not referenced in your paper; see also the precursor [HM2006] to [HKM2009]).
27 July, 2015 at 11:14 am
Terence Tao
p.s. there may also be a link between the rigidity result in your Theorem 2 (that measurable morphisms are continuous) and the property testing literature, for instance this 2004 paper of Alon, Kaufman, Krivelevich, Litsyn, and Ron, in which they show that the property of being a polynomial of given degree over is locally testable with one-sided error (the linear case being a famous paper of Blum, Luby, and Rubinfeld). In particular, the arguments in Section 4 of that paper remind me of the combinatorial manipulations on the three-cube in your paper, and the key property of a polynomial used is that its value at one corner of a parallelepiped is determined by its value at all other corners. (The technical details are of course a little different, for instance the alternating signs in the sums are not explicit in the AKKLR paper because they work in characteristic two. Still there seems to be some connection; it may be for instance that taking an ultraproduct of a sequence of instances of functions that locally test to be polynomial in the AKKLR sense leads to a measurable morphism to which your Theorem 2 may be applied. This would be in analogy with how property testing for graph properties interacts well with graph limits, as noted for instance in Lovasz’s book.) This is of course also closely related to the topic of the inverse conjecture for Gowers norms over finite fields.
is locally testable with one-sided error (the linear case being a famous paper of Blum, Luby, and Rubinfeld). In particular, the arguments in Section 4 of that paper remind me of the combinatorial manipulations on the three-cube in your paper, and the key property of a polynomial used is that its value at one corner of a parallelepiped is determined by its value at all other corners. (The technical details are of course a little different, for instance the alternating signs in the sums are not explicit in the AKKLR paper because they work in characteristic two. Still there seems to be some connection; it may be for instance that taking an ultraproduct of a sequence of instances of functions that locally test to be polynomial in the AKKLR sense leads to a measurable morphism to which your Theorem 2 may be applied. This would be in analogy with how property testing for graph properties interacts well with graph limits, as noted for instance in Lovasz’s book.) This is of course also closely related to the topic of the inverse conjecture for Gowers norms over finite fields.
26 July, 2015 at 5:03 am
Ben Green
Balazs, I think this conversation highlights the frustration felt by those of us who spent time trying to read your papers. The argument is incomplete from the standpoint of a human reader of the papers, by which I mean that there is too much to be filled in between the lines. At least, I found this to be the case. That’s not to suggest that it’s not a subset of a complete argument, quite possibly an everywhere dense one. Indeed the results (some known by other means) as well as the methods are quite natural.
The problem is compounded by the fact that the notation and the number of definitions and names make the paper extremely heavy reading, and by the fact that from 2009-2012 there were a large number of rather different new versions of the work posted on the arxiv. It looks as if things have stabilised with the 2012 version, which addresses the second issue. As regards the first, I think the community would universally appreciate a greatly expanded version of the complete argument, quite possibly illustrated in the 2-step case throughout. As I understand it, that case contains essentially all of the ideas whilst being much lighter on general notation.
Best wishes, Ben
27 July, 2015 at 8:18 am
Balazs Szegedy
Hi Ben,
Thank you for your comment.
First, the part that I mostly agree with. I take your phrase “everywhere dense argument” as a positive critique. I think what you mean is that the results are correctly broken down into lemmas, but the expositions of the proofs of the individual lemmas are of varying quality. I was definitely more busy (and interested) in breaking through the fundamental difficulties and finding the right inherent language than perfecting the exposition. I am taking responsibility for that.
A particular weakness in the exposition of the nilspace paper is that it builds on the subject of “continuous systems of measures” CSM’s. Quite surprisingly, this fundamental subject was not developed enough for our purposes. So with Omar we had to do a lot of ground work in it. Terry’s question was also basically about the behavior of CSM’s. I think that the best idea is to publish a separate paper that cleans up the CSM subject and thus making the paper more understandable by freeing it from this burden. We actually plan to write such a paper with Pablo Candela.
As of the history of my papers on the ArXiv I partially disagree with you. When I wrote my first paper in 2009 I observed that many non standard arguments that we developed for hypergraphs with Elek in 2007 can be also applied for the Gowers norms and I wanted to explore how far one can go with these ideas. So I wrote a sequence of 3 papers, mainly built on my paper with Elek and of course on the fundamental work of Host and Kra. Only at the end of the third paper it became clear to me that this leads to a theory of additive structures in compact abelian groups. My main goal was not to prove the inverse theorem. I look at it as a byproduct of a more general clean structure theory of characteristic factors on ultraproduct groups. I think that already my work in 2010 clearly demonstrates that I had all the fundamental ideas for such a structure theory. It was not a 2 page sketch, the math is there. You are right that it stabilized in a new version in 2012 when I changed some arguments to new ones that I felt more aesthetic.
I will try my best to come up with a version that is more pleasant to read and I am glad to take any advise from you give on how to do it.
Best,
Balazs
27 July, 2015 at 8:58 am
Ben Green
Balazs – yes, the expositions are of varying quality. I look forward to a fully fleshed out version of the arguments in due course. Best, Ben.
30 July, 2015 at 3:08 pm
A Phrase Is Born
Ben, that phrase “everywhere dense subset of a complete argument” is a gem that deserves wider circulation. Did you invent it?
27 July, 2015 at 4:07 am
Victor
@Balazs
I am not familiar with this area but I was curious. Since it’s much easier to work with precise structures in the infinite setting, are there any new results in the finite setting that one can obtain using these precise structures that were not known before using the approximate structures?
27 July, 2015 at 5:13 am
Balazs Szegedy
Hi Victor there is a standard machinery including furstenberg’s correspondence principle and the transference principle for ultraproducts that allows you to translate back anything that you do in the idealistic infinite universe to the finite setting. This is the way for example how Furstenberg proved Szemeredi’s theorem (which can be regarded as a finite statement) using infinite arguments. There are many finite statements that have much easier proofs in the infinite setting and of corse statements that had their first proofs in the infinite setting.
27 July, 2015 at 8:23 am
Victor
@all
Again, to satisfy my curiosity I would like to see mentioned a couple of examples of statements that had their first proofs in the infinite setting.
29 July, 2015 at 5:15 am
Anonymous
Density Hales-Jewett is a not-completely-bad example.
29 July, 2015 at 11:30 am
Victor
That’s a good example, thanks! I don’t understand why people took my question so negatively…
28 July, 2015 at 12:56 am
Balazs Szegedy
It is very much true that my whole work (in every aspect) can be regarded as a continuation of the work of Host and Kra starting with my 2009 paper which is built almost exclusively on the famous Annals paper of them on characteristic factors and my paper with Elek. I regard the nilspace paper as just a continuation of the Host-Kra paper on parallelepiped structures and we say it very clearly in the abstract but you are right that we should do a better job with citations throughout the paper. In a new version I will fix this. The main difficulty that we treat with Camarena is the topologization of the language of Host and Kra. The real novelty in the paper is in the methods that we developed for this topologization. (In my application in Higher order Fourier analysis I needed a topological version.)
Personally I am a big fan of the work of Host and Kra as they had the right vision from very early on and I am glad that I could contribute to it.
30 July, 2015 at 11:33 am
Yonatan
Dear Terry,
I would like to make some brief comments regarding the questions you posed above:
Q2 One possible explanation for the “striking parallels between the ergodic theory context and the compact nilspace context” is contained in some recent unpublished work of mine building heavily on the work of Host-Kra and Camarena-Szegedy . Essentially, one can show directly — i.e., without using the structure theory of [HK2005] — that the Host-Kra characteristic factors have (compact) topological (dynamical) models which carry compatible (with the dynamics) compact nilspace structure. This allows the structure theorem of [HK2005] to be *deduced* from a dynamical variant of the Camarena-Szegedy structure theorem for nilspaces due to Freddie Manners, Péter Varjú and myself.
Q3 Let be an arbitrary topological group and let
be an arbitrary topological group and let  be a topological dynamical system. Define a “dynamical” cubespace by (
be a topological dynamical system. Define a “dynamical” cubespace by ( )
)
![C_{G}^{n}(X)=\overline{\{HK^{n}(G)(x,x,\ldots,x)|\,x\in X\}}\subset X^{[n]}](https://s0.wp.com/latex.php?latex=C_%7BG%7D%5E%7Bn%7D%28X%29%3D%5Coverline%7B%5C%7BHK%5E%7Bn%7D%28G%29%28x%2Cx%2C%5Cldots%2Cx%29%7C%5C%2Cx%5Cin+X%5C%7D%7D%5Csubset+X%5E%7B%5Bn%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) (
( is the Host-Kra cubegroup). For
is the Host-Kra cubegroup). For  abelian this is
abelian this is  . Following Camarena-Szegedy define the relation
. Following Camarena-Szegedy define the relation  if
if 
If is abelian and
is abelian and  is minimal then it follows from the works of Host-Kra-Maass and Shao-Ye that
is minimal then it follows from the works of Host-Kra-Maass and Shao-Ye that  is an equivalence relation.
is an equivalence relation. is arbitrary and
is arbitrary and  is minimal distal then
is minimal distal then 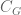 is a prenilspace (cubespace with
is a prenilspace (cubespace with  -completion for all
-completion for all  ) and therefore
) and therefore  is an equivalence relation.
is an equivalence relation.
By a result of Freddie Manners, Péter Varjú and myself If
Using the dynamical variant of the Camarena-Szegedy structure theorem alluded to above one can conclude that in all of these cases is the maximal pronilfactor of (H,X) of degree k (for
is the maximal pronilfactor of (H,X) of degree k (for  it was already known from Host-Kra-Maass).
it was already known from Host-Kra-Maass).
Eli Glasner and myself constructed a minimal example (a proximal extension of a rotation) for which
minimal example (a proximal extension of a rotation) for which 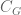 is not a prenilspace.
is not a prenilspace.
Best wishes,
Yonatan
6 September, 2017 at 6:28 am
espressonator
I wish I could work with you, Professor Tao, on some nonstandard mathematics aimed at solving some (hard) open problems. You see things so quickly, it’s nice to read your blog posts and watch your youtube presentations.