One of the key difficulties in performing analysis in infinite-dimensional function spaces, as opposed to finite-dimensional vector spaces, is that the Bolzano-Weierstrass theorem no longer holds: a bounded sequence in an infinite-dimensional function space need not have any convergent subsequences (when viewed using the strong topology). To put it another way, the closed unit ball in an infinite-dimensional function space usually fails to be (sequentially) compact.
As compactness is such a useful property to have in analysis, various tools have been developed over the years to try to salvage some sort of substitute for the compactness property in infinite-dimensional spaces. One of these tools is concentration compactness, which was discussed previously on this blog. This can be viewed as a compromise between weak compactness (which is true in very general circumstances, but is often too weak for applications) and strong compactness (which would be very useful in applications, but is usually false), in which one obtains convergence in an intermediate sense that involves a group of symmetries acting on the function space in question.
Concentration compactness is usually stated and proved in the language of standard analysis: epsilons and deltas, limits and supremas, and so forth. In this post, I wanted to note that one could also state and prove the basic foundations of concentration compactness in the framework of nonstandard analysis, in which one now deals with infinitesimals and ultralimits instead of epsilons and ordinary limits. This is a fairly mild change of viewpoint, but I found it to be informative to view this subject from a slightly different perspective. The nonstandard proofs require a fair amount of general machinery to set up, but conversely, once all the machinery is up and running, the proofs become slightly shorter, and can exploit tools from (standard) infinitary analysis, such as orthogonal projections in Hilbert spaces, or the continuous-pure point decomposition of measures. Because of the substantial amount of setup required, nonstandard proofs tend to have significantly more net complexity than their standard counterparts when it comes to basic results (such as those presented in this post), but the gap between the two narrows when the results become more difficult, and for particularly intricate and deep results it can happen that nonstandard proofs end up being simpler overall than their standard analogues, particularly if the nonstandard proof is able to tap the power of some existing mature body of infinitary mathematics (e.g. ergodic theory, measure theory, Hilbert space theory, or topological group theory) which is difficult to directly access in the standard formulation of the argument.
— 1. Weak sequential compactness in a Hilbert space —
Before turning to concentration compactness, we will warm up with the simpler situation of weak sequential compactness in a Hilbert space. For sake of notation we shall only consider complex Hilbert spaces, although all the discussion here works equally well for real Hilbert spaces.
Recall that a bounded sequence of vectors in a Hilbert space
is said to converge weakly to a limit
if one has
for all
. We have the following basic theorem:
Theorem 1 (Sequential Banach-Alaoglu theorem) Every bounded sequence
of vectors in a Hilbert space
has a weakly convergent subsequence.
The usual (standard analysis) proof of this theorem runs as follows:
Proof: (Sketch) By restricting to the closed span of the , we may assume without loss of generality that
is separable. Letting
be a dense subet of
, we may apply the Bolzano-Weierstrass theorem iteratively, followed by the Arzelá-Ascoli diagonalisation argument, to find a subsequence
for which
converges to a limit for each
. Using the boundedness of the
and a density argument, we conclude that
converges to a limit for each
; applying the Riesz representation theorem for Hilbert spaces, the limit takes the form
for some
, and the claim follows.
However, this proof does not extend easily to the concentration compactness setting, when there is also a group action. For this, we need a more “algorithmic” proof based on the “energy increment method”. We give one such (standard analysis) proof as follows:
Proof: As is bounded, we have some bound of the form
for some finite . Of course, this bound would persist if we passed from
to a subsequence.
Suppose for contradiction that no subsequence of was weakly convergent. In particular,
itself was not weakly convergent, which means that there exists
for which
did not converge. We can take
to be a unit vector. Applying the Bolzano-Weierstrass theorem, we can pass to a subsequence (which, by abuse of notation, we continue to call
) in which
converged to some non-zero limit
. We can choose
to be nearly maximal in magnitude among all possible choices of subsequence and of
; in particular, we have
(say) for all other choices of unit vector .
We may now decompose
where is orthogonal to
and
converges strongly to zero. From Pythagoras theorem we see that
asymptotically has strictly less energy than
:
If was weakly convergent, then
would be too, so we may assume that it is not weakly convergent. Arguing as before, we may find a unit vector
(which we can take to be orthogonal to
) and a constant
such that (after passing to a subsequence, and abusing notation once more) one had a decomposition
in which is orthogonal to both
and
converges strongly to zero, and such that
for all unit vectors . From Pythagoras, we have
We iterate this process to obtain an orthonormal sequence and constants
obeying the Bessel inequality
(which, in particular, implies that the go to zero as
) such that, for each
, one has a subsequence of the
for which one has a decomposition of the form
where converges strongly to zero, and for which
for all unit vectors . The series
then converges (conditionally in the strong topology) to a limit
, and by diagonalising all the subsequences we obtain a final subsequence
which converges weakly to
.
Now we give a third proof, which is a nonstandard analysis proof that is analogous to the second standard analysis proof given above.
The basics of nonstandard analysis are reviewed in this previous blog post (and see also this later post on ultralimit analysis, as well as the most recent post on this topic). Very briefly, we will need to fix a non-principal ultrafilter on the natural numbers. Once one fixes this ultrafilter, one can define the ultralimit
of any sequence of standard objects
, defined as the equivalence class of all sequences
such that
. We then define the ultrapower
of a standard set
to be the collection of all ultralimits
of sequences
in
. We can interpret
as the space of all nonstandard elements of
, with the standard space
being embedded in the nonstandard one
by identifying
with its nonstandard counterpart
. One can extend all (first-order) structures on
to
in the obvious manner, and a famous theorem of Los asserts that all first-order sentences that are true about a standard space
, will also be true about the nonstandard space
. Thus, for instance, the ultrapower
of a standard Hilbert space
over the standard complex numbers
will be a nonstandard Hilbert space
over the nonstandard reals
or the nonstandard complex numbers
. It has a nonstandard inner product
instead of a standard one, which obeys the nonstandard analogue of the Hilbert space axioms. In particular, it is complete in the nonstandard sense: any nonstandard Cauchy sequence
of nonstandard vectors
indexed by the nonstandard natural numbers
will converge (again, in the nonstandard sense) to a limit
.
The ultrapower – the space of ultralimits
of arbitrary sequences
in
– turns out to be too large and unwieldy to be helpful for us. We will work instead with a more tractable subquotient, defined as follows. Let
be the space of ultralimits
of bounded sequences
, and let
be the space of ultralimits
of sequences
that converge to zero. It is clear that
,
are vector spaces over the standard complex numbers
, with
being a subspace of
. (The space
is also known as the monad of the origin of
.) We define the quotient space
, which is then also a vector space over
. One easily verifies that
is a subspace of
that is disjoint from
, so we can embed
as a subspace of
.
Remark 2 When
is finite dimensional, the Bolzano-Weierstrass theorem (or more precisely, the proof of this theorem) shows that
. For infinite-dimensional spaces, though,
is larger than
, basically because there exist bounded sequences in
with no convergent subsequences. Thus we can view the quotient
as measuring the failure of the Bolzano-Weierstrass theorem (a sort of “Bolzano-Weierstrass cohomology”, if you will).
Now we place a Hilbert space structure on . Observe that if
and
are elements of
(so that
are bounded), then the nonstandard inner product
is a nonstandard complex number which is bounded (i.e. it it lies in
). Since
, we can thus extract a standard part
, defined as the unique standard complex number such that
where denotes an infinitesimal, i.e. a non-standard quantity whose magnitude is less than any standard positive real
. From the Cauchy-Schwarz inequality we see that if we modify either
or
by an element of
, then the standard part
does not change. Thus, we see that the map
on
descends to a map
on
. One easily checks that this map is a standard Hermitian inner product on
that extends the one on the subspace
. (If one prefers to think in terms of commutative diagrams, one can think of the inner product as a bilinear map from the short exact sequence
to the short exact sequence
.) Furthermore, by using the countable saturation (or Bolzano-Weierstrass) property of nonstandard analysis (see previous post), we can also show that
is complete with respect to this inner product; thus
is a standard Hilbert space that contains
as a subspace. (One can view
as a sort of nonstandard completion of
, in a manner somewhat analogous to how the Stone-Cech compactification
of a space can be viewed as a topological completion of
. This is of course consistent with the philosophy of the previous post.)
After all this setup, we can now give the third proof of Theorem 1:
Proof: Let be the ultralimit of the
, then
is an element of
. Let
be the image of
in
, and let
be the orthogonal projection of
to
. We claim that a subsequence of
converges weakly to
.
For any ,
is orthogonal to
, and thus
. In other words,
for all . This is already the nonstandard analogue of weak convergence along a subsequence, but we can get to weak convergence itself with only a little more argument. Indeed, from (1) we can easily construct a subsequence
such that
and
for all , which implies that
whenever is a finite linear combination of the
and
. Applying a density argument using the boundedness of the
, this is then true for all
in the closed span of the
and
; it is also clearly true for
in the orthogonal complement, and the claim follows.
Observe that in contrast with the first two proofs, the third proof gave a “canonical” choice for the subsequence limit . This is ultimately because the ultrafilter
already “made all the choices beforehand”, in some sense.
Observe also that we used the existence of orthogonal projections in Hilbert spaces in the above proof. If one unpacks the usual proof that these projections exist, one will find an energy increment argument that is not dissimilar to that used in the second proof of Theorem 1. Thus we see that the somewhat intricate energy increment argument from that second proof has in some sense been encapsulated into a general-purpose package in the nonstandard setting, namely the existence of orthogonal projections.
— 2. Concentration compactness for unitary group actions —
Now we generalise the sequential Banach-Alaoglu theorem to allow for a group of symmetries. The setup is now that of a (standard) complex vector space , together with a locally compact group
acting unitarily on
in a jointly continuous manner, thus the map
is jointly continuous from
to
(or equivalently, the representation map from
to
is continuous if we give
the strong operator topology). We also assume that
is a group of dislocations, which means that
converges weakly to zero in
whenever
and
goes to infinity in
(which means that
eventually escapes any given compact subset of
). A typical example of such a group is the translation action
of
on
, another example is the scaling action
of
on
. (One can also combine these two actions to give an action of the semidirect product
on
.)
The basic theorem here is
Theorem 3 (Profile decomposition) Let
be as above. Let
be a bounded sequence in
obeying the energy bound
Then, after passing to a subsequence, one can find a sequence
with the Bessel inequality
and group elements
for
such that
whenever
and
are non-zero, such that for each
one has the decomposition
such that
and
for all unit vectors
, and such that
converges weakly to zero for every
.
Note that Theorem 1 is the case when is trivial.
There is a version of the conclusion available in which can be taken to be infinite, and also one can generalise
to be a more general object than a group by modifying the hypotheses somewhat; see this paper of Schindler and Tintarev. The version with finite
is slightly more convenient though for applications to nonlinear dispersive and wave equations; see these lecture notes of Killip and Visan for some applications of this type of decomposition. In order for this theorem to be useful for applications, one needs to exploit some sort of inverse theorem that controls other norms of a vector
in terms of expressions such as
; these theorems tend to require “hard” harmonic analysis and cannot be established purely by such “soft” analysis tools as nonstandard analysis.
One can adapt the second proof of Theorem 1 to give a standard analysis proof of Theorem 3:
Proof: (Sketch) Applying Theorem 1 we can (after passing to a subsequence) find group elements such that
converges weakly to a limit
, which we can choose to be nearly maximal in the sense that
(say) whenever is the weak limit of
for some subsequence
and some collection of group elements
. In particular, this implies (from further application of Theorem 1, and an argument by contradiction) that
for any unit vector .
We may now decompose
where converges weakly to zero. From Pythagoras theorem we see that
asymptotically has strictly less energy than
:
We then repeat the argument, passing to a further subsequence and finding group elements such that
converges weakly to
, with
for any unit vector .
Note that converges weakly to zero, while
converges weakly to
. If
is non-zero, this implies that
must go to infinity (otherwise it has a convergent subsequence, and this soon leads to a contradiction).
If one iterates the above construction and passes to a diagonal subsequence one obtains the claim.
Now we give the nonstandard analysis proof. As before, we introduce the short exact sequence of Hilbert spaces:
We will also need an analogous short exact sequence of groups
where is the space of ultralimits
of sequences
in
that lie in a compact subset of
, and
is the space of ultralimits of
of sequences
that converge to the identity element (i.e.
is the monad of the group identity). One easily verifies that
is a normal subgroup of
, and that the quotient is isomorphic to
. (Indeed,
can be expressed as a semi-direct product
, though we will not need this fact here.)
The group acts unitarily on
, and so preserves both
and
. As such, it also acts unitarily on
. The induced action of the subgroup
is trivial; and the induced action of the subgroup
preserves
.
Let be the closed span of the set
in
; this is a Hilbert space. Inside this space we have the subspaces
for
. As
preserves
, we see that
whenever
lie in the same coset of
, so we can define
for any
in a well-defined manner. On the other hand, if
do not lie in the same coset of
, then we have
for some sequence
in
that goes to infinity. As
is a group of dislocations, we conclude that
and
are now orthogonal. In other words,
and
are orthogonal whenever
are distinct. We conclude that we have the decomposition
where is the Hilbert space direct sum.
Now we can prove Theorem 3. As in the previous section, starting with a bounded sequence in
, we form the ultralimit
and the image
. We let
be the orthogonal projection of
to
. By (2), we can write
for some at most countable sequence of vectors and
, with the
lying in distinct cosets of
. In particular, for any
,
is the ultralimit of a sequence of vectors going to infinity. By adding dummy values of
if necessary we may assume that
ranges from
to infinity. Also, one has the Bessel inequality
and from Cauchy-Schwarz and Bessel one has
for any unit vector and
. From this we can obtain the required conclusions by arguing as in the previous section.
— 3. Concentration compactness for measures —
We now give a variant of the profile decomposition, for Borel probability measures on
. Recall that such a sequence is said to be tight if, for every
, there is a ball
such that
. Given any Borel probability measure
on
and any
, define the translate
to be the Borel probability measure given by the formula
.
Theorem 4 (Profile decomposition for probability measures on
) Let
be a sequence of Borel probability measures on
. Then, after passing to a subsequence, one can find a sequence
of non-negative real numbers with
, a tight sequence
of positive measures whose mass converges to
as
for fixed
, and shifts
such that
for all
, and such that for each
, one has the decomposition
where the error
obeys the bounds
and
for all radii
and
.
Furthermore, one can ensure that for each,
converges in the vague topology to a probability measure
.
We first give the standard proof of this theorem:
Proof: (Sketch) Suppose first that
for all . Then we are done by setting all the
equal to zero, and
. So we may assume that we can find
such that
for some ; we may also assume that
is approximately maximal in the sense that
(say) for all other radii . By passing to a subsequence, we may thus find
such that
By passing to a further subsequence using the Helly selection principle (or the sequential Banach-Alaoglu theorem), we may assume that the translates converge in the vague topology to a limit of total mass at most
and at least
, and which can be expressed as
for some
and a probability measure
.
As converges vaguely to
, we have
for any . By making
grow sufficiently slowly to infinity with respect to
, we may thus ensure that
for all integers . If we then set
to be the restriction of
to
, we see that
is tight, converges vaguely to
, and has total mass converging to
. We can thus split
for some residual positive measure of total mass converging to
, and such that
as
for any fixed
. We can then iterate this procedure to obtain the claims of the theorem (after one last diagonalisation to combine together all the subsequences).
Now we give the nonstandard proof. We take the ultralimit of the standard Borel probability measures
on
, resulting in a nonstandard Borel probability measure. What, exactly, is a nonstandard Borel probability measure? A standard Borel probability measure, such as
, is a map
from the standard Borel
-algebra
to the unit interval
which is countably additive and maps
to
. Thus, the nonstandard Borel probability measure is a nonstandard map
from the nonstandard Borel
-algebra (the collection of all ultralimits of standard Borel sets) to the nonstandard interval
which is nonstandardly countably additive and maps
to
. In particular, it is finitely additive.
There is an important subtlety here. The nonstandard Borel -algebra is closed under nonstandard countable unions: if
is a nonstandard countable sequence of nonstandard Borel sets (i.e. an ultralimit of standard countable sequences
of standard Borel sets), then
is also nonstandard Borel, but this is not necessarily the case for external countable unions, thus if
is an external countable sequence of nonstandard Borel sets, then
need not be nonstandard Borel. On the other hand,
is certainly still closed under finite unions and other finite Boolean operations, so it can be viewed (externally) as a Boolean algebra, at least.
Now we perform the Loeb measure construction (which was also introduced in the previous post). Consider the standard part of
; this is a finitely additive map from
to
. From the countable saturation property, one can verify that this map is a premeasure, and so (by the Hahn-Kolmogorov theorem) extends to a countably additive probability measure
on the measure-theoretic completion
of
.
The measure is a measure on
. We push it forward to the quotient space
by the obvious quotient map
to obtain a pushforward measure
on the pushforward
-algebra
, which consists of all (external) subsets
of
whose preimage
is measurable in
.
We claim that every point in is measurable in
, or equivalently that every coset
in
is measurable in
. Indeed, this coset is the union of the countable family of (nonstandard) balls
for
, each one of which is a nonstandard Borel set and thus measurable in
.
Because of this, we can decompose the measure into pure point and singular components, thus
where are standard non-positive reals,
ranges over an at most countable set,
are disjoint cosets in
, and
is a finite measure on
such that
and
for every coset .
Now we analyse the restriction of to a single coset
, which has total mass
. For any standard continuous, compactly supported function
, one can form the integral
This is a non-negative continuous linear functional, so by the Riesz representation theorem there exists a non-negative Radon measure on
such that
for all such . As
has total mass
,
is a probability measure. From definition of
, we thus have
for all .
We have
for every standard , and thus by the overspill principle there exists an unbounded
for which
since , we thus have
If we set to be the restriction of
to
, we thus see that
for all test functions . Writing
as the ultralimit of probability measures
, we thus see (upon passing to a subsequence) that
converges vaguely to the probability measure
, and is in particular tight.
For any standard , we can write
where is a finite measure. Letting
be the Loeb extension of the standard part of
, we see that
assigns zero mass to
for
and assigns a mass of at most
to any other coset of
. This implies that
for any standard . Expressing
as an ultralimit of
, we then obtain the claim.

21 comments
Comments feed for this article
29 November, 2010 at 1:43 pm
Anonymous
Prof. Tao, do you intend to teach a course in nonstandard analysis?
29 November, 2010 at 4:24 pm
Terence Tao
The short answer is no (any more than I would teach a course on, say, the construction of number systems; it is too foundational a subject for the type of course topics I have in mind). But there may be occasion to develop some nonstandard arguments within a broader course topic. For instance, in my 254B course on higher order Fourier analysis last year, I mentioned the nonstandard approach to equidistribution, for instance in Notes 1 of that course. Somewhat relatedly, I also mentioned the ultrafilter approach to Ramsey theory in my 254A course on ergodic theory from the previous year (see e.g. Notes 3 from that course).
29 November, 2010 at 6:10 pm
Anonymous
The course on ergodic theory should be “254A” :) [Corrected, thanks – T.]
30 November, 2010 at 4:48 am
Anonymous
Prof. Tao,
Which courses are you planning to teach in near future? I hope you teach a grad level complex analysis and probability theory…
Thanks
29 November, 2010 at 5:12 pm
notedscholar
I wonder if you have read my work on Infinity? I do not want to link which would be inappropriate, but just asking.
Cheers,
NS
30 November, 2010 at 11:56 am
Ulrich Kohlenbach
Dear Terry,
many thanks for your interesting posting.
In connection with your treatment of the sequential weak compactntess in Hilbert space I like to mention three recent papers of mine:
1) In my paper “Goedel functional interpretation and weak compactness”
(available at http://www.mathematik.tu-darmstadt.de/~kohlenbach/weakcompactness-els.pdf )
I carry out (a variant version) of the Goedel “Dialectica” interpretation of the standard proof for the weak compactness as sketched in your posting. This results in a certain effective functional Omega* that comprises the computational content of that principle in the sense that it is precisely Omega* that is needed to extract bounds from proofs of combinatorial statements that use weak compactness. Omega* is primitive recursive in Spector’s bar recursion of lowest type. This is optimal in the sense that already the usual Bolzano-Weierstrass principle [0,1] requires this. In particular, Omega* locally stays within Goedel’s primitive recursive functionals of finite type. The construction also uses energy increment ideas. It would be interesting to see whether your 2nd proof results in a simpler bound that e.g. may need only one use of bar recursion (corresponding to the use of the Bolzano-Weierstrass principle) whereas I have a 2nd use corresponding to the Riesz representation theorem.
2) In “A uniform quantitative version of sequential weak compactness
and Baillon’s nonlinear ergodic theorem” (also available from the above
site) I use Omega* to extract an explicit uniform bound on a metastable
(in your sense) version of Baillon’s nonlinear ergodic theorem.
3) Interestingly, when weak compactness is used to prove a strong convergence result, the quantitative analysis in the spirit of Goedel’s
interpretation often seems to be able to eliminate weak compactness
altogether: see my recent paper:
“On quantitative versions of theorems due to F.E. Browder and R. Wittmann. Advances in Mathematics 226, pp. 2764-2795 (2011).
With best regards,
Ulrich
30 November, 2010 at 9:18 pm
Bright, YU
Hi, Terry. I wanna ask a question not directly related to this post, but somehow I find it interesting and maybe you have an answer to it.
Suppose u is a harmonic function on the Euclidean Plane, given (x,y),then by Mean Value Property, u(x,y) should equals the mean value of u along a circle with radius r centred at (x,y).
With the mean value theorem for integral, u should attains the value at some point(s), say (m,n) on the circle.
SO, my question is that what is the set of such points if we pick one (m,n) on each circle and let r range from 0 to infinity?
Looking forward to your reply.
Bright, YU
2 December, 2010 at 9:24 am
J.P. McCarthy
Bright,
Your question is a bit on the general side.
For example, for a constant function, the set of points (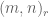 ?) is the entire circle for all
?) is the entire circle for all  .
.
For a linear function, such as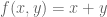 , the set of points
, the set of points  , if we choose for example
, if we choose for example 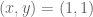 , is going to correspond to half of the circle (a picture will show you which half).
, is going to correspond to half of the circle (a picture will show you which half).
If however you pick the points are always going to be those corresponding to
the points are always going to be those corresponding to 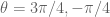 .
.
J.P.
4 December, 2010 at 4:51 pm
iori1986iori
大哥,你好强悍!big brother, u really smart
6 December, 2010 at 10:14 pm
katz
I have a naive question. Is this related to concentration of measure (around a median) a la Paul Levy and vitaly Milman?
7 December, 2010 at 10:44 am
Terence Tao
As far as I know there is no connection. Concentration of measure is ultimately coming from the law of large numbers, whereas the type of concentration on subsequences seen here is coming from things like the Bolzano-Weierstrass theorem. In both cases there is convergence to a limit, but other than that there appears to be no further relationship.
13 December, 2010 at 1:08 am
Igor Carron
Terry,
I have checked with both my blogging software (in my Blog list) and Google reader and it looks like your RSS feed has stopped as of December 6th. The last entry I get has the title: “Strongly dense fre”. I just re-subscribed to your feed and get the same result. If I am the only one to get this then sorry, if not…
Cheers,
Igor.
16 December, 2010 at 12:19 am
Qiaochu Yuan
This happened to me as well. I can’t imagine what would cause this. Perhaps the feed has a maximum size which has been exceeded?
17 December, 2010 at 2:06 am
Igor Carron
It’s fixed now. Thanks.
15 December, 2010 at 6:01 am
Avery Carr
Prof. Tao,
Can Concentration Compactness be applied to the Invariant Subspace Problem for Hilbert Spaces? Thank you.
Avery Carr
9 April, 2011 at 7:04 pm
peter p.
Apparently, P.L. Lions makes the comment in his 1984 paper that “This crucial lemma is proved with the help of the notion of the concentration function of a measure -introduced by P. Levy [14]”. He was referring to the concentration compactness lemma, I think, which occupies a big portion of his paper. Maybe worth a look.
4 August, 2011 at 6:53 pm
Localisation and compactness properties of the Navier-Stokes global regularity problem « What’s new
[…] symmetry that is available for the space . (Concentration compactness is discussed in these previous blog posts.) One then has to deal with sequences of data that are not strongly convergent, but are […]
15 October, 2011 at 10:58 am
254A, Notes 6: Ultraproducts as a bridge between hard analysis and soft analysis « What’s new
[…] two constructions are at least partially interchangeable in this setting. (See also these previous posts for the use of ultralimits as a substitute for topological limits.) In the theory of approximate […]
25 October, 2012 at 10:10 am
Walsh’s ergodic theorem, metastability, and external Cauchy convergence « What’s new
[…] us to reduce the need to invoke the nonstandard measure theory of Loeb, discussed for instance in this blog post); we will use the notion of a (real) commutative probability space , which for us will be a […]
7 December, 2013 at 4:06 pm
Ultraproducts as a Bridge Between Discrete and Continuous Analysis | What's new
[…] analysis can be used as a framework to describe the theory of concentration compactness; see this previous blog post for further discussion. Finally, if one starts with a finitely generated group with a word metric […]
4 January, 2021 at 6:46 am
Go 2 It
Some typos:
in the middle of section 2, “do not lie in the same coset of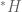 “: should be
“: should be 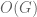
in the nonstandard proof of theorem 3, “nonstandard interval![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002) “: should be
“: should be ![{}^* [0,1]](https://s0.wp.com/latex.php?latex=%7B%7D%5E%2A+%5B0%2C1%5D&bg=ffffff&fg=545454&s=0&c=20201002)
following “obvious quotient map”, missing “ ”
”
[Corrected, thanks – T.]