Ultraproducts as a Bridge Between Discrete and Continuous Analysis

7 December, 2013 in expository, math.CA, math.CO, math.DS, math.LO, talk | Tags: correspondence principle, Loeb measure, nonstandard analysis, regularity lemma, ultrafilters, ultraproducts

(This is an extended blog post version of my talk “Ultraproducts as a Bridge Between Discrete and Continuous Analysis” that I gave at the Simons institute for the theory of computing at the workshop “Neo-Classical methods in discrete analysis“. Some of the material here is drawn from previous blog posts, notably “Ultraproducts as a bridge between hard analysis and soft analysis” and “Ultralimit analysis and quantitative algebraic geometry“‘. The text here has substantially more details than the talk; one may wish to skip all of the proofs given here to obtain a closer approximation to the original talk.)

Discrete analysis, of course, is primarily interested in the study of discrete (or “finitary”) mathematical objects: integers, rational numbers (which can be viewed as ratios of integers), finite sets, finite graphs, finite or discrete metric spaces, and so forth. However, many powerful tools in mathematics (e.g. ergodic theory, measure theory, topological group theory, algebraic geometry, spectral theory, etc.) work best when applied to continuous (or “infinitary”) mathematical objects: real or complex numbers, manifolds, algebraic varieties, continuous topological or metric spaces, etc. In order to apply results and ideas from continuous mathematics to discrete settings, there are basically two approaches. One is to directly discretise the arguments used in continuous mathematics, which often requires one to keep careful track of all the bounds on various quantities of interest, particularly with regard to various error terms arising from discretisation which would otherwise have been negligible in the continuous setting. The other is to construct continuous objects as limits of sequences of discrete objects of interest, so that results from continuous mathematics may be applied (often as a “black box”) to the continuous limit, which then can be used to deduce consequences for the original discrete objects which are quantitative (though often ineffectively so). The latter approach is the focus of this current talk.

The following table gives some examples of a discrete theory and its continuous counterpart, together with a limiting procedure that might be used to pass from the former to the latter:

(Discrete)	(Continuous)	(Limit method)
Ramsey theory	Topological dynamics	Compactness
Density Ramsey theory	Ergodic theory	Furstenberg correspondence principle
Graph/hypergraph regularity	Measure theory	Graph limits
Polynomial regularity	Linear algebra	Ultralimits
Structural decompositions	Hilbert space geometry	Ultralimits
Fourier analysis	Spectral theory	Direct and inverse limits
Quantitative algebraic geometry	Algebraic geometry	Schemes
Discrete metric spaces	Continuous metric spaces	Gromov-Hausdorff limits
Approximate group theory	Topological group theory	Model theory

As the above table illustrates, there are a variety of different ways to form a limiting continuous object. Roughly speaking, one can divide limits into three categories:

Topological and metric limits. These notions of limits are commonly used by analysts. Here, one starts with a sequence (or perhaps a net) of objects ${x_n}$ in a common space ${X}$ , which one then endows with the structure of a topological space or a metric space, by defining a notion of distance between two points of the space, or a notion of open neighbourhoods or open sets in the space. Provided that the sequence or net is convergent, this produces a limit object ${\lim_{n \rightarrow \infty} x_n}$ , which remains in the same space, and is “close” to many of the original objects ${x_n}$ with respect to the given metric or topology.
Categorical limits. These notions of limits are commonly used by algebraists. Here, one starts with a sequence (or more generally, a diagram) of objects ${x_n}$ in a category ${X}$ , which are connected to each other by various morphisms. If the ambient category is well-behaved, one can then form the direct limit ${\varinjlim x_n}$ or the inverse limit ${\varprojlim x_n}$ of these objects, which is another object in the same category ${X}$ , and is connected to the original objects ${x_n}$ by various morphisms.
Logical limits. These notions of limits are commonly used by model theorists. Here, one starts with a sequence of objects ${x_{\bf n}}$ or of spaces ${X_{\bf n}}$ , each of which is (a component of) a model for given (first-order) mathematical language (e.g. if one is working in the language of groups, ${X_{\bf n}}$ might be groups and ${x_{\bf n}}$ might be elements of these groups). By using devices such as the ultraproduct construction, or the compactness theorem in logic, one can then create a new object ${\lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ or a new space ${\prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ , which is still a model of the same language (e.g. if the spaces ${X_{\bf n}}$ were all groups, then the limiting space ${\prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ will also be a group), and is “close” to the original objects or spaces in the sense that any assertion (in the given language) that is true for the limiting object or space, will also be true for many of the original objects or spaces, and conversely. (For instance, if ${\prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ is an abelian group, then the ${X_{\bf n}}$ will also be abelian groups for many ${{\bf n}}$ .)

The purpose of this talk is to highlight the third type of limit, and specifically the ultraproduct construction, as being a “universal” limiting procedure that can be used to replace most of the limits previously mentioned. Unlike the topological or metric limits, one does not need the original objects ${x_{\bf n}}$ to all lie in a common space ${X}$ in order to form an ultralimit ${\lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ ; they are permitted to lie in different spaces ${X_{\bf n}}$ ; this is more natural in many discrete contexts, e.g. when considering graphs on ${{\bf n}}$ vertices in the limit when ${{\bf n}}$ goes to infinity. Also, no convergence properties on the ${x_{\bf n}}$ are required in order for the ultralimit to exist. Similarly, ultraproduct limits differ from categorical limits in that no morphisms between the various spaces ${X_{\bf n}}$ involved are required in order to construct the ultraproduct.

With so few requirements on the objects ${x_{\bf n}}$ or spaces ${X_{\bf n}}$ , the ultraproduct construction is necessarily a very “soft” one. Nevertheless, the construction has two very useful properties which make it particularly useful for the purpose of extracting good continuous limit objects out of a sequence of discrete objects. First of all, there is Łos’s theorem, which roughly speaking asserts that any first-order sentence which is asymptotically obeyed by the ${x_{\bf n}}$ , will be exactly obeyed by the limit object ${\lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ ; in particular, one can often take a discrete sequence of “partial counterexamples” to some assertion, and produce a continuous “complete counterexample” that same assertion via an ultraproduct construction; taking the contrapositives, one can often then establish a rigorous equivalence between a quantitative discrete statement and its qualitative continuous counterpart. Secondly, there is the countable saturation property that ultraproducts automatically enjoy, which is a property closely analogous to that of compactness in topological spaces, and can often be used to ensure that the continuous objects produced by ultraproduct methods are “complete” or “compact” in various senses, which is particularly useful in being able to upgrade qualitative (or “pointwise”) bounds to quantitative (or “uniform”) bounds, more or less “for free”, thus reducing significantly the burden of “epsilon management” (although the price one pays for this is that one needs to pay attention to which mathematical objects of study are “standard” and which are “nonstandard”). To achieve this compactness or completeness, one sometimes has to restrict to the “bounded” portion of the ultraproduct, and it is often also convenient to quotient out the “infinitesimal” portion in order to complement these compactness properties with a matching “Hausdorff” property, thus creating familiar examples of continuous spaces, such as locally compact Hausdorff spaces.

Ultraproducts are not the only logical limit in the model theorist’s toolbox, but they are one of the simplest to set up and use, and already suffice for many of the applications of logical limits outside of model theory. In this post, I will set out the basic theory of these ultraproducts, and illustrate how they can be used to pass between discrete and continuous theories in each of the examples listed in the above table.

Apart from the initial “one-time cost” of setting up the ultraproduct machinery, the main loss one incurs when using ultraproduct methods is that it becomes very difficult to extract explicit quantitative bounds from results that are proven by transferring qualitative continuous results to the discrete setting via ultraproducts. However, in many cases (particularly those involving regularity-type lemmas) the bounds are already of tower-exponential type or worse, and there is arguably not much to be lost by abandoning the explicit quantitative bounds altogether.

— 1. Basic theory —

To set up the machinery of ultraproducts (and nonstandard analysis) we will need to pick a non-principal ultrafilter ${\alpha \in \beta {\bf N} \backslash {\bf N}}$ on the natural numbers ${{\bf N} = \{1,2,\ldots\}}$ . By definition, this is a collection ${\alpha}$ of subsets of the natural numbers ${{\bf N}}$ that obeys the following axioms:

(i) ${\alpha}$ contains ${{\bf N}}$ , but does not contain ${\emptyset}$ .
(ii) If ${A \subset {\bf N}}$ is in ${\alpha}$ , then any subset of ${{\bf N}}$ containing ${A}$ is in ${\alpha}$ .
(iii) If ${A, B}$ lie in ${\alpha}$ , then ${A \cap B}$ also lies in ${\alpha}$ .
(iv) If ${A \subset {\bf N}}$ , then exactly one of ${A}$ and ${{\bf N} \backslash A}$ lies in ${\alpha}$ .
(v) No finite set lies in ${\alpha}$ .

A collection that obeys axioms (i)-(iii) is a filter, a collection that obeys (i)-(iv) is an ultrafilter, and a collection that obeys (i)-(v) is a non-principal ultrafilter. (One can certainly build ultrafilters on other sets than the natural numbers ${{\bf N}}$ , but for the type of applications we have in mind, ultrafilters on ${{\bf N}}$ are generally sufficient, much as how one can largely rely on sequences ${(x_n)_{n \in {\bf N}}}$ instead of nets ${(x_a)_{a \in A}}$ when using considering topological or metric notions of a limit in concrete applications.)

If ${\alpha}$ is an ultrafilter, a subset ${A}$ of ${{\bf N}}$ is said to be ${\alpha}$ -large if it lies in ${\alpha}$ , and ${\alpha}$ -small otherwise. To emphasise the limit interpretation of ultrafilters, we will also use “for ${n}$ sufficiently close to ${\alpha}$ ” as a synonym for “for an ${\alpha}$ -large set of ${n}$ “. Note from the above axioms that if ${{\bf N}}$ is partitioned into finitely many components, then exactly one of these components is ${\alpha}$ -large. One can thus think of an ultrafilter as a voting protocol, which converts the preferences of a countably infinite number of voters (indexed by the natural numbers) amongst a finite number of candidates into a “winner”, namely the candidate who amasses an ${\alpha}$ -large set of votes; this voting protocol obeys all the hypotheses of Arrow’s theorem (rationality, independence of irrelevant alternatives, etc.) but not its conclusion (there are no dictators), due to the infinite number of voters. One can also view an ultrafilter as a finitely additive, ${\{0,1\}}$ -valued probability measure on the natural numbers, in which every subset of ${{\bf N}}$ is measurable.

Every natural number ${n}$ defines a principal ultrafilter ${\bar{n}}$ (that is, an ultrafilter that does not obey axiom (v)), defined by setting ${A \in \bar{n}}$ if and only if ${n \in A}$ . By abuse of notation, we may identify ${\bar{n}}$ with ${n}$ , so that the set of principal ultrafilters is identified with ${{\bf N}}$ . The set of all ultrafilters (principal and non-principal) is denoted ${\beta {\bf N}}$ , and may be identified with the Stone-Cech compactification of the natural numbers; this space has a number of interesting structures on it (for instance, it is a left-continuous topological semigroup, which is a useful fact in Ramsey theory and topological dynamics, as discussed in this previous post), but we will not discuss these structures further here. In particular, the use of ultrafilters in establishing correspondence principles between discrete and continuous structures is unrelated to the use of ultrafilters (particularly minimal or idempotent ultrafilters) in Ramsey theory and topological dynamics that is discussed in that previous post. (However, it is certainly possible to use both types of ultrafilters in separate places for a single application; see this paper of Bergelson and myself for an example.)

The existence of a non-principal ultrafilter ${\alpha}$ can be guaranteed by an application of Zorn’s lemma (basically by running the transfinite version of a greedy algorithm to build the collection of ${\alpha}$ -large and ${\alpha}$ -small sets):

Lemma 1 There exists a non-principal ultrafilter ${\alpha \in \beta {\bf N} \backslash {\bf N}}$ .

Proof: Define the Frechet filter ${F}$ to be the collection of all the cofinite subsets of ${{\bf N}}$ , that is to say those subsets of ${{\bf N}}$ whose complement is finite. This is a filter. A routine application of Zorn’s lemma shows that this filter must be contained in at least one maximal filter ${\alpha}$ . If ${\alpha}$ is not an ultrafilter, then there is a set ${E}$ which is neither ${\alpha}$ -large or ${\alpha}$ -small; if we then let ${\alpha'}$ be the filter generated by ${\alpha}$ and ${E}$ (that is, ${\alpha'}$ consists of those subsets of ${{\bf N}}$ that either lie in ${\alpha}$ , or contain the intersection of ${E}$ with an ${\alpha}$ -large set), then one checks that ${\alpha'}$ is a filter that is strictly larger than ${\alpha}$ , contradicting the maximality of ${\alpha}$ . Thus ${\alpha}$ is an ultrafilter; since it contains ${F}$ , it is non-principal as required. $\Box$

Remark 1 The above argument relied upon the axiom of choice. One can construct ultrafilters using slightly weaker set-theoretic axioms than the axiom of choice (e.g. the Boolean prime ideal theorem), but if one has no choice-like axioms whatsoever (or more precisely, one uses just the axioms ZF of Zermelo-Fraenkel set theory) then the existence of non-principal ultrafilters is undecidable. However, there is a result of Gödel that asserts that if a result is finitary in the sense that it can be phrased as a first-order statement in Peano Arithmetic, and it can be proven using the axiom of choice (or more precisely in ZFC set theory), then it can also be proven without the axiom of choice (i.e. in ZF set theory). In practical terms, this means that one can ignore the reliance on the axiom of choice for any finitary application of ultraproduct methods. Alternatively, instead of using Zorn’s lemma to construct a genuine ultrafilter, it is often possible (though messy) to build some sort of “partial” or “incomplete” ultrafilter which is still close enough to an ultrafilter to prove a desired result, but which does not need the full strength of the axiom of choice to construct. We will not discuss such methods here, but see e.g. this paper of Palmgren. (See also this previous blog post for a “cheap” version of nonstandard analysis which uses the Frechet filter rather than an ultrafilter.) In any event, we will freely rely on the axiom of choice in the rest of this post.

Henceforth, we select a single non-principal ultrafilter ${\alpha \in \beta {\bf N} \backslash {\bf N}}$ to use in the rest of the post. The choice of this ultrafilter is highly non-unique ( ${\beta {\bf N} \backslash {\bf N}}$ is uncountable), but for the purposes of establishing a correspondence between discrete and continuous mathematics, the precise choice of ultrafilter ${\alpha}$ will not be relevant, as long as it is kept fixed throughout the discussion.

We can use the ultrafilter ${\alpha}$ to form limits of sequences ${(x_{\bf n})_{{\bf n} \in {\bf N}}}$ , even if these sequences have no limit in the topological or metric senses. For instance, if ${x_{\bf n} \in X}$ takes values in a single finite space ${X}$ for all natural numbers ${{\bf n}}$ , then we can define the ultralimit to be the unique element ${x_\alpha = \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ of ${X}$ such that ${x_{\bf n} = x_\alpha}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ ; this element exists and is unique by the ultrafilter axioms (i)-(iv). For instance, the ultralimit ${(-1)^\alpha := \lim_{{\bf n} \rightarrow \alpha} (-1)^{\bf n}}$ of the sequence ${1,-1,1,-1,\ldots}$ is either ${1}$ or ${-1}$ , with the former occurring if the even numbers are ${\alpha}$ -large, and the latter occurring if the odd numbers are ${\alpha}$ -large. So the ultralimit here depends on ${\alpha}$ , but once ${\alpha}$ is fixed, the ultralimit is well-defined. One can also view ${x_\alpha = \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ as the outcome of an “election” among candidates in ${X}$ , in which each “voter” ${{\bf n}}$ has ${x_{\bf n}}$ as a preferred candidate, and the ultrafilter ${\alpha}$ is used as the election protocol. (See this previous post for further discussion of this viewpoint.)

Now we consider the more general situation in which the ${x_{\bf n}}$ to not lie in a single finite space ${X}$ , but instead each ${x_{\bf n}}$ lies in a space ${X_{\bf n}}$ which may depend on ${{\bf n}}$ , and may also be infinite. Here, there does not necessarily exist a single object ${x_\alpha}$ that is equal to the ${x_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ . The situation here is similar to that in metric spaces, in that a Cauchy sequence in a metric space ${X = (X,d)}$ need not be convergent if the space ${X}$ is infinite. In the latter case, the problem can be resolved by constructing the metric completion ${\overline{X}}$ of ${X}$ , which can be defined (slightly non-rigorously) as the space of formal limits ${\lim_{n \rightarrow \infty} x_n}$ of Cauchy sequences ${x_n}$ , with two formal limits ${\lim_{n \rightarrow \infty} x_n}$ , ${\lim_{n \rightarrow \infty} y_n}$ declared to be equal if ${d(x_n,y_n)}$ converges to zero (in the classical sense) as ${n \rightarrow \infty}$ . To construct this Cauchy completion rigorous within the framework of set theory, one can define ${\overline{X}}$ to be the set of equivalence classes of tuples ${(x_n)_{n \in {\bf N}}}$ of Cauchy sequences in ${X}$ , with the equivalence relation ${(x_n)_{n \in {\bf N}} \sim (y_n)_{n \in {\bf N}}}$ holding if and only if ${d(x_n,y_n)}$ converges to zero as ${n \rightarrow \infty}$ . In order to view ${X}$ as a subset of its completion ${\overline{X}}$ , one usually identifies each point ${x \in X}$ with the equivalence class of the corresponding constant sequence ${(x)_{n \in {\bf N}}}$ . With this construction, one can for instance build the real numbers ${{\bf R}}$ as the metric completion of the rationals ${{\bf Q}}$ (and this is indeed one of the most popular ways to construct the reals, which is often covered in undergraduate analysis classes). Note though while one can use this set-theoretic machinery of equivalence classes of Cauchy sequences of rationals to construct the reals, for the purposes of using the real numbers ${{\bf R}}$ for mathematical applications, this set-theoretic construction is not relevant; the only thing one needs to retain is that Cauchy sequences of rationals (or of reals) will converge to a real, and conversely every real is the limit of a Cauchy sequence of rationals.

We can take a similar tack to construct ultralimits ${\lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ of sequences ${x_{\bf n} \in X_{\bf n}}$ in different spaces ${X_{\bf n}}$ . If one is willing to be slightly non-rigorous, the definition is almost the same: we can view these ultralimits as formal objects, with two ultralimits ${\lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ and ${\lim_{{\bf n} \rightarrow \alpha} y_{\bf n}}$ declared to be equal if and only if ${x_{\bf n}=y_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ . To do things rigorously within the framework of set theory, one has to take a little extra care to avoid the set-theoretic issues associated to Russell’s paradox (or more precisely, avoiding the uses of proper classes that are too large to be sets). One way to deal with this is as follows. One can postulate the existence of a standard universe ${{\mathfrak U}}$ that contains all the objects of interest for one’s particular mathematical problem: for instance, if one is interested in a sequence of groups ${G_{\bf n}}$ , then ${{\mathfrak U}}$ might contain all the elements of all of the ${G_{\bf n}}$ . The only requirements we make of this standard universe are that (a) it is a set (rather than a proper class), and (b) it is fixed throughout the mathematical discussion. The former requirement means that ${{\mathcal U}}$ , in general, cannot contain all spaces of a particular type; for instance, one cannot make ${{\mathcal U}}$ contain all groups, all vector spaces, all graphs, etc., as one would soon run into Russell-type paradoxes if this occurred. However, in practice, for any given mathematical problem (other than those arising within mathematical logic), one usually does not need to work simultaneously with all spaces; usually a much smaller number of spaces, e.g. a countable or uncountable family of such spaces, will suffice. Henceforth we will take the existence of a standard universe ${{\mathfrak U}}$ for granted. Elements of this universe will be referred to as standard objects, and subsets of the universe as standard spaces; for instance, we will usually place the classical number systems ${{\bf N}, {\bf Z}, {\bf R}}$ , etc. inside this standard universe, so elements of ${{\bf N}}$ become standard natural numbers, elements of ${{\bf R}}$ become standard reals, and so forth. We then have:

Definition 2 (Formal definition of ultralimits and ultraproducts) Let ${(x_{\bf n})_{{\bf n} \in E}}$ be a sequence of standard objects, defined for an ${\alpha}$ -large set ${E}$ (thus ${x_{\bf n} \in {\mathfrak U}}$ for all ${n \in E}$ ). The ultralimit ${x_\alpha = \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ is then defined to be the equivalence class of tuples ${(y_{\bf n})_{{\bf n} \in E'}}$ of standard objects defined on an ${\alpha}$ -large set ${E'}$ , such that ${x_{\bf n} = y_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ in the common domain ${E \cap E'}$ of definition. Such an ultralimit is called a nonstandard object, and the set of all ultralimits is called the nonstandard universe ${{}^* {\mathfrak U}}$ . We identify every standard object ${x}$ with the nonstandard object ${\lim_{{\bf n} \rightarrow \alpha} x}$ , thus embedding ${{\mathfrak U}}$ in ${{}^* {\mathfrak U}}$ .

Given a sequence ${X_{\bf n}}$ of standard spaces (i.e. subsets of ${{\mathfrak U}}$ ) defined for ${{\bf n}}$ sufficiently close to ${\alpha}$ , the ultraproduct ${X_\alpha = \prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ is defined as the set of all ultralimits ${\lim_{{\bf n} \rightarrow\alpha} x_{\bf n}}$ , where ${x_{\bf n}}$ lies in ${X_{\bf n}}$ for an ${\alpha}$ -large set of ${n}$ . Such an ultraproduct (which is a subset of ${{}^* {\mathfrak U}}$ ) will be called a nonstandard space (also known as an internal space). Similarly, the ultraproduct of a sequence of standard groups will be called a nonstandard group (or internal group), the ultraproduct of a sequence of standard fields will be called a nonstandard field (or internal field), and so forth.

If ${X}$ is a standard space, the nonstandard space ${\prod_{{\bf n} \rightarrow\alpha} X}$ (that is, the space of ultralimits of sequences in ${X}$ ) will be called the ultrapower of ${X}$ and is denoted ${{}^* X}$ ; note that ${X}$ embeds as a subset of ${{}^* X}$ . The ultrapower ${{}^* {\bf N}}$ of the standard natural numbers will be referred to as the nonstandard natural numbers, the ultrapower ${{}^* {\bf R}}$ of the standard reals will be referred to as the nonstandard real numbers (also known as the umber), and so forth.

One can verify that when ${X}$ is finite, the ultrapower ${{}^* X}$ is equal to ${X}$ itself, and that the notion of an ultralimit ${\lim_{{\bf n} \rightarrow\alpha} x_{\bf n}}$ in the case when all the ${x_{\bf n}}$ lie in ${X}$ corresponds to the notion of an ultralimit defined previously.

The basic ontological Venn diagram is this: the standard universe ${{\mathfrak U}}$ embeds into the larger nonstandard universe ${{}^* {\mathfrak U}}$ , and both exist inside the even larger “external universe” of ZFC set theory, which we will not give a name to (it is not a set, but is instead a proper class). This allows us to study various mathematical objects on three different levels: standard, nonstandard, and external. For instance, we have standard groups (groups in ${{\mathfrak U}}$ ) and nonstandard groups (ultraproducts of groups in ${{\mathfrak U}}$ ); both are examples of external groups (groups that are somewhere in the external universe), but there are certainly examples of external groups that are neither standard groups nor nonstandard groups. It is also worth cautioning that while we identify standard objects ${x}$ with their nonstandard counterparts ${\lim_{{\bf n} \rightarrow\alpha} x}$ , we do not identify standard spaces ${X}$ with their nonstandard counterparts ${{}^* X = \prod_{{\bf n} \rightarrow\alpha} X}$ ; in particular, we do not view standard groups as examples of nonstandard groups (except in the finite case), nor do we view standard fields as examples of nonstandard fields, etc. Instead, one can view the nonstandard space ${{}^* X}$ as a “completion” of the standard space ${X}$ , analogous to metric completion; see this previous blog post for further discussion of this perspective. A related perspective is to view ${{}^* X}$ as a double-precision version of ${X}$ , so for instance ${{}^* {\bf R}}$ can be viewed as the space of “double-precision real numbers” as opposed to the “single-precision” real numbers in ${{\bf R}}$ , or similarly ${{}^* {\bf Z}}$ may be viewed as a space of “long integers“, with ${{\bf Z}}$ being a space of “short integers”.

The analogues of standard groups, nonstandard groups, and external groups in finitary mathematics would be “groups ${G}$ that do not depend on an asymptotic parameter ${n}$ “, “groups ${G_{\bf n}}$ that may depend on an asymptotic parameter ${{\bf n}}$ “, and “informal group-like objects (such as the “group” of all “bounded” integers ${m = O(1)}$ ) that may require asymptotic notation to define” respectively. The latter concept is hard to pin down rigorously in finitary mathematics, even though the intuition it captures (e.g. that the “set” of “bounded” integers should be closed under addition) is fairly clear; but once one uses ultraproducts to separate the three levels of standard, nonstandard, and external objects, it is possible to make rigorous sense of these sorts of intuitions, as we shall see later.

Given a sequence ${f_{\bf n}: X_{\bf n} \rightarrow Y_{\bf n}}$ of standard functions between standard sets ${X_{\bf n},Y_{\bf n}}$ for an ${\alpha}$ -large set of ${n}$ , we define the ultralimit ${f_\alpha = \lim_{{\bf n} \rightarrow\alpha} f_{\bf n}}$ of this sequence to be the function ${f_\alpha: X_\alpha \rightarrow Y_\alpha}$ from the nonstandard space ${X_\alpha := \prod_{{\bf n} \rightarrow\alpha} X_{\bf n}}$ to the nonstandard space ${Y_\alpha := \prod_{{\bf n} \rightarrow\alpha} Y_{\bf n}}$ defined by the formula

$\displaystyle f_\alpha( \lim_{{\bf n} \rightarrow\alpha} x_{\bf n} ) := \lim_{{\bf n} \rightarrow\alpha} f_{\bf n}( x_{\bf n} )$

for all sequences ${x_{\bf n}}$ that lie in ${X_{\bf n}}$ for an ${\alpha}$ -large set of ${n}$ . It is easy to see that this ultralimit is well-defined; we refer to such functions as nonstandard functions.

From the above construction, we may now transfer operations and relations on standard spaces to their nonstandard counterparts. For instance, if ${G_{\bf n}}$ is a sequence of standard groups, then one can take the ultralimit of the multiplication operations ${\cdot_{\bf n}: G_{\bf n} \times G_{\bf n} \rightarrow G_{\bf n}}$ to obtain a multiplication operation ${\cdot_\alpha: G_\alpha \times G_\alpha \rightarrow G_\alpha}$ on the ultraproduct ${G_\alpha := \prod_{{\bf n} \rightarrow\alpha} G_{\bf n}}$ ; similarly, the inversion operation on ${G_{\bf n}}$ gives rise to an inversion operation on ${G_\alpha}$ . Similarly, the arithmetic operations on the standard natural numbers ${{\bf N}}$ can be transferred to arithmetic operations on the nonstandard natural numbers ${{}^* {\bf N}}$ , and properties and relations on the natural numbers can similarly be transferred. For instance, a nonstandard number ${N = \lim_{{\bf n} \rightarrow\alpha} N_{\bf n}}$ can be said to be prime if the ${N_{\bf n}}$ are prime for an ${\alpha}$ -large set of ${n}$ (i.e. the ultralimit of the truth value of “ ${N_{\bf n}}$ is prime” is true); one nonstandard number ${N = \lim_{{\bf n} \rightarrow\alpha} N_{\bf n}}$ can be said to be larger than another ${M = \lim_{{\bf n} \rightarrow\alpha} M_{\bf n}}$ if one has ${N_{\bf n} > M_{\bf n}}$ for an ${\alpha}$ -large set of ${n}$ ; and so forth.

One can then check by hand that statements that are true for standard objects are also true for their nonstandard counterparts. For instance, because the group operations of the standard groups ${G_{\bf n}}$ are associative, the group operation on the nonstandard group ${G_\alpha}$ is also associative, and in fact ${G_\alpha}$ will also be a group (as viewed externally). Similarly, addition and multiplication in the nonstandard natural numbers ${{}^* {\bf N}}$ obey the usual commutative, associative, and distributive laws, because these transfer from the corresponding laws for the standard natural numbers ${{\bf N}}$ . For a more topical example, it is now a theorem that given any standard natural number ${N}$ , there exist standard primes ${p,q}$ such that ${N < p < q \leq p+600}$ ; it is an instructive exercise to check that the same result then automatically holds in the nonstandard setting, thus for every nonstandard natural number ${N}$ there exist nonstandard primes ${p,q}$ such that ${N < p < q \leq p+600}$ .

These facts are special cases of the transfer principle, and can be formalised by Łos’s theorem. Informally, this theorem asserts that if an “elementary” sentence holds for (an ${\alpha}$ -large subsequence of) a sequence of standard objects, then it also holds in the ultralimit, and conversely. To make this assertion rigorous, we need some of the notation from first-order logic; this is somewhat formal and the reader may wish to skim briefly over the definitions and proofs that follow. To simplify the discussion, we restrict attention to one-sorted languages, although in practice one often works with many-sorted languages instead.

Definition 3 (Languages and structures, formal definition) A signature is a collection of formal operation symbols ${O}$ and relation symbols ${R}$ , each of which is assigned an arity ${k}$ (a non-negative integer). (For instance, the signature of the language of groups would consist of the ${2}$ -ary operation ${\cdot}$ , the ${1}$ -ary operation ${()^{-1}}$ , and the ${0}$ -ary operation ${1}$ .) ${0}$ -ary operations are also known as constant symbols. Given a signature and an infinite supply of variable symbols ${x}$ , define a term to be a formal string generated by the following rules:

Every variable symbol ${x}$ is a term.

If ${O}$ is a ${k}$ -ary operation and ${z_1,\ldots,z_k}$ are terms, then ${O( z_1,\ldots,z_k )}$ is a term.

By abuse of notation, we often move operation symbols to more traditional locations, for instance writing ${+(x,y)}$ as ${(x+y)}$ , ${\cdot(x,y)}$ as ${(x \cdot y)}$ , etc.. By further abuse of notation, parentheses are usually omitted when there is no loss of ambiguity, e.g. ${(x+y)}$ is often abbreviated as ${x+y}$ .

A formula ${\phi(x_1,\ldots,x_m)}$ involving some finite number of distinct variable symbols ${x_1,\ldots,x_m}$ (known as the free variables of the formula) for some ${m \geq 0}$ is then a formal string generated by the following rules:

If ${R}$ is a ${k}$ -ary relation and ${z_1,\ldots,z_k}$ are terms which only involve variables from ${x_1,\ldots,x_m}$ , then ${R(z_1,\ldots,z_k)}$ is a formula of ${x_1,\ldots,x_m}$ .

If ${z, z'}$ are terms only involving variables from ${x_1,\ldots,x_m}$ , then ${(z=z')}$ is a formula with free variables ${x_1,\ldots,x_m}$ .

If ${\varphi = \varphi(x_1,\ldots,x_{\bf n}), \psi = \psi(x_1,\ldots,x_m)}$ are formulae with free variables ${x_1,\ldots,x_m}$ , then ${(\neg \varphi), (\varphi \wedge \psi), (\varphi \vee \psi), (\varphi \implies \psi)}$ , and ${(\varphi \iff \psi)}$ are formulae with free variables ${x_1,\ldots,x_m}$ .

If ${\varphi = \varphi(x_1,\ldots,x_m,x)}$ is a formula with free variables ${x_1,\ldots,x_m,x}$ (or some permutation thereof), then ${(\forall x: \varphi)}$ and ${(\exists x: \varphi)}$ are formulae with free variables ${x_1,\ldots,x_m}$ .

A formula with no free variables is known as a sentence. As before, we abuse notation by moving relation symbols to more traditional locations, e.g. writing ${<(x,y)}$ as ${(x < y)}$ , and by removing parentheses whenever there is no loss of ambiguity; we also permit concatenation of quantifiers, for instance abbreviating ${(\forall x: (\forall y: \varphi(x,y)))}$ as ${\forall x,y: \varphi(x,y)}$ . Thus, for instance, in the language of the natural numbers,

$\displaystyle \exists p,q: n = p+q \wedge \neg (\exists a,b > 1: p=ab) \wedge \neg (\exists c,d > 1: q=cd)$

is a formula of one variable ${n}$ , and

$\displaystyle \forall n > 2: (\exists m: n=2m) \implies$

$\displaystyle (\exists p,q: n = p+q \wedge \neg (\exists a,b > 1: p=ab) \wedge \neg (\exists c,d > 1: q=cd))$

is a sentence (which, in this case, encodes the even Goldbach conjecture).

We refer to the collection ${{\mathcal L}}$ of such formulae as the first-order language (or language, for short) associated with the given signature (and to the supply of variable symbols).

A structure ${M}$ for a first-order language ${{\mathcal L}}$ is a set ${M}$ , together with a map ${O_M: M^k \rightarrow M}$ for every ${k}$ -ary operation ${O}$ , and a boolean relation ${R_M: M^k \rightarrow \{\hbox{true}, \hbox{false}\}}$ for every ${k}$ -ary relation ${R}$ . (For instance, a group is a structure for the first-order language of groups.) Any term ${z}$ of ${n}$ variables ${x_1,\ldots,x_{\bf n}}$ may be interpreted as a function ${z_M: M^{\bf n} \rightarrow M}$ by viewing the variable symbols ${x_1,\ldots,x_{\bf n}}$ as ranging in ${M}$ , and replacing each operation ${O}$ or relation ${R}$ with their respective interpretations ${O_k, R_k}$ . Similarly, any formula ${\phi(x_1,\ldots,x_{\bf n})}$ may be interpreted as a function ${\phi_M: M^{\bf n} \rightarrow\{\hbox{true}, \hbox{false}\}}$ , and in particular any sentence ${\phi}$ is interpreted to be either true or false (and we write ${M \models \phi}$ if the former occurs), by interpreting quantifiers such as ${\forall x}$ and ${\exists x}$ as quantification over ${M}$ . (For instance, ${\exists x: \phi(x,y)}$ is interpreted as true for ${y \in M}$ if there exists ${x \in M}$ such that ${\phi_M(x,y)}$ is true.)

Given a sequence ${M_{\bf n}}$ of standard structures for a given first-order language ${{\mathcal L}}$ , we can form the ultraproduct ${M_\alpha := \prod_{{\bf n} \rightarrow\alpha} M_{\bf n}}$ in the obvious manner, with the nonstandard interpretations ${O_{M_\alpha}, R_{M_\alpha}}$ of the operator and relation symbols ${O,R}$ being the ultralimits of their standard counterparts. We refer to this ultraproduct as a nonstandard structure for the first-order language ${{\mathcal L}}$ ; both standard structures and nonstandard structures are examples of external structures, but as remarked before we do not consider standard structures as examples of nonstandard structures (except when the structure is finite).

Theorem 4 (Łos’s theorem) Let ${M_{\bf n}}$ be a sequence of standard structures for a first-order language ${{\mathcal L}}$ , and let ${M_\alpha = \prod_{{\bf n} \rightarrow\alpha} M_{\bf n}}$ be the associated nonstandard structure.

(i) If ${z}$ is a term involving the variables ${x_1,\ldots,x_m}$ , then ${z_{M_\alpha}: M_\alpha^m\rightarrow M_\alpha}$ is the ultralimit of the ${z_{M_{\bf n}}: M_{\bf n}^m \rightarrow M_{\bf n}}$ .

(ii) If ${\phi(x_1,\ldots,x_m)}$ is a formula with free variables ${x_1,\ldots,x_m}$ , then ${\phi_{M_\alpha}: M_\alpha^m \rightarrow \{ \hbox{true}, \hbox{false} \}}$ is the ultralimit of ${\phi_{M_{\bf n}}: M_{\bf n}^m \rightarrow \{ \hbox{true}, \hbox{false} \}}$ .

(iii) If ${\phi}$ is a sentence, then ${M_\alpha \models \phi}$ is true if and only if ${M_{\bf n} \models \phi}$ is true for ${{\bf n}}$ sufficiently close to ${\alpha}$ .

Informally, this theorem asserts that first-order logic is continuous with respect to ultralimits.

Proof: The claim (i) is obtained by a routine induction on the length of the term ${z}$ and the ultrafilter axioms, while the claim (iii) is a consequence of (ii). The claim (ii) is similarly obtained by a routine induction on the length of the formula ${\phi}$ and the ultrafilter axioms; the only non-trivial claim to verify is that if the formula ${(x_1,\ldots,x_m,x) \mapsto \phi_{M_\alpha}(x_1,\ldots,x_m,x)}$ is the ultralimit of the formulae ${(x_1,\ldots,x_m,x) \mapsto \phi_{M_{\bf n}}(x_1,\ldots,x_m,x)}$ , then the formula ${(x_1,\ldots,x_m) \mapsto \exists x \in M_\alpha: \phi_{M_\alpha}(x_1,\ldots,x_m,x)}$ is the ultralimit of the formulae ${(x_1,\ldots,x_m) \mapsto \exists x \in M_{\bf n}: \phi_{M_{\bf n}}(x_1,\ldots,x_m,x)}$ , and similarly for the universal quantifier ${\forall}$ .

We just prove the claim for the existential quantifier ${\exists}$ , as the claim for ${\forall}$ is similar (and can be deduced from the existential case by rewriting ${\forall x:\phi}$ in the equivalent form ${\neg( \exists x: \neg \phi) )}$ . Suppose first that ${x_{i,\alpha} = \lim_{{\bf n} \rightarrow \alpha} x_{i,{\bf n}} \in M_\alpha}$ for ${i=1,\ldots,k}$ are such that ${\exists x_{\bf n} \in M_{\bf n}: \phi_{M_{\bf n}}(x_{1,{\bf n}},\ldots,x_{m,{\bf n}},x_{\bf n})}$ holds for ${{\bf n}}$ sufficiently close to ${\alpha}$ ; by the axiom of choice, we may thus find ${x_{\bf n} \in M_{\bf n}}$ such that ${\phi_{M_{\bf n}}(x_{1,{\bf n}},\ldots,x_{m,{\bf n}},x_{\bf n})}$ holds for ${{\bf n}}$ sufficiently close to ${\alpha}$ . Taking ultralimits and using the induction hypothesis, we conclude that ${\phi_{M_{\alpha}}(x_{1,{\alpha}},\ldots,x_{m,{\alpha}},x_{\alpha})}$ where ${x_\alpha := \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ , so that ${\exists x \in M_\alpha: \phi_{M_\alpha}(x_{1,\alpha},\ldots,x_{m,\alpha},x_\alpha)}$ is true. Conversely, suppose that ${\exists x_{\bf n} \in M_{\bf n}: \phi_{M_\alpha}(x_{1,{\bf n}},\ldots,x_{m, {\bf n}},x_{\bf n})}$ fails for ${{\bf n}}$ sufficiently close to ${\alpha}$ ; then for any ${x_\alpha = \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ in ${M_\alpha}$ , ${\phi_{M_{\bf n}}(x_{1,{\bf n}},\ldots,x_{m, {\bf n}},x_{\bf n})}$ fails for ${{\bf n}}$ sufficiently close to ${\alpha}$ , and hence on taking ultralimits ${\phi_{M_{\alpha}}(x_{1,{\alpha}},\ldots,x_{m, {\alpha}},x_{\alpha})}$ fails also, and the claim follows. $\Box$

We now give a classic consequence of Łos’s theorem to logic, namely the countable case of the compactness theorem:

Corollary 5 (Compactness theorem, countable case) Let ${{\mathcal L}}$ be a first-order language, and let ${\phi_1, \phi_2, \ldots}$ be a sequence of sentences. Suppose that for each natural number ${{\bf n}}$ , there exists a structure ${M_{\bf n}}$ for ${{\mathcal L}}$ such that ${\phi_1,\ldots,\phi_{{\bf n}}}$ are satisfied by this structure. Then there exists a structure ${M}$ such that ${\phi_1,\phi_2,\ldots}$ are simultaneously satisfied by this structure.

The general case of the compactness theorem may be established by using ultraproducts on more general sets than the natural numbers; we leave the verification of this fact to the reader.

Proof: We select the standard universe ${{\mathfrak U}}$ to contain all of the ${M_{\bf n}}$ , so that the ${M_{\bf n}}$ are all standard structures. If we then set ${M}$ to be the nonstandard structure ${\prod_{{\bf n} \rightarrow \alpha} M_{\bf n}}$ , the claim follows from Łos’s theorem. $\Box$

— 2. Rank decompositions —

We can now give a simple example of how ultralimits may be used to connect quantitative finitary statements to qualitative infinitary statements, by giving an easy case of the polyomial regularity lemma, introduced by Ben Green and myself. Given a finite-dimensional vector space ${V}$ over a field ${{\bf F}}$ and a natural number ${d}$ , we define a polynomial ${P: V \rightarrow {\bf F}}$ of degree at most ${d}$ on ${V}$ to be a function of the form

$\displaystyle P( x_1 e_1 + \ldots + x_n e_n ) = \sum_{i_1,\ldots,i_n \geq 0: i_1+\ldots+i_n \leq d} c_{i_1,\ldots,i_n} x_1^{i_1} \ldots x_n^{i_n}$

for any basis ${e_1,\ldots,e_n}$ of ${V}$ and some coefficients ${c_{i_1,\ldots,i_n} \in F}$ ; it is easy to see that the choice of basis is irrelevant for this definition. If ${V}$ is infinite dimensional instead of finite dimensional, we say that ${P: V \rightarrow F}$ is a polynomial of degree at most ${d}$ if its restriction to any finite-dimensional subspace is still a polynomial of degree at most ${d}$ . The space of such polynomials will be denoted ${\hbox{Poly}_d(V)}$ ; this is itself a vector space over ${{\bf F}}$ .

If ${P \in \hbox{Poly}_d(V)}$ for some ${d \geq 2}$ , we define the rank ${\hbox{rank}_{d-1}(P)}$ to be the least integer ${m}$ such that we can find ${Q_1,\ldots,Q_m \in \hbox{Poly}_{d-1}(V)}$ such that ${P}$ is a function of the ${Q_1,\ldots,Q_m}$ , that is to say there exists a function ${f: {\bf F}^m \rightarrow {\bf F}}$ such that ${P(x) = f(Q_1(x),\ldots,Q_m(x))}$ for all ${x \in V}$ . When ${V}$ is finite-dimensional, the rank is necessarily finite (just take ${Q_1,\ldots,Q_m}$ to be the coordinate functions), but the rank may be infinite when ${V}$ is infinite dimensional. This notion of rank is analogous to the notion of the rank of a quadratic form (which is essentially the ${d=2}$ case of the above notion).

We then have the following simple fact:

Lemma 6 (Polynomial regularity lemma) Let ${a \geq 0}$ be a non-negative integer, and let ${F: {\bf N} \rightarrow {\bf N}}$ be a function. Then there exists a constant ${C = C_{a,F}}$ with the following properties: for any ${d \geq 2}$ , any vector space ${V}$ over a field ${{\bf F}}$ , and any polynomials ${P_1,\ldots,P_a \in \hbox{Poly}_d(V)}$ , there exists polynomials ${Q_1,\ldots,Q_b \in \hbox{Poly}_d(V)}$ for some ${0 \leq b \leq a}$ and a quantity ${1 \leq M \leq C}$ with the following properties:

(i) (Representation modulo low rank) For each ${1 \leq i \leq a}$ , there exists a representation ${P_i = \sum_{j=1}^b c_{ij} Q_j + E_i}$ , where ${c_{ij} \in {\bf F}}$ and ${\hbox{rank}_{d-1}(E_i) \leq M}$ .

(ii) (Independence modulo low rank) For every ${c_1,\ldots,c_b \in {\bf F}}$ , not all zero, we have ${\hbox{rank}_{d-1}(\sum_{j=1}^b c_j Q_j) \geq F(M)}$ .

(In applications, one actually needs an iterated version of this lemma, in which the degree ${d-1}$ polynomials involved in ${E_i}$ are themselves regularised in terms of high rank or lower degree polynomials, and so on and so forth down to the linear polynomials; for simplicity we will not discuss this iterated version here, but see the above-mentioned paper of Ben and myself for more discussion.)

The standard proof of this lemma is not difficult, and can be described by the following algorithm:

(Step 0) Initialise ${a=b}$ , ${Q_j = P_j}$ for ${j=1,\ldots,b}$ , and ${M = 1}$ .
(Step 1) If property (ii) holds then STOP. Otherwise, move on to Step 2.
(Step 2) By the failure of (ii), and by permuting the ${Q_j}$ if necessary, we may write ${Q_b}$ as a linear combination of ${Q_1,\ldots,Q_{b-1}}$ , plus a polynomial of rank at most ${F(M)}$ . If we then delete ${Q_b}$ , we see that every ${P_i}$ is still a linear combination of ${Q_1,\ldots,Q_{b-1}}$ , plus an error of rank at most ${M+F(M)}$ .
(Step 3) Replace ${b}$ by ${b-1}$ (thus deleting ${Q_b}$ ), replace ${M}$ by ${M+F(M)}$ , and return to Step 1.

Since ${b}$ decreases by one at each loop of the algorithm, it loops at most ${a}$ times, and the claim follows.

The above quantitative lemma can be deduced instead from the following basic fact in linear algebra, a variant of the Steinitz exchange lemma:

Lemma 7 Let ${v_1,\ldots,v_a}$ be a finite collection of vectors in a vector space ${W}$ . Then there exists a linearly independent set of vectors ${w_1,\ldots,w_b}$ in ${W}$ for some ${b \leq a}$ such that each ${v_i}$ is a linear combination of the ${w_j}$ .

Indeed, one just sets ${w_1,\ldots,w_b}$ to be a basis of the linear span of the ${v_1,\ldots,v_a}$ . The ${w_1,\ldots,w_b}$ can also be constructed from the ${v_1,\ldots,v_a}$ by an algorithm extremely similar to the one given above; we leave this to the reader as an exercise.

From Lemma 7 we immediately obtain a qualitative version of Lemma 6:

Corollary 8 (Qualitative polynomial regularity lemma) Let ${a \geq 0}$ be a non-negative integer. Then for any ${d \geq 2}$ , any vector space ${V}$ over a field ${{\bf F}}$ , and any polynomials ${P_1,\ldots,P_a \in \hbox{Poly}_d(V)}$ , there exists polynomials ${Q_1,\ldots,Q_b \in \hbox{Poly}_d(V)}$ for some ${0 \leq b \leq a}$ with the following properties:

(i) (Representation modulo low rank) For each ${1 \leq i \leq a}$ , there exists a representation ${P_i = \sum_{j=1}^b c_{ij} Q_j + E_i}$ , where ${c_{ij} \in {\bf F}}$ and ${\hbox{rank}_{d-1}(E_i) < \infty}$ .

(ii) (Independence modulo low rank) For every ${c_1,\ldots,c_b \in {\bf F}}$ , not all zero, we have ${\hbox{rank}_{d-1}(\sum_{j=1}^b c_j Q_j) = +\infty}$ .

Proof: Let ${W}$ be the set of all polynomials in ${\hbox{Poly}_d(V)}$ of finite rank; this is clearly a subspace of ${\hbox{Poly}_d(V)}$ , so we may form the quotient space ${\hbox{Poly}_d(V)/W}$ , which is still a vector space over ${{\bf F}}$ . If we then apply Lemma 7 to the projection ${v_1,\ldots,v_a}$ of the ${P_1,\ldots,P_a}$ to this quotient space ${\hbox{Poly}_d(V)/W}$ , we obtain the claim. $\Box$

While Corollary 8 certainly looks very similar to Lemma 6, it appears at first glance that it cannot be used to prove Lemma 6, because the latter lemma has meaningful content when ${V}$ is finite-dimensional, whereas the former Corollary is trivial in that setting. However, this can be rectified by passing from the finitary setting to the infinitary setting. This can be done in a number of ways, but we will do this using the ultrafilter machinery just developed.

Proof: (Proof of Lemma 6 using Corollary 8.) We use the “compactness and contradiction” method. Suppose for contradiction that Lemma 6 failed. Carefully negating the quantifiers, and using the axiom of choice, this means that there exists ${a \geq 0}$ and ${F: {\bf N} \rightarrow {\bf N}}$ , with the property that for each ${{\bf n}}$ , we can find a vector space ${V_{\bf n}}$ over a field ${{\bf F}_{\bf n}}$ and polynomials ${P_{1,{\bf n}},\ldots,P_{a,{\bf n}} \in \hbox{Poly}_d(V_{\bf n})}$ , such that for any ${1 \leq M \leq {\bf n}}$ , there does NOT exist ${0 \leq b \leq a}$ , ${Q_{1,{\bf n}},\ldots,Q_{b,{\bf n}} \in \hbox{Poly}_d(V_{\bf n})}$ , obeying the properties (i), (ii) of Lemma 6 with the given data.

We may place all of the objects just constructed in a standard universe ${{\mathfrak U}}$ . Taking ultralimits (and using Łos’s theorem repeatedly), we obtain a nonstandard field ${{\bf F}_\alpha = \prod_{{\bf n} \rightarrow \alpha} {\bf F}_{\bf n}}$ , a nonstandard vector space ${V_\alpha = \prod_{{\bf n} \rightarrow \alpha} V_{\bf n}}$ over that field, polynomials ${P_{1,{\bf \alpha}},\ldots,P_{a,{\bf \alpha}} \in \hbox{Poly}_d(V_\alpha)}$ , with the property that for any standard integer ${M \geq 1}$ , there does NOT exist ${0 \leq b \leq a}$ , ${Q_{1,\alpha},\ldots,Q_{b,\alpha} \in \hbox{Poly}_d(V_\alpha)}$ , obeying the properties (i), (ii) of Lemma 6 with the given data. However, if one applies Corollary 8, we can find ${Q_{1,\alpha},\ldots,Q_{b,\alpha} \in \hbox{Poly}_d(V_\alpha)}$ obeying the conclusions (i), (ii) of Corollary 8. This implies the conclusions (i), (ii) of Lemma 6 if ${M}$ is chosen large enough, giving the required contradiction. $\Box$

— 3. Saturation and colouring —

Ultraproducts enjoy a very useful compactness-type property, known as countable saturation (or more precisely, ${\omega_1}$ -saturation). This property may be phrased in many ways, but we will use the following version which emphasises the analogy with topological compactness.

Let ${X}$ be a nonstandard set, thus ${X = \prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ for some standard sets ${X_{\bf n}}$ . We call an internal subset or nonstandard subset of ${X}$ to be any subset ${Y}$ of ${X}$ of the form ${Y = \prod_{{\bf n} \rightarrow \alpha} Y_{\bf n}}$ ; by Łos’s theorem we see that ${Y_{\bf n} \subset X_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ . For instance, in the nonstandard natural numbers ${{}^* {\bf N}}$ , the nonstandard intervals ${[N] := \{ n \in {}^* {\bf N}: n \leq N \}}$ are internal sets for any nonstandard natural number ${N \in {}^* {\bf N}}$ ; indeed, if ${N = \lim_{{\bf n} \rightarrow \alpha} N_n}$ , then ${[N]}$ is the ultraproduct of the standard intervals ${[N_{\bf n}]}$ . More generally, from Łos’s theorem we see that any subset of ${X}$ that is defined by a first-order predicate is an internal set. On the other hand, as we shall see later, the standard natural numbers ${{\bf N}}$ are not an internal subset of ${{}^* {\bf N}}$ (and are thus merely an external subset of ${{}^* {\bf N}}$ ).

From Łos’s theorem we see that the internal subsets of a nonstandard set ${X}$ form a boolean algebra. We then have the following compactness property:

Proposition 9 (Countable saturation) Every countable cover of ${X}$ by internal sets ${E_1,E_2,\ldots}$ has a finite subcover. Equivalently, if ${F_1,F_2,\ldots}$ are a countable sequence of internal sets such that ${F_1 \cap \ldots \cap F_M}$ is non-empty for each ${M}$ , then ${\bigcap_{m=1}^\infty F_m}$ is also non-empty.

We remark that if we had used ultraproducts on larger index sets than the natural numbers, then we would be able to obtain stronger saturation properties than countable saturation, although it is never possible to get unlimited saturation (since every point in a nonstandard set ${X}$ is an internal set). In model theoretic applications it can be technically convenient to work with an extremely saturated model (e.g. a structure which is saturated up to an inaccessible cardinal), but for most applications outside of logic and set theory, such “monster models” are not necessary, and the more modest device of ultraproducts over countable index sets is often sufficient.

Proof: It suffices to prove the second claim, as the former follows by taking complements.

Write ${F_m = \prod_{{\bf n} \rightarrow \alpha} F_{m,{\bf n}}}$ , then for each ${m}$ , ${\bigcap_{m=1}^M F_m}$ is the ultraproduct of ${\bigcap_{m=1}^M F_{m,{\bf n}}}$ . In particular, ${\bigcap_{m=1}^M F_{m,{\bf n}}}$ is non-empty for all ${{\bf n}}$ in an ${\alpha}$ -large subset ${E_M}$ of the natural numbers. By shrinking the ${E_M}$ as necessary we may assume that they are monotone, thus ${E_1 \supset E_2 \supset \ldots}$ , and such that ${E_M}$ does not contain any natural number less than ${M}$ ; in particular, ${\bigcap_{M=1}^\infty E_M = \emptyset}$ . For any ${{\bf n} \in E_1}$ , let ${M_{\bf n}}$ denote the largest natural number ${M}$ such that ${{\bf n} \in E_M}$ , and then let ${x_{\bf n}}$ denote an element of ${\bigcap_{m=1}^{M_{\bf n}} F_{m,{\bf n}}}$ . Then by construction, for each ${m \geq 1}$ , we have ${x_{\bf n} \in F_{m,{\bf n}}}$ for all ${{\bf n} \in E_m}$ , and thus the nonstandard object ${x := \lim_{{\bf n} \rightarrow \alpha} x_{\bf n}}$ lies in ${F_m}$ for all ${m}$ , and thus ${\bigcap_{m=1}^\infty F_m}$ is non-empty as required. $\Box$

This shows for instance that (as claimed previously) ${{\bf N}}$ is not an internal subset of ${{}^* {\bf N}}$ , since it can be countably covered by the singleton sets ${\{n\}}$ for ${n \in {\bf N}}$ which are internal, but for which no finite cover exists. Among other things, this establishes the overspill principle: if a nonstandard formula ${P: {}^* {\bf N} \rightarrow \{\hbox{true},\hbox{false}\}}$ holds for all standard natural numbers, then it must hold for at least one unbounded natural number (defined as a nonstandard natural number that is not a standard natural number).

Another immediate corollary of the above proposition is that if a nonstandard set ${X}$ is covered by a countable sequence ${E_1,E_2,\ldots}$ of internal subsets, then the topology ${{\mathcal F}}$ on ${X}$ generated by ${E_1,E_2,\ldots}$ is compact (because it has a countable base of internal susbets, and Proposition 9 then gives countable compactness).

As an application of this compactness observation, we use ultraproducts to illustrate the topological dynamics version of the Furstenberg correspondence principle, that connects Ramsey theory to topological dynamics. More precisely, we consider the following results:

Theorem 10 (van der Waerden’s theorem) For any ${k,r \geq 1}$ there exists ${N \geq 1}$ such that whenever ${[N]}$ is partitioned into colour classes ${[N] = E_1 \cup \ldots \cup E_r}$ , one of the colour classes ${E_i}$ contains an arithmetic progression ${a, a+n, \ldots, a+(k-1)n}$ of length ${k}$ with some ${n>0}$ .

Theorem 11 (Topological multiple recurrence) Let ${X}$ be a non-empty compact topological space, and let ${T: X \rightarrow X}$ be a homeomorphism. Then for any open cover ${X = U_1 \cup \ldots \cup U_r}$ of ${X}$ and any ${k \geq 1}$ , there exists an open set ${U_i}$ in this cover, a point ${x \in X}$ , and a positive integer ${n}$ such that ${x, T^n x, \ldots, T^{(k-1)n} x \in U_i}$ .

It is not difficult to use Theorem 10 to establish Theorem 11. Conversely, we will use ultraproducts to show that Theorem 11 implies Theorem 10. (We will not prove either of these theorems here, but see e.g. this previous blog post for a proof.)

Again, we use compactness and contradiction. Suppose for contradiction that Theorem 10 failed. Then there exists ${k,r \geq 1}$ such that for any standard ${{\bf n}}$ , we may partition ${[{\bf n}]}$ into colour classes ${[{\bf n}] = E_{1,{\bf n}} \cup \ldots E_{r,{\bf n}}}$ , none of which contain any ${k}$ -term arithmetic progressions. Taking ultraproducts, we obtain a partition ${[N] = E_1 \cup \ldots E_r}$ of the nonstandard interval ${[N]}$ associated to the unbounded natural number ${N := \lim_{{\bf n} \rightarrow \alpha} {\bf n}}$ into internal colour classes ${E_1,\ldots,E_r}$ , none of which contains a nonstandard ${k}$ -term arithmetic progression.

Now consider the shifted colour classes ${E_i + n \cap [N]}$ for ${n \in {\bf Z}}$ and ${i=1,\ldots,r}$ . These are a countable family of internal sets that cover ${[N]}$ , and so by countable saturation, this gives ${[N]}$ the structure of a compact topological space.

We would like to use the shift map ${T: x \mapsto x+1}$ on ${[N]}$ . Unfortunately, this map is not quite a bijection on ${[N]}$ . To get around this, we work in the slightly smaller space

$\displaystyle X := \bigcap_{n \in {\bf N}} [n, N-n].$

A further application of countable saturation reveals that ${X}$ is still compact (with the induced topology from ${[N]}$ ). Furthermore, the shift map ${T: x \mapsto x+1}$ can be verified to be a homeomorphism on ${X}$ , and as ${N}$ is unbounded, we see from the overspill principle that ${X}$ is non-empty. It is covered by the open sets ${E_i \cap X}$ , so by Theorem 11, we can find ${x \in X}$ and a (standard) positive integer ${n}$ such that ${x, x+n, \ldots, x+(k-1)n}$ lie in a single ${E_i \cap X}$ , thus ${E_i}$ contains a non-standard ${k}$ -term arithmetic progression, giving the required contradiction.

— 4. Algebraic geometry and ultraproducts —

Another use of ultraproducts is to provide a bridge between quantitative algebraic geometry and qualitative algebraic geometry. This topic is discussed in detail in this previous post; we will just give some key results here without proof.

Theorem 12 (Algebraic geometry is continuous with respect to ultralimits) Let ${k_{\bf n}}$ be a sequence of algebraically closed fields, let ${d \geq 0}$ be a natural number, and let ${V_{\bf n} \subset k_{\bf n}^d}$ be a (standard) affine algebraic set, that is to say the solution set of some finite number of polynomials ${P_{1,{\bf n}}, \ldots, P_{M,{\bf n}}: k_{\bf n}^d \rightarrow k_{\bf n}}$ . We define the complexity of an algebraic set ${V}$ to be the least ${M}$ such that ${V}$ is cut out by at most ${M}$ polynomials, each of degree at most ${M}$ .

Then the nonstandard set ${V_\alpha := \prod_{{\bf n} \rightarrow \alpha} V_{\bf n}}$ is an algebraic set if and only if the complexity of the ${V_{\bf n}}$ are uniformly bounded for ${{\bf n}}$ sufficiently close to ${\alpha}$ . Furthermore, if ${V_\alpha}$ is indeed an algebraic set, then:

(Continuity of dimension) The dimension of ${V_\alpha}$ is equal to the dimension of ${V_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ .

(Continuity of irreducibility) ${V_\alpha}$ is irreducible if and only if ${V_{\bf n}}$ is irreducible for ${{\bf n}}$ sufficiently close to ${\alpha}$ .

(Continuity of degree) The degree of ${V_\alpha}$ is equal to the degree of ${V_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ .

A similar statement holds for constructive sets: an ultraproduct ${E_\alpha = \prod_{{\bf n} \rightarrow \alpha} E_{\bf n}}$ of constructive sets ${E_{\bf n}}$ is constructive if and only if the original sets have uniformly bounded complexity for ${{\bf n}}$ sufficiently close to ${\alpha}$ . These claims are proven in the previous blog post; the basic idea is to express basic concepts such as dimension, irreducibility, and degree in first-order terms, so that Łos’s theorem may be applied.

Using this theorem and the compactness and contradiction method, one can easily convert a number of qualitative algebraic results into quantitative ones. For instance, it is a basic fact in qualitative algebraic geometry that every algebraic set decomposes into a finite number of irreducible sets. Using the above theorem (and a relationship between degree and complexity), one can then show that the number of such sets is bounded by a quantity depending only on the degree of the original set (and in particular, uniform in the choice of field); again, see the previous blog post for details. Such quantitative bounds can be obtained by other means (for instance, by using the machinery of schemes), but the ultrafilter approach, being so general in nature, requires almost no actual algebraic geometry to set up and use.

— 5. Metric completion and Gromov-Hausdorff limits —

We previously gave an analogy between ultraproducts and metric completion. It turns out that this analogy can be made substantially more precise. We first need some basic nonstandard analysis notation. Call a nonstandard real number ${x \in {}^* {\bf R}}$ bounded if one has ${|x| \leq C}$ for some standard ${C>0}$ , and infinitesimal if one has ${|x| \leq c}$ for all standard ${c>0}$ . For instance, if ${N}$ is an unbounded natural number, then ${1+\frac{1}{N}}$ is bounded (but not standard), and ${\frac{1}{N}}$ is infinitesimal. We write ${x=O(1)}$ and ${x=o(1)}$ to denote the assertions that ${x}$ is bounded and infinitesimal respectively.

Proposition 13 (Bolzano-Weierstrass theorem) If ${x}$ is a bounded nonstandard real, then there exists a unique standard real ${\hbox{st}(x)}$ , called the standard part of ${x}$ , such that ${x = \hbox{st}(x) + o(1)}$ , i.e. ${x - \hbox{st}(x)}$ is infinitesimal.

Proof: Uniqueness is clear (as no non-zero standard real can be infinitesimal). For existence, we consider the “Dedekind cut” ${\{ y \in {\bf R}: y < x \}}$ , which is a non-empty bounded half-line in ${{\bf R}}$ . Taking ${\hbox{st}(x)}$ to be the supremum of this cut, we easily verify that ${\hbox{st}(x)-\epsilon \leq x \leq \hbox{st}(x)+\epsilon}$ for any standard ${\epsilon > 0}$ , and the claim follows. $\Box$

One can also prove this theorem by the usual Bolzano-Weierstrass argument, trapping ${x}$ in a nested sequence of dyadic standard intervals; we leave this argument to the interested reader.

One can view the standard part operation ${\hbox{st}: O({\bf R}) \rightarrow {\bf R}}$ algebraically, as a homomorphism from the bounded nonstandard reals ${O({\bf R}) := \{ x \in {}^* {\bf R}: x = O(1) \}}$ to the standard reals with kernel ${o({\bf R}) := \{ x \in {}^* {\bf R}: x = o(1)\}}$ ; note that the sets ${O({\bf R}), o({\bf R})}$ are perfectly well-defined as an (external) set in the nonstandard analysis formalism, even though it does not quite make rigorous set-theoretic sense in finitary mathematics (one cannot use finitary asymptotic notation such as ${O()}$ inside set-builder notation). Thus for instance we can say that ${o({\bf R})}$ is an ideal in the ring ${O({\bf R})}$ , which is an assertion which is intuitively obvious in the finitary setting, but a bit hard to formalise properly. Note that ${{\bf R}}$ can then be interpreted as the image under the standard part map of the bounded nonstandard rationals ${O({\bf Q})}$ . This can in fact be used to give an alternative definition of the real numbers, which is the nonstandard version of the Cauchy completion construction; we leave this construction to the reader.

We can perform similar constructions with other metric spaces. Actually, in order to have a reaonable notion of boundedness, it is convenient to work in the category of pointed metric spaces ${(X,x_0) = (X,d,x_0)}$ , that is to say a metric space ${(X,d)}$ with a preferred “origin” ${x_0 \in X}$ . If one has a sequence ${(X_{\bf n}, d_{\bf n}, x_{0,{\bf n}})}$ of standard pointed metric spaces, one can take ultralimits and create a nonstandard pointed metric space ${(X_\alpha, d_\alpha, x_{0,\alpha})}$ . Here, ${X_\alpha := \prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ is the ultraproduct of the ${X_{\bf n}}$ , ${x_{0,\alpha} := \lim_{{\bf n} \rightarrow \alpha} x_{0,{\bf n}}}$ is a point in ${X_\alpha}$ , and ${d_\alpha: X_\alpha \times X_\alpha \rightarrow {}^* [0,+\infty)}$ is the ultralimit of the ${d_{\bf n}}$ .

At present, ${(X_\alpha,d_\alpha)}$ is a nonstandard metric space, but not an external metric space, because the nonstandard distance ${d_\alpha(x,y)}$ between two points in ${X_\alpha}$ is a nonstandard real, and not necessarily a bounded one. To create an external metric space, we cut down the size of ${X_\alpha}$ in two different ways. Firstly, we restrict attention to the bounded portion ${O(X_\alpha) := \{ x \in X_\alpha: d_\alpha(x,x_{0,\alpha}) = O(1) \}}$ of ${X_\alpha}$ . Next, we place an equivalence relation ${\sim}$ on ${O(X_\alpha)}$ by declaring ${x \sim y}$ if ${d_\alpha(x,y) = o(1)}$ . The quotient space ${O(X_\alpha)/\sim}$ , which we will denote suggestively as ${O(X_\alpha)/o(X_\alpha)}$ can then be checked to be a metric space with metric given by the formula

$\displaystyle d( [x], [y] ) := \hbox{st}( d_\alpha(x,y) )$

whenever ${x,y \in O(X_\alpha)}$ , with corresponding equivalence classes ${[x],[y] \in O(X_\alpha)/o(X_\alpha)}$ . The quotient map ${\hbox{st}: O(X_\alpha) \rightarrow O(X_\alpha)/o(X_\alpha)}$ will be called the standard part map, as it generalises the map in Proposition 13.

We refer to the pointed external metric spaces ${(O(X_\alpha)/o(x_\alpha), x_{0,\alpha})}$ as the nonstandard hull of the standard pointed metric spaces ${(X_{\bf n}, x_{0,{\bf n}})}$ ; it is also known as the ultralimit of these spaces, although we avoid this terminology here as we are using the term “ultralimit” for a slightly different (although certainly related) operation. These spaces are automatically complete, as can easily be verified using countable saturation. If the spaces ${X_{\bf n}}$ are asymptotically uniformly locally totally bounded in the sense that for every ${R,r>0}$ there exists ${M>0}$ such that for ${{\bf n}}$ sufficiently close to ${\alpha}$ , one can cover the balls ${B(x_{0,{\bf n}}, R)}$ by at most ${M}$ balls of radius ${r}$ , then the nonstandard hull ${O(X_\alpha)/o(x_\alpha)}$ is also locally totally bounded by Łos’s theorem, and thus locally compact by the Heine-Borel theorem. Furthermore, it is not difficult to show in this case that the ${(X_{\bf n}, x_{0,{\bf n}})}$ converge along ${\alpha}$ to ${(X_\alpha, x_{0,\alpha})}$ in the pointed Gromov-Hausdorff sense, thus for every ${R, \epsilon > 0}$ , the Gromov-Hausdorff distance between ${B(x_{0,{\bf n}}, R)}$ and ${B(x_{0,{\alpha}}, R)}$ is less than ${\epsilon}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ . In particular, this demonstrates the basic fact that any sequence of asymptotically uniformly locally totally bounded pointed metric spaces has a convergent subsequence in the pointed Gromov-Hausdorff sense.

There are several interesting special cases of the nonstandard hull construction. For instance, if the spaces ${X_{\bf n} = X}$ are equal to a single locally totally bounded space, then the nonstandard hull becomes a metric completion ${\overline{X}}$ of ${X}$ , with every bounded sequence ${x_{\bf n}}$ in ${X}$ giving rise to a limit point ${\hbox{st}( \lim_{{\bf n} \rightarrow \alpha} x_{\bf n})}$ in ${\overline{X}}$ . When the metric spaces are normed vector spaces, in which nonstandard analysis can be used as a framework to describe the theory of concentration compactness; see this previous blog post for further discussion. Finally, if one starts with a finitely generated group ${G}$ with a word metric ${d}$ , then by taking the nonstandard hull of ${G}$ with a rescaled word metric ${\frac{1}{R_{\bf n}} d}$ for a well-chosen set of radii ${R_{\bf n}}$ , one can obtain a useful metric space known as the asymptotic cone of ${G}$ , which for instance can be used to establish Gromov’s theorem on groups of polynomial growth; see this paper of van den Dries and Wilkie for details. Related to this, one can take the non-standard hull of a sequence of approximate groups (and the groups generated by such approximate groups) to obtain open neighbourhoods of locally compact groups, allowing one to use the theory of Hilbert’s fifth problem (which classifies the latter) to study approximate groups; see this text of mine for more discussion.

— 6. Loeb measure and regularity —

Measure theory, with its emphasis on countable additivity, is not obviously a first-order theory, and so it is not a priori obvious that it interacts well with ultraproducts. Nevertheless, thanks primarily to the countable saturation property of ultraproducts, one can often obtain a good notion of measure on nonstandard spaces, by carefully taking the ultralimit of measures on standard spaces. We give a fundamental such construction here, namely the Loeb measure construction, although for simplicity we restrict attention to the setting of nonstandard finite sets (also known as hyperfinite sets) to avoid some technicalities. Loeb measures are a special case of the more general concept of a Kiesler measure in model theory, but we will not discuss this more general concept here.

Let ${X_{\bf n}}$ be a sequence of standard non-empty finite sets, so that the ultraproduct ${X_\alpha = \prod_{{\bf n} \rightarrow \alpha} X_{\bf n}}$ is a nonstandard non-empty finite set. On each of the ${X_{\bf n}}$ , we can define the uniform probability measure ${\mu_{\bf n}}$ , which assigns the measure ${\mu_{\bf n}(E_{\bf n}) := \frac{|E_{\bf n}|}{|X_{\bf n}|}}$ to each subset ${E_{\bf n}}$ of ${X_{\bf n}}$ . Of course, ${\mu_{\bf n}}$ is a finitely additive probability measure. Taking ultraproducts and then taking standard parts, we can then define a finitely additive probability measure ${\mu_\alpha^0}$ on the boolean algebra ${{\cal B}_{X_\alpha}}$ of internal subsets ${E_\alpha = \prod_{{\bf n} \rightarrow \alpha} E_{\bf n}}$ of ${X_\alpha}$ , by the formula

$\displaystyle \mu_\alpha^0( \prod_{{\bf n} \rightarrow \alpha} E_{\bf n} ) := \hbox{st}( \lim_{{\bf n} \rightarrow \alpha} \mu_{\bf n}( E_{\bf n} ) ).$

One easily verifies that this is a finitely additive probability measure. Furthermore, thanks to the countable saturation property, we see that ${\mu_\alpha^0}$ is a premeasure, that is to say that one has the countable additivity property

$\displaystyle \mu_\alpha^0( \bigcup_{m=1}^\infty E_m ) = \sum_{m=1}^\infty \mu_\alpha^0( E_m )$

whenever ${E_1,E_2,\ldots}$ are a family of disjoint internal subsets of ${X_\alpha}$ whose union is also an internal subset. Applying the Caratheodory extension theorem (or more precisely, the Hahn-Kolmogorov theorem), we can then extend ${\mu_\alpha^0}$ to a countably additive probability measure ${\mu_\alpha}$ on the ${\sigma}$ -algebra ${{\cal L}_{X_\alpha}}$ generated by ${{\cal B}_{X_\alpha}}$ ; we refer to ${(X_\alpha, {\cal L}_{X_\alpha}, \mu_\alpha)}$ as a Loeb space, with ${\mu_\alpha}$ being the Loeb probability measure and ${{\cal L}_{X_\alpha}}$ being the Loeb ${\sigma}$ -algebra.

Remark 2 One technical caveat: in general, the Loeb ${\sigma}$ -algebra will not be countably generated, and so in particular the Lebesgue spaces ${L^p(X_\alpha, {\cal L}_{X_{\alpha}},\mu_\alpha)}$ associated to Loeb spaces will not be separable. However, in most finitary applications, one can often work with countably generated sub- ${\sigma}$ -algebras of the Loeb ${\sigma}$ -algebra, in which case separability can be restored.

The relationship between ${\mu_\alpha^0}$ and ${\mu_\alpha}$ is closely analogous to that between the elementary measure (or Jordan measure) of elementary subsets of (say) the unit cube, and that of Lebesgue measure of Borel subsets of that cube; see e.g. this text of mine for the basic theory here. For instance, it is not difficult to show that every Loeb measurable set ${F \subset X_\alpha}$ is “almost internal” in the sense that for any standard ${\epsilon > 0}$ , one can find an internal set ${E \subset X_\alpha}$ which is ${\epsilon}$ -close to ${F}$ in the sense that the outer measure

$\displaystyle \mu_\alpha^*(E \Delta F) := \inf \{ \sum_m \mu_\alpha^0(E_m): E_m \hbox{ internal and cover } E \Delta F \}$

of the symmetric difference ${E \Delta F}$ is at most ${\epsilon}$ . Related to this, the Loeb measure and the outer measure agree on any Loeb measurable set, and the simple internal functions on ${X_\alpha}$ (i.e. finite linear combinations of indicator functions of internal sets) will be dense in ${L^p( X_\alpha, {\cal L}_{X_\alpha}, \mu_{X_\alpha} )}$ for any (standard) ${1 \leq p < \infty}$ .

For instance, if ${N}$ is an unbounded natural number, then the set ${[o(N)] := \{ n \in [N]: n = o(N) \}}$ is not an internal subset of ${[N]}$ , but it is the intersection of the countable family ${[N/k] = \{ n \in [N]: n \leq N/k\}}$ of internal sets for ${k \in {\bf N}}$ . Each of the internal sets ${[N/k]}$ has measure ${\mu_{[N]}^0([N/k]) = \frac{1}{k}}$ , and so ${[o(N)]}$ is a Loeb measurable set with Loeb measure zero. As another example, for any standard ${q \geq 1}$ and ${a \in {\bf Z}/q{\bf Z}}$ , the residue class ${\{ n \in [N]: n = a\hbox{ mod } q \}}$ is an internal subset of ${[N]}$ of Loeb measure exactly ${1/q}$ (regardless of what the remainder of ${N}$ is modulo ${q}$ ).

As a quick application of Loeb measure, we give an instance of the Furstenberg correspondence principle, closely analogous to the topological dynamics example from a few sections earlier. Specifically, we connect the following two theorems:

Theorem 14 (Szemeredi’s theorem) For any ${k \geq 1}$ and ${\delta>0}$ there exists ${N \geq 1}$ such that whenever ${E \subset [N]}$ has density ${|E|/N}$ at least ${\delta}$ , ${E}$ contains an arithmetic progression ${a, a+n, \ldots, a+(k-1)n}$ of length ${k}$ with some ${n>0}$ .

Theorem 15 (Furstenberg multiple recurrence) Let ${(X, {\cal X}, \mu)}$ be a probability space, and let ${T: X \rightarrow X}$ be an almost everywhere defined bijection that is measure-preserving. Then for any set ${A \subset X}$ of positive measure and any ${k \geq 1}$ , there exists a point ${x \in X}$ , and a positive integer ${n}$ such that ${x, T^n x, \ldots, T^{(k-1)n} x \in A}$ .

Again, it is not difficult to show that Theorem 14 implies Theorem 15. To show the converse, we again use the compactness and contradiction method. If Theorem 14 failed, then there exist ${k \geq 1}$ and ${\delta>0}$ , and a sequence ${N_{\bf n}}$ going to infinity, together with subsets ${E_{\bf n} \subset [N_{\bf n}]}$ of density at least ${\delta}$ which contain no ${k}$ -term arithmetic progressions. Taking ultralimits, we obtain an unbounded natural number ${N}$ and an internal subset ${E \subset [N]}$ of Loeb measure at least ${\delta}$ which contains no non-standard ${k}$ -term arithmetic progressions. The shift map ${T: x \mapsto x+1}$ is defined and bijective almost everywhere on ${[N]}$ , and is measure-preserving, and Theorem 15 then provides the required contradiction. (As remarked earlier, this probability space is likely to be inseparable, but one can make it separable simply by reducing ${{\cal X}}$ to the ${\sigma}$ -algebra generated by ${E}$ and its (standard) shifts ${E+n}$ .)

Remark 3 The ultralimit construction actually gives a lot more relevant structure on ${[N]}$ than just that of a measure-preserving system. For instance, one can view the space ${\{ (x,x+h,x+k,x+h+k): x,x+h,x+k,x+h+k \in [N] \}}$ of parallelograms as a special subset of ${[N]^4}$ , which one can also endow with a Loeb measure, and these spaces (as well as higher-dimensional analogues) which can be used to analyse the further additive structure of ${[N]}$ (in a manner that closely parallels the structural theory of Host and Kra on measure-preserving systems); see this paper of Szegedy for some details of this approach.

The above example already shows the power of basic measure-theoretic tools (such as the Hahn-Kolmogorov theorem) in connecting discrete and continuous results together. Now we turn to some applications of other basic measure theory tools, such as product measure and conditional expectation. Specifically, we will use ultraproducts and measure theory to prove the following “strong” form of the Szemerédi regularity lemma:

Lemma 16 (Szemerédi regularity lemma) Let ${\epsilon>0}$ and ${F: {\bf N} \rightarrow {\bf N}}$ be a function. Then there exists ${C>1}$ with the following property: whenever ${V}$ is a finite non-empty set and ${f: V \times V \rightarrow [0,1]}$ is a function, there exists ${1 \leq M \leq C}$ and a decomposition

$\displaystyle f = f_{str} + f_{err} + f_{psd}$

where

(Structure) ${f_{str}}$ takes values in ${[0,1]}$ , and there exists a partition ${V = V_1 \cup \ldots \cup V_M}$ such that ${f_{str}}$ is constant on ${V_i \times V_j}$ for all ${1 \leq i,j \leq M}$ .

(Smallness) ${f_{err}}$ takes values in ${[-1,1]}$ , and ${{\bf E}_{v,w \in V} |f_{err}(v,w)|^2 \leq \epsilon}$ .

(Pseudorandomness) For any ${A,B \subset V}$ , one has ${|{\bf E}_{v,w \in V} 1_A(v) 1_B(w) f_{psd}(v,w)| \leq \frac{1}{F(M)}}$ .

The connection between the regularity lemma and nonstandard measure theory was first obtained by Elek and Szegedy, in which the extension of the arguments here to hypergraphs was also obtained.

We will deduce Lemma 16 from the following infinitary version:

Lemma 17 (Infinitary regularity lemma) Let ${\epsilon>0}$ be standard, and let ${V}$ be a nonstandard finite non-empty set. If ${f: V \times V \rightarrow [0,1]}$ is a Loeb measurable function on ${V \times V}$ , then there exists a decomposition

$\displaystyle f = f_{str} + f_{err} + f_{psd}$

where

(Structure) ${f_{str}}$ takes values in ${[0,1]}$ , and there exists a partition ${V = V_1 \cup \ldots \cup V_M}$ into finitely many internal sets such that ${f_{str}}$ is constant on ${V_i \times V_j}$ for all ${1 \leq i,j \leq M}$ .

(Smallness) ${f_{err}}$ takes values in ${[-1,1]}$ , and ${\int_{V \times V} |f_{err}(v,w)|^2\ d\mu_{V \times V}(v,w) < \epsilon}$ .

(Pseudorandomness) For any measurable ${A,B \subset V}$ , one has ${\int_{V \times V} 1_A(v) 1_B(w) f_{psd}(v,w)\ d\mu_{V \times V}(v,w) = 0}$ .

We will prove Lemma 17 shortly, but let us first see how it implies Lemma 16. We once again use the compactness and contradiction method. If Lemma 16 fails, then there exists ${\epsilon>0}$ and ${F: {\bf N} \rightarrow {\bf N}}$ , and for each ${{\bf n}}$ there exists a finite non-empty set ${V_{\bf n}}$ and a function ${f_{\bf n}: V_{\bf n} \times V_{\bf n} \rightarrow [0,1]}$ , such that for no ${1 \leq M \leq {\bf n}}$ does there exist a decomposition

$\displaystyle f_{\bf n} = f_{str,{\bf n}} + f_{err,{\bf n}} + f_{psd,{\bf n}}$

obeying the conclusions of Lemma 16. We then take ultralimits to obtain a nonstandard finite non-empty set ${V_\alpha}$ and an internal function ${f_\alpha: V_\alpha \times V_\alpha \rightarrow {}^* [0,1]}$ . The standard part ${f := \hbox{st} f_\alpha}$ is then a Loeb measurable function on ${V \times V}$ taking values in ${[0,1]}$ . We apply Lemma 17 to obtain a decomposition

$\displaystyle f = f_{str} + f_{err} + f_{psd}$

with the stated properties for some finite ${M}$ . Note that ${f_{str}}$ is already a simple internal function. The function ${f_{psd}}$ need not be simple internal, but may be approximated to arbitrary accuracy in ${L^2(V \times V, {\cal L}_{V \times V}, \mu_{V \times V})}$ by a simple internal function. Thus we may find a decomposition

$\displaystyle f_\alpha = f_{str} + f'_{err} + f'_{psd}$

where ${f'_{psd}}$ is simple internal and is such that

$\displaystyle |\int_{V \times V} 1_A(v) 1_B(w) f'_{psd}(v,w)\ d\mu_{V \times V}(v,w)| < \frac{1}{F(M)}$

for all measurable ${A,B \subset V}$ , and ${f'_{err}}$ is simple internal, takes values in ${[-1,1]}$ , and is such that

$\displaystyle \int_{V \times V} |f'_{err}(v,w)|^2\ d\mu_{V \times V}(v,w) < \epsilon.$

By Łos’s theorem, an analogous decomposition then holds for ${f_{\bf n}}$ for ${{\bf n}}$ sufficiently close to ${\alpha}$ , but this contradicts the construction of the ${f_{\bf n}}$ .

Now we prove Lemma 17. The proof hinges on a comparison between two spaces, the Loeb space

$\displaystyle (V \times V, {\cal L}_{V \times V}, \mu_{V \times V})$

on the product space ${V \times V}$ , and the subtly different probability space

$\displaystyle (V \times V, {\cal L}_V \times {\cal L}_V, \mu_V \times \mu_V)$

that is the product of the Loeb space ${(V, {\cal L}_V, \mu_V)}$ with itself, thus ${{\cal L}_V \times {\cal L}_V}$ is the ${\sigma}$ -algebra on ${V \times V}$ generated by rectangles ${A \times B}$ with ${A,B}$ Loeb measurable in ${V}$ , and ${\mu_V \times \mu_V}$ is the product measure, which is the unique probability measure on ${{\cal L}_V \times {\cal L}_V}$ such that

$\displaystyle \mu_V \times \mu_V(A \times B) = \mu_V(A) \mu_V(B)$

for all Loeb measurable ${A,B \subset V}$ .

It is not difficult to show that the former probability space is a refinement of the latter, thus ${{\cal L}_{V \times V}}$ contains ${{\cal L}_V \times {\cal L}_V}$ , and ${\mu_{V \times V}}$ and ${\mu_V \times \mu_V}$ agree on their common domain ${{\cal L}_V \times {\cal L}_V}$ of definition. However, the former space is larger in general; the basic reason for this is for large finite spaces ${V_{\bf n}}$ , it is possible to find subsets of ${V_{\bf n} \times V_{\bf n}}$ that are not well approximable by bounded boolean combinations of rectangles ${A_{\bf n} \times B_{\bf n}}$ (e.g. random subsets of ${V_{\bf n} \times V_{\bf n}}$ will have this property with high probability in the asymptotic limit when ${|V_{\bf n}|}$ goes to infinity). Despite this disparity, we may still form the conditional expectation ${\mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V )}$ of ${f}$ , which one can define as the orthogonal projection of ${f}$ in the Hilbert space ${L^2( V \times V, {\cal L}_{V \times V}, \mu_{V \times V})}$ to the closed subspace ${L^2( V \times V, {\cal L}_V \times {\cal L}_V, \mu_V \times \mu_V )}$ . We then have a decomposition

$\displaystyle f = \mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V ) + f_{psd}$

where ${f_{psd}}$ is orthogonal to all ${{\cal L}_V \times {\cal L}_V}$ -measurable functions; in particular, it is orthogonal to ${1_{A \times B}}$ for any Loeb measurable ${A,B \subset V}$ , so that

$\displaystyle \int_{V \times V} 1_A(v) 1_B(w) f_{psd}(v,w)\ d\mu_{V \times V}(v,w) = 0$

for all such ${A,B}$ .

Next, we know that ${{\cal L}_V \times {\cal L}_V}$ is generated (up to null sets) by products ${A \times B}$ of internal sets, so we may approximate ${\mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V )}$ to arbitary error in ${L^2}$ by a simple function ${f_{str}}$ that is a finite linear combination of indicators ${1_{A \times B}}$ of rectangles; as ${f}$ takes values in ${[0,1]}$ , we can ensure that ${\mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V )}$ and ${f_{str}}$ . This gives a decomposition

$\displaystyle \mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V ) = f_{str} + f_{err}$

and one easily verifies that all the required properties of Lemma 17 are obeyed.

Remark 4 It is instructive to deconstruct this proof and compare it with the standard “energy increment” proof of the regularity lemma. The energy increment process is now concealed within the standard proof of the existence of orthogonal projections in Hilbert spaces (see e.g. Proposition 1 of this previous blog post), so on some level the two proofs of the regularity lemma are essentially equivalent. However, the ultrafilter proof allows one to hide many of the ingredients of the argument into existing Hilbert space theory.

Remark 5 A similar construction allows one to extract a graph limit from a sequence of finite graphs ${f_{\bf n}: V_{\bf n} \times V_{\bf n} \rightarrow [0,1]}$ , by first forming the ultraproduct ${f: V \times V \rightarrow [0,1]}$ and then the conditional expectation ${\mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V )}$ , which is an ${{\cal L}_V \times {\cal L}_V}$ -measurable function from ${V \times V}$ to ${[0,1]}$ . At this point we encounter the technical issue noted previously that ${{\cal L}_V}$ is not countably generated. However, we may find a countably generated sub- ${\sigma}$ -algebra ${{\cal V}}$ of ${{\cal L}_V}$ with the property that ${\mathop{\bf E}( f | {\cal L}_V \times {\cal L}_V )}$ is equal ${\mu_{V \times V}}$ -almost everywhere with a ${{\cal V} \times {\cal V}}$ -measurable function ${f_\infty: V \times V \rightarrow [0,1]}$ , by expressing ${f}$ as the almost everywhere limit of simple functions (bounded linear combinations of rectangles ${1_{A \times B}}$ with ${A,B \in {\cal L}_V}$ ) and then letting ${{\cal V}}$ be the ${\sigma}$ -algebra generated by the ${A,B}$ . The function ${f_\infty}$ is then essentially a graphon, after lifting the separable probability space ${(V, {\cal L}_V, \mu_V)}$ to the unit interval with uniform Lebesgue measure in the standard fashion. Among other things, this construction can give an alternate proof that every sequence of graphs has a subsequence converging to a graphon.

Remark 6 Although it is not needed here, one convenient fact about Loeb spaces on products is that they obey the following Fubini-Tonelli type theorem: if ${V, W}$ are nonstandard finite spaces and ${f: V \times W \rightarrow [0,+\infty]}$ is Loeb measurable on ${V \times W}$ , then for all ${v \in V}$ , the function ${w \mapsto f(v,w)}$ is Loeb measurable on ${W}$ , the integral ${v \mapsto \int_W f(v,w)\ d\mu_W(w)}$ is Loeb measurable on ${V}$ , and we have the identity

$\displaystyle \int_{V \times W} f(v,w)\ d\mu_{V \times W}(v,w) = \int_V ( \int_W f(v,w)\ d\mu_W(w) )\ d\mu_V(v).$

Similarly if the roles of ${V}$ and ${W}$ are swapped; in particular we have the familiar identity

$\displaystyle \int_V ( \int_W f(v,w)\ d\mu_W(w) )\ d\mu_V(v) = \int_W ( \int_V f(v,w)\ d\mu_V(v) )\ d\mu_W(w).$

These identities are obvious when ${f}$ is an internal simple function (as it follows from the corresponding claim in the finite case), and the general case follows from a standard approximation argument (using the monotone convergence theorem repeatedly). One can also obtain an analogous claim in the absolutely integrable category, in the spirit of Fubini’s theorem; we leave this to the interested reader.

33 comments

Comments feed for this article

7 December, 2013 at 10:44 pm

Terrence Tao Blog: Bridging Discrete & Continuous Analysis | Math Online Tom Circle

[…] https://terrytao.wordpress.com/2013/12/07/ultraproducts-as-a-bridge-between-discrete-and-continuous-a… […]

8 December, 2013 at 2:05 am

Victor Porton

Another approach to discrete mathematics is to use funcoids and reloid. A funcoid may represent both proximal space or a topological space, or a discrete object such as a graph. Such things as continuity are defined for funcoids, generalizing both continuous and discrete cases.
http://www.mathematics21.org/algebraic-general-topology.html

8 December, 2013 at 6:23 am

Pedantic note: “Los” should really be “Łoś”.

[Corrected, thanks – T.]

8 December, 2013 at 6:38 am

Alexander Shamov

In the discussion after Proposition 13 “bounded nonstandard integers $O(\mathbb{Q})$ ” should be “rationals”.

[Corrected, thanks – T.]

8 December, 2013 at 8:28 am

Bo Jacoby

Sorry for being off topic. I wish to know if this elementary result is really new? http://www.academia.edu/3247833/Statistical_induction_and_prediction

8 December, 2013 at 12:09 pm

Victor Porton

Limits to ultrafilters are somehow similar to my attempt to define a theory of generalized limits (in singularity points), but I consider filters rather than only ultrafilters. My attempt to construct in my way a theory in singularities is inhibited by some problems (some of which are precisely formulated and some are not), like these open problems.

9 December, 2013 at 1:51 am

Could this approach be useful in Graph theory problems such as Graph capaity http://en.wikipedia.org/wiki/Shannon_capacity_of_a_graph? When can solutions to semidefinite relaxations be thought of representing a property of a graph limit when the sequences of graphs are constructed in a particular way? Noga Alon with his student has show the capacity problem could be undecidable because the convergence property is true but the pace of convergence could have jumps. Can such difficult problems be studied with the technique at hand?

9 December, 2013 at 7:31 am

Boolean Algebra |

[…] Ultraproducts as a Bridge Between Discrete and Continuous … https://terrytao.wordpress.com/Some of the material here is drawn from previous blog posts, notably “Ultraproducts as a bridge between hard analysis and soft analysis” and “Ultralimit analysis and quantitative algebraic geometry“'. The text … Discrete analysis, of course, is primarily interested in the study of discrete (or “finitary”) mathematical objects: integers, rational numbers (which can be viewed as ratios of integers), finite sets, finite graphs, finite or discrete metric spaces, and so forth. However … […]

9 December, 2013 at 10:32 am

Ultraprodukte | UGroh's Weblog

[…] In der Vorlesung zur Funktionalanalysis hatte ich Ultrafilter als ein Möglichkeit angesprochen, kompakte topologische Räume zu definieren. Dass diese auf H. Cartan zurückgehende Definition auch für viele andere mathematische Fragestellung sinnvoll ist belegt der Artikel von T. Tao. […]

9 December, 2013 at 3:23 pm

Anonymous

Near the end of definition 3, “for every k-ary operation M” should be “for every k-ary operation O”

[Corrected, thanks – T.]

11 December, 2013 at 2:50 pm

Blake Stacey

Typo: “Gromov-Hausorff limits”

[Corrected, thanks – T.]

24 January, 2014 at 4:57 pm

Michelangelo

I don’t know if it can be useful, there are two articles on a similar topic by Bruno de Finetti: “La struttura delle distribuzioni in un insieme astratto qualsiasi” and “Sulla teoria astratta della misura e dell’integrazione”; english translations (“The structure of distributions on abstract spaces” and “On the abstract theory of measure and integration”) can be found in “Probability, Induction and Statistics: The art of guessing”, J. Wiley, N. Y., 1972.

5 May, 2014 at 3:36 pm

Hindman’s Theorem | Finite Playground

[…] reading the posts on ultrafilters by Terry Tao [1,2], I find the following result […]

5 June, 2014 at 9:56 am

When is correlation transitive? | What's new

[…] (i.e. in the formalism of inner product spaces) we will need a non-principal ultrafilter (see e.g this previous blog post for basic theory of ultrafilters); we leave it as an exercise to the reader to figure out how to […]

25 June, 2014 at 10:07 am

Lebesgue measure as the invariant factor of Loeb measure | What's new

[…] some basic familiarity with nonstandard analysis and ultraproducts, as covered for instance in this previous blog post.) Given an unbounded nonstandard natural number , one can define two external additive subgroups of […]

7 July, 2014 at 2:20 am

The subspace theorem approach to Siegel’s theorem on integral points on curves via nonstandard analysis | What's new

[…] out that finiteness theorems are very compatible with the language of nonstandard analysis. (See this previous blog post for a review of the basics of nonstandard analysis, and in particular for the nonstandard […]

12 October, 2014 at 11:57 am

Additive limits | What's new

[…] analysis (or of ultraproducts); see for instance this paper of Elek and Szegedy, Section 6 of this previous blog post, or this paper of Towsner. (In this post we assume some familiarity with nonstandard analysis, as […]

20 July, 2015 at 8:23 pm

A nonstandard analysis proof of Szemeredi’s theorem | What's new

[…] of a standard part of a bounded real number, and the Loeb measure construction), see for instance this previous blog post for a […]

20 July, 2015 at 10:52 pm

Lior Silberman

Correction: after Remark 1, in “One can also view [the ultralimit of a sequence in a finite set] as the outcome of an “election” among candidates in {X}, in which each “voter” $\mathbf{n}$ has $\mathbf{n}$ as a preferred candidate”, the second n should be $x_\mathbf{n}$ , I think.

[Corrected, thanks – T.]

16 September, 2015 at 7:09 pm

The One About .999… |

[…] than 1, you might at some point want to learn about the hyperreal number system, and the concept of ultralimits. In this context, .999… is less than 1, and for a very appealing reason: since each individual […]

5 March, 2016 at 10:11 am

Sean Eberhard

Dear Terry,

I’m trying to flesh out the details of Remark 5 here. Is it true for some reason that if $\Omega$ is a hyperfinite set and $\Sigma$ any separable sub- $\sigma$ -algebra of the Loeb $\sigma$ -algebra then $(\Omega,\Sigma,\mu)$ is a standard probability space (in the sense of https://en.wikipedia.org/wiki/Standard_probability_space)?

5 March, 2016 at 11:40 pm

Terence Tao

My guess would be that these spaces would not exactly be standard probability spaces, but ought to be equivalent modulo null sets to a standard probability space. If I recall correctly, there is some discussion of these issues in Furstenberg’s book, something along the lines that every separable probability space has a standard probability space model which is equivalent up to null sets. But I don’t have that book handy right now.

25 September, 2016 at 11:45 pm

Maths student

Dear Prof. Tao,

in remark 1, it seems as though “ultrafilters” must be replaced by “non-principal ultrafilters”, for the existence of ultrafilters is given by the principal ultrafilters.

[Corrected, thanks – T.]

28 September, 2016 at 2:31 am

Maths student

Dear Prof. Tao,

It seems as though in Definition 2 in the last line of the first paragraph (“We identify every standard object…”), the subscript from the limit has to be dropped, or one would set $x_n = x$ for all $n$ .

[Corrected, thanks – T.]

1 March, 2017 at 11:59 am

Special cases of Shannon entropy | What's new

[…] As before, every linear inequality or equality that is valid for the information-theoretic quantities discussed above, is automatically valid for the linear algebra counterparts for subspaces of a vector space over a finite field by applying the above specialisation (and dividing out by the normalising factor of ). In fact, the requirement that the field be finite can be removed by applying the compactness theorem from logic (or one of its relatives, such as Los’s theorem on ultraproducts, as done in this previous blog post). […]

2 September, 2017 at 8:39 pm

espressonator

Perhaps instead of “finite subspace”, you meant “finite dimensional subspace”?

[Corrected, thanks – T.]

14 July, 2018 at 3:05 pm

Fausto di Biase

It seems to me that the information encoded by a filter, say alfa, is given by the ”small” sets it contains. Indeed, if alfa contains a set A, it also necessarily contains the supersets of A, but it does not necessarily contain any given subset of A. So, I am not sure why you choose to call ”alfa-large” the members of alfa, rather than ”alfa-small”.

17 July, 2018 at 2:52 pm

Terence Tao

“Members of” is not the same as “information encoded by”. As you note, the larger the set is, the more likely it is to lie in the filter $\alpha$ , so it is natural to view sets in the filter as being large instead of small. For instance, in the cofinite filter, the only sets that lie in the filter are those that are so large that their complements are finite.

21 July, 2018 at 4:21 pm

Fausto di Biase

You are right. Thank you!

I guess what tricked me is the fact that if we pick a point $x$ ”at random” in the powerset of $\mathbb{N}$ (with the hope of getting elements of a given filter $\alpha$ of subsets of $\mathbb{N}$ ), and if we are lucky and end up finding that $x$ belongs to $\alpha$ , then the interesting thing to do, in order to find other elements of $\alpha$ , is to go ”downwards” and pick a subset of $x$ ”at random”, with the hope of finding another element of $\alpha$ (since the supersets of $x$ will be trivially be elements of $\alpha$ ).

I guess I had this in mind when I wrote that the ”information is given by the small sets”.

On the other hand, if we are unlucky and find out that $x$ is not an element of $\alpha$ , then the thing to do is to go ”upwards” and pick a superset of $x$ ”at random”, with the hope of finding an element of $\alpha$ , since no subset of $x$ will belong to $\alpha$ in this case. We could say that this $x$ is not ”large enough” to belong to $\alpha$ .

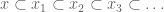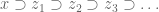A curious fact about the cofinite filter $\alpha$ is that, if $x$ belongs to it, and if we look for an ascending chain $x\subset x_1\subset x_2\subset x_3\subset\ldots$ of distinct elements of $\alpha$ starting from $x$ , then we will only find finite chains, while if we look for descending chains $x\supset z_1\supset z_2\supset z_3\supset\ldots$ of distinct elements of $ latex \alpha$ starting from $x$ , we will find infinite chains. There is no ”smallest” element in $\alpha$ contained in a given $x\in\alpha$ . Indeed, the intersection of all elements of $\alpha$ is empty.

Thank you for this beautiful post.

3 October, 2020 at 6:27 pm

porton

Terry,

Previously I have been written in this comment stream that I “attempt” to construct “noncontinuous” analysis (common generalization of continuous analysis and discrete analysis, as well as analysis of any arbitrary functions (having some topological structure)). I succeeded!!

I already defined (generalized) limit of an arbitrary (even discontinuous) function. Now I have written a text how to manipulate these limits (e.g. add or multiply them). I even defined what a noncontinuous solution of a differential equation means.

Need to say that it makes obvious to define derivatives and integrals (as well as infinite sums) for arbitrary functions?

Hm, probably my generalized limit is equivalent to the limit \union all the ultralimits on ultrafilters over the given filter (not checked the statement given in this paragraph yet). Quite an obvious idea, but nobody formulated it.

Here is the text about generalized limit:
https://mathematics21.org/limit-of-discontinuous-function/

Moreover, this generalized limit trivially generalizes further to limits on arbitrary “spaces”. I define the concept of “space” that encompasses all kinds of spaces in topology, including topological, proximity, uniform, metric spaces, locales and frames, etc. in this text:
https://mathematics21.org/the-algebra-of-general-topology/

Nominate me for Abel and Breakthrough prizes for these works! Seriously.

5 October, 2020 at 8:17 pm

Professor Van Nostrand

Dear Victor Porton,

I have just studied your work on algebraic general topology and I am nominating you for Abel prize.

Best of luck.
Van Nostrand

5 October, 2020 at 8:37 pm

porton

Prof. Van,

Your reply would be absolutely feasible, unless one reason:

You had too little time to really study several hundreds pages. So, what you say is definitely a silly joke.

BTW, here are short introductions:

Click to access present.pdf

Click to access intro.pdf

Oops, both those two introductions miss the discovery (probably, my main discovery) from
https://mathematics21.org/the-algebra-of-general-topology/

6 October, 2020 at 11:35 am

Anonymous

Self-promoting comments are not allowed in this blog.

	Yingyuan Li on Analysis II
	Anonymous on Analysis II
	Anonymous on Analysis II
	Yingyuan Li on Analysis II
	Yingyuan Li on Analysis II
	Yingyuan Li on Analysis II
	Yingyuan Li on Analysis II
	Jamie on On writing
	Anonymous on On writing
	Terence Tao on PCAST Working Group on Generat…
	Yingyuan Li on Analysis II
	Sam on 245A, Notes 5: Differentiation…
	Johan Aspegren on PCAST Working Group on Generat…
	Sam on 245A, Notes 5: Differentiation…
	wbshu on 247B, Notes 1: Restriction…

Ultraproducts as a Bridge Between Discrete and Continuous Analysis

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

33 comments

Leave a Reply Cancel reply

For commenters

Ultraproducts as a Bridge Between Discrete and Continuous Analysis

Share this:

Like this:

Recent Comments

Articles by others

Diversions

Mathematics

Selected articles

Software

The sciences

Top Posts

Archives

Categories

The Polymath Blog

33 comments

Leave a Reply Cancel reply

For commenters