I’ve just uploaded to the arXiv my paper “Outliers in the spectrum of iid matrices with bounded rank perturbations“, submitted to Probability Theory and Related Fields. This paper is concerned with outliers to the circular law for iid random matrices. Recall that if is an
matrix whose entries are iid complex random variables with mean zero and variance one, then the
complex eigenvalues of the normalised matrix
will almost surely be distributed according to the circular law distribution
in the limit
. (See these lecture notes for further discussion of this law.)
The circular law is also stable under bounded rank perturbations: if is a deterministic rank
matrix of polynomial size (i.e. of operator norm
), then the circular law also holds for
(this is proven in a paper of myself, Van Vu, and Manjunath Krisnhapur). In particular, the bulk of the eigenvalues (i.e.
of the
eigenvalues) will lie inside the unit disk
.
However, this leaves open the possibility for one or more outlier eigenvalues that lie significantly outside the unit disk; the arguments in the paper cited above give some upper bound on the number of such eigenvalues (of the form for some absolute constant
) but does not exclude them entirely. And indeed, numerical data shows that such outliers can exist for certain bounded rank perturbations.
In this paper, some results are given as to when outliers exist, and how they are distributed. The easiest case is of course when there is no bounded rank perturbation: . In that case, an old result of Bai and Yin and of Geman shows that the spectral radius of
is almost surely
, thus all eigenvalues will be contained in a
neighbourhood of the unit disk, and so there are no significant outliers. The proof is based on the moment method.
Now we consider a bounded rank perturbation which is nonzero, but which has a bounded operator norm:
. In this case, it turns out that the matrix
will have outliers if the deterministic component
has outliers. More specifically (and under the technical hypothesis that the entries of
have bounded fourth moment), if
is an eigenvalue of
with
, then (for
large enough),
will almost surely have an eigenvalue at
, and furthermore these will be the only outlier eigenvalues of
.
Thus, for instance, adding a bounded nilpotent low rank matrix to will not create any outliers, because the nilpotent matrix only has eigenvalues at zero. On the other hand, adding a bounded Hermitian low rank matrix will create outliers as soon as this matrix has an operator norm greater than
.
When I first thought about this problem (which was communicated to me by Larry Abbott), I believed that it was quite difficult, because I knew that the eigenvalues of non-Hermitian matrices were quite unstable with respect to general perturbations (as discussed in this previous blog post), and that there were no interlacing inequalities in this case to control bounded rank perturbations (as discussed in this post). However, as it turns out I had arrived at the wrong conclusion, especially in the exterior of the unit disk in which the resolvent is actually well controlled and so there is no pseudospectrum present to cause instability. This was pointed out to me by Alice Guionnet at an AIM workshop last week, after I had posed the above question during an open problems session. Furthermore, at the same workshop, Percy Deift emphasised the point that the basic determinantal identity
for matrices
and
matrices
was a particularly useful identity in random matrix theory, as it converted problems about large (
) matrices into problems about small (
) matrices, which was particularly convenient in the regime when
and
was fixed. (Percy was speaking in the context of invariant ensembles, but the point is in fact more general than this.)
From this, it turned out to be a relatively simple manner to transform what appeared to be an intractable matrix problem into quite a well-behaved
matrix problem for bounded
. Specifically, suppose that
had rank
, so that one can factor
for some (deterministic)
matrix
and
matrix
. To find an eigenvalue
of
, one has to solve the characteristic polynomial equation
This is an determinantal equation, which looks difficult to control analytically. But we can manipulate it using (1). If we make the assumption that
is outside the spectrum of
(which we can do as long as
is well away from the unit disk, as the unperturbed matrix
has no outliers), we can divide by
to arrive at
Now we apply the crucial identity (1) to rearrange this as
The crucial point is that this is now an equation involving only a determinant, rather than an
one, and is thus much easier to solve. The situation is particularly simple for rank one perturbations
in which case the eigenvalue equation is now just a scalar equation
that involves what is basically a single coefficient of the resolvent . (It is also an instructive exercise to derive this eigenvalue equation directly, rather than through (1).) There is by now a very well-developed theory for how to control such coefficients (particularly for
in the exterior of the unit disk, in which case such basic tools as Neumann series work just fine); in particular, one has precise enough control on these coefficients to obtain the result on outliers mentioned above.
The same method can handle some other bounded rank perturbations. One basic example comes from looking at iid matrices with a non-zero mean and variance
; this can be modeled by
where
is the unit vector
. Here, the bounded rank perturbation
has a large operator norm (equal to
), so the previous result does not directly apply. Nevertheless, the self-adjoint nature of the perturbation has a stabilising effect, and I was able to show that there is still only one outlier, and that it is at the expected location of
.
If one moves away from the case of self-adjoint perturbations, though, the situation changes. Let us now consider a matrix of the form , where
is a randomised version of
, e.g.
, where the
are iid Bernoulli signs; such models were proposed recently by Rajan and Abbott as a model for neural networks in which some nodes are excitatory (and give columns with positive mean) and some are inhibitory (leading to columns with negative mean). Despite the superficial similarity with the previous example, the outlier behaviour is now quite different. Instead of having one extremely large outlier (of size
) at an essentially deterministic location, we now have a number of eigenvalues of size
, scattered according to a random process. Indeed, (in the case when the entries of
were real and bounded) I was able to show that the outlier point process converged (in the sense of converging
-point correlation functions) to the zeroes of a random Laurent series
where are iid real Gaussians. This is basically because the coefficients of the resolvent
have a Neumann series whose coefficients enjoy a central limit theorem.
On the other hand, as already observed numerically (and rigorously, in the gaussian case) by Rajan and Abbott, if one projects such matrices to have row sum zero, then the outliers all disappear. This can be explained by another appeal to (1); this projection amounts to right-multiplying by the projection matrix
to the zero-sum vectors. But by (1), the non-zero eigenvalues of the resulting matrix
are the same as those for
. Since
annihilates
, we thus see that in this case the bounded rank perturbation plays no role, and the question reduces to obtaining a circular law with no outliers for
. As it turns out, this can be done by invoking the machinery of Van Vu and myself that we used to prove the circular law for various random matrix models.

18 comments
Comments feed for this article
23 December, 2010 at 2:16 pm
Djalil
Hi!
This reminds me this paper by Silverstein: http://www.ams.org/mathscinet-getitem?mr=1284550
About these matrices with iid entries, I wonder if one can prove the universality of the Gumbel fluctuation of the spectral radius (the result is known for the complex Ginibre ensemble).
23 December, 2010 at 5:30 pm
Terence Tao
Thanks for the reference, which I was not aware of! Silverstein’s paper does indeed much give the same control on the outlier eigenvalue of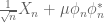 as my paper does (and indeed the methods are basically the same).
as my paper does (and indeed the methods are basically the same).
As for your second question, we don’t yet have enough fine-scale control on the circular law to come close to answering this sort of question yet – the behaviour in the boundary region , in particular, is still too delicate to resolve. (The results here avoid this because they only need one to understand the resolvent etc. in the region
, in particular, is still too delicate to resolve. (The results here avoid this because they only need one to understand the resolvent etc. in the region 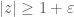 for some fixed
for some fixed 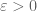 independent of
independent of  .)
.)
24 December, 2010 at 12:12 am
Djalil
There is also this paper by Andrew:
http://www.ams.org/mathscinet-getitem?mr=1062321
25 December, 2010 at 6:25 am
Timothy
Should be “This paper is concerned with”
[Corrected, thanks – T.]
26 December, 2010 at 12:52 pm
Terence Tao
I’ve deleted a number of comments on this post that involved (or were in response to) attempts at spoofing the identity of an author. Needless to say, such attempts are not welcome at this blog.
26 December, 2010 at 9:26 pm
Timothy
Shouldn’t it be “uploaded my paper.”
[Corrected, thanks. It’s been a while since I wrote a singly authored paper – T.]
29 December, 2010 at 5:33 am
Benaych-Georges
Shouldn’t it be “perturbation” instead of “permutation” in the title ?
By the way, the same technics were used to locate the outliers in the spectrums of either additive or multiplicative perturbations of rather general matrices in http://hal.archives-ouvertes.fr/hal-00423593/fr/
29 December, 2010 at 9:36 am
Terence Tao
Thanks for the correction and for the reference!
Best,
Terry
3 January, 2011 at 9:28 am
Raj Rao
In the paper:
Restricted rank modification of the symmetric eigenvalue problem: Theoretical considerations by Arbenz, Gander, Golub
the formula in your Remark 2.2 is referred to as the “modified Weinstein determinant” following Weinstein and Stenger’s “Methods for Intermediate Problems for Eigenvalues”.
Just FYI :-)
4 January, 2011 at 9:46 pm
Terence Tao
Thanks for the reference!
3 January, 2011 at 9:30 am
Raj Rao
(Or at least its analogue in the symmetric case)
16 January, 2011 at 10:47 pm
andrescaicedo
Terry, didn’t you have a post discussing identity (1)? Seems to have disappeared. (Maybe I’m confused?)
17 January, 2011 at 5:00 am
Terence Tao
I discussed this identity at
17 January, 2011 at 8:17 am
andrescaicedo
Thanks!
19 April, 2011 at 4:24 pm
Yashar
Hi Terry,
I have a question about the non-self-adjoint case that was studied by Rajan and Abbott. Simulations suggest that the total number of outlier eigenvalues (at least in the “balanced” case where the components of \psi_n sum up to 0) scales like \sqrt(n) (up to n ~ 3000). But you say above that the outlier point process converges to the zeros of that random Laurent series which is independent of n, suggesting that the number of outliers is O(1), and not O(\sqrt(n)), and my simulations are not actually showing the very large n behavior.
Am I right (in concluding the number is O(1) based on what you say), or am I missing something?
I would really appreciate your answer.
Thanks.
19 April, 2011 at 4:27 pm
Yashar
I guess I found my own mistake: the Laurent series has infinite zeros actually…
8 September, 2012 at 5:17 pm
Char
Hi Terry, I have a question about the distribution of the outliers. According to Silverstein’s paper, outliers are N~(mu*n,sigma^2) given that the outliers are not normalised. I ran a simulation with R. I tried different values of n, mu, sigma and roughly 1000 matrices. I got the mean of the outliers of mu*n but I got the standard deviation approximately sigma*sqrt(2) instead of sigma. Is it a correct result?
13 January, 2013 at 12:36 pm
Matrix identities as derivatives of determinant identities « What’s new
[…] for some . (This type of situation is also common in random matrix theory, for instance it arose in this previous paper of mine on outliers to the circular law.) If is invertible, then from (1) and (2) one […]